本文作者为张俊鹏、任启涵、张拳石,其中张俊鹏是张拳石老师的准入学博士生,任启涵是张拳石老师的博士生。
本文首先简单回顾了『等效交互可解释性理论体系』(20 篇 CCF-A 及 ICLR 论文),并在此基础上,严格推导并预测出神经网络在训练过程中其概念表征及其泛化性的动力学变化,即在某种程度上,我们可以解释在训练过程中神经网络在任意时间点的泛化性及其内在根因。
一、前言
长期以来,我们团队一直在思考可解释性领域的一个终极问题,即什么才是解释性领域的第一性原理?所谓第一性原理,目前没有一个被广泛接受的框架,世上本无路,我们需要逐渐去定义这样一个路。我们需要在一个新的理论体系中,提出大量的公理性要求,得出一个可以从不同的角度全方位精确严谨解释神经网络内在机理的理论。一套理论系统能严谨解释神经网络的方方面面才叫 “第一性原理”。
如果你真的在严谨地做 “科学”,那么第一性原理一定不是想象中简单,而是一个复杂的体系,需要研究照顾到深度学习中方方面面纷繁复杂的现象。当然,如果你主观上不愿意或者不信一个理论需要足够严谨,那么研究会变得简单千万倍。就像物理学的标准模型一定比牛顿定律复杂,取决于你希望走哪条路。
沿着这个方向,我们团队独立从头构建了『等效交互可解释性理论体系』,并基于此理论,从三个角度来解释神经网络的内在机理。
1. 语义解释的理论基础:数学证明神经网络的决策逻辑是否可以被少量符号化逻辑所充分覆盖(充分解释)。『证明神经网络的决策逻辑是否可以被有限符号化逻辑解释清楚』这一命题是解释神经网络的根本命题。如果此命题被证伪,则从根本上讲,神经网络的可解释性将是无望的,所有的解释性算法只能提供近似的解读,而无法精确地覆盖所有的决策逻辑。幸运的是,我们找到了在大部分应用中神经网络都可以满足的面向遮挡鲁棒性的三个常见的条件,并且数学证明了满足这三个条件的神经网络的决策逻辑可以被写成符号化的交互概念。
参见 https://zhuanlan.zhihu.com/p/693747946
2. 寻找性能指标背后的可证明、可验证的根因:将神经网络泛化性和鲁棒性等终极性能指标的根因拆分具体少数细节逻辑。对神经网络性能(鲁棒性、泛化性)的解释是神经网络可解释性领域的另一个重大问题。然而,目前人们普遍认为神经网络性能是对神经网络整体的描述,而神经网络无法像人类一样将自己的分类判断拆解成具象化的、少量的决策逻辑。在这方面,我们给出了不一样的观点 —— 将性能指标与具象化的交互之间建立起数学关系。我们证明了 1. 等效交互的复杂度可以直接决定神经网络的对抗鲁棒性 / 迁移性,2. 交互的复杂度决定了神经网络的表征能力,3. 并解释神经网络的泛化能力 [1],和 4. 解释神经网络的表征瓶颈。
- 参见1:https://zhuanlan.zhihu.com/p/369883667
- 参见2:https://zhuanlan.zhihu.com/p/361686461
- 参见3:https://zhuanlan.zhihu.com/p/704760363
- 参见4:https://zhuanlan.zhihu.com/p/468569001
3. 统一工程性深度学习算法。由于缺少基础理论的支撑,目前深度学习算法大都是经验性的、工程性的。可解释性领域的第一性原理应该可以承担起将前人的大量工程性经验总结为科学规律的任务。在等效交互可解释性理论体系下,我们团队既证明了 14 种不同的输入重要性归因算法的计算本质在数学上都可以统一写成对交互作用的再分配形式。此外,我们还统一了 12 种提升对抗迁移性的算法,证明了所有提升对抗迁移性算法的一个公共机理是降低对抗扰动之间的交互效用,实现了对神经网络可解释性方向大部分工程性算法的理论凝练。
- 参见1:https://zhuanlan.zhihu.com/p/610774894
- 参见2:https://zhuanlan.zhihu.com/p/546433296
在等效交互可解释性理论体系下,我们的团队在之前的研究中已经成功发表了 20 篇 CCF-A 类和机器学习顶级会议 ICLR 论文,我们已经从理论和实验上充分解答了上述问题。
二、本文研究概述
沿着上述理论框架,在这篇知乎文章中,我们希望精确解释出神经网络训练过程中泛化性的变化规律,具体地涉及两篇论文。
- 1.Junpeng Zhang, Qing Li, Liang Lin, Quanshi Zhang,“Two-Phase Dynamics of Interactions Explains the Starting Point of a DNN Learning Over-Fitted Features”,in arXiv: 2405.10262
- 2.Qihan Ren, Yang Xu, Junpeng Zhang, Yue Xin, Dongrui Liu, Quanshi Zhang,“Towards the Dynamics of a DNN Learning Symbolic Interactions” in arXiv:2407.19198

图 1:两阶段现象的示意图。在第一阶段,神经网络逐渐消除中高阶交互,学习低阶交互;在第二阶段,神经网络逐渐建模阶数不断增大的交互。当神经网络训练过程中测试损失和训练损失之间的 loss gap 开始增大时,神经网络恰好也进入训练的第二阶段。
我们希望在等效交互框架里提出新的理论,精确预测出神经网络每一个时间点上神经网络所学到的交互概念的数量、复杂度,以及泛化性变化的动力学规律(如图 1 所示)。具体地,我们希望证明出两方面结论。
第一,基于前人的证明(一个神经网络的决策逻辑可以被严格解构表示为几十个交互概念效用的和的形式),进一步严格推导出在整个训练过程中,神经网络所建模的交互效用的变化动力学过程 —— 即理论需精确预测出在不同训练阶段,神经网络所建模的交互概念的分布的变化 —— 推导出哪些交互会在哪个时间点上被学习到。
第二,寻找充分的证据,证明所推导的交互复杂度的变化规律客观反映出神经网络在全训练周期中泛化性变化的规律。
综上两点,我们希望具体彻底解释清楚神经网络的泛化性变化的内在根因。
与前人的关系:当然大家可能第一反应想到神经正切核(NTK)[2],但是神经正切核只是把参数的变化曲线解了出来,而没办法进一步深入到决策逻辑层面进行解释,没有将神经网络建模的概念表征与其泛化性的关系建立起来,对泛化性的分析依然停留在特征空间分析的层面,而没有在【符号化概念逻辑】与【泛化性】之间建立起严格的关系。
三、两大研究背景
误会 1:神经网络的第一性表征是『等效交互』,而不是神经网络的参数和结构。单纯从结构层面分析神经网络是人们对神经网络泛化根本表征的误解。目前大部分神经网络泛化性研究主要着眼于神经网络的结构、特征、以及数据。人们认为不同的神经网络结构就自然对应不同的函数,并自然展现出不同的性能。
但是,事实上,如图 2 所示,结构的区别只是神经网络表征的表面形式。除去有明显缺陷的对性能有明显影响的神经网络,所有其他可以实现 SOTA 性能的具有不同结构的神经网络往往都建模了相似的等效交互表征,即不同结构的高性能神经网络在等效交互表征上往往都是殊途同归的 [3, 4]。虽然神经网络其中层特征内部是复杂的混乱的,虽然不同神经网络所建模的特征向量大相径庭,虽然神经网络中单个神经元往往建模了相对比较混乱的语义(不是严格清晰的语义),但是神经网络作为一个整体,我们从理论上证明神经网络的所建模的交互关系是稀疏的符号化的(而不是特征的稀疏性,具体见 “四、交互的定义” 章节),而且面向相同任务的完全不同的神经网络往往建模了相似的交互关系。
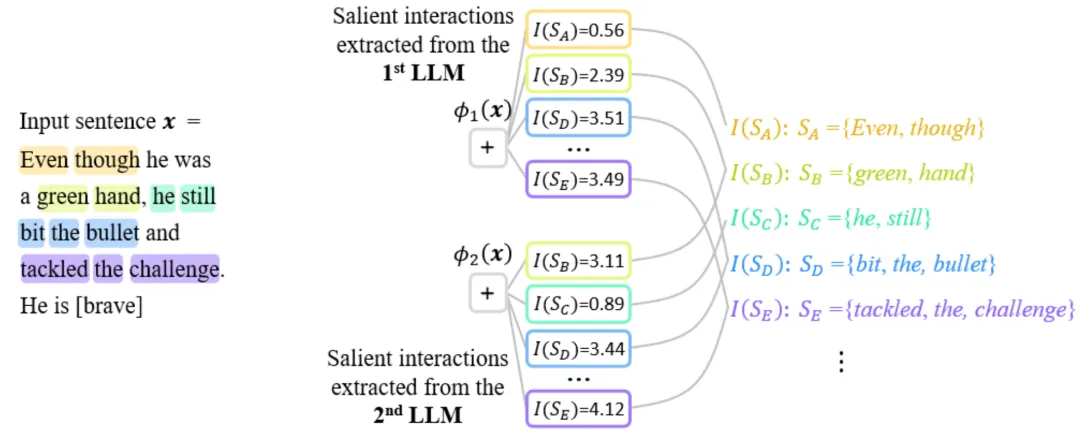
图 2:不同结构的神经网络所建模的等效交互往往是殊途同归的。对于一个相同的输入句子,面向两个相同任务的两个完全不同的神经网络建模往往相似的交互。
由于不同神经网络的参数和训练样本不一样,两个神经网络中没有任何一个神经元在表征上具有严格的一一对应关系,且每一个神经元往往建模着不同语义的混合模式。相比之下,正如上段分析,神经网络所建模的交互表征实际上是不同神经网络表征中的不变量。因此,我们有理由认为神经网络根本表征是等效交互,而不是其载体(参数和训练样本),符号化交互表征可能代表了知识表征的第一性原理(被交互的稀疏性定理、无限拟合性定理、以及殊途同归现象所保证,见 “四、交互的定义” 章节,具体详细研究见下面知乎文章。
参见:https://zhuanlan.zhihu.com/p/633531725
误会 2:神经网络的泛化性问题是一个混合模型问题,而不是一个高维空间的向量。如图 3 所示,传统的泛化性分析总是假设单个样本整体是高维空间的一个点,实际上神经网络对单个样本的表征是 mixture model 的形式 —— 实际上通过大量不同的交互来表达。我们发现简单交互的泛化能力比复杂交互的泛化能力更强,所以不再适合用一个简单标量来笼统表示整个神经网络在不同样本上的泛化能力。相反,同一个神经网络在不同的样本上建模了不同复杂度的交互关系,而不同复杂度的交互往往对应着不同泛化能力。通常情况下,神经网络建模的高阶(复杂)的交互往往难以泛化到测试样本上(测试样本上不会触发相同的交互),代表过拟合表征,而神经网络建模的低阶(简单)交互往往代表泛化性较强的表征,具体详细研究见 [1]。
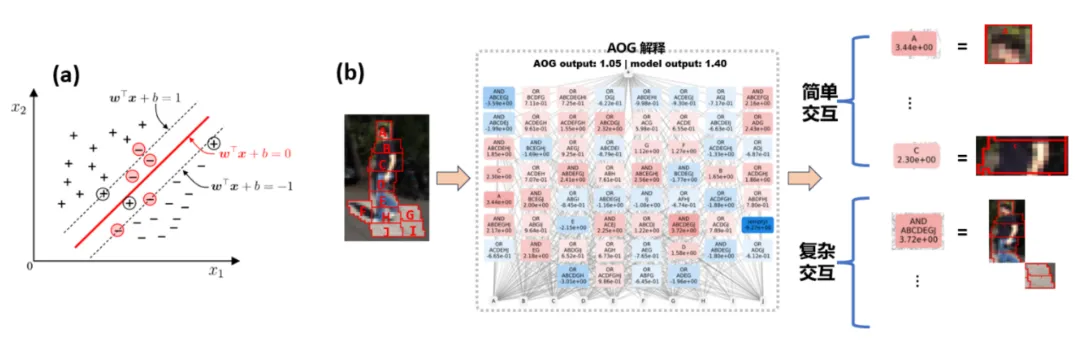
图 3:(a)传统的泛化性分析总是假设单个样本整体是高维空间的一个点。(b)实际上神经网络对单个样本的表征是 mixture model 的形式,神经网络在单个样本会建模简单交互(可泛化的交互)和复杂交互(不可泛化的交互)。
四、交互的定义
让我们考虑一个深度神经网络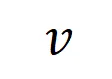 和一个输入样本
和一个输入样本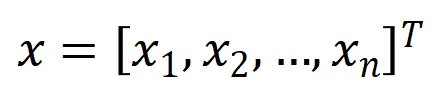 ,它包含
,它包含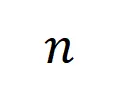 个输入变量,我们用集合
个输入变量,我们用集合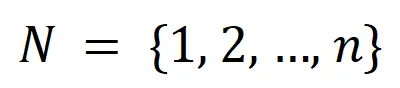 表示这些输入变量的全集。令
表示这些输入变量的全集。令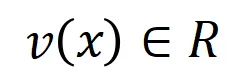 表示 DNN 在样本
表示 DNN 在样本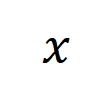 上的一个标量输出。对于一个面向分类任务的神经网络,我们可以从不同角度来定义其标量输出。例如,对于多类别分类问题,
上的一个标量输出。对于一个面向分类任务的神经网络,我们可以从不同角度来定义其标量输出。例如,对于多类别分类问题,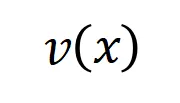 可以定义为
可以定义为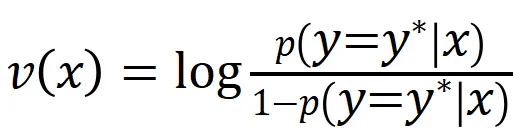 ,也可以定义为 softmax 层之前该样本真实标签所对应的标量输出。这里,
,也可以定义为 softmax 层之前该样本真实标签所对应的标量输出。这里,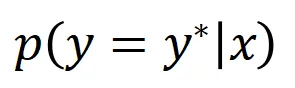 表示真实标签的分类概率。这样,针对每个子集
表示真实标签的分类概率。这样,针对每个子集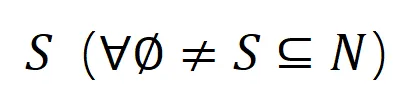 ,我们可以用下面公式来定义
,我们可以用下面公式来定义 中所有输入变量之间 “等效与交互” 和 “等效或交互”。
中所有输入变量之间 “等效与交互” 和 “等效或交互”。
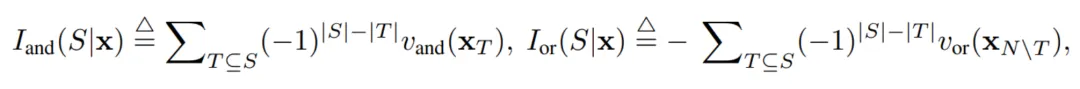
如图 4(a)所示,我们可以这样理解上述与或交互:我们可以认为与等效交互表示神经网络所编码的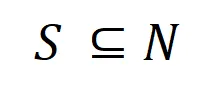 内输入变量之间的 “与关系”。例如,给定一个输入句子
内输入变量之间的 “与关系”。例如,给定一个输入句子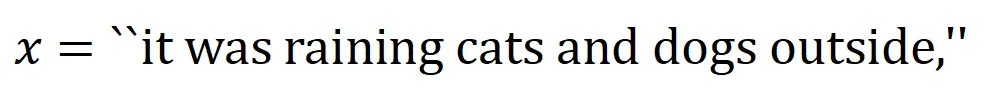 ,神经网络可能会在
,神经网络可能会在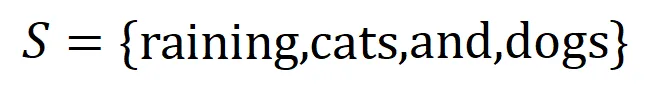 之间建模一个交互,使得
之间建模一个交互,使得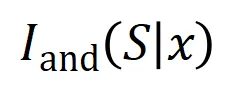 产生一个推动神经网络输出 “倾盆大雨” 的数值效用。如果
产生一个推动神经网络输出 “倾盆大雨” 的数值效用。如果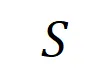 中的任何输入变量被遮挡,则该数值效用将从神经网络的输出中移除。类似地,等效或交互
中的任何输入变量被遮挡,则该数值效用将从神经网络的输出中移除。类似地,等效或交互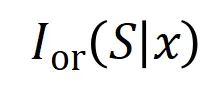 表示神经网络所建模的
表示神经网络所建模的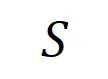 内输入变量之间的 “或关系”。例如,给定一个输入句子
内输入变量之间的 “或关系”。例如,给定一个输入句子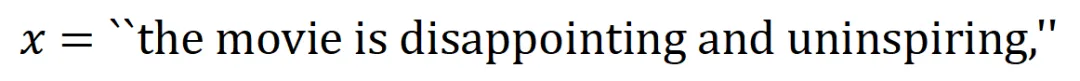 ,只要
,只要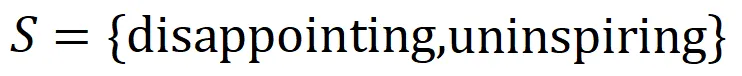 中的任意一个词出现,就会推动神经网络的输出负面情感分类。
中的任意一个词出现,就会推动神经网络的输出负面情感分类。
神经网络所建模的等效交互满足 “理想概念” 的三条公理性准则,即无限拟合性、稀疏性、样本间迁移性。
- 无限拟合性:如图 4,5 所示,对于任意遮挡样本,神经网络在样本上的输出可以用不同交互概念的效用之和来拟合。即,我们可以构造出一个基于交互的 logical model,无论我们如何遮挡输入样本,这个 logical model 依然可精确拟合模型在此输入样本在任意遮挡状态下的输出值。
- 稀疏性:面向分类任务的神经网络往往只建模少量的显著交互概念,而大部分交互概念都是数值效用都接近于 0 的噪声。
- 样本间迁移性:交互在不同样本间是可迁移的,即神经网络在(同一类别的)不同样本上建模的显著交互概念往往有很大的重合。
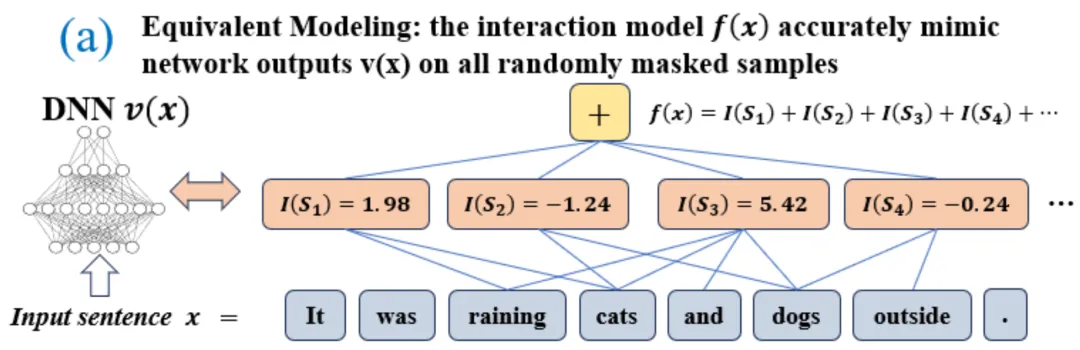
图 4:神经网络的复杂的推理逻辑可以被基于少量交互的逻辑模型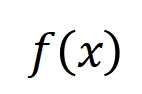 准确拟合。每个交互都是衡量神经网络建模特定输入变量集合
准确拟合。每个交互都是衡量神经网络建模特定输入变量集合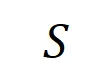 之间非线性关系的度量指标。当且仅当集合中变量同时出现时才会触发与交互,并为输出贡献数值分数
之间非线性关系的度量指标。当且仅当集合中变量同时出现时才会触发与交互,并为输出贡献数值分数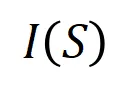 ,集合
,集合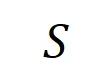 中任意变量出现时会触发或交互。
中任意变量出现时会触发或交互。
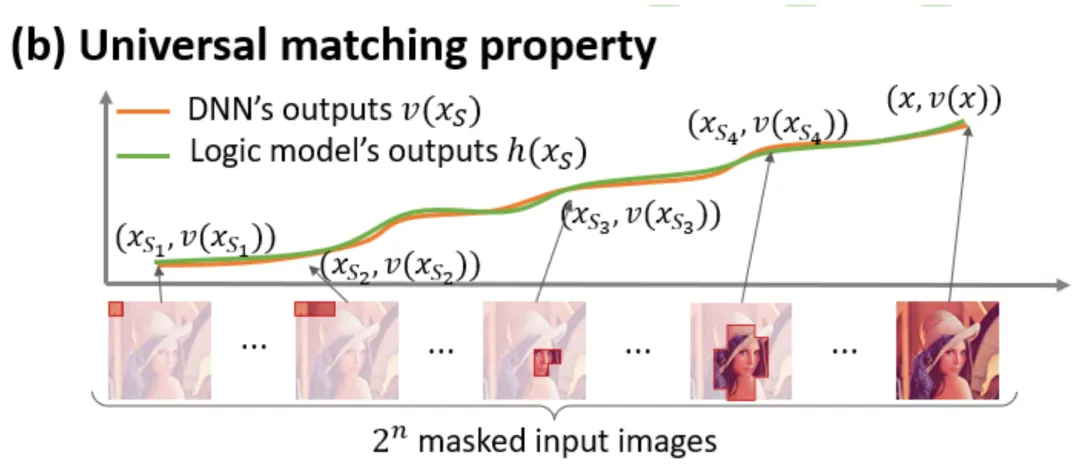
图 5:神经网络在任意的遮挡样本上的输出可以用不同交互概念的效用之和来拟合,即我们可以构造出一个基于交互的 logical model,无论我们如何遮挡输入样本,哪怕穷举个输入单元上种完全不同的遮挡方式,这个 logical model 依然可精确拟合模型在此输入样本在任意遮挡状态下的输出值。
五、新的发现与证明
5.1 发现神经网络在训练过程中交互变化的两阶段现象
在这篇知乎文章中,我们关注神经网络解释性领域的一个根本问题,即如何从一个解析分析的角度去严格预测出神经网络在训练过程中泛化能力的变化情况,并且精确的分析神经网络从欠拟合到过拟合的整个动态变化过程及其背后的根本原因。
首先,我们将交互的阶数(复杂度)定义为交互中的输入变量的数量,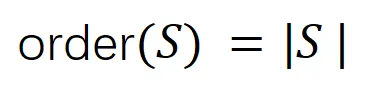 。我们团队之前的工作发现神经网络在某个特定样本所建模的 “与或交互” 的复杂度直接决定了神经网络在这个样本的泛化能力 [1],即神经网络建模的高阶的(大量输入单元之间的)“与或交互” 往往有较差的泛化能力,而低阶的(少量输入单元之间的)“与或交互” 具有较强的泛化能力。
。我们团队之前的工作发现神经网络在某个特定样本所建模的 “与或交互” 的复杂度直接决定了神经网络在这个样本的泛化能力 [1],即神经网络建模的高阶的(大量输入单元之间的)“与或交互” 往往有较差的泛化能力,而低阶的(少量输入单元之间的)“与或交互” 具有较强的泛化能力。
因此,本篇研究的第一步是去预测出神经网络在训练过程中不同时间点所建模的不同阶 “与或交互” 的复杂度的一个解析解,即我们可以通过神经网络在不同时间点所建模的不同阶 “与或交互” 的分布去解释神经网络在不同阶段的泛化能力。交互的泛化能力的定义与神经网络整体泛化能力的定义请见 “5.2 神经网络所建模交互的阶数和其泛化能力的关系” 章节。
我们提出两个指标来表示不同阶(复杂度)的交互的强度的分布。具体来说,我们用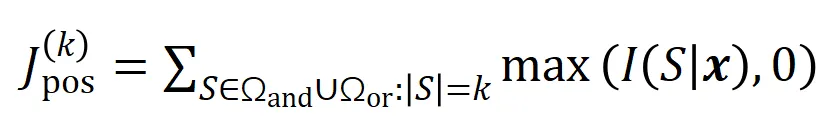 来衡量所有阶正显著交互的强度,用
来衡量所有阶正显著交互的强度,用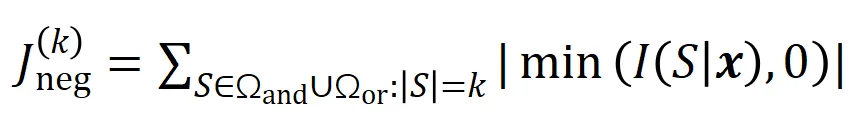 来衡量所有
来衡量所有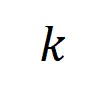 阶负显著交互的强度,其中
阶负显著交互的强度,其中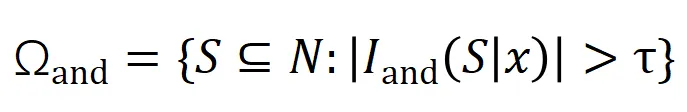 和
和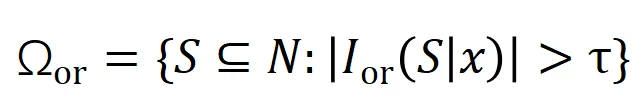 表示显著交互的集合,
表示显著交互的集合,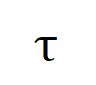 表示显著交互的阈值。
表示显著交互的阈值。
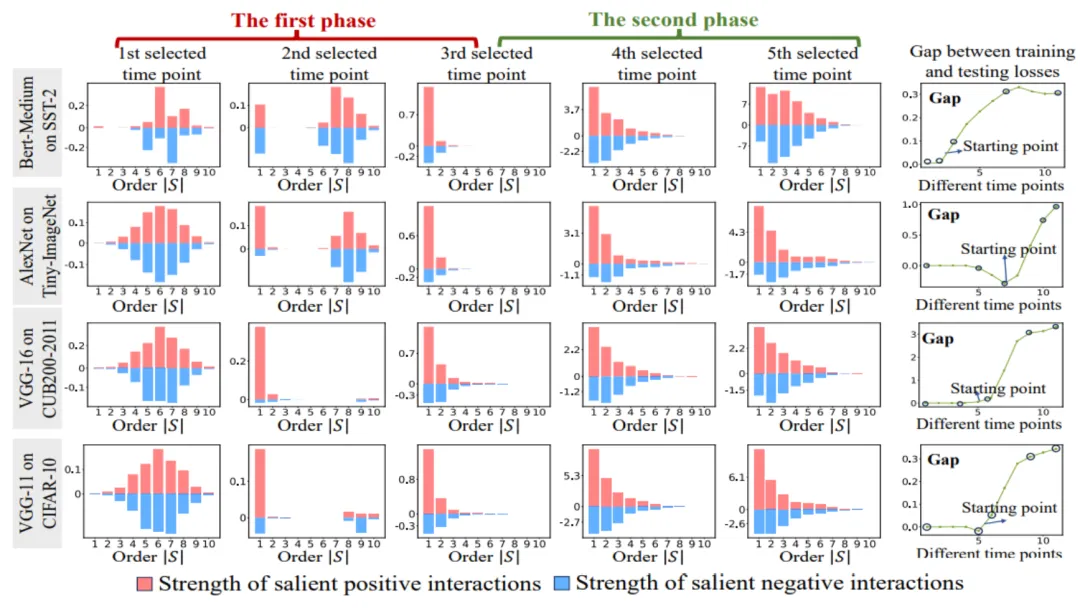
图 6:从训练不同轮次的神经网络中提取的不同阶交互强度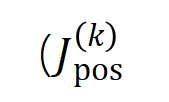 和
和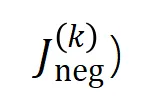 。在不同数据集上、不同任务上训练的不同的神经网络的训练过程都存在两阶段现象。前两个选定时间点属于第一阶段,而后两个时间点属于第二阶段。恰恰在进入神经网络训练过程的第二阶段不久,神经网络的测试损失和训练损失之间的 loss gap 开始显著上升(见最后一列)。这表明神经网络训练的两阶段现象与模型 loss gap 的变化在时间上是 “对齐” 的。更多实验结果请参见论文。
。在不同数据集上、不同任务上训练的不同的神经网络的训练过程都存在两阶段现象。前两个选定时间点属于第一阶段,而后两个时间点属于第二阶段。恰恰在进入神经网络训练过程的第二阶段不久,神经网络的测试损失和训练损失之间的 loss gap 开始显著上升(见最后一列)。这表明神经网络训练的两阶段现象与模型 loss gap 的变化在时间上是 “对齐” 的。更多实验结果请参见论文。
如图 6 所示,神经网络的两阶段现象具体表现为:
- 在神经训练训练之前,初始化的神经网络主要编码中阶交互,很少编码高阶和低阶交互,并且不同阶交互的分布看起来呈现 “纺锤形”。假设具有随机初始化参数的神经网络建模的是纯噪声,我们在 “5.4 理论证明两阶段现象” 章节证明了具有随机初始化参数的神经网络建模的不同阶的交互的分布呈现 “纺锤形”,即仅建模少量的低阶和高阶交互,大量建模中阶交互。
- 在神经网络训练的第一阶段,神经网络编码的高阶和中阶交互的强度逐渐减弱,而低阶交互的强度逐渐增强。最终,高阶和中阶交互逐渐被消除,神经网络只编码低阶交互。
- 在神经网络训练的第二阶段,神经网络在训练过程中编码的交互阶数(复杂度)逐渐增加。在逐渐学习更高复杂度的交互的过程中,神经网络过拟合的风险也在逐渐提高。
上述的两阶段现象广泛存在于不同结构的神经网络训练于不同任务上的不同数据集的训练过程中。我们在图像数据集(CIFAR-10 数据集、MNIST 数据集、CUB200-2011 数据集(使用从图片中裁剪出来的鸟类图像)和 Tiny-ImageNet 数据集)上训练了 VGG-11/13/16 和 AlexNet。我们在 SST-2 数据集上训练了用于情感语义分类 Bert-Medium/Tiny 模型,我们在 ShapeNet 数据集中训练 DGCNN 来分类的 3D 点云数据。上图显示了不同的神经网络在不同训练时期提取的不同阶的显著交互的分布。我们在这些神经网络的训练过程中都发现了两阶段现象,更多实验结果及细节请参考论文。
5.2 神经网络所建模交互的阶数和其泛化能力的关系
我们团队之前的工作已经发现了神经网络所建模交互的阶数和其泛化能力的关系,即高阶交互比低阶交互具有更差的泛化能力 [1]。某个具体交互的泛化性有清晰的定义 —— 如果一个交互同时在训练样本和测试样本中频繁的被神经网络所建模,则这个交互具有较好的泛化能力。在本篇知乎文章中,介绍了两个实验来证明高阶交互具有较差的泛化能力,低阶交互具有较强的泛化能力。
实验一:观察在不同数据集上训练的不同神经网络所建模的交互的泛化性。这里我们用被测试集所触发的交互的分布和被训练集所触发的交互的分布的 Jaccard 相似性来度量交互的泛化性。具体来说,给定一个包含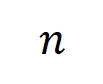 个输入变量的输入样本
个输入变量的输入样本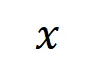 ,我们将从输入样本
,我们将从输入样本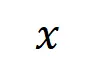 提取到的
提取到的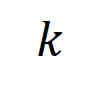 阶交互向量化
阶交互向量化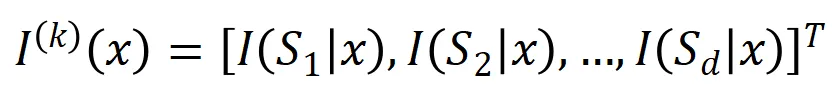 ,其中
,其中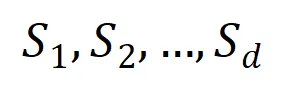 表示
表示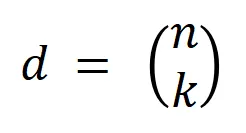 个
个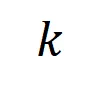 阶交互。然后,我们计算分类任务中所有类别为
阶交互。然后,我们计算分类任务中所有类别为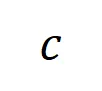 的样本中提取到的
的样本中提取到的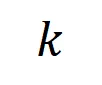 阶的平均交互向量,表示为
阶的平均交互向量,表示为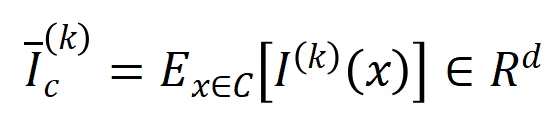 ,其中
,其中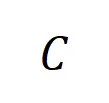 表示类别为
表示类别为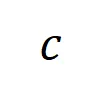 的样本的集合。接下来,我们计算从训练样本中提取的阶的平均交互向量
的样本的集合。接下来,我们计算从训练样本中提取的阶的平均交互向量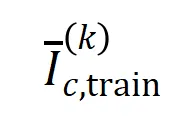 与从测试样本中提取的
与从测试样本中提取的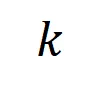 阶的平均交互向量
阶的平均交互向量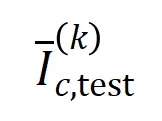 之间的 Jaccard 相似性,以衡量分类任务中类别为
之间的 Jaccard 相似性,以衡量分类任务中类别为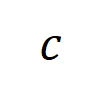 的样本的
的样本的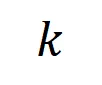 阶交互的泛化能力,即:
阶交互的泛化能力,即:
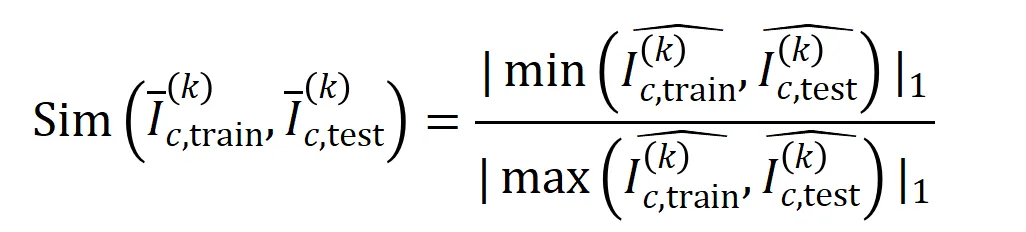
其中,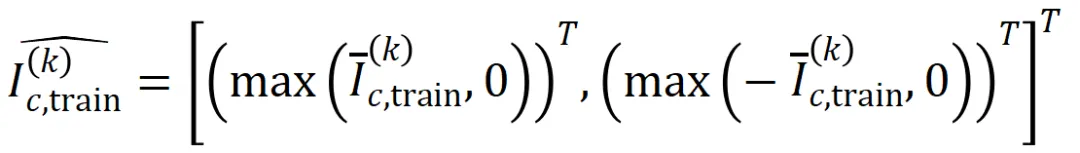 和
和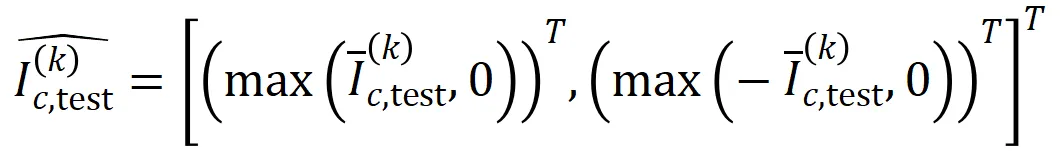 将两个
将两个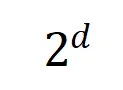 维交互向量投影到两个
维交互向量投影到两个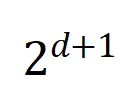 维的非负向量上,以便计算 Jaccard 相似性。对于某一阶的交互,如果此阶交互普遍展现出较大的 Jaccard 相似性,则表示这一阶交互具有较强的泛化能力。
维的非负向量上,以便计算 Jaccard 相似性。对于某一阶的交互,如果此阶交互普遍展现出较大的 Jaccard 相似性,则表示这一阶交互具有较强的泛化能力。
我们进行了实验计算不同阶交互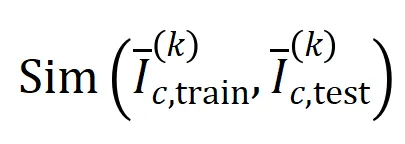 。我们测试了在 MNIST 数据集上训练的 LeNet、在 CIFAR-10 数据集上训练的 VGG-11、在 CUB200-2011 数据集上训练的 VGG-13,以及在 Tiny-ImageNet 数据集上训练的 AlexNet。为了减少计算成本,我们仅计算了前 10 个类别的 Jaccard 相似性的平均值
。我们测试了在 MNIST 数据集上训练的 LeNet、在 CIFAR-10 数据集上训练的 VGG-11、在 CUB200-2011 数据集上训练的 VGG-13,以及在 Tiny-ImageNet 数据集上训练的 AlexNet。为了减少计算成本,我们仅计算了前 10 个类别的 Jaccard 相似性的平均值 。如图 7 所示,随着交互阶数的增加,交互的 Jaccard 相似性不断下降。因此,这验证了高阶交互比低阶交互具有更差的泛化能力。
。如图 7 所示,随着交互阶数的增加,交互的 Jaccard 相似性不断下降。因此,这验证了高阶交互比低阶交互具有更差的泛化能力。
 图 7:从训练样本和测试样本中提取的交互之间的 Jaccard 相似性。低阶交互具有相对较高 Jaccard 相似性表明低阶交互具有较强的泛化能力。
图 7:从训练样本和测试样本中提取的交互之间的 Jaccard 相似性。低阶交互具有相对较高 Jaccard 相似性表明低阶交互具有较强的泛化能力。
实验二:比较神经网络在正常样本和 OOD 样本建模的交互的分布。我们比较了从正常样本中提取的交互与从分布外 (OOD) 样本中提取的交互,以检查神经网络在 OOD 样本上是否建模更多的高阶交互。我们将少量训练样本的分类标签设置为错误标签。这样,数据集中的原始样本可以视为正常样本,而一些带有错误标签的样本则对应于 OOD 样本,这些 OOD 样本可能会导致神经网络的过拟合。我们在 MNIST 数据集和 CIFAR-10 数据集上分别训练了 VGG-11 和 VGG-13。图 8 比较了从正常样本中提取的交互的分布和从 OOD 样本中提取的交互的分布。我们发现,VGG-11 和 VGG-13 在分类 OOD 样本时建模了更多复杂的交互(高阶交互),而在分类正常样本时则使用了较低阶的交互。这验证了高阶交互的泛化能力通常弱于低阶交互。
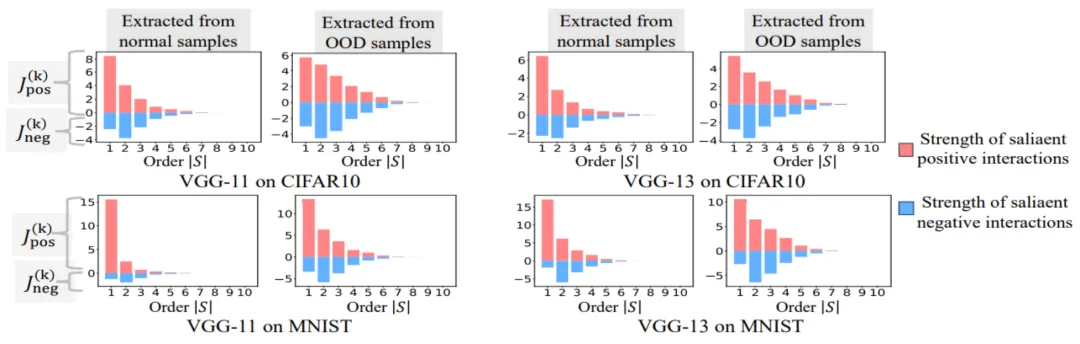
图 8:比较从正常样本中提取的交互与从分布外 (OOD) 样本中提取的交互。神经网络通常在 OOD 样本上建模的更高阶的交互。
5.3 两阶段现象和神经网络训练过程 loss gap 的变化相对齐
我们发现上述两阶段现象可以充分表示神经网络泛化性动力学。一个很有趣的现象是神经网络训练过程中的两阶段现象和神经网络在测试集和训练集的 loss gap 的变化在时间上是对齐的。训练损失和测试损失之间的 loss gap 是衡量模型过拟合程度的最广泛使用的指标。图 6 显示了不同的神经网络在训练工程的测试损失和训练损失之间的 loss gap 的曲线,还显示了从不同训练时期的神经网络中提取的交互分布。我们发现当神经网络训练过程中测试损失和训练损失之间的 loss gap 开始增大时,神经网络恰好也进入训练的第二阶段。这表明神经网络训练的两阶段现象与模型 loss gap 的变化在时间上是 “对齐” 的。
我们可以这样理解上述现象:在训练过程开始前,初始化的神经网络所建模的交互全部表示随机噪声,并且不同阶交互的分布看起来像 “纺锤形”。在神经网络训练的第一阶段,神经网络逐渐消除中阶和高阶的交互,并学习最简单的(最低阶的)交互。然后,在神经网络训练的第二阶段,神经网络建模了阶数逐渐增大的交互。由于我们在 “5.2 神经网络所建模交互的阶数和其泛化能力的关系” 章节中的两个实验验证了高阶交互通常比低阶交互具有更差的泛化能力,因此我们可以认为在神经网络训练的第二阶段,DNN 首先学习了泛化能力最强的交互,然后逐渐转向更复杂但泛化能力较弱的交互。最终一些神经网络逐渐过拟合,并编码了大量中阶和高阶交互。
5.4 理论证明两阶段现象
理论证明神经网络训练过程的两阶段现象共分为三个部分,第一部分我们需要证明随机初始化的神经网络在训练过程开始之前建模的交互的分布呈现 “纺锤形”,即很少建模高阶和低阶交互,主要建模中阶交互。第二部分证明神经网络在训练的第二阶段在建模阶数逐渐增大的交互。第三部分证明神经网络在训练的第一阶段逐渐消除中阶和高阶交互,学习最低价的交互。
1. 证明初始化神经网络建模的 “纺锤形” 交互分布。
由于随机初始化的随网络在训练过程开始之前建模的都是噪声,所以我们假设随机初始化的神经网络建模的交互的服从均值为 ,方差为
,方差为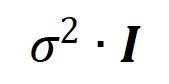 的正态分布。在上述假设下,我们能够证明初始化的神经网络建模的交互的强度和的分布呈现 “纺锤形”,即很少建模高阶和低阶交互,主要建模中阶交互。
的正态分布。在上述假设下,我们能够证明初始化的神经网络建模的交互的强度和的分布呈现 “纺锤形”,即很少建模高阶和低阶交互,主要建模中阶交互。

2. 证明神经网络训练的第二阶段的交互变化动态过程。
在进入正式的证明之前,我们需要做以下的预备工作。首先,我们参照 [5, 6] 的做法,将神经网络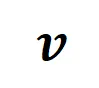 在特定样本上的 inference 改写为不同交互触发函数的加权和:
在特定样本上的 inference 改写为不同交互触发函数的加权和:
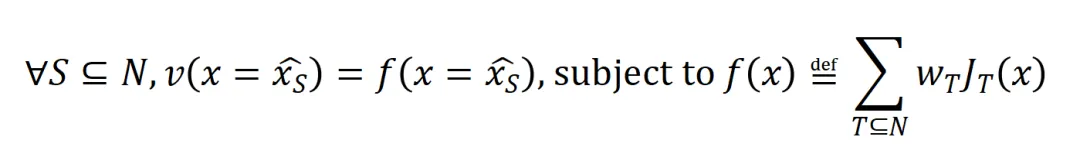
其中,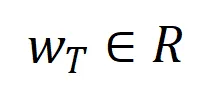 为标量权重,满足
为标量权重,满足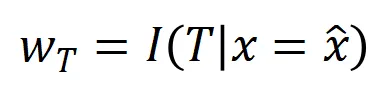 。而函数
。而函数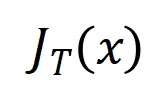 为交互触发函数,在任意一个遮挡样本
为交互触发函数,在任意一个遮挡样本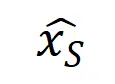 上都满足
上都满足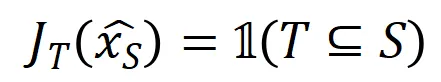 。函数
。函数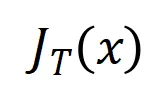 的具体形式可以由泰勒展开推导得到,可参考论文,这里不做赘述。
的具体形式可以由泰勒展开推导得到,可参考论文,这里不做赘述。
根据上述改写形式,神经网络在特定样本上的学习可近似看成是对交互触发函数的权重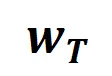 的学习。进一步地,实验室的前期工作 [3] 发现在同一任务上充分训练的不同的神经网络往往会建模相似的交互,所以我们可以将神经网络的学习看成是对一系列潜在的 ground truth 交互的拟合。由此,神经网络在训练到收敛时建模的交互可以看成是最小化下面的目标函数时得到的解:
的学习。进一步地,实验室的前期工作 [3] 发现在同一任务上充分训练的不同的神经网络往往会建模相似的交互,所以我们可以将神经网络的学习看成是对一系列潜在的 ground truth 交互的拟合。由此,神经网络在训练到收敛时建模的交互可以看成是最小化下面的目标函数时得到的解:
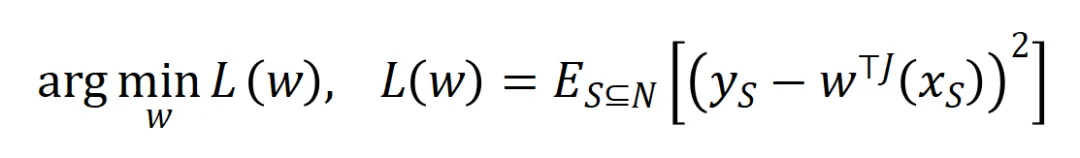
其中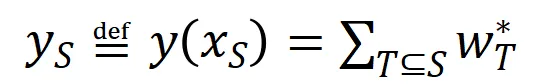 表示神经网络需要拟合的一系列潜在的 ground truth 交互。
表示神经网络需要拟合的一系列潜在的 ground truth 交互。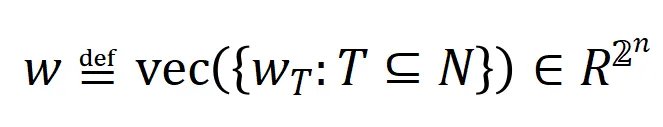 和
和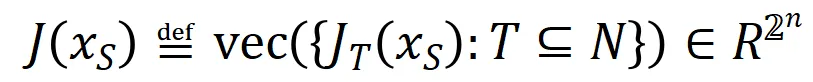 则分别表示将所有权重拼起来得到的向量和将所有交互触发函数的值拼起来得到的向量。
则分别表示将所有权重拼起来得到的向量和将所有交互触发函数的值拼起来得到的向量。
可惜的是,上述建模虽然能得到神经网络训练到收敛时的交互,但是无法很好地刻画神经网络训练过程中学习交互的动态过程。这里引入我们的核心假设:我们假设初始化神经网络的参数上包含了大量噪声,而这些噪声的量级在训练过程中逐步变小。而进一步地,参数上的噪声会导致交互触发函数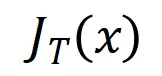 上的噪声,且该噪声随着交互阶数指数级增长 (在 [5] 中已有实验上的观察和验证) 。我们将有噪声下的神经网络的学习建模如下:
上的噪声,且该噪声随着交互阶数指数级增长 (在 [5] 中已有实验上的观察和验证) 。我们将有噪声下的神经网络的学习建模如下:
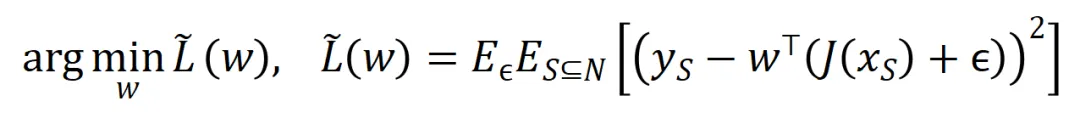
其中噪声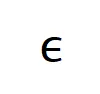 满足
满足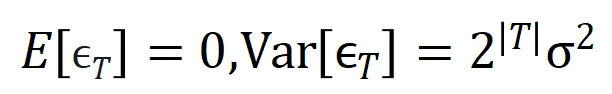 。且随着训练进行,噪声的方差
。且随着训练进行,噪声的方差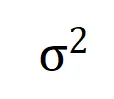 逐渐变小。
逐渐变小。
在给定的噪声量级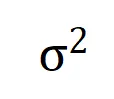 的情况下最小化上述损失函数,可得到最优交互权重
的情况下最小化上述损失函数,可得到最优交互权重 的解析解,如下图中的定理所示。
的解析解,如下图中的定理所示。

我们发现,随着训练进行(即噪声量级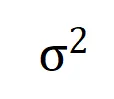 变小),中低阶交互强度和高阶交互强度的比值逐渐减小(如下面的定理所示)。这解释了训练的第二阶段中神经网络逐渐学到更加高阶的交互的现象。
变小),中低阶交互强度和高阶交互强度的比值逐渐减小(如下面的定理所示)。这解释了训练的第二阶段中神经网络逐渐学到更加高阶的交互的现象。

另外,我们对上述结论进一步做了实验验证。给定一个具有 n 个输入单元的样本,指标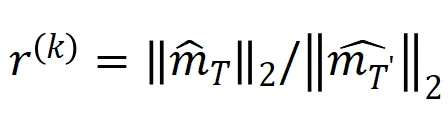 ,其中
,其中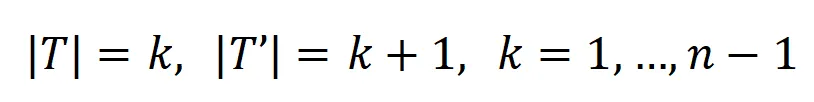 , 可以用来近似测量第 k 阶交互和第 k+1 阶交互强度的比值。在下图中,我们可以发现,在不同的输入单元个数 n 和不同的阶数 k 下,该比值都会随着
, 可以用来近似测量第 k 阶交互和第 k+1 阶交互强度的比值。在下图中,我们可以发现,在不同的输入单元个数 n 和不同的阶数 k 下,该比值都会随着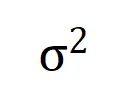 的减小而逐渐减小。
的减小而逐渐减小。

图 9:在不同的输入单元个数 n 和不同的阶数 k 下,第 k 阶交互和第 k+1 阶交互强度的比值都会随着噪声量级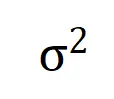 的减小而逐渐减小。这说明随着训练进行(即
的减小而逐渐减小。这说明随着训练进行(即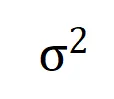 逐渐变小),低阶交互强度与高阶交互强度的比值逐渐变小,神经网络逐渐学到更加高阶的交互。
逐渐变小),低阶交互强度与高阶交互强度的比值逐渐变小,神经网络逐渐学到更加高阶的交互。
最后,我们对比了在不同噪声量级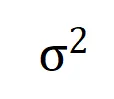 下的理论交互值
下的理论交互值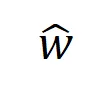 在各个阶数上的分布
在各个阶数上的分布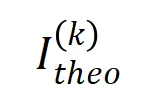 和实际训练过程中各阶交互的分布
和实际训练过程中各阶交互的分布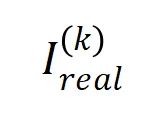 ,发现理论交互分布可以很好地预测实际训练中各时间点的交互强度分布。
,发现理论交互分布可以很好地预测实际训练中各时间点的交互强度分布。
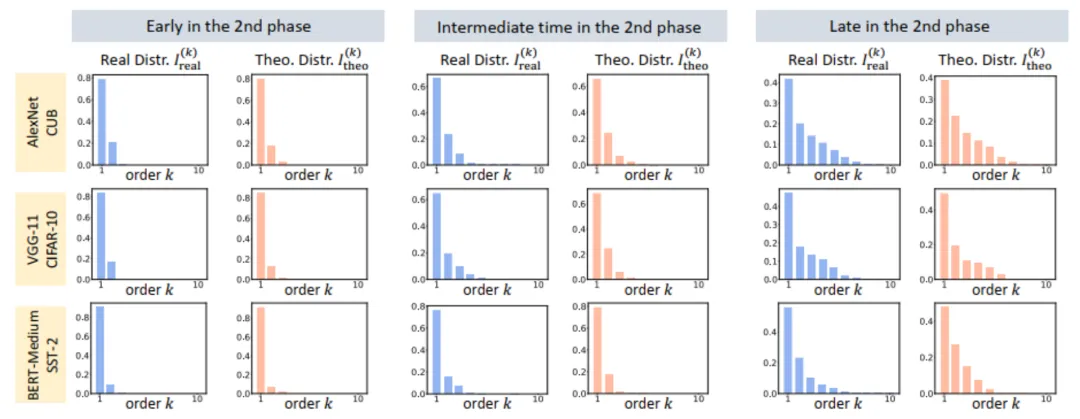
图 10:比较理论交互分布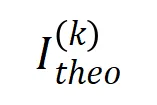 (蓝色直方图)和实际交互分布
(蓝色直方图)和实际交互分布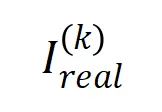 (橙色直方图)。在训练第二阶段的不同时间点,理论交互分布都可以很好地预测和匹配实际交互的分布。更多结果请参见论文。
(橙色直方图)。在训练第二阶段的不同时间点,理论交互分布都可以很好地预测和匹配实际交互的分布。更多结果请参见论文。
3. 证明神经网络训练的第一阶段的交互变化动态过程。
如果说训练的第二阶段中交互的动态变化可以解释为权重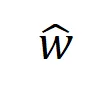 的最优解在噪声
的最优解在噪声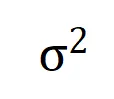 逐渐减小时的变化,那么第一阶段就可认为是交互从初始化的随机交互逐渐收敛到最优解的过程。
逐渐减小时的变化,那么第一阶段就可认为是交互从初始化的随机交互逐渐收敛到最优解的过程。
路漫漫其修远兮,我们团队是做神经网络可解释性的第一性原理,我们希望在更多的方面把这个理论做扎实,能够严格证明等效交互是符号化的解释,并且能够解释神经网络的泛化性、鲁棒性,同时证明神经网络表征瓶颈,统一 12 种提升神经网络对抗迁移性的方法和解释 14 种重要性估计方法。我们后面会做出更扎实的工作,进一步完善理论体系。







































