发一篇顶会论文,需要多少实验预算?
最近,DeepMind发表了一项研究,对LLM扩大规模时各种算法和架构细节,比如参数和优化器的选择,进行了广泛的实证调查。
这篇论文已被ICML 2024接收。

论文地址:https://arxiv.org/abs/2407.05872
63页的论文涵盖了数以万计的模型,备选方案包括3种优化器、4种参数化方案、几种对齐假设、十多个学习率,以及最高达26.8B的14种参数规模。
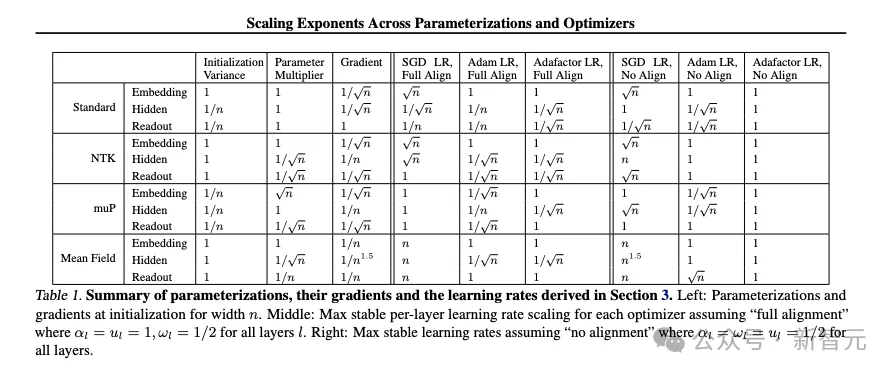
需要进行实验的4种参数化方案
仅仅听到这些数字,就不难知道,这项研究必定涉及海量的模型运行实验。
而有一位忠实读者,为了测试自己对论文内容的理解,统计了其中进行的所有实验,并估算出了复现论文的成本。
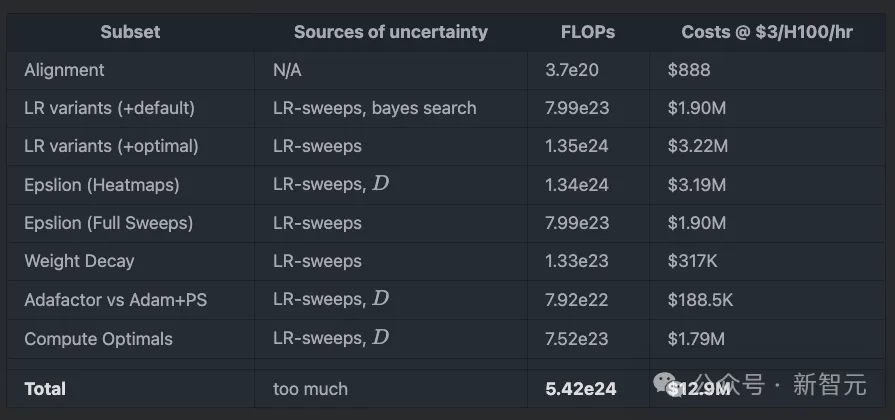
将所需算力全部加在一起,林林总总,居然达到了惊人的1290万美元。
考验基本功的时刻到了,假如你是研究团队的leader,根据实验计划对所需算力和成本进行预估是一项必不可少的技能。
那就让我们跟着这篇博客文章盘一遍,这一千多万美元,究竟烧在哪里。
Transformer架构信息
论文附录C提供了关于模型算法和架构的各种细节设置,比如使用decoder-only架构、层归一化、GeLU激活函数、无dropout、T5分词器、批大小为256、用FSDP并行等等。
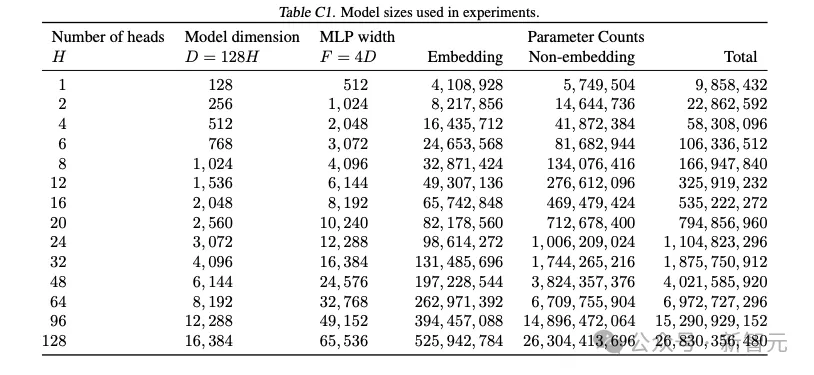
实验模型的参数规模统计
通过架构方面的信息,我们可以大致估算出训练中每个token所需的FLOPS,记为M。
由于论文没有描述到任何GQA/MQA机制,所以就假设Rkv=1,此外还有lseq=512,Dhead=128,L=8(深度),V=32101(分词器词汇量)。
模型总参数量可以表示为:

因此,就可以得到M的计算公式:

默认情况下,每次实验处理的token数(tokens per experiment, TPE)为5k(训练步数)×256(批大小)×512(lseq),约为6.5536e9。
def M(d: int, L=8, l_seq=512, V=32101) -> int:
return 6*d * (L*(12*d + l_seq) + V)
TPE = 50000 * 256 * 512对齐实验
假设对齐实验中,直接使用了后面的学习率扫描得出的最优结果,并没有单独进行学习率扫描,因此这一步的成本计算比较简单:

def alignment() -> int:
return 4 * TPE * sum(M(d) for d in [1024,2048,4096])
# >>> f'{alignment():.3E}'
# '3.733E+20'
# >>> cost_of_run(alignment())[0]
# 888.81395400704如果H100每运行1小时的花费以3美元计算,对齐实验的成本大致为888美元。
学习率
子问题:最佳评估损失(eval loss)实验
论文的表E1记录了6种模型规模下,所有可能的优化器×参数化方案×模型大小×实验设置的组合,分别进行基础学习率扫描,以获得最佳评估损失。

总共包括如下几个实验变量:
- 模型维度D∈3072,4096,6144,8192,12288,16384
- 4种参数化方案
- 3种优化器,其中SGD仅有5个实验设置,Adam和Adam+Param Scaling有7个实验设置
假设这里的实验都是单独进行,没有从其他地方复制结果,因此如果全部运行一遍,有成本上限预估:

H = [1,2,4,6,8,12,16,20,24,32,48,64,96,128]
D = [h * 128 for h in H]
def table_e1() -> int:
sets_x_optims = 5 + 7 + 7
return 4 * sets_x_optims * TPE * sum(M(d) for d in D[-6:])
# >>> f'{table_e1():.3E}';cost_of_run(table_e1())
# '1.634E+23'
# (388955.9991064986, 16206.499962770775)这部分的成本就接近40万美元,虽然仍属于可接受范围内,但对于大多数学术预算来说,已经算是非常昂贵了。
表E1给出了最佳评估损失,但没有描述LR的扫描策略,每张图上的点数也不尽相同。
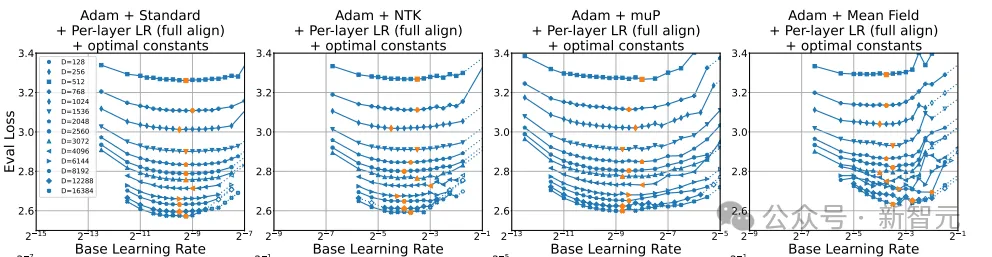
由于没有得到论文作者的答复,我们也无法确定具体机制,因此假设每个最佳评估损失都经过了15次实验(目测发现,每条线的点数约为10~15)。
β参数
根据论文4.2节内容,学习率还涉及到两个超参数的选择:β和γ。
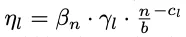
如果仅有β参数,则被称为「LR+default」设置:
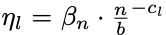
这部分包括3×优化器,4×参数化,加上全局和单层(GlobalLR、Perlayer-fullalign)分别进行实验,以及未知的LR扫描数量:

def beta_only() -> int:
return 3*4*2*PpL * TPE * sum(M(d) for d in D)
# 7.988E+23 (1902022.3291813303, 79250.93038255542)从公式就可以看出,成本和下文的epsilon实验类似,都是200万美元。
γ参数
相比β参数的实验,这部分有两个细节差异。
首先,除了GlobalLR、Perlayer-fullalign两种设置外,还需要加上Perlayer-noalign设置。

其次,仅针对d=1024=b,进行3D超参数搜索(γ_1,γ_h,γ_L+1),因此有额外的800次运行。

两者结合后的计算公式为:

这部分的预估成本与Adam的epsilon热力图实验接近,约为320万美元。
def gamma_expts() -> int:
return 36*TPE * (800*M(1024) + PpL*sum(M(d) for d in D))
# gamma_expts 1.354E+24 (3224397.534237257, 134349.8972598857)Adam优化器的Epsilon参数
论文4.3节所述的Epsilon参数实验是计算量的大头。
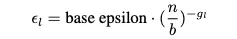
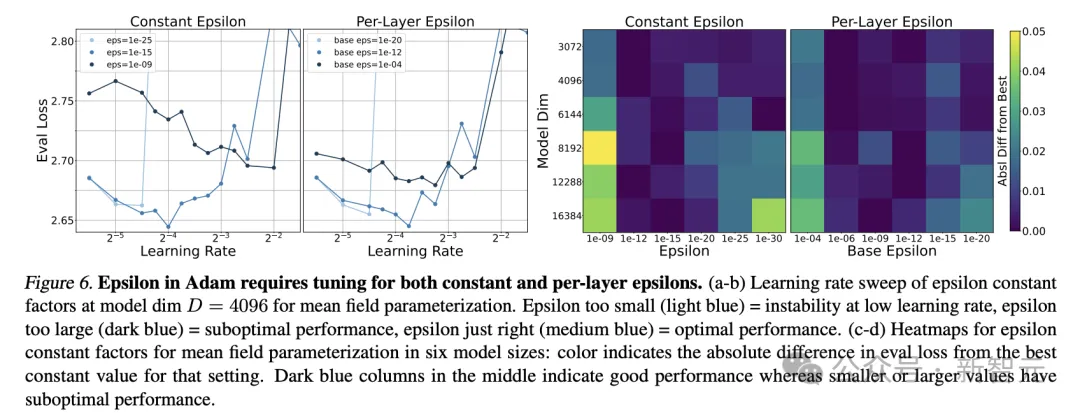
根据上面的推断,每次找到最佳评估损失时都尝试过15个不同的学习率(points per line),那么图6所示的epsilon参数变化图耗费的计算量为:

计算结果透露出一种简洁的昂贵,也就是200万美元的账单而已。
PpL = 15 # unprincipled estimate
def eps_variants() -> int:
return 4 * 6 * PpL * TPE * sum(M(d) for d in D)
'''
>>> f'{eps_variants():.3E}';cost_of_run(eps_variants())
'7.988E+23'
(1902022.3291813303, 79250.93038255542)
'''除了图6左侧的折线图,还有附录F热力图的结果。
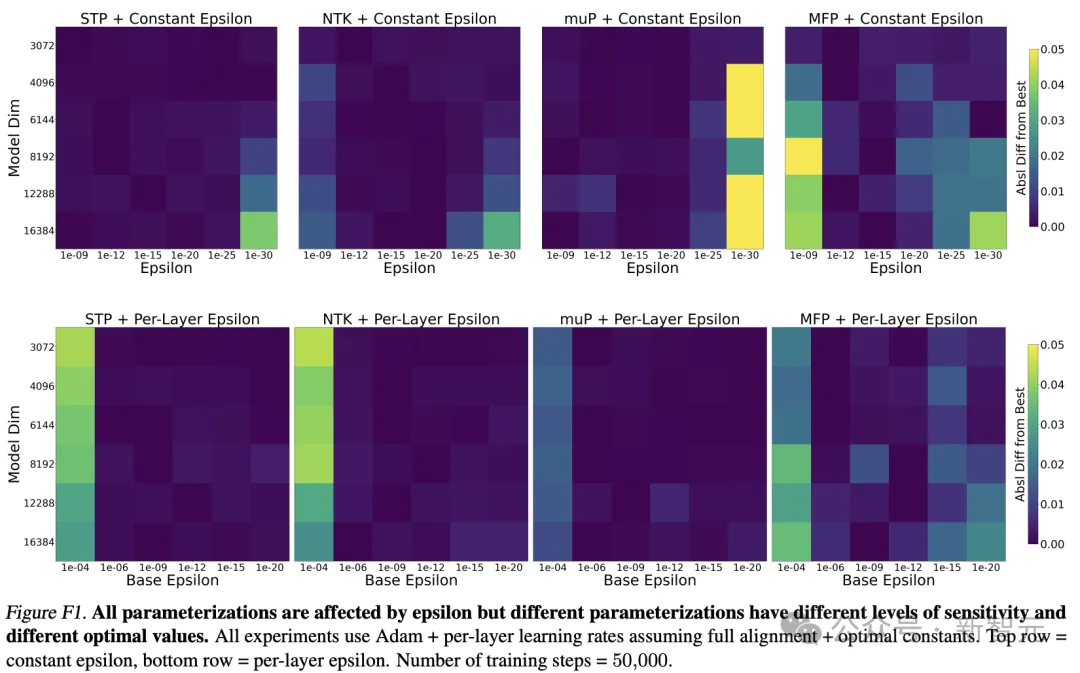
假设每个方块值都是经过13次学习率扫描后得到的结果,这部分计算量则为:

结果发现,仅仅要得到这8张热力图,成本就是320万美元。而且,由于我们将LR扫描数量建模为常数13,这个数字可能低于实际成本。
def eps_heatmaps() -> int:
# eps-type * eps-val * parameterizations * LR range * ...
return 2 * 6 * 4 * 13 * TPE * sum(M(d) for d in D[-6:])
'''
>>> f'{eps_heatmaps():.3E}';cost_of_run(eps_heatmaps())
'1.341E+24'
(3193533.466348094, 133063.89443117057)
'''权重衰减
权重衰减实验(附录G)比较好理解,对4×参数化方案以及所有参数进行一次基本的LR扫描:

比epsilon实验便宜不少,也就是湾区工程师一年的工资——31.7万美元。
def weight_decay() -> int:
return 4 * PpL * TPE * sum(M(d) for d in D)
'''
>>> f'{weight_decay():.3E}'; cost_of_run(weight_decay())
'1.331E+23'
(317003.7215302217, 13208.488397092571)
'''Adafactor优化器
这部分实验在附录C3中有详细描述,是为了检验Adafactor和Adam+parameter scaling是否有相似的宽度缩放机制。
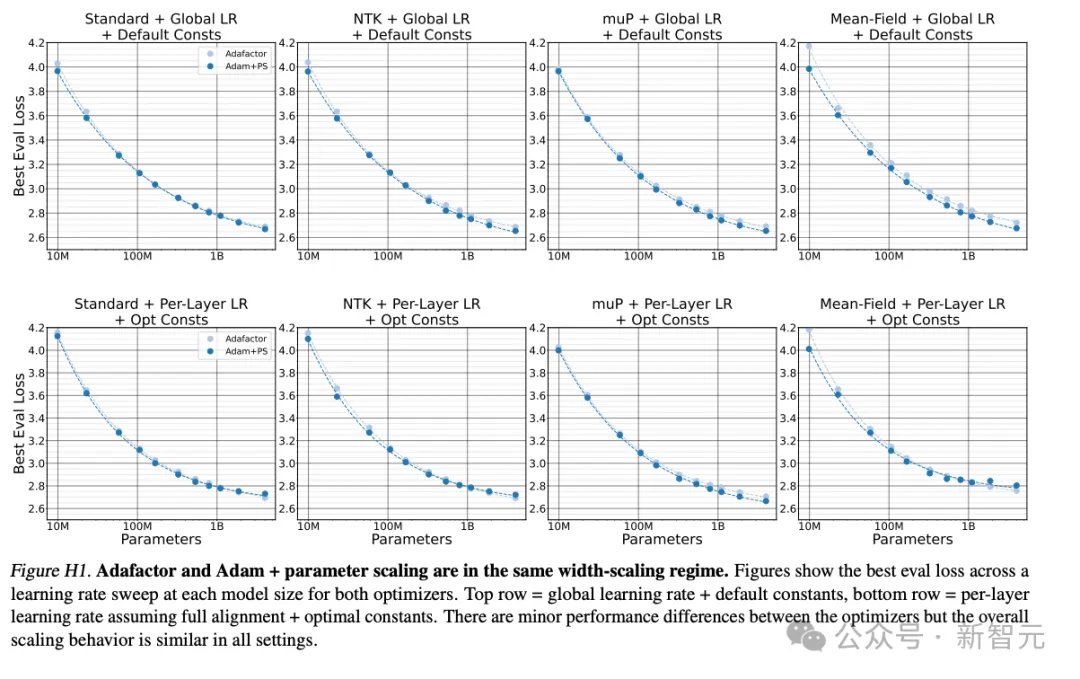
共有2×4张图,其中每个优化器收集11个数据点,因此计算公式为:

账单上再加18.8万美元。
def adafactor() -> int:
return 2*2*4*PpL*TPE*sum(M(d) for d in D[:11])
'''
>>> f'{adafactor():.3E}'; cost_of_run(adafactor())
'7.918E+22'
(188532.80765144504, 7855.533652143543)
'''计算最优化
论文尝试改变注意力头H的数量,希望找到计算最优化的设置,但其中涉及步长和数据集的改变,因此这部分不使用公式描述,计算代码如下:
def P(d: int, L=8, V=32101) -> int:
return 2 * d * (6*L*d + V)
def compute_optimal():
indices_50k = (14, 14, 12)
return 4*PpL*sum([
TPE * sum(sum( M(d) for d in D[:i] ) for i in indices_50k),
20 * sum(P(d)*M(d) for d in D[:11]) *3,
])
# compute_optim 7.518E+23 (1790104.1799513847, 74587.67416464102)总结
将以上各部分实验的算力和成本汇总在一起:
alignment 3.733E+20 (888.81395400704, 37.033914750293334)
table_e1 1.634E+23 (388955.9991064986, 16206.499962770775)
eps_variants 7.988E+23 (1902022.3291813303, 79250.93038255542)
eps_heatmaps 1.341E+24 (3193533.466348094, 133063.89443117057)
beta_only 7.988E+23 (1902022.3291813303, 79250.93038255542)
gamma_expts 1.354E+24 (3224397.534237257, 134349.8972598857)
weight_decay 1.331E+23 (317003.7215302217, 13208.488397092571)
adafactor 7.918E+22 (188532.80765144504, 7855.533652143543)
compute_optim 7.518E+23 (1790104.1799513847, 74587.67416464102)结果发现,整篇论文的运算量为5.42e24 FLOPS。
这个数字仅仅是Llama 3训练计算量的15%,如果在10万卡H100集群上运行,只需要2天时间即可完成所有实验。
total_flops=5.421E+24
rental price: US$12.9M
h100 node months required: 746.9595590938408
(sanity check) D=[128, 256, 512, 768, 1024, 1536, 2048, 2560, 3072, 4096, 6144, 8192, 12288, 16384]
(sanity check) model sizes: ['0.00979B', '0.0227B', '0.058B', '0.106B', '0.166B', '0.325B', '0.534B', '0.794B', '1.1B', '1.87B', '4.02B', '6.97B', '15.3B', '26.8B']
(sanity check) M/6P: ['63.4%', '68.5%', '75.3%', '79.7%', '82.8%', '86.8%', '89.3%', '91.0%', '92.2%', '93.9%', '95.7%', '96.7%', '97.7%', '98.3%']然而,如果不从LLM预训练的标准来衡量,仅把DeepMind的这篇论文看做一篇学术研究,这个计算量就显得相当奢侈了。
如果实验室仅有10张H100,就根本不可能进行这个量级的研究。
有100张H100的大型实验室,或许能用几年时间跑完以上所有实验。