大语言模型(LLM)通常过于庞大,无法在消费级硬件上运行。这些模型的参数可能超过数十亿,通常需要显存较大的GPU来加速推理过程。
因此,越来越多的研究开始关注如何缩小模型,比如改进训练方法或使用适配器。该领域的一项主要技术被称为量化(quantization)。
ML工程师Maarten Grootendorst撰写了一篇博客文章,在语言建模背景下专门介绍了量化技术,并通过可视化的方法逐一探索相关概念,以帮助我们建立对该技术的直观理解。

在这篇博文中,Maarten将探讨各种方法、使用案例以及量化背后的原理。
文章目录以及涵盖内容如下图所示,主要介绍了训练后量化(PTQ)以及量化感知训练(QAT)两种方法,建议有AI基础的读者直接跳转至对称量化部分:

第一部分:LLM的「问题」
「大语言模型」就是大在模型参数量上,规模通常达到数十亿的级别(其中主要是权重)。
这些参数不仅存储成本相当高,推理阶段的计算量也很大。
在推理过程中,激活值是输入和权重的乘积,因此权重数量越多,激活值也会越大。
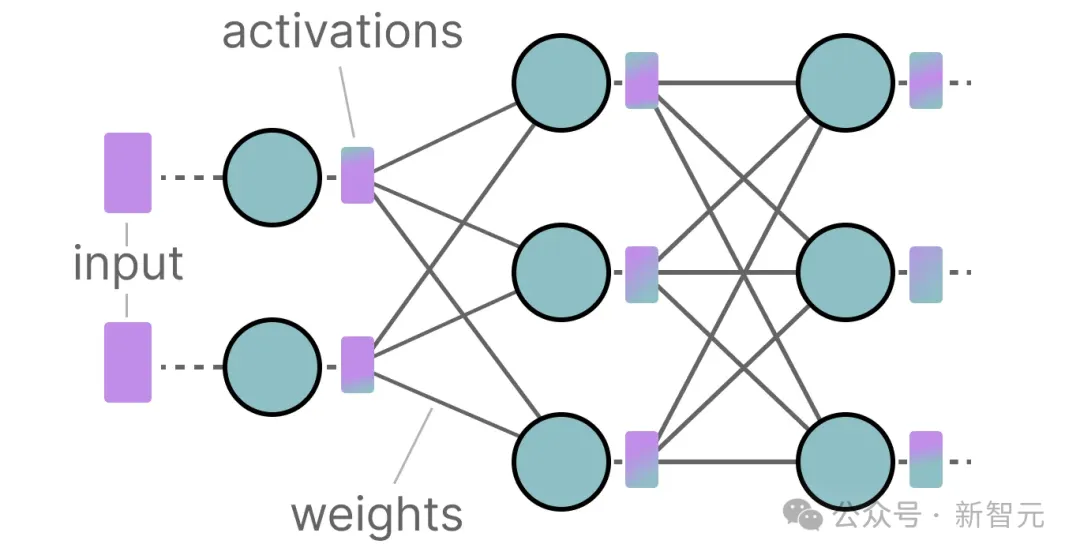
因此,我们希望尽可能高效地表示数十亿个值,从而尽可能减少存储参数所需的空间。
让我们从头开始,探索数值是如何表示的,然后再进行优化。
如何表示数值
数值存储的形式通常是浮点数(floting point number,或简称为floats):一个带有小数点的正数或负数。
这些值由每一位(bit)上的二进制数字表示。
IEEE-754标准描述了每一位上的数字如何表示具体数值,具体来说共有三种映射:符号、指数或小数(尾数)。
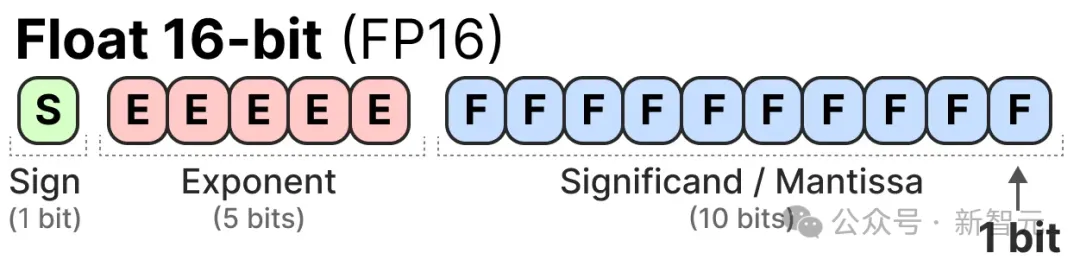
这三个部分可以结合起来,根据一组bit值计算出所表示的数值:
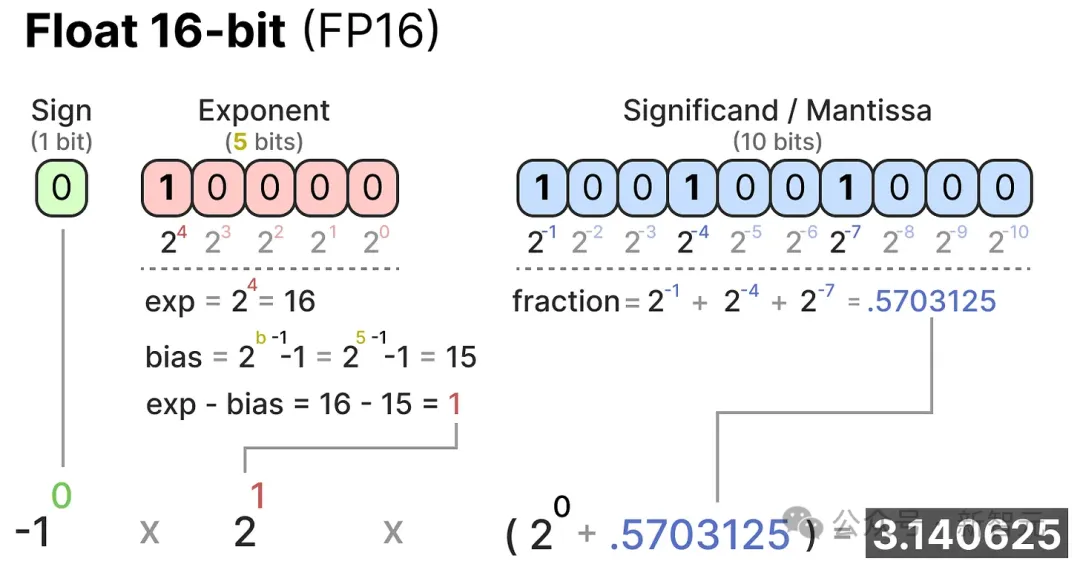
使用的位数越多,表示的数值值通常越精确,比如FP32形式就能比FP16精确到小数点后更多位数:

内存限制
可用的位数越多,不仅数值越精确,可表示的数值范围也越广。

给定位数和表示形式,可表示的数值区间称为动态范围(dynamic range),而两个相邻值之间的距离称为精度(precision)。

这种表达形式的一个巧妙特性在于,我们可以计算出设备需要多少内存来存储某个给定值。
由于内存中的每个字节含有8位,我们可以为大多数形式的浮点数创建一个基本公式——
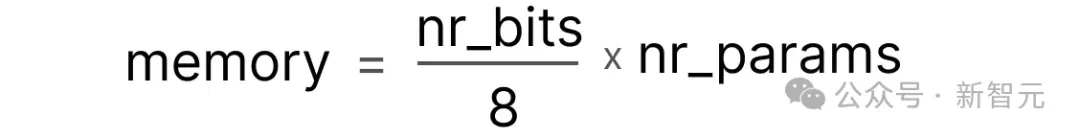
在实际应用中,还有更多因素会影响推理过程中所需的显存/内存大小,例如上下文大小和模型架构
现在假设我们有一个包含700亿参数的模型。大多数模型本身使用32位浮点数(通常称为全精度)表示,这需要280GB的内存来加载模型。
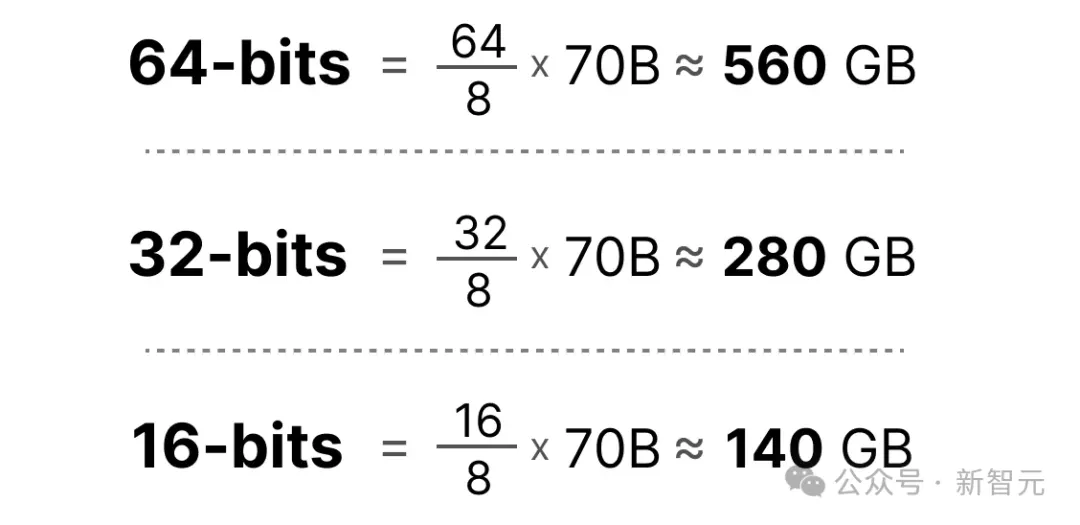
但如果能将所有参数用16位浮点数表示,所需的内存大小就可以直接减少一倍。
因此,将模型参数的表示位数最小化(不仅是推理,还有训练过程)是非常有吸引力的。
然而,这种方法不是没有代价的。随着表示位数减少导致精度降低,模型的准确性通常也会下降。
我们希望在保持准确性的同时减少表示数值的位数……此时,量化技术就派上用场了。
第二部分:量化入门
现在我们知道,量化的目的是将模型参数的精度从较高位宽(如32位浮点数)降低到较低位宽(如8位整数)。
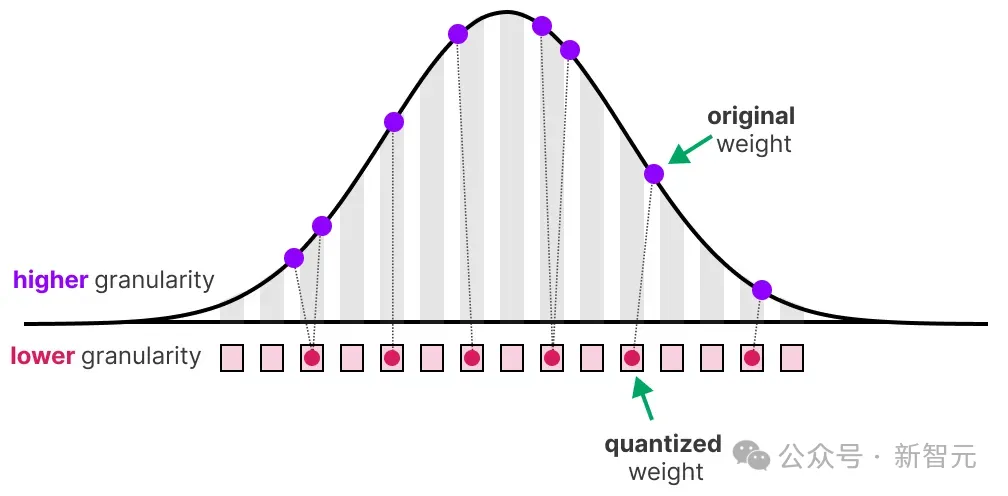
在减少表示原始参数的位数时,通常也会伴随一些精度(粒度,granularity)的损失。
为了让这种效果更直观,我们可以用照片颜色作为类比。比如,选择任意图像(左图),但只用8种颜色表示(右图):

注意看,放大的曲奇饼干看起来比原来更有「颗粒感」。
与之相似,量化的主要目标是减少表示原始参数所需的比特数(颜色),同时尽可能保留原始参数的精度。
常见数据类型
首先,让我们看看常见的数据类型以及使用它们替代32位(称为全精度或FP32)表示的影响。
FP16
首先是一个从32位到16位(称为半精度或FP16)浮点数的例子:
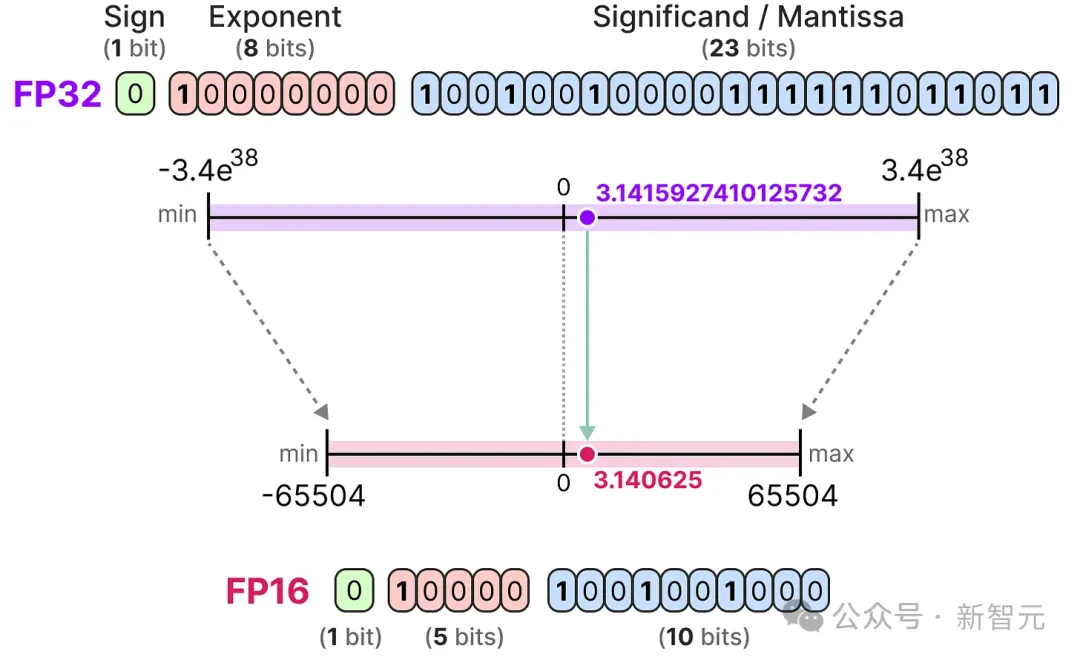
FP16可取的数值范围比FP32小得多。
BF16
为了获得与原始FP32相似的数值范围,引入了bfloat 16作为一种「截断的FP32」类型:
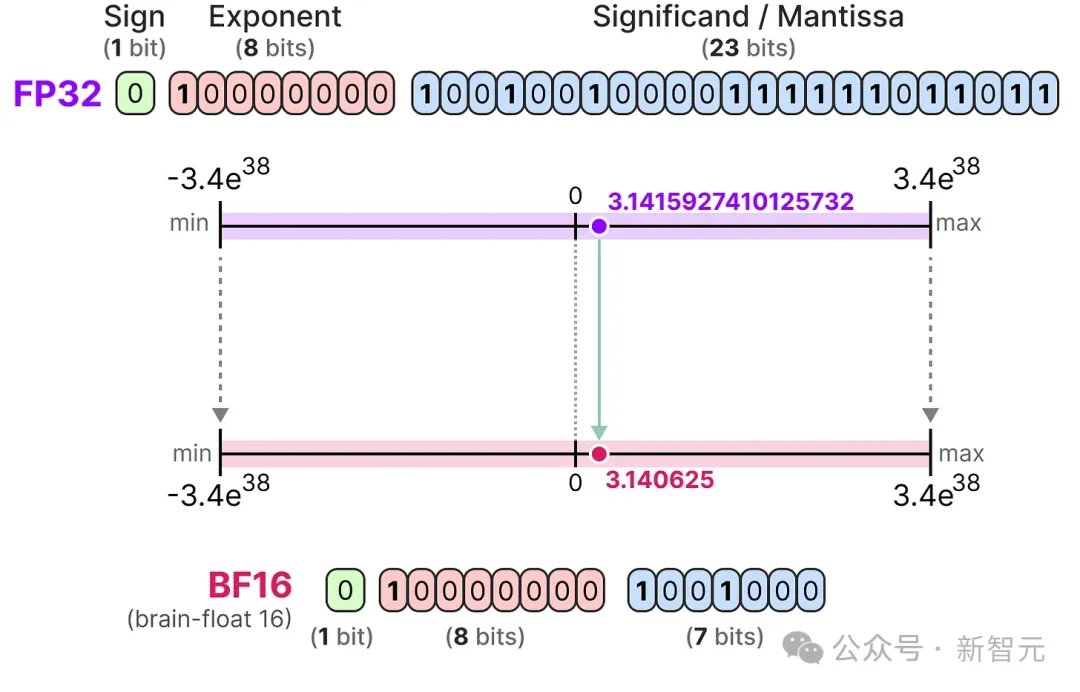
BF16使用的位数与FP16相同,但增加了指数位,因此能取到更广泛的数值范围,常用于深度学习领域。
INT8
进一步减少位数时,就更接近整数而非浮点数的表示方法。比如,从FP32到只具有8位的INT8,只有原始位数的1/4:
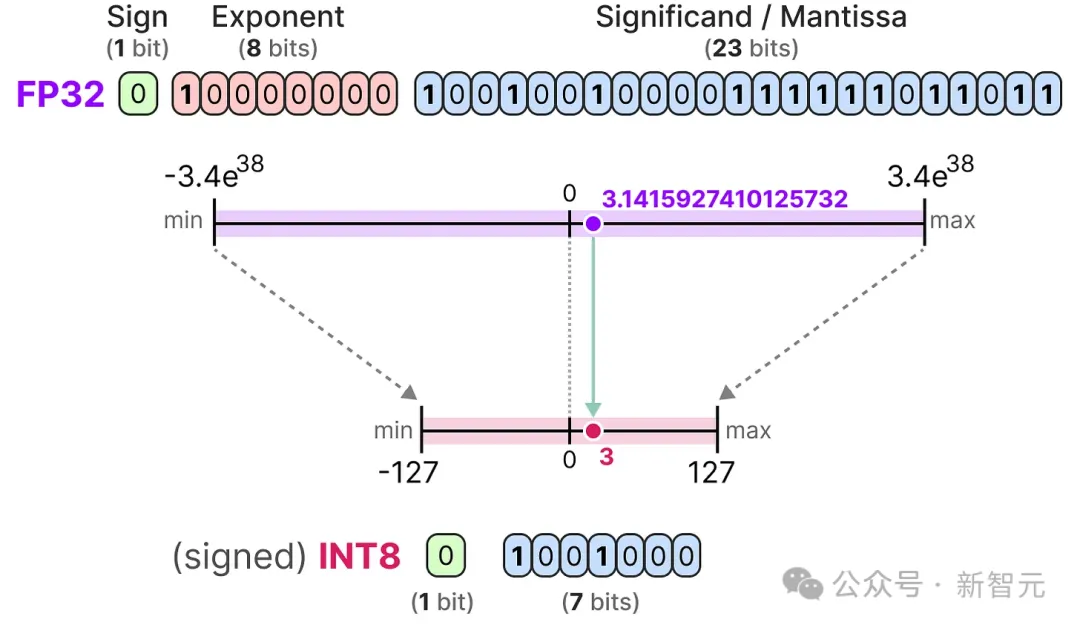
每次减少位数时,都会进行映射,将初始的FP32表示「压缩」到较少的位数中。
但在实际操作中,我们不需要将整个FP32范围[-3.4e38, 3.4e38]全部映射到INT8中。我们只需找到一种方法,将实际模型参数的数据范围映射到INT8中。
常见的压缩/映射方法可以有对称量化和非对称量化两种,都属于线性映射。
接下来将要探讨的就是从FP32到INT8的量化方法。
对称量化
在对称量化中,原始浮点值的范围被映射到量化空间中以零为中心的对称范围,量化前后的范围都以零为中点。
这意味着,原来浮点空间中的零,映射到量化空间后也恰好是零。
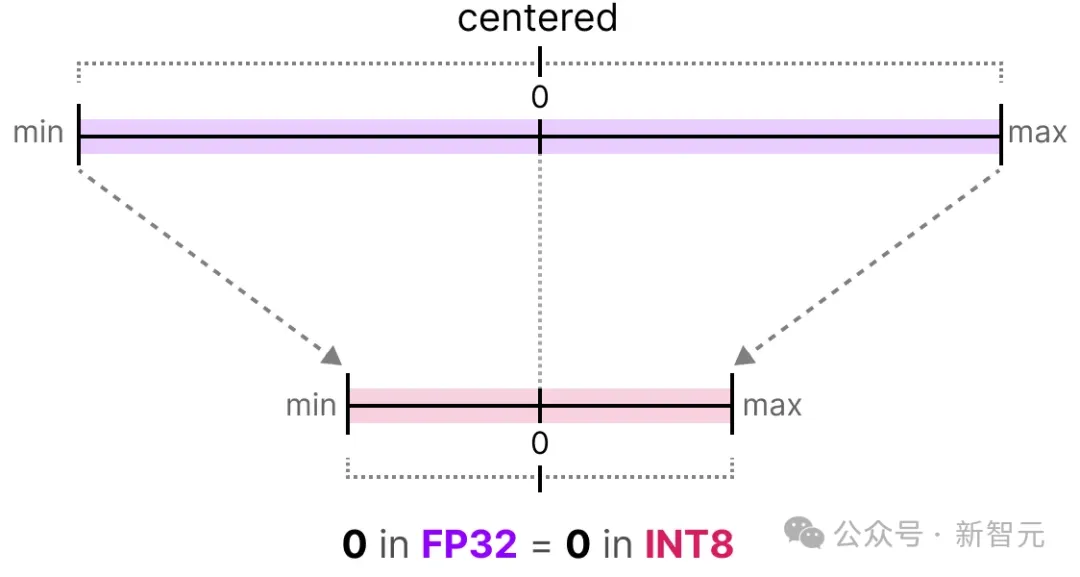
一种对称量化的典型例子是最大绝对值(absmax)量化。
给定一个数值列表,我们取其中最高的绝对值(α)作为执行线性映射的范围。
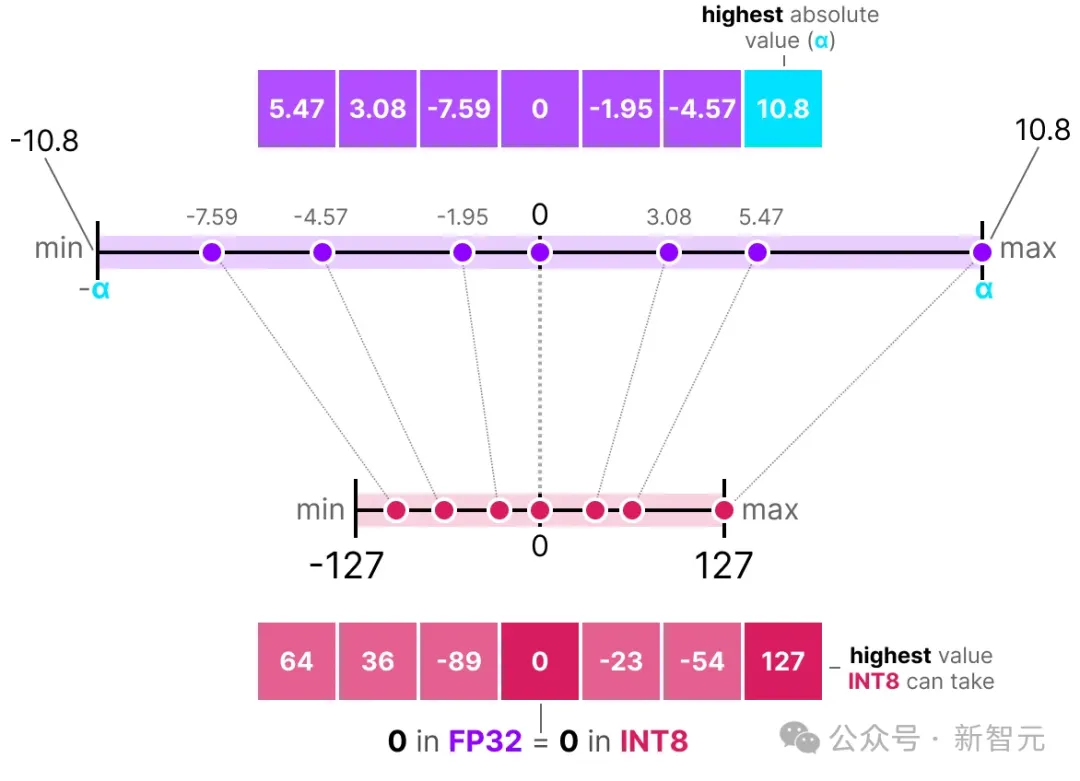
[-127, 127]表示受限范围(restricted range),未受限范围是[-128, 127],取决于量化方法
由于这是一个以零为中心的线性映射,公式很简单。
首先用以下公式计算比例因子(s):
- b是我们要量化到的字节数(8)
- α是最高的绝对值
然后,我们使用s来量化输入x:

如上图所示,最大绝对值α为10.8,将FP32映射到INT8时,即有如下公式:
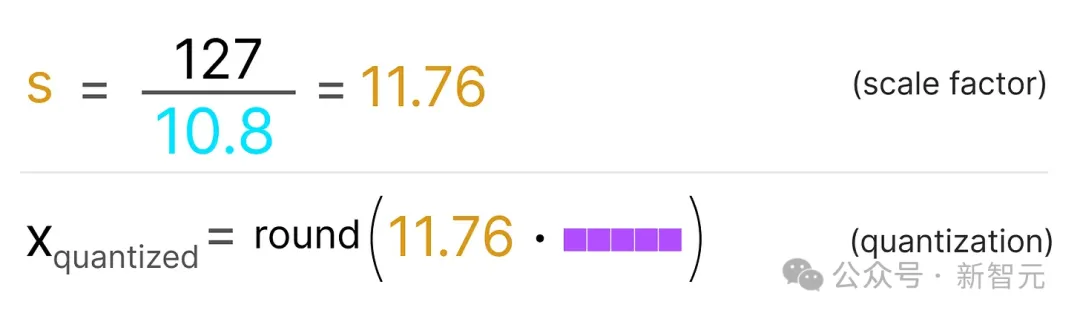
如果要恢复原始的FP32值,也可以使用先前计算的比例因子(s)来进行反量化。

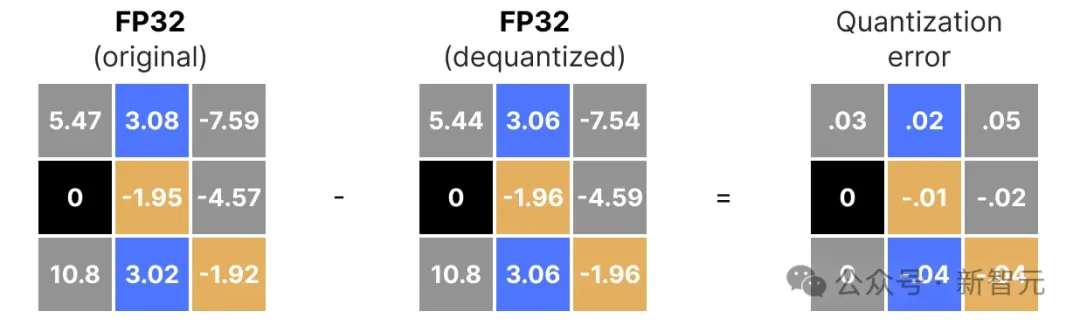
先量化,再反量化以恢复原始值,全过程如下所示:

可以看到某些值,如3.08和3.02,在量化为INT8时都是36。因此进行反量化恢复到FP32时,它们失去了一些精度并且不再可区分。
这种原始值和反量化值之间的差异被称为量化误差。通常,量化结果的位数越少,误差越大。
非对称量化
与对称量化不同,非对称量化不是以零为中心的对称。相反,它将浮点范围内的最小值(β)和最大值(α)分别映射到量化范围的最小值和最大值。
这里我们探讨的方法被称为零点量化(zero-point quantization)。
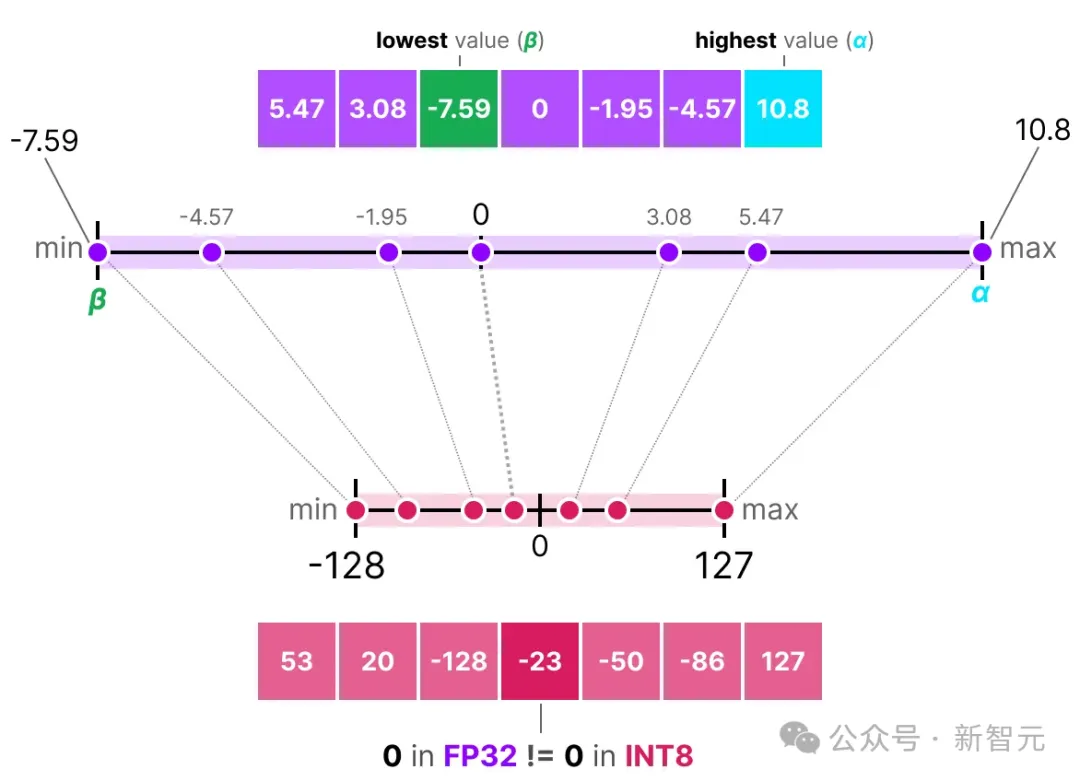
注意0的位置是如何移动的。这就是为什么它被称为非对称量化。在范围[-7.59, 10.8]中,最大值和最小值到0的距离不同。
由于零点位置的偏移,我们必须计算INT8范围内的零点才能执行线性映射。与之前一样,我们还必须计算比例因子(s),但使用INT8范围的差值[-128, 127]。

由于需要在INT8范围内计算零点(z)以移动权重,这有点复杂。
像之前一样,让我们填入公式:
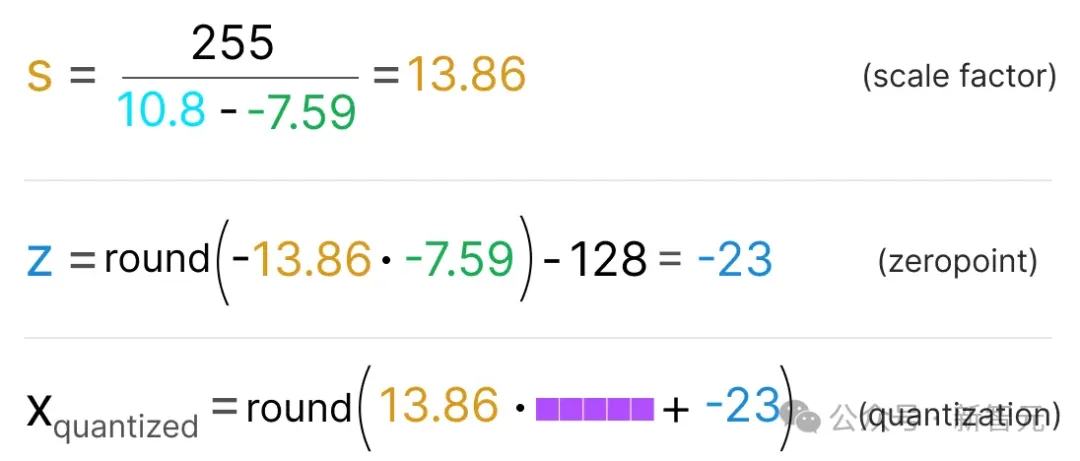
为了将量化后的值从INT8反量化回FP32,我们需要使用先前计算的比例因子(s)和零点(z)。
除此之外,反量化很简单:

当我们将对称和非对称量化并排放置时,可以快速看出两种方法之间的区别:
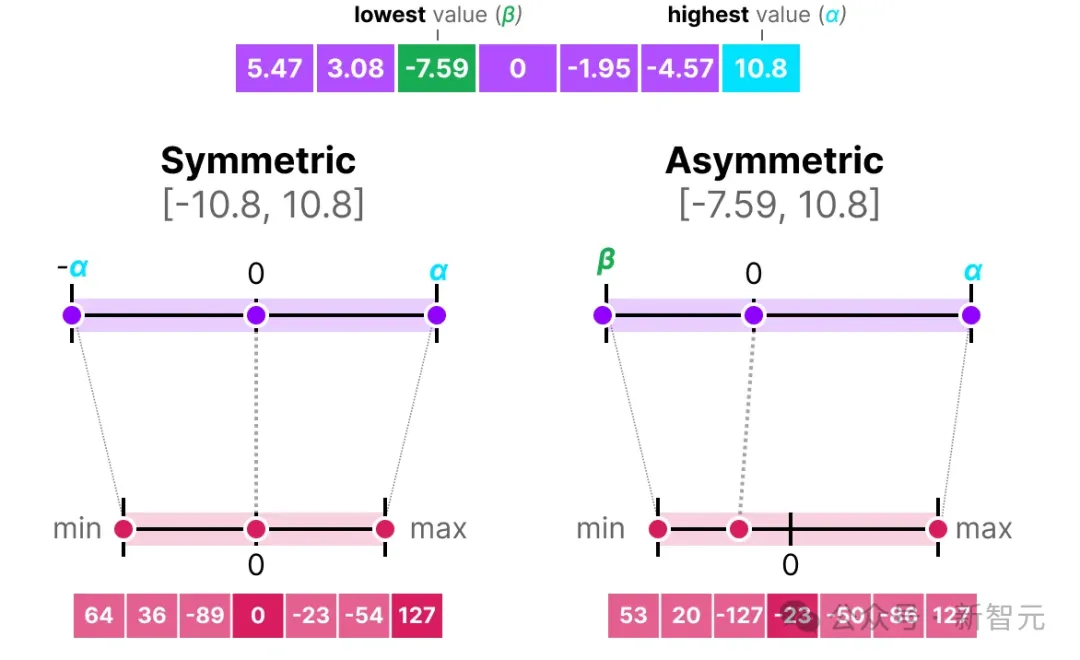
在上图中,我们能看到对称量化的零中心特性与非对称量化的偏移。
范围映射和剪裁(Clipping)
在之前的例子中,我们探讨了如何将给定向量中的值范围映射到低位表示。虽然这样可以映射整个向量值的范围,但有一个主要缺点,即异常值(outlier)。
想象一下,你有一个包含以下值的向量:

一个值比其他所有值都大得多,可以被认为是异常值。如果我们映射整个向量的范围,所有小值将被映射到相同的低位表示,并失去它们的区分度:
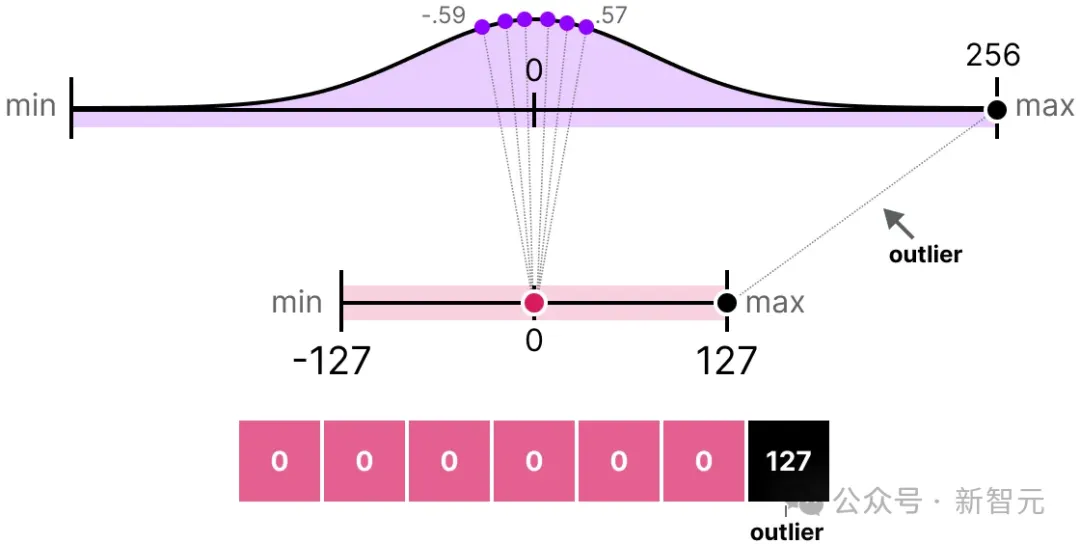
这是之前使用的absmax方法。如果不进行剪裁,非对称量化也会发生同样的情况
相反,我们可以选择剪裁某些值。剪裁是指设置原始值的不同动态范围,使所有异常值都被设为相同的值。
在下面的例子中,我们手动将动态范围设置为[-5, 5],所有超出该范围的值将被映射到-127或127,无论它们的实际值是多少:
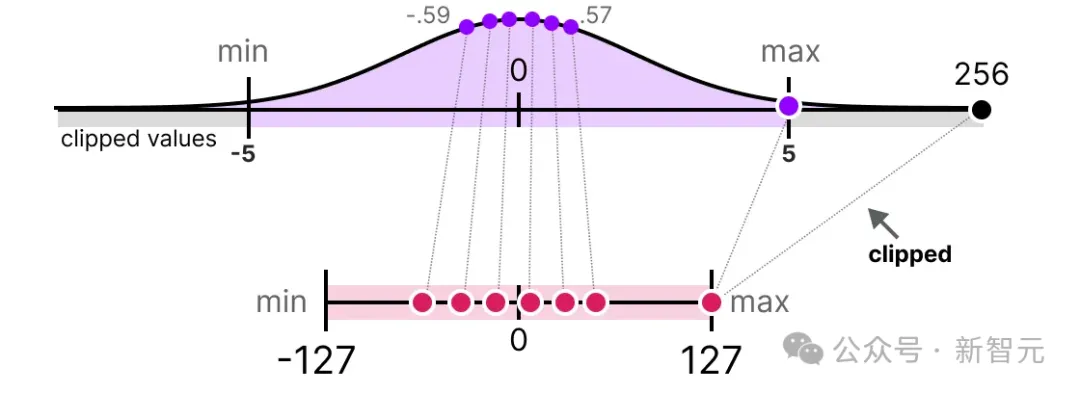
这种方法的主要优点是非异常值的量化误差显著减少。然而会导致异常值的量化误差增加。
校准(Calibration)
上面的例子中,我们随机将动态范围设置为[-5, 5],但其实应该通过「校准」过程做出决定,找到一个合适的范围,包含尽可能多的值,同时最小化量化误差。
校准步骤的具体执行对于不同类型的参数是不一样的。
权重(和偏置)
我们可以将大语言模型(LLM)的权重和偏置(weights & biases)视为静态值,因为它们在运行模型之前是已知的。例如,Llama 3的约20GB文件大部分由其权重和偏置组成。
由于偏置变量的数量(数百万)显著少于权重(数十亿),因此偏置通常保持较高精度(如INT16),而量化的主要工作集中在权重上。
对于已知的静态权重,选择范围的校准技术包括:
- 手动选择输入范围的百分位数
- 优化原始权重和量化权重之间的均方误差(MSE)
- 最小化原始值和量化值之间的熵(KL散度)

例如,选择一个百分位数,会导致类似于我们之前看到的剪裁行为。
激活值
在整个大语言模型中不断更新的输入通常被称为激活值(activations)。
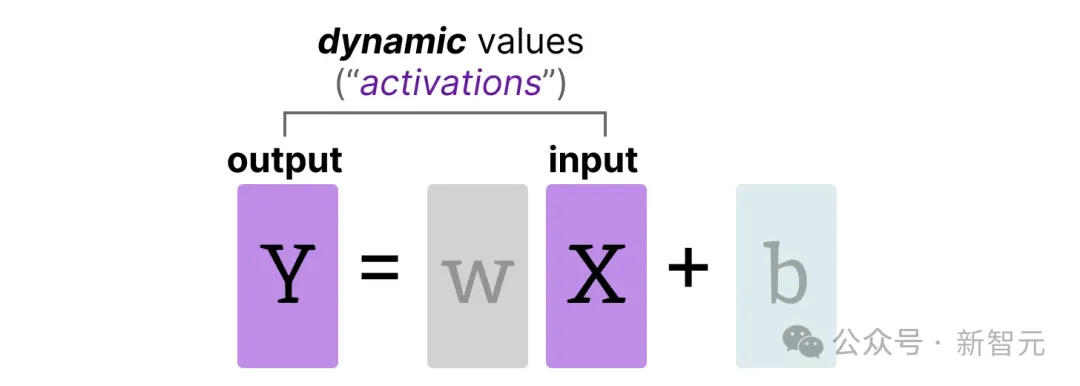
之所以被称为激活值,因为它们通常会经过一些激活函数,如sigmoid或relu
与权重不同,激活值在推理过程中随输入数据而变化,因此难以准确量化。
由于这些值在每个隐藏层之后都会更新,因此在推理阶段,只有输入数据通过模型后才能得知它们的具体数值。
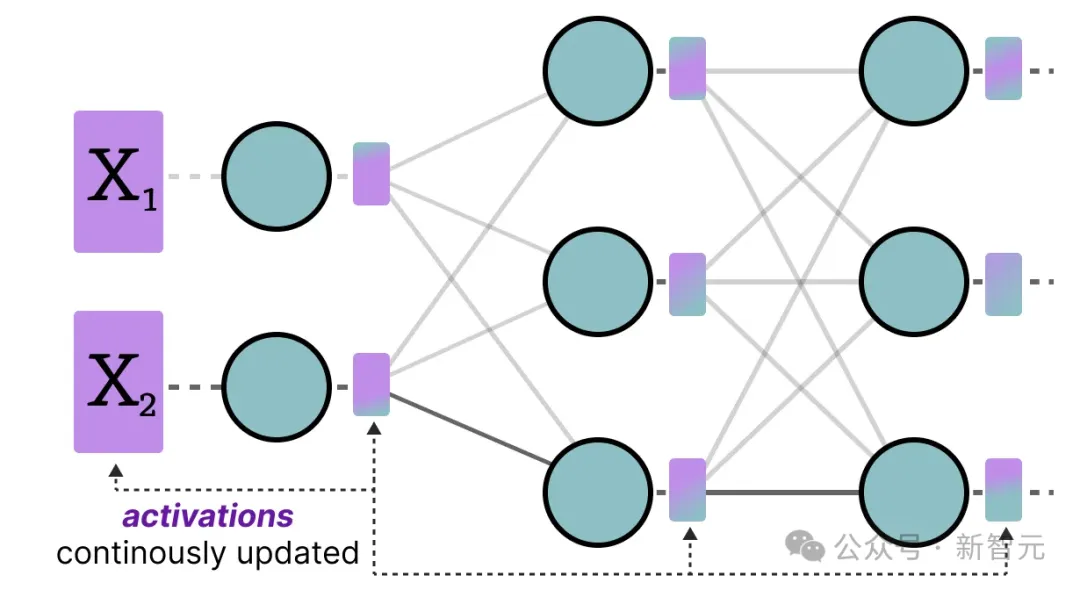
总体来说,有两种方法用于校准权重和激活值,应用于模型的不同阶段:
- 训练后量化(Post-Training Quantization,PTQ)
- 顾名思义,即训练后进行的量化
- 量化感知训练(Quantization Aware Training,QAT)
- 训练/微调期间的量化
第三部分:训练后量化(PTQ)
训练后量化(PTQ)是最流行的量化技术之一。它是在模型训练完成后,对模型的参数(包括权重和激活值)进行量化。
权重的量化可以采用对称量化或非对称量化的方法。
然而,激活值的量化需要经过推理阶段来获取其潜在分布,因为我们事先并不知道它们的范围。
激活值的量化有两种形式:
- 动态量化(dynamic quantization)
- 静态量化(static quantization)
动态量化
数据通过隐藏层后,其激活值会被收集,比较出每一层的最大值(α)和最小值(β):
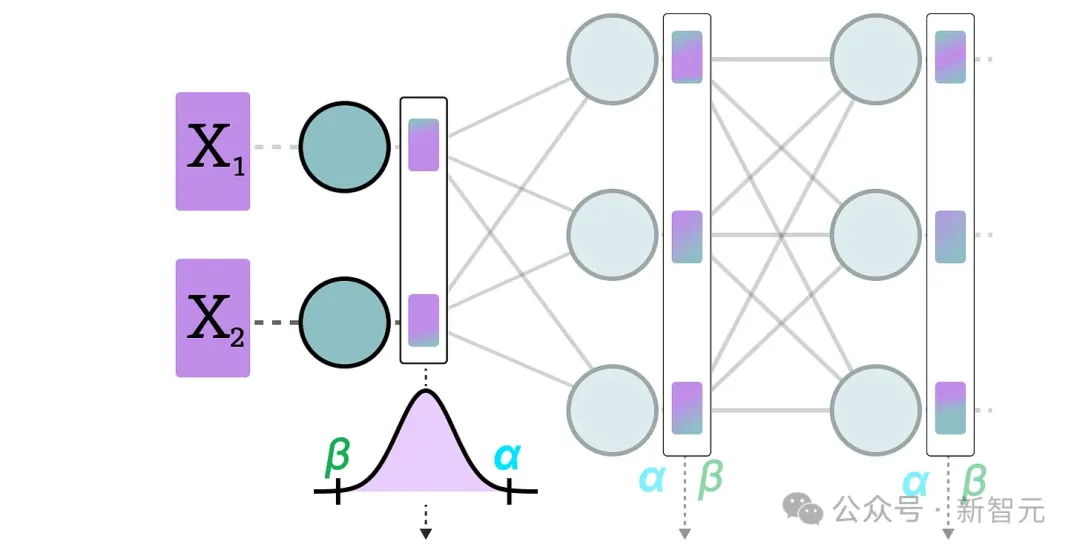
然后利用这些激活值的分布来计算量化输出所需的零点(zeropoint,z)和比例因子(scale factor,s)值:
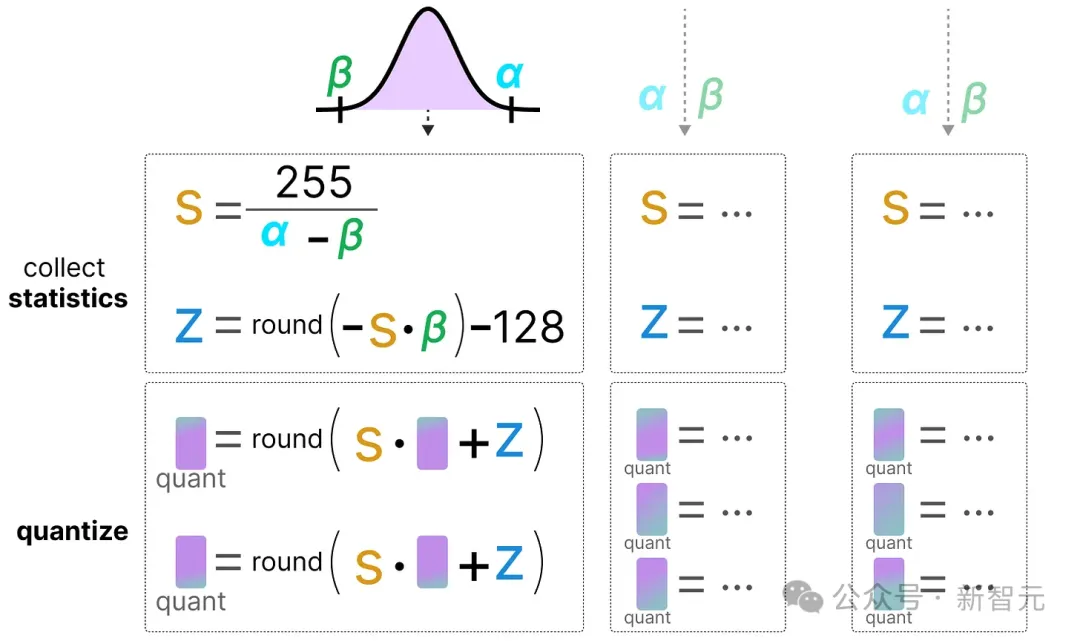
每次数据通过新的网络层时,这个过程都会重复。因此,每一层都有其独立的z和s值,从而使用不同的量化方案。
静态量化
与动态量化不同,静态量化并不是在推理过程中计算零点(zeropoint,z)和比例因子(scale factor,s),而是在推理之前计算这些值。
为了找到这些值,我们会使用一个校准数据集,并将其输入模型以收集这些潜在的激活值分布。
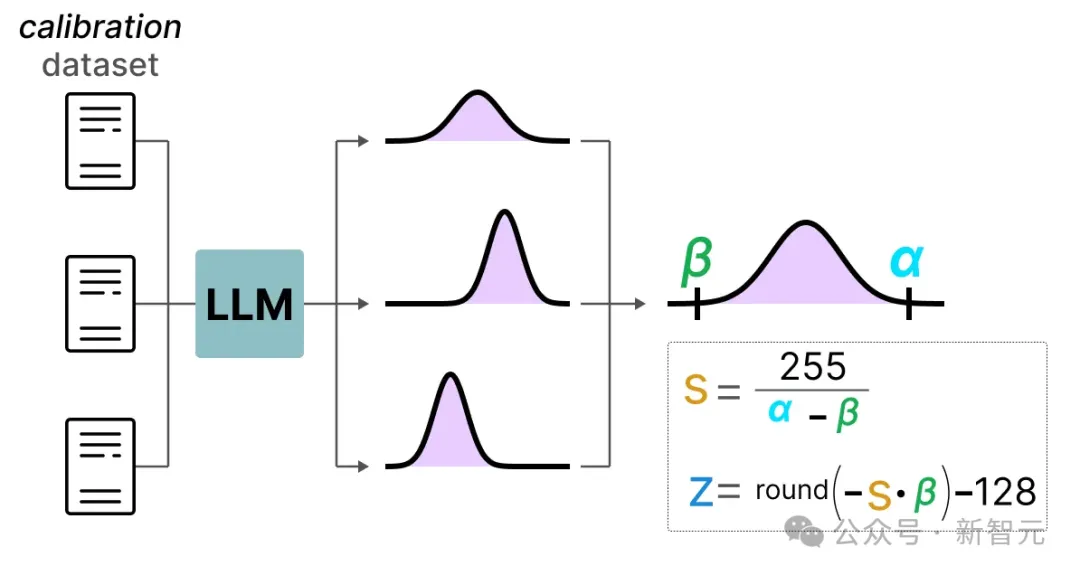
收集到这些分布之后,就可以计算出在推理过程中进行量化所需的s和z值。
在实际推理时,不会重新计算s和z值,而是在所有激活中全局使用它们来对其进行量化。
总体来说,动态量化为每个隐藏层计算s和z值,往往更准确。然而,这可能会增加计算时间,因为这些值需要在每次推理时计算。
相反,静态量化虽然不如动态量化准确,但速度更快,因为它已经预先知道用于量化的s和z值。
4-bit量化领域
低于8-bit的量化一直是一个挑战,因为每减少一位,量化误差就会增加。幸运的是,有几种巧妙的方法可以将位数减少到6、4,甚至2-bit(尽管通常不建议将位数降到低于4-bit)。
我们将探讨在HuggingFace上常见的两种方法:
- GPTQ(全模型在GPU上运行)
- GGUF(可能将层卸载到CPU上)
GPTQ
GPTQ可以说是实际应用中最著名的4-bit量化方法之一。
它使用非对称量化,并逐层进行处理,每层独立处理后再继续处理下一层:
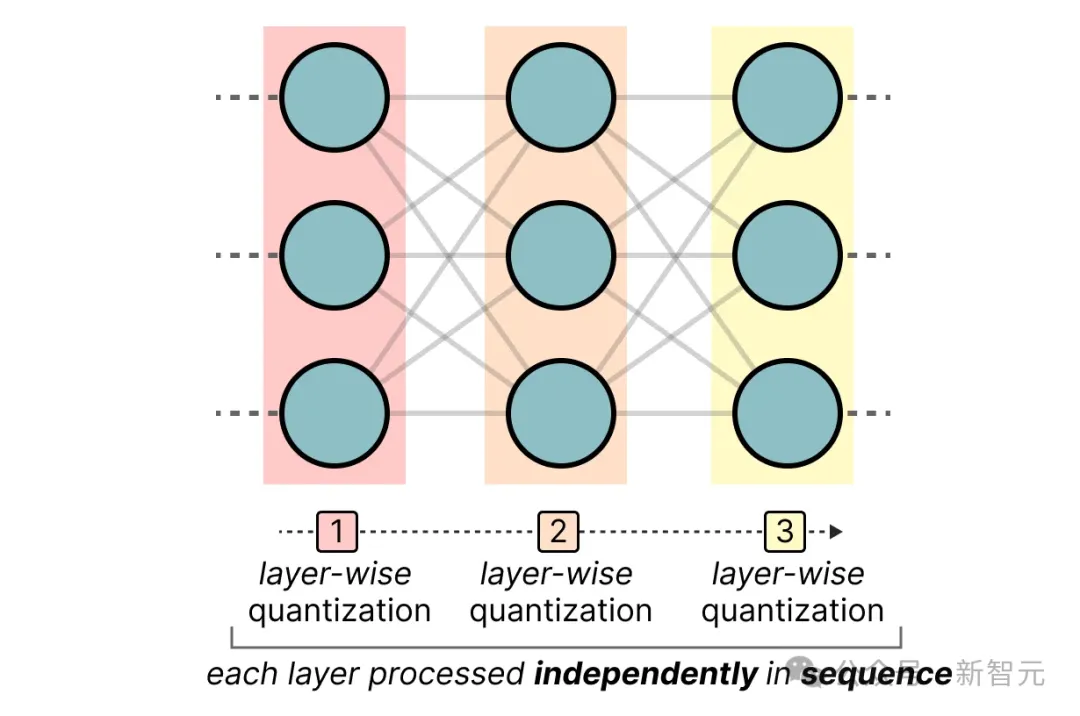
在这个逐层量化过程中,它首先将层的权重转换为逆Hessian矩阵。逆Hessian矩阵是模型损失函数的二阶导数,表示模型输出对每个权重变化的敏感性。
简单来说,它本质上展示了每个层中权重的重要性(逆重要性)。
Hessian矩阵中较小值的权重更为重要,因为这些权重的微小变化可能导致模型性能的显著变化。
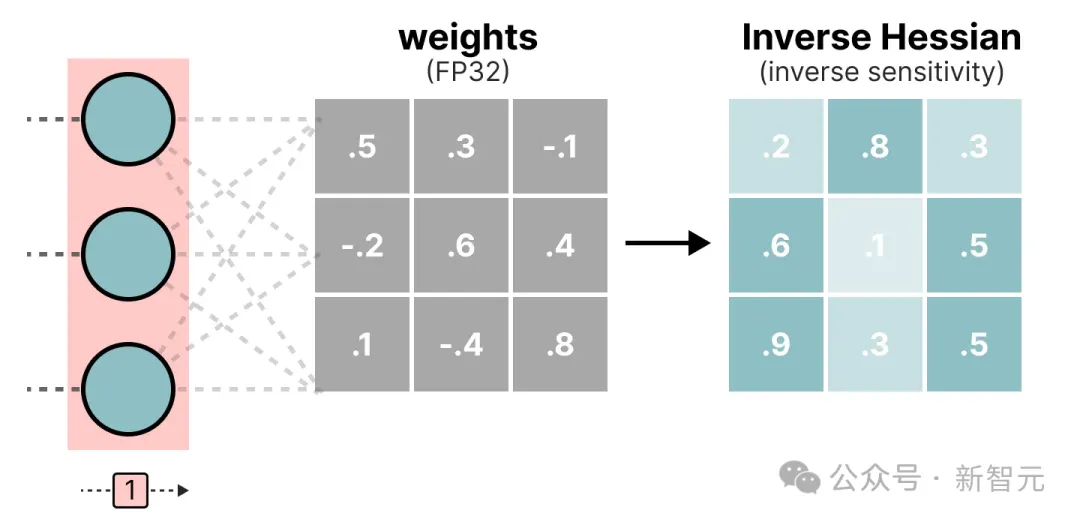
在逆Hessian矩阵中,较低的值表示更「重要」的权重
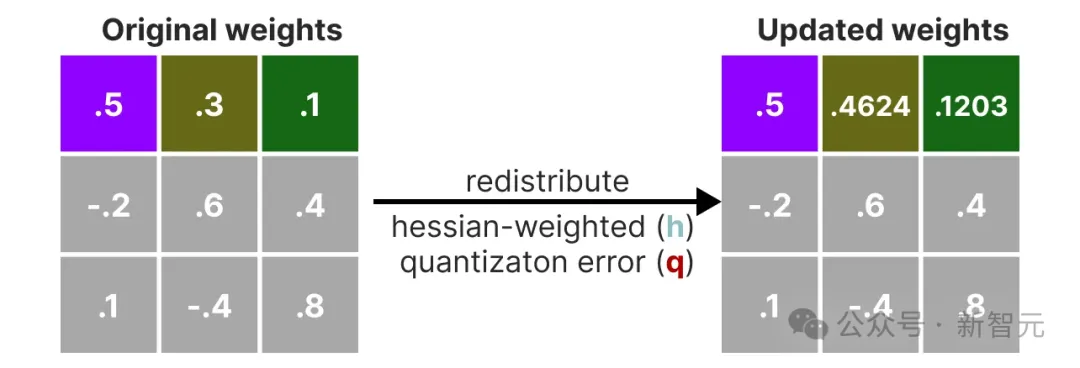
接下来,我们量化并反量化权重矩阵的第一行:

这一过程使我们能够计算量化误差(q),我们可以使用之前计算的逆Hessian值(h_1)来加权这个量化误差。
本质上,我们是在基于权重的重要性创建加权量化误差:

接下来,我们将这个加权量化误差重新分配到该行的其他权重上。这有助于保持网络的整体功能和输出。
例如,如果对第二个权重(即x_2=0.3)进行此操作,我们会将量化误差(q)乘以第二个权重的逆Hessian(h_2)加上去:

接下来,继续对给定行中的第三个权重进行相同的操作:
重复这个重新分配加权量化误差q的过程,直到所有值都被量化。
这个方法所以有效,是因为权重通常是相互关联的。因此,当一个权重有量化误差时,相关的权重会通过逆Hessian进行相应的更新。
GGUF
虽然GPTQ是一种很好的在GPU上运行整个大语言模型(LLM)的量化方法,但如果没有相应的硬件条件,也可以通过GGUF将LLM的任意层卸载到CPU上。
相当于同时用CPU和GPU运行模型,以弥补显存(VRAM)不足的情况。
量化方法GGUF经常更新,而且依赖于具体的量化位数,但基本原理如下。
首先,给定层的权重被分成「超级块」,每个「超级块」包含一组「子块」。从这些「子块」中,我们计算出比例因子(s)和α值:
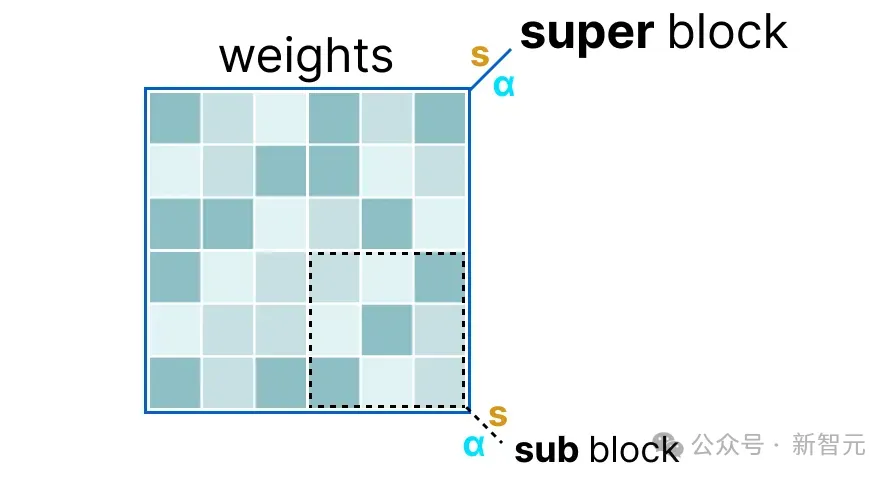
为了量化给定的「子块」,可以使用之前提到的absmax量化,将给定的权重乘以比例因子(s_sub):

比例因子s_sub是使用「子块」中的信息计算的,但用「超级块」中的信息s_super进行量化:

总而言之,这种以块为单位的量化使用「超级块」的比例因子(s_super)来量化「子块」的比例因子(s_sub)。
每个比例因子的量化级别可能不同,「超级块」的比例因子通常比「子块」有更高的精度。
为了说明这一点,让我们探讨几个量化级别(2-bit、4-bit和6-bit):
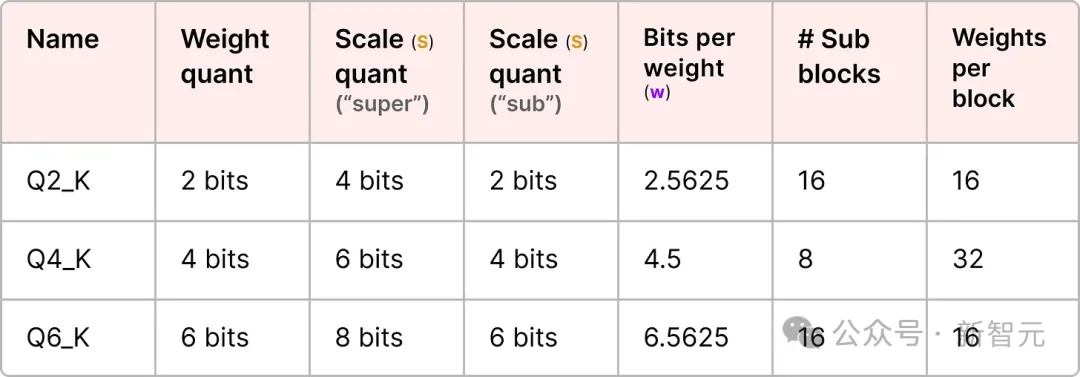
根据量化类型,还需要一个额外的最小值(m)来调整零点,这些与比例因子(s)一样被量化
第四部分:量化感知训练(QAT)
第三部分讲述了如何在训练后对模型进行量化。这种方法的缺点在于,没有考虑到实际的训练过程。
这就是量化感知训练(QAT)派上用场的地方。与训练后量化(PTQ)不同,QAT的目标是在训练中学习量化过程。
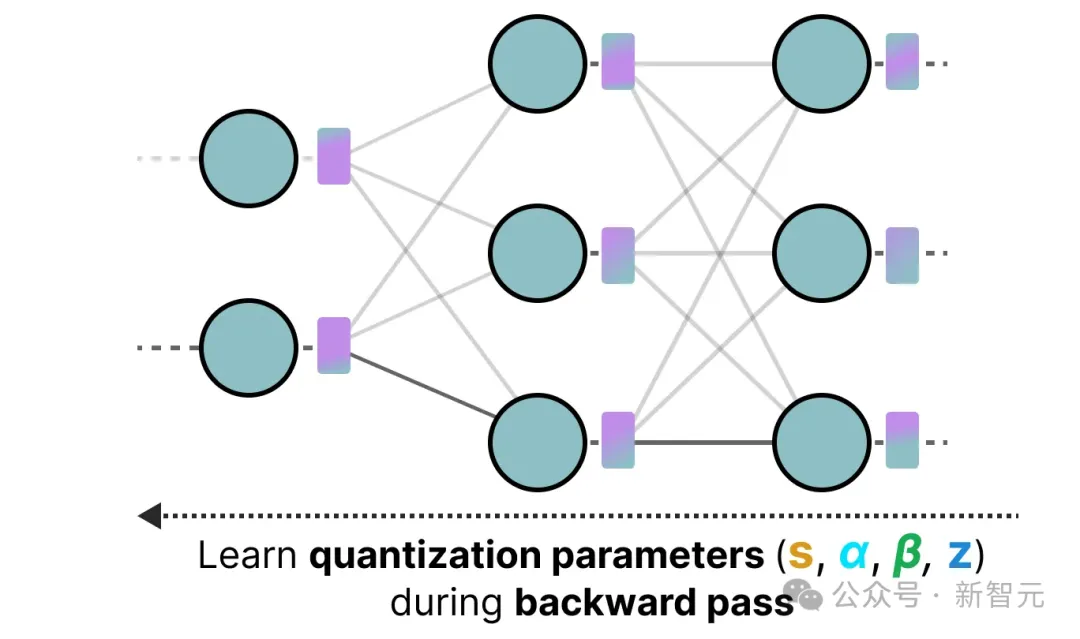
QAT往往比PTQ更准确,因为在训练过程中已经考虑了量化。其工作原理如下:
在训练过程中,引入了所谓的「假」量化。比如先将权重量化为INT4,然后再反量化回FP32:

这一过程让模型在训练阶段进行损失计算和权重更新时,就已经考虑到了量化误差。
如下图所示,QAT尝试探索「宽」极小值情况下的损失值,以减少量化误差,因为「窄」极小值往往会导致更大的量化误差。
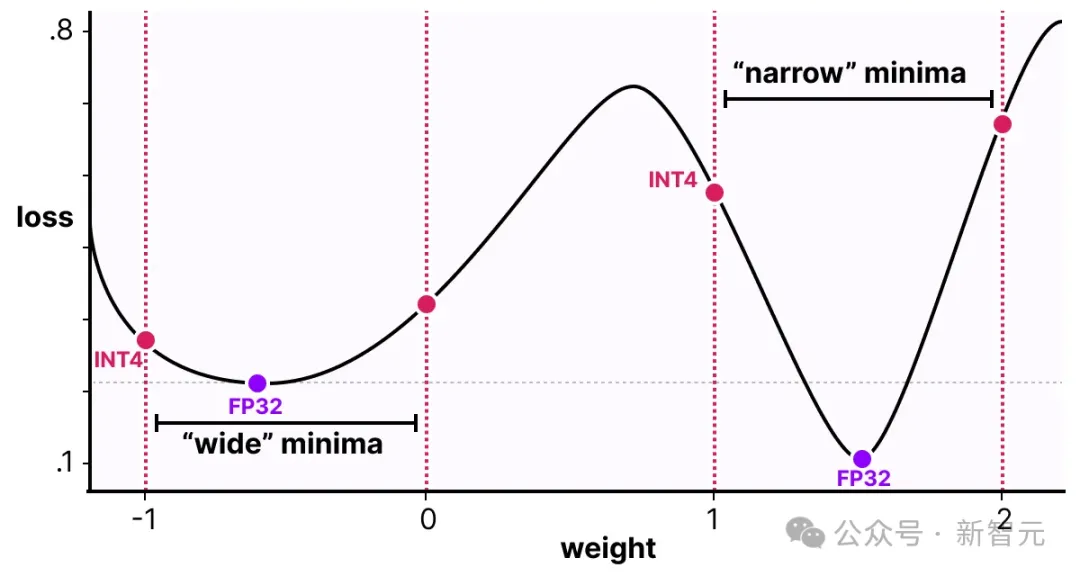
假设在反向传播过程中没有考虑量化,梯度下降过程就会选择损失值最小的权重。然而,如果它处于「窄」极小值中,那将引入更大的量化误差。
相反,如果我们考虑量化,将在「宽」极小值中选择一个不同的更新权重,其量化误差要小得多。
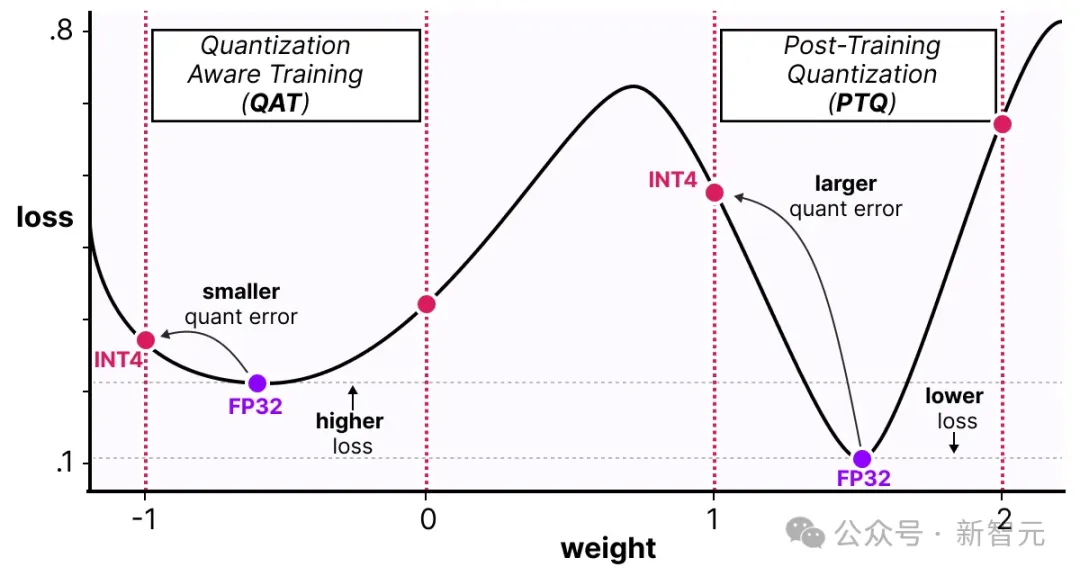
因此,尽管PTQ方法在高精度(例如FP32)有较低的损失值,但QAT在低精度(例如INT4)下损失值也很低,这是我们所追求的。
1-bit时代:BitNet
之前我们看到,将量化精度降低到4-bit已经相当小了,但如果我们进一步降低呢?
这就是BitNet的用武之地,它将模型的权重表示为单个比特,即-1或1,通过将量化过程直接注入到Transformer架构中来实现这一点。
Transformer架构是大多数LLM的基础,由涉及线性层的计算组成:
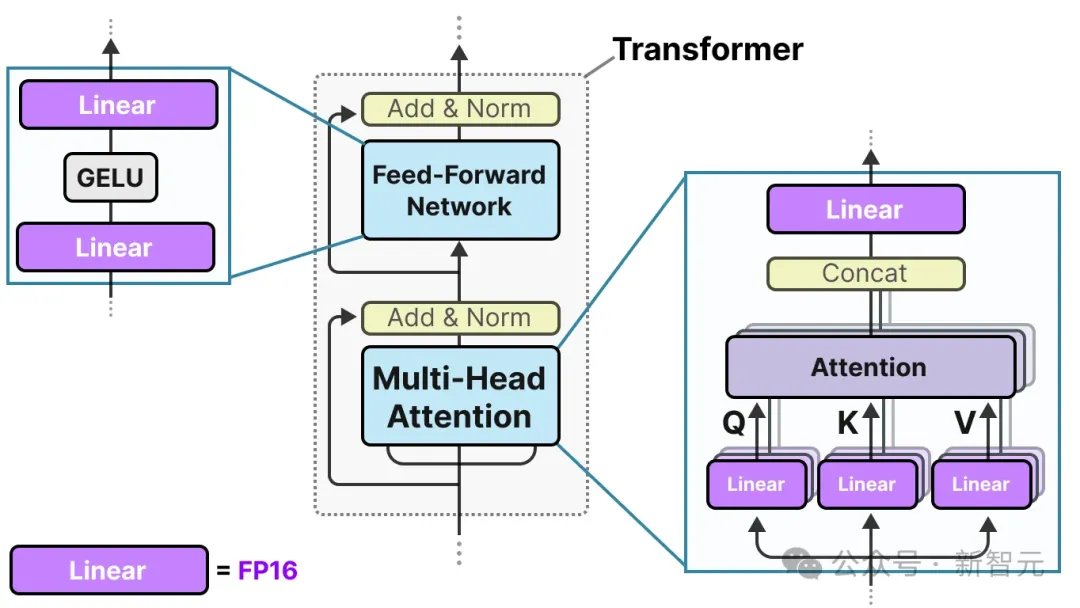
这些线性层通常以更高的精度表示,如FP16,而且是大多数权重所在的位置。
BitNet用BitLinear层替换了这些线性层:
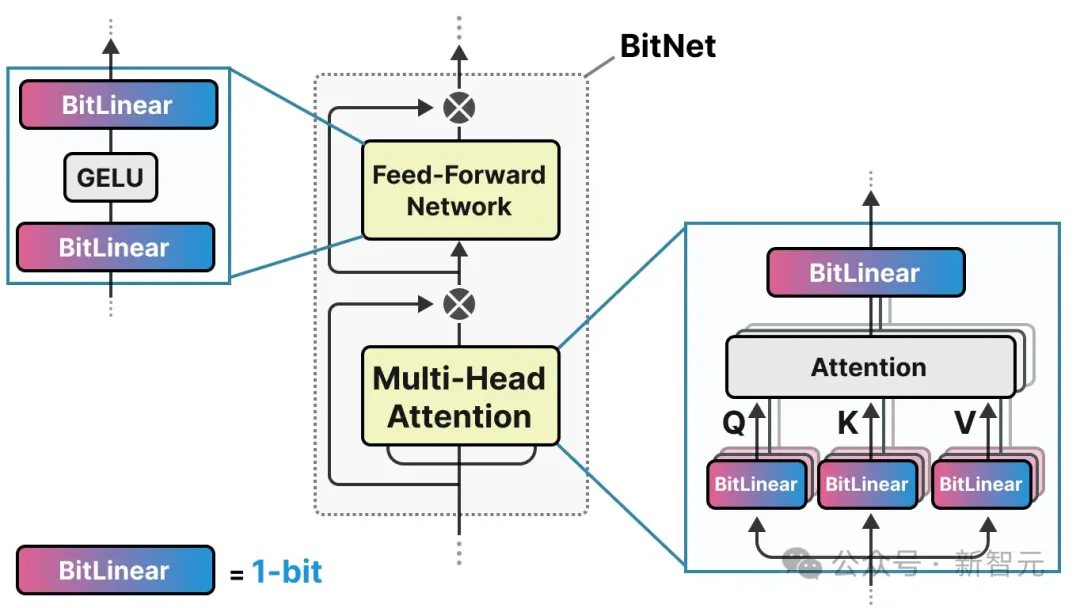
BitLinear层的工作原理与普通线性层相同,用权重乘以激活值来计算输出。
但不同的是,BitLinear层仅用1位表示模型的权重,使用INT8表示激活值:
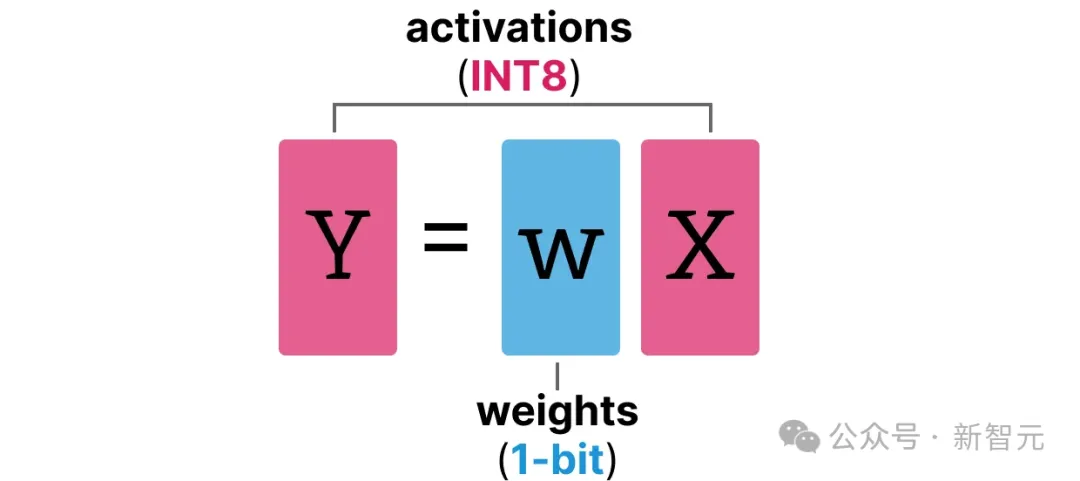
BitLinear层像量化感知训练(QAT)一样,在训练期间执行一种「假」量化,以分析权重和激活值的量化效果:
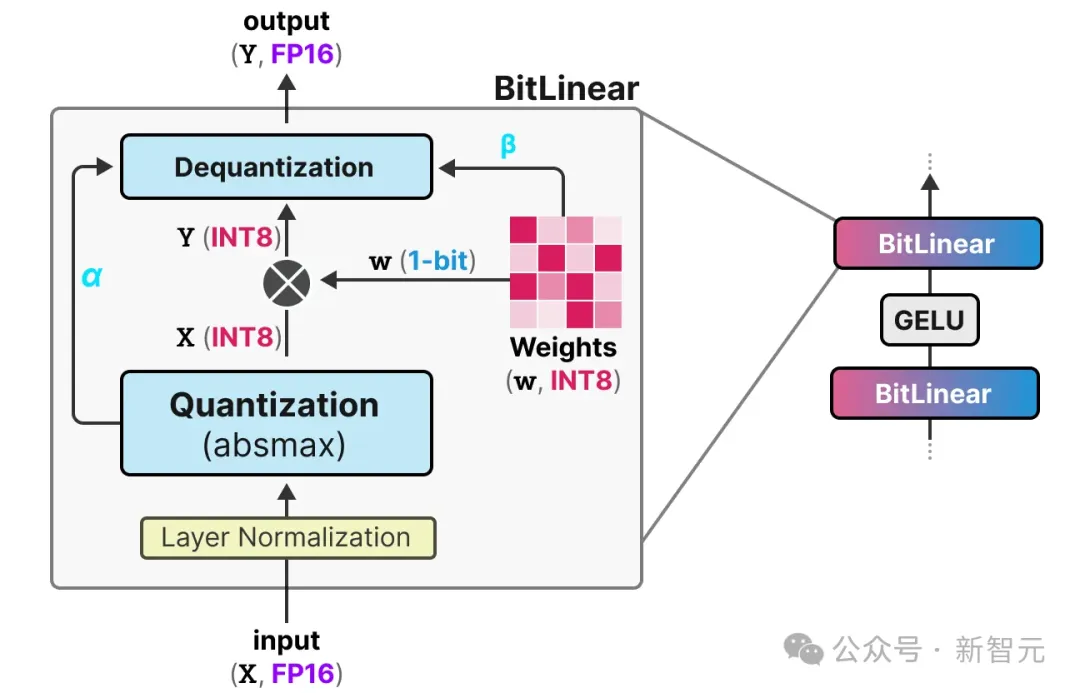
让我们一步步地了解BitLinear。
权重量化
在训练过程中,权重以INT8存储,然后使用一种称为符号函数(signum function)的基本策略将其量化为1位。
本质上,它将权重的分布移动至以0为中心,然后将所有小于0的值分配为-1,将所有大于0的值分配为1:
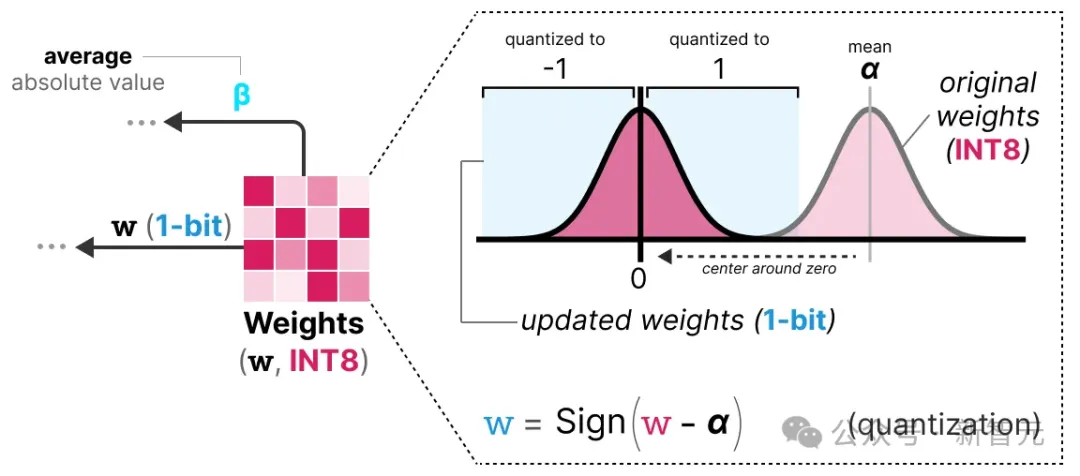
此外,它还跟踪一个值β(平均绝对值),我们将在之后的反量化过程中使用。
激活值量化
为了量化激活值,BitLinear使最大绝对值方法(absmax)将激活值从FP16转换为INT8,因为它们需要以较高的精度进行矩阵乘法(×)。

此外,它还跟踪一个值α(最大绝对值),我们将在之后的反量化过程中使用。
反量化
我们跟踪了α(激活值的最大绝对值)和β(权重的平均绝对值),这些值将帮助我们将激活值反量化回FP16。
输出激活值使用{α, γ}重新缩放,以将其反量化到原始精度:
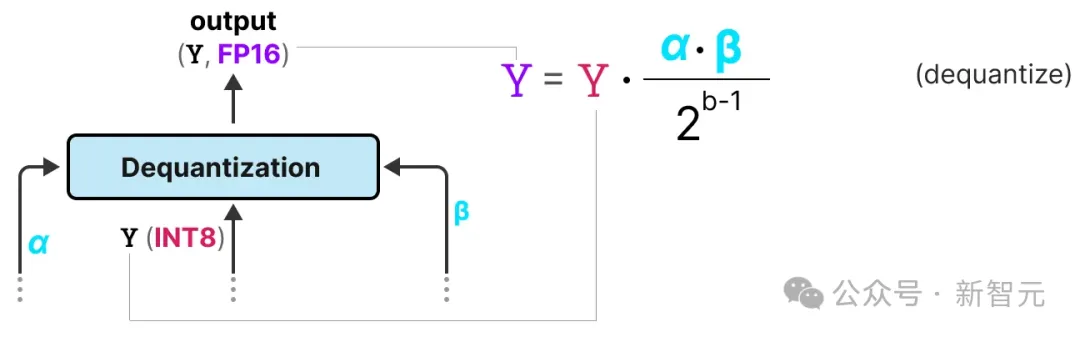
这个过程相对简单,并且允许模型仅用两个值表示,即-1或1。
通过这种方法,作者观察到,随着模型规模的增长,1位训练和FP16训练之间的性能差距越来越小。
然而,这仅适用于较大的模型(>30B参数),较小模型之间的差距仍然很大。
所有LLM都是1.58位
为了改善之前提到的扩展性问题,BitNet 1.58b被引入。
在这种新方法中,模型的每个权重不仅可以是-1或1,还可以取0,使每个变量成为三元值(ternary)。
有趣的是,仅仅是添加0这个简单的操作,就大大改进了BitNet,加速了计算过程。
0的力量
为什么添加0是一个重大改进呢?
这与矩阵乘法有关!
首先,让我们探讨一下矩阵乘法的基本工作原理。
当计算输出时,我们将权重矩阵与输入向量相乘。下面是权重矩阵的第一层的第一行乘法的可视化:

这种乘法涉及两个动作,将单个权重与输入相乘,然后将它们全部相加。
相比之下,BitNet 1.58b设法避免了乘法的动作,因为三值权重本质上告诉你以下内容:
- 1:我想加上这个值
- 0:我不想要这个值
- -1:我想减去这个值
因此,如果你的权重被量化到1.58 bit,你只需要执行加法:
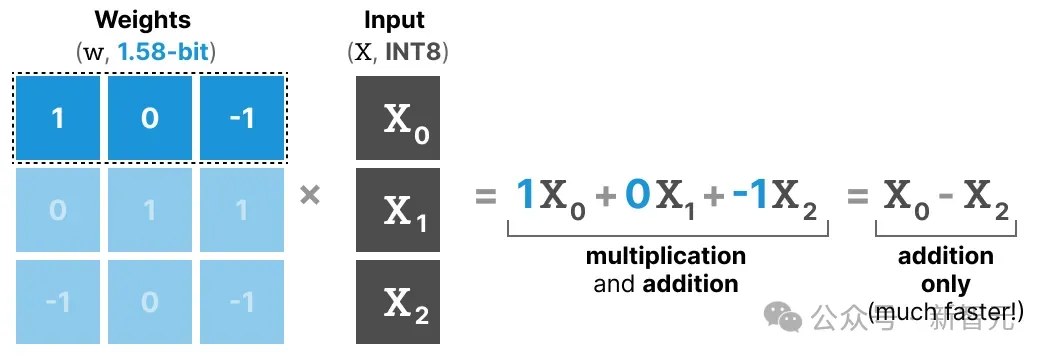
这不仅可以显著加快计算速度,还允许特征过滤。
将给定的权重设置为0就相当于忽略了这个输入,而不是像1-bit那样,表示加上或减去输入值。
量化
为了执行权重量化,BitNet 1.58b使用平均绝对值量化(absmean),这是我们之前见过的最大绝对值量化(absmax)的变体。
它只是压缩权重的分布并使用绝对均值(α)来量化值。然后将它们四舍五入为-1、0或1:
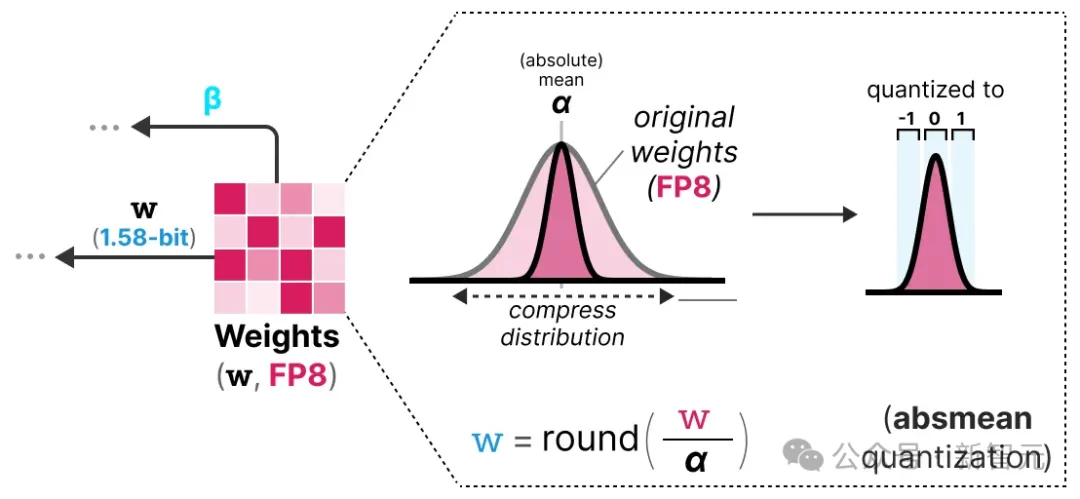
与BitNet相比,激活值量化是相同的,除了一个方面:不是将激活值缩放到范围[0, 2ᵇ⁻¹],而是使用最大绝对值方法缩放到[-2ᵇ⁻¹, 2ᵇ⁻¹]。
总结一下,1.58-bit量化主要涉及两个技巧:
- 添加0以创建三值表示[-1, 0, 1]
- 权重的绝对均值量化
BitNet论文中有这样的结论:「13B BitNet b1.58在延迟、内存使用和能耗方面比3B FP16 LLM更高效。」

论文地址:https://arxiv.org/abs/2402.17764
由于只有1.58个计算效率高的bit,我们得到了轻量级模型。