多层感知器 (Multi-Layer Perceptrons,MLP) ,也被称为全连接前馈神经网络,是当今深度学习模型的基本组成部分。MLP 的重要性无论怎样强调都不为过,因为它是机器学习中用于逼近非线性函数的默认方法。
然而,MLP 也存在某些局限性,例如难以解释学习到的表示,以及难以灵活地扩展网络规模。
KAN(Kolmogorov–Arnold Networks)的出现,为传统 MLP 提供了一种创新的替代方案。该方法在准确性和可解释性方面优于 MLP,而且,它能以非常少的参数量胜过以更大参数量运行的 MLP。
那么,问题来了,KAN 、MLP 到底该选哪一种?有人支持 MLP,因为 KAN 只是一个普通的 MLP,根本替代不了,但也有人则认为 KAN 更胜一筹,而当前对两者的比较也是局限在不同参数或 FLOP 下进行的,实验结果并不公平。
为了探究 KAN 的潜力,有必要在公平的设置下全面比较 KAN 和 MLP 了。
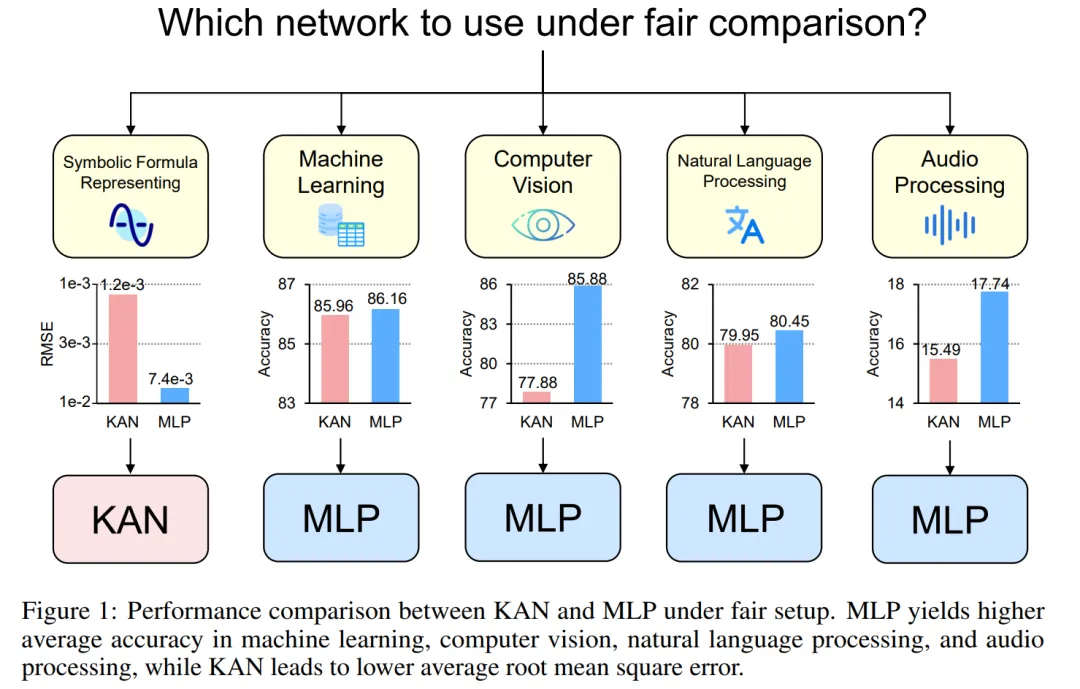
为此,来自新加坡国立大学的研究者在控制了 KAN 和 MLP 的参数或 FLOP 的情况下,在不同领域的任务中对它们进行训练和评估,包括符号公式表示、机器学习、计算机视觉、NLP 和音频处理。在这些公平的设置下,他们发现 KAN 仅在符号公式表示任务中优于 MLP,而 MLP 通常在其他任务中优于 KAN。

- 论文地址:https://arxiv.org/pdf/2407.16674
- 项目链接:https://github.com/yu-rp/KANbeFair
- 论文标题:KAN or MLP: A Fairer Comparison
作者进一步发现,KAN 在符号公式表示方面的优势源于其使用的 B - 样条激活函数。最初,MLP 的整体性能落后于 KAN,但在用 B - 样条代替 MLP 的激活函数后,其性能达到甚至超过了 KAN。但是,B - 样条无法进一步提高 MLP 在其他任务(如计算机视觉)上的性能。
作者还发现,KAN 在连续学习任务中的表现实际上并不比 MLP 好。最初的 KAN 论文使用一系列一维函数比较了 KAN 和 MLP 在连续学习任务中的表现,其中每个后续函数都是前一个函数沿数轴的平移。而本文比较了 KAN 和 MLP 在更标准的类递增持续学习设置中的表现。在固定的训练迭代条件下,他们发现 KAN 的遗忘问题比 MLP 更严重。
KAN、MLP 简单介绍
KAN 有两个分支,第一个分支是 B 样条分支,另一个分支是 shortcut 分支,即非线性激活与线性变换连接在一起。在官方实现中,shortcut 分支是一个 SiLU 函数,后面跟着一个线性变换。令 x 表示一个样本的特征向量。那么,KAN 样条分支的前向方程可以写成:
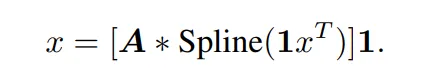
在原始 KAN 架构中,样条函数被选择为 B 样条函数。每个 B 样条函数的参数与其他网络参数一起学习。
相应的,单层 MLP 的前向方程可以表示为:
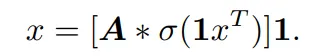
该公式与 KAN 中的 B 样条分支公式具有相同的形式,只是在非线性函数中有所不同。因此,抛开原论文对 KAN 结构的解读,KAN 也可以看作是一种全连接层。
因而,KAN 和普通 MLP 的区别主要有两点:
- 激活函数不同。通常 MLP 中的激活函数包括 ReLU、GELU 等,没有可学习的参数,对所有输入元素都是统一的,而在 KAN 中,激活函数是样条函数,有可学习的参数,并且对于每个输入元素都是不一样的。
- 线性和非线性运算的顺序。一般来说,研究者会把 MLP 概念化为先进行线性变换,再进行非线性变换,而 KAN 其实是先进行非线性变换,再进行线性变换。但在某种程度上,将 MLP 中的全连接层描述为先非线性,后线性也是可行的。
通过比较 KAN 和 MLP,该研究认为两者之间的差异主要是激活函数。因而,他们假设激活函数的差异使得 KAN 和 MLP 适用于不同的任务,从而导致两个模型在功能上存在差异。为了验证这一假设,研究者比较了 KAN 和 MLP 在不同任务上的表现,并描述了每个模型适合的任务。为了确保公平比较,该研究首先推导出了计算 KAN 和 MLP 参数数量和 FLOP 的公式。实验过程控制相同数量的参数或 FLOP 来比较 KAN 和 MLP 的性能。
KAN 和 MLP 的参数数量及FLOP
控制参数数量
KAN 中可学习的参数包括 B 样条控制点、shortcut 权重、B 样条权重和偏置项。总的可学习参数数量为:
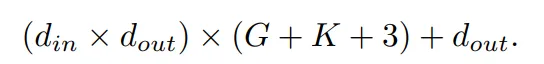
其中, d_in 和 d_out 表示神经网络层的输入和输出维度,K 表示样条的阶数,它与官方 nn.Module KANLayer 的参数 k 相对应,它是样条函数中多项式基础的阶数。G 表示样条间隔数,它对应于官方 nn.Module KANLayer 的 num 参数。它是填充前 B 样条曲线的间隔数。在填充之前,它等于控制点的数量 - 1。在填充后,应该有 (K +G) 个有效控制点。
相应的,一个 MLP 层的可学习参数是:
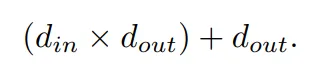
KAN 和 MLP 的 FLOP
在作者的评估中,任何算术操作的 FLOP 被考虑为 1,而布尔操作的 FLOP 被考虑为 0。De Boor-Cox 算法中的 0 阶操作可以转换为一系列布尔操作,这些操作不需要进行浮点运算。因此,从理论上讲,其 FLOP 为 0。这与官方 KAN 实现不同,在官方实现中,它将布尔数据转换回浮点数据来进行操作。
在作者的评估中,FLOP 是针对一个样本计算的。官方 KAN 代码中使用 De Boor-Cox 迭代公式实现的 B 样条 FLOP 为:
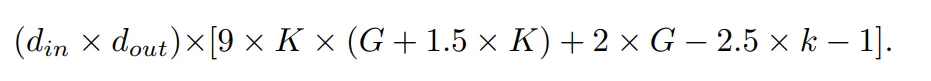
连同 shortcut 路径的 FLOP 以及合并两个分支的 FLOP,一个 KAN 层的总 FLOP 是:
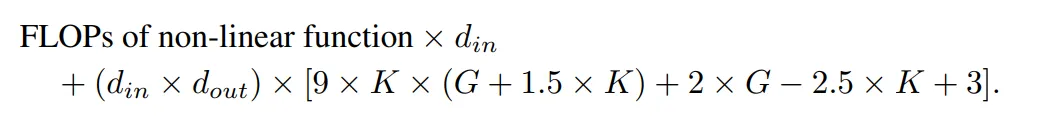
相应的,一个 MLP 层的 FLOP 为:

具有相同输入维度和输出维度的 KAN 层与 MLP 层之间的 FLOP 差异可以表示为:
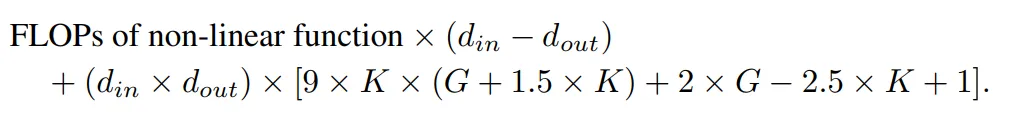
如果 MLP 也首先进行非线性操作,那么首项将为零。
实验
作者的目标是,在参数数量或 FLOP 相等的前提下,对比 KAN 和 MLP 的性能差异。该实验涵盖多个领域,包括机器学习、计算机视觉、自然语言处理、音频处理以及符号公式表示。所有实验都采用了 Adam 优化器,这些实验全部在一块 RTX3090 GPU 上进行。
性能比较
机器学习。作者在 8 个机器学习数据集上进行了实验,使用了具有一到两个隐藏层的 KAN 和 MLP,根据各个数据集的特点,他们调整了神经网络的输入和输出维度。
对于 MLP,隐藏层宽度设置为 32、64、128、256、512 或 1024,并采用 GELU 或 ReLU 作为激活函数,同时在 MLP 中使用了归一化层。对于 KAN,隐藏层宽度则为 2、4、8 或 16,B 样条网格数为 3、5、10 或 20,B 样条的度数(degree)为 2、3 或 5。
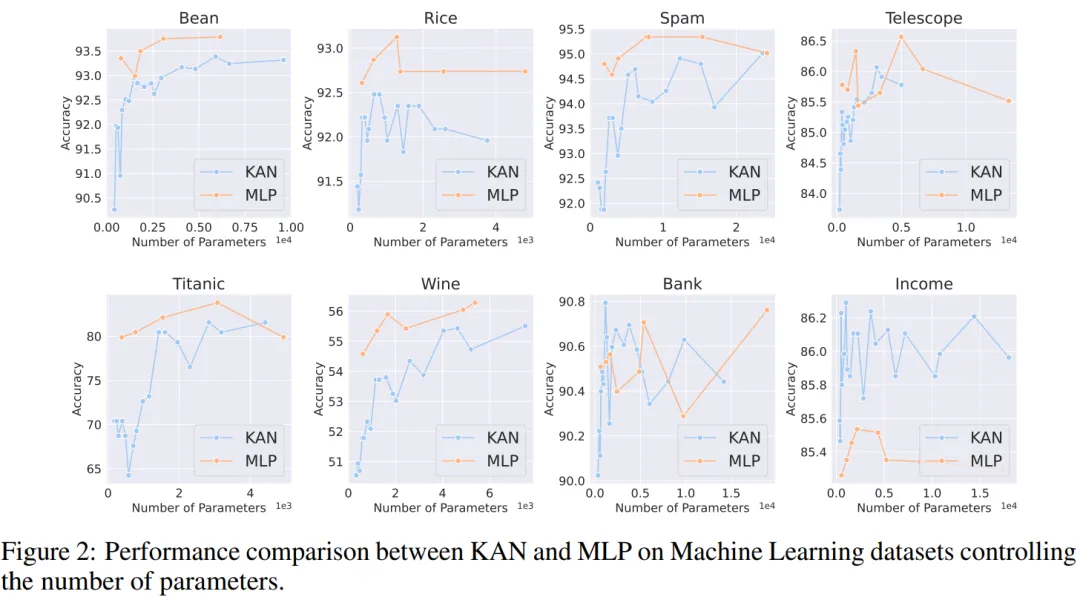
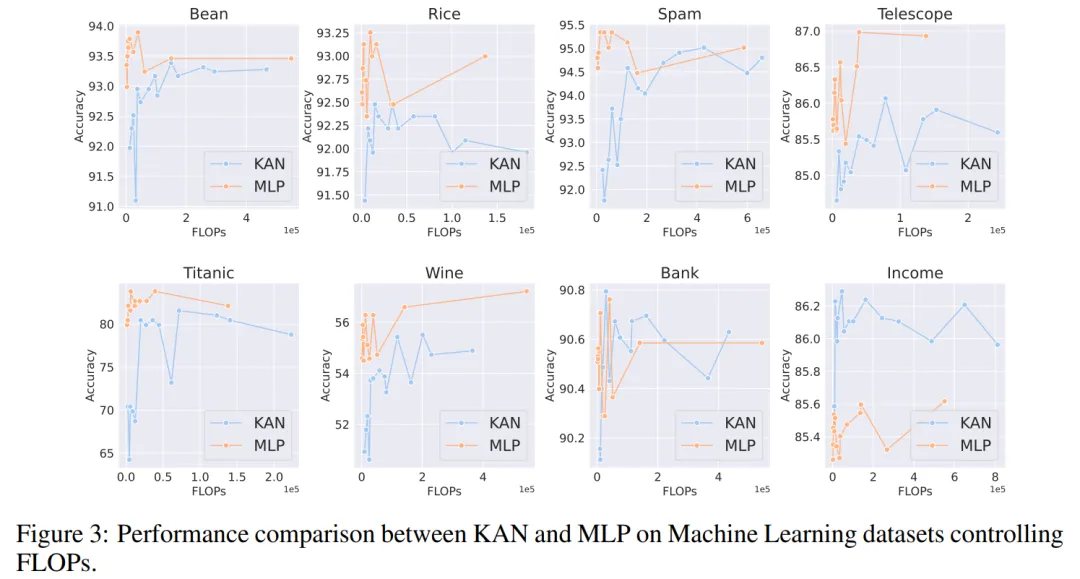
由于原始 KAN 架构不包括归一化层,为了平衡 MLP 中归一化层可能带来的优势,作者扩大了 KAN 样条函数的取值范围。所有实验都进行了 20 轮训练,实验记录了训练过程中在测试集上取得的最佳准确率,如图 2 和图 3 所示。
在机器学习数据集上,MLP 通常保持优势。在他们对八个数据集的实验中,MLP 在其中的六个上表现优于 KAN。然而,他们也观察到在一个数据集上,MLP 和 KAN 的性能几乎相当,而在另一个数据集上,KAN 表现则优于 MLP。
总体而言,MLP 在机器学习数据集上仍然具有普遍优势。
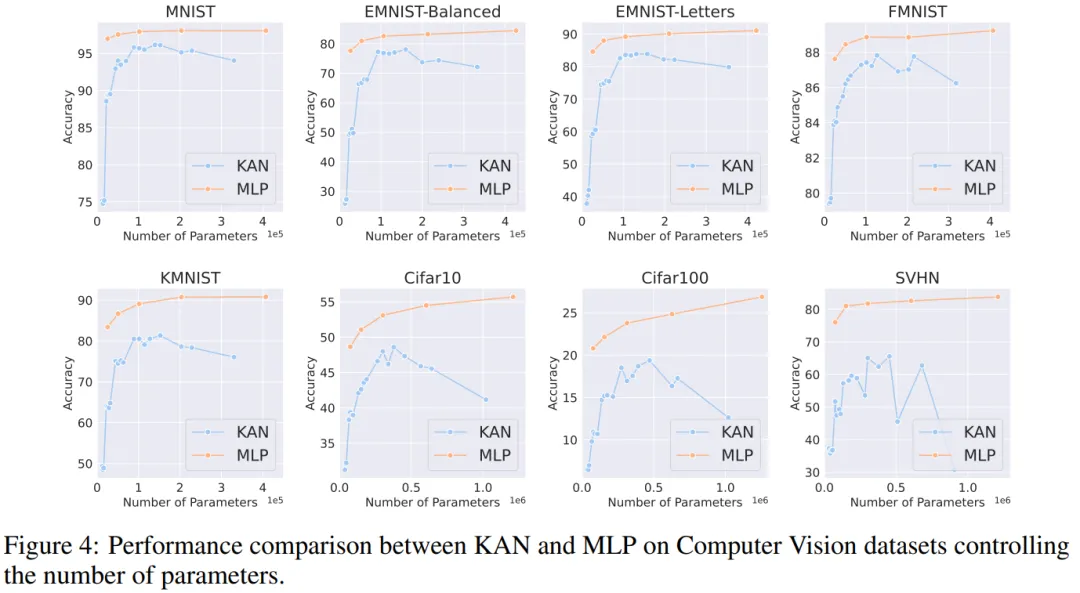
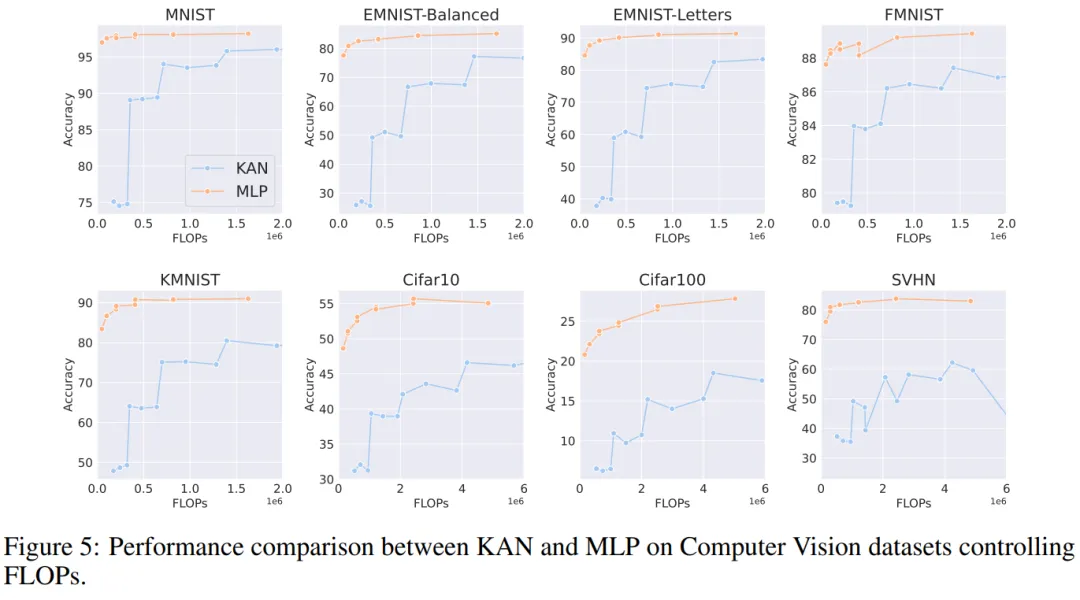
计算机视觉。作者对 8 个计算机视觉数据集进行了实验。他们使用了具有一到两个隐藏层的 KAN 和 MLP,根据数据集的不同,调整了神经网络的输入和输出维度。
在计算机视觉数据集中,KAN 的样条函数引入的处理偏差并没有起到效果,其性能始终不如具有相同参数数量或 FLOP 的 MLP。
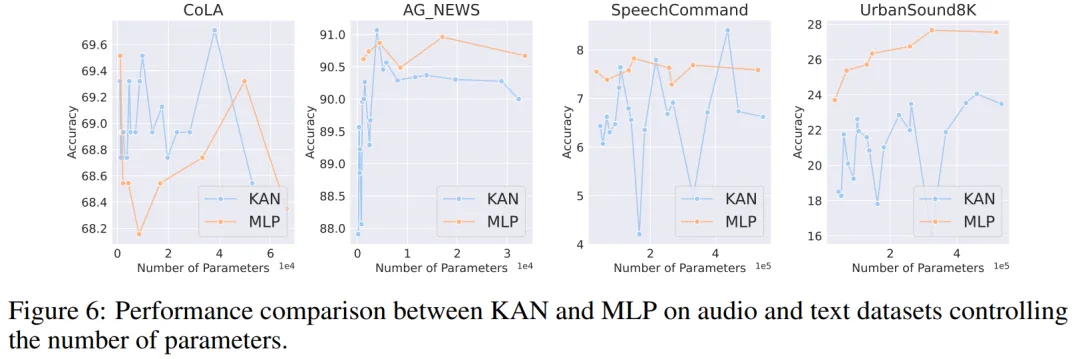
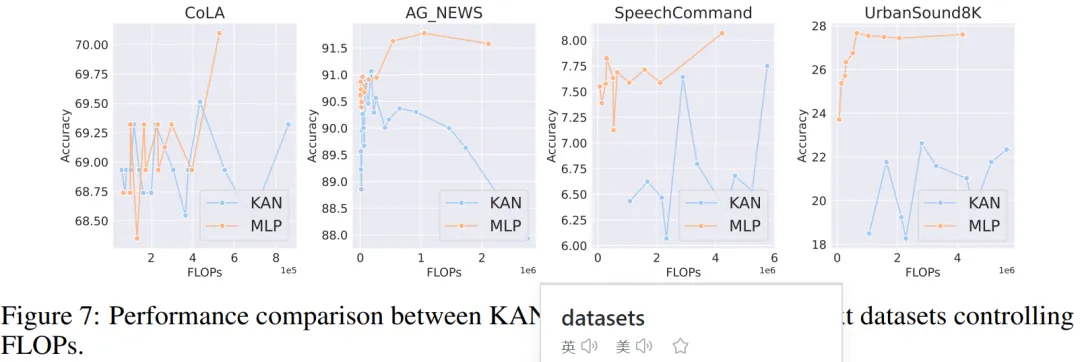
音频和自然语言处理。作者在 2 个音频分类和 2 个文本分类数据集上进行了实验。他们使用了一到两个隐藏层的 KAN 和 MLP,并根据数据集的特性,调整了神经网络的输入和输出维度。
在两个音频数据集上,MLP 的表现优于 KAN。
在文本分类任务中,MLP 在 AG 新闻数据集上保持了优势。然而,在 CoLA 数据集上,MLP 和 KAN 之间的性能没有显著差异。当控制参数数量相同时,KAN 在 CoLA 数据集上似乎有优势。然而,由于 KAN 的样条函数需要较高的 FLOP,这一优势在控制 FLOP 的实验中并未持续显现。当控制 FLOP 时,MLP 似乎更胜一筹。因此,在 CoLA 数据集上,并没有一个明确的答案来说明哪种模型更好。
总体而言,MLP 在音频和文本任务中仍然是更好的选择。
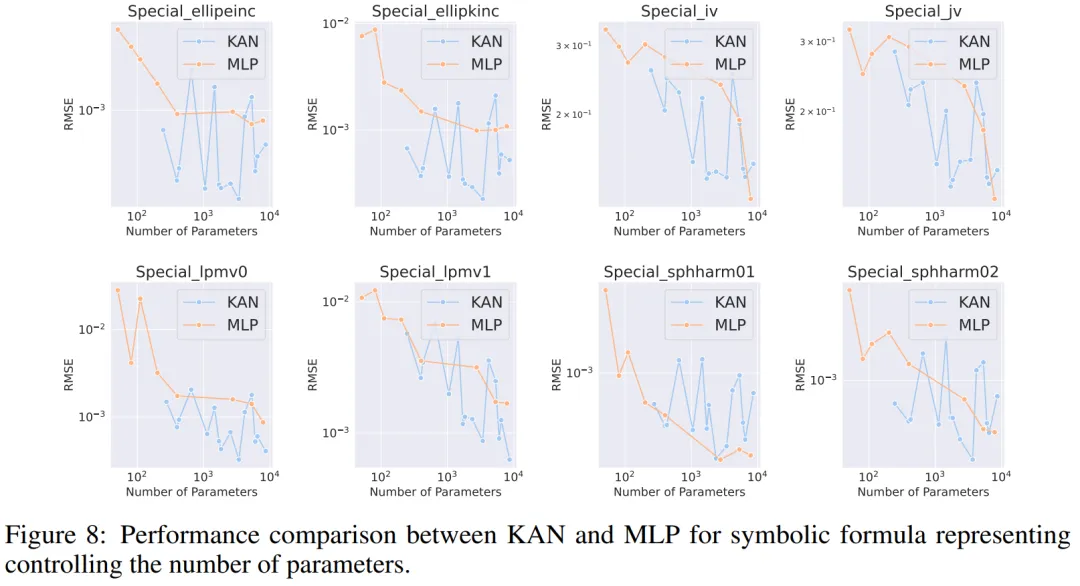
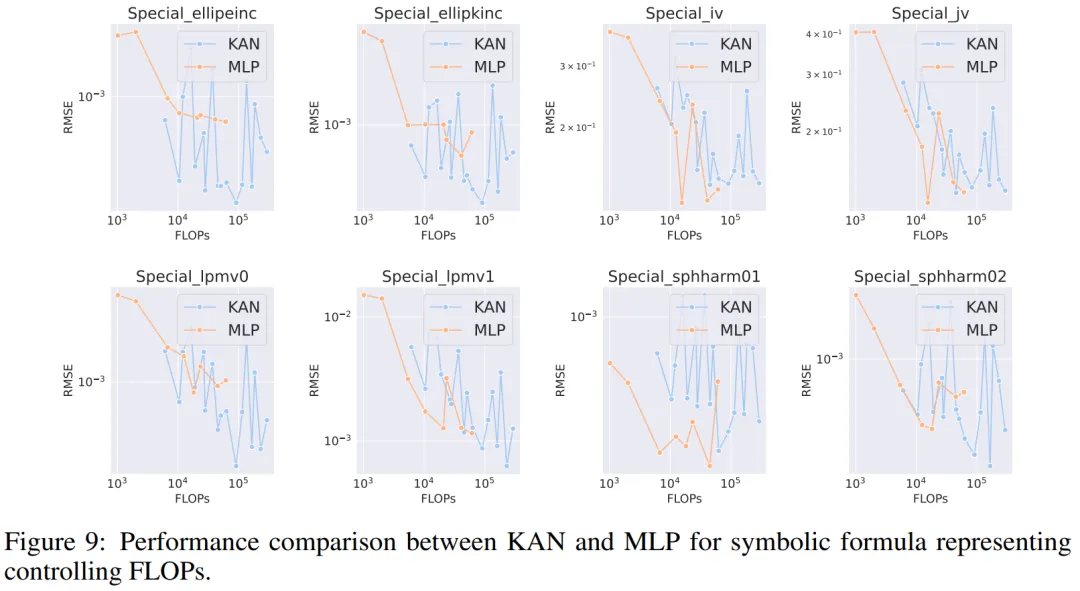
符号公式表示。作者在 8 个符号公式表示任务中比较了 KAN 和 MLP 的差异。他们使用了一到四个隐藏层的 KAN 和 MLP,根据数据集调整了神经网络的输入和输出维度。
在控制参数数量的情况下,KAN 在 8 个数据集中的 7 个上表现优于 MLP。在控制 FLOP 时,由于样条函数引入了额外的计算复杂性,KAN 的性能大致与 MLP 相当,在两个数据集上优于 MLP,在另一个数据集上表现不如 MLP。
总体而言,在符号公式表示任务中,KAN 的表现优于 MLP。