Transformer中的信息流动机制,被最新研究揭开了:
所有层都是必要的吗?中间层在做同样的事吗?层的顺序重要吗?
如果跳过一些层,比如第4层输出接到第6层会怎样。随机打乱层的顺序,比如4-6-5-7又会怎样。
最近一项名为“Transformer Layers as Painters”的研究火了,由来自AI初创公司Sakana AI、Emergence AI的研究团队完成。

他们从Transformer内部工作原理出发,经过一系列实验对以上问题得出了结论。团队表示深入理解这些原理不仅能提高现有模型利用效率,还能帮助改进架构开发新的变体。
谷歌DeepMind研究员、ViT作者Lucas Beyer看过后直接点了个赞:
很棒的总结!尽管一些实验在之前的研究中已经被展示过了,但我喜欢你添加的新细节,特别是强调了“推理”类任务比其他任务受影响更大!

还有不少学者、工程师也表示强烈推荐。
敢打赌,其中一些见解最终将会用于改进Transformer。

其中的实验再次证实了:复制层对创造性任务有帮助,但对推理任务通常无效;改变层的顺序行不通;剪枝在中间层效果最佳,但仍需要进行修复调整。

所以,在这项研究中,研究团队都进行了哪些实验?回答了哪些问题?
实验模型选择和基准
先来看一下实验配置~
实验在decoder-only和encoder-only模型上进行。
其中decoder-only模型选择的是Llama2,主要研究32层、70亿参数的Llama2-7B,扩展实验中也包含13B(40层)和70B(80层)模型。
encoder-only模型选择的是BERT,有24层、3.4亿参数。
研究人员使用这些模型的标准预训练checkpoints。在所有实验中,模型都是冻结的,除BERT的评估中包含一个标准的微调步骤,其它情况未通过微调等方法修改模型参数。
基准测试方面,Llama2使用以下标准基准:ARC(科学考试问题)、HellaSwag(常识问题)、GSM8K(数学题),WinoGrande(常识推理)、LAMBADA(词汇预测)。其中LAMBADA用于测困惑度,与训练期间使用的原始token预测最接近。
对于Llama2的性能评估,提供了基准测试的标准化中位数,将性能从0到1(模型最优性能)进行量化。
对于BERT,采用GLUE基准并遵循其评估指标,包括基准的未标准化平均分。注意,标准的BERT评估包括一个微调步骤,因此对模型进行了适应性调整。在附录中研究人员也展示了一个只有模型头部可以调整的评估结果。
实验动机最初源于这样一个问题:
是否可以将多个层以某种方式合并成一个可能更大的单一层?假设可能由于训练过程中使用了残差连接,神经网络的中间层可能使用了一个共同的表征空间。(对于标准的多层感知机来说不成立,它们之间没有促使共同表征或层间排列一致性的机制)
如果层能共享一个表征空间,将对后续条件计算或向预训练Transformer模型动态添加新知识及下游应用产生重要影响。
关于Transformer的8大问题
层是否使用相同的表征空间?
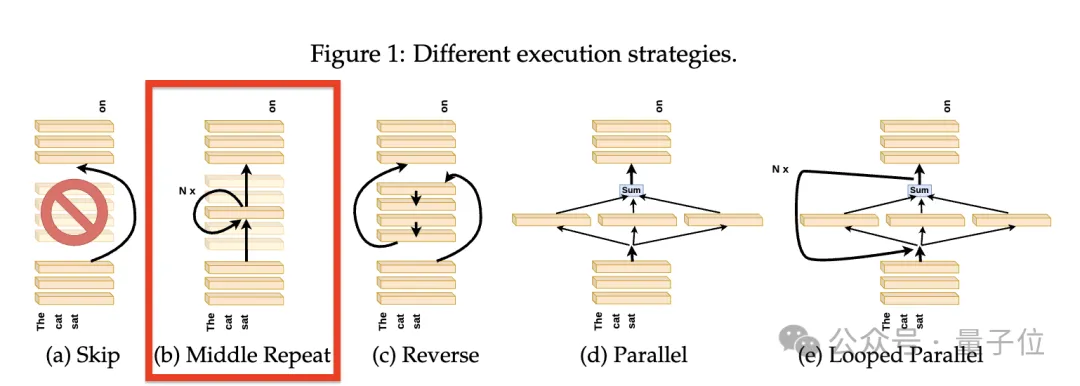
为确定不同层是否共享相同的表征空间,研究人员检验了Transformer对于跳过特定层或更改相邻层顺序的鲁棒性。
例如,在Llama2-7B模型中将输出流从“第4层->第5层->第6层”的正常顺序,改为“第4层->第6层”,跳过第5层,会怎样?
又或者将第4层的输出送到第6层,然后将第6层的输出送到第5层,再送到第7层,会怎样?
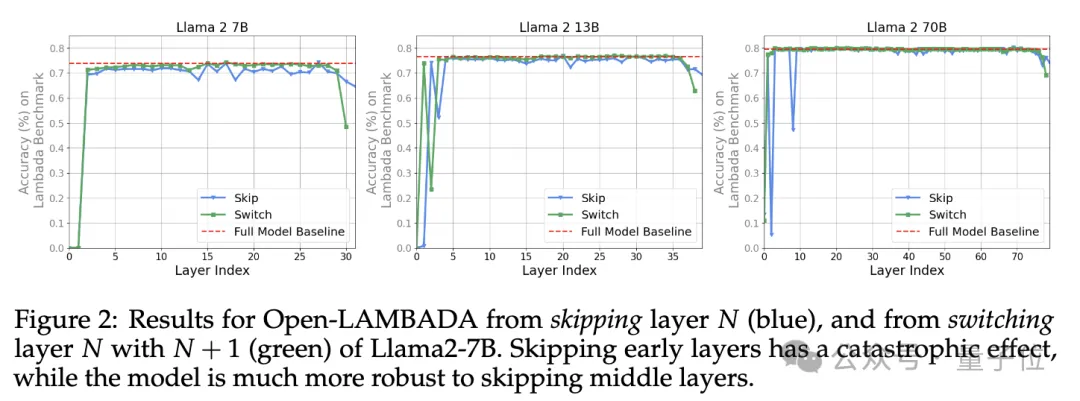
如下图所示,实验发现除了最前面的和最末尾的几层,Llama2-7B跳过或改变层序表现出很好的鲁棒性。
也就是说,中间层共享一个表征空间,中间层与“外层”(最前面的和最末尾的几层)具有独立的表征空间。
为了进一步证实这一假设,研究人员测量了不同模型(Llama2-7B、Llama2-13B和BERT-Large)中不同层的隐藏状态激活之间的平均余弦相似度,并跨基准测试进行了比较。
下图3展示了所有中间层之间的一致性。例如,底部第四层的激活与顶部第四层的激活高度相似。对于40层的Llama2-13B,可以看到这些层按相似性可划分成4-5个组:第0层,1-3层,中间层,然后是最后一两层。
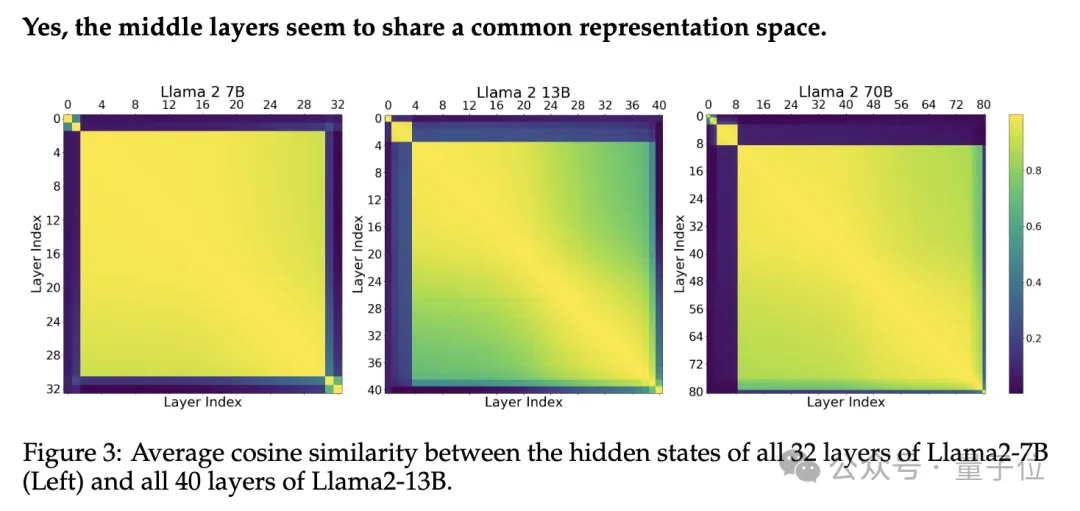
这表明模型可能对“开始”、“中间”和“结束”层具有三个不同的表征空间。研究人员还发现,“开始层”的数量似乎随着模型总层数的增加而增加。
此外,高余弦相似度可能证明有一个共享的表征空间,低相似度更能表明这些空间不是共享的。而上图3中Llama2-7B的数据与图2所示的性能结果高度一致,这进一步证明了:
至少中间层的表征空间是共享的。
所有层都是必要的吗?
为了进一步验证中间层的表征空间真正共享,研究人员还进行了层跳过实验(实验中未进行任何微调)。
具体来说,将第N层的输出直接传递为第N+M层的输入(M>1),从而“跳过”了M-1层,如下图所示。
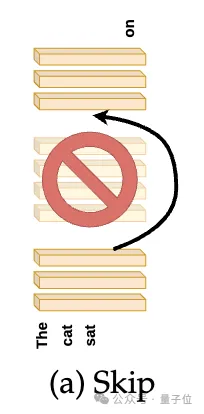
原本第N+M层仅针对来自第N+M-1层的输入进行训练,那么现在它能否理解第N层的激活?
此类实验中,研究人员正常执行第一层和最后N-1层,而跳过或修改第N+1到第T-N层(T是模型总层数)。
如下图4,在多个基准测试中,Llama2-7B和BERT-Large的性能均逐渐下降(图从左至右展示了跳过层数逐渐递增的变化)。这一结果揭示了:
不是所有层都是必要的,至少省略部分中间层不会对整体性能造成严重影响。

中间层是否都执行相同的功能?
如果中间层共享一个共同的表征空间,这些层是否多余?
为了解答该问题,研究人员重新进行了前面的“跳过”实验,但这次不是跳过中间层,而是用最中心层的权重替换了这些所有中间层的权重,如下图所示。
实际上就是在最中心层上循环执行了T-2N+1次,其中T是模型总层数(Llama2-7B为32层,BERT-Large为24层)。
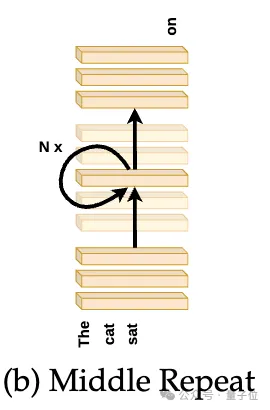
结果基准测试中,随着被替换的层数增加,模型性能迅速下降。而且性能下降速度比仅仅跳过某些层要严重得多,这种权重替换极具破坏性。
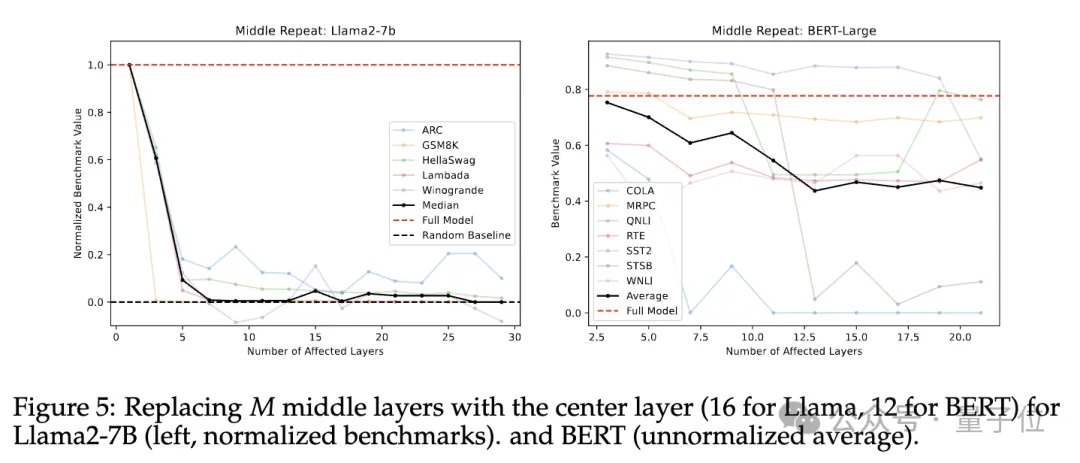
因此,中间层各执行不同的功能并非多余,中间层之间共享权重会产生灾难性后果。
层的顺序重要吗?
上面实验表明中间层虽共享表征空间,却在该空间上执行不同操作。那么这些操作顺序重要吗?研究人员进行了两组实验。
首先,将中间层按照与其训练顺序相反的顺序(逆序)执行。将第T-N层的输出传递给第T-N-1层,依此类推,直至第N层,然后将该层的输出传至最后的T-N层。
如下图:
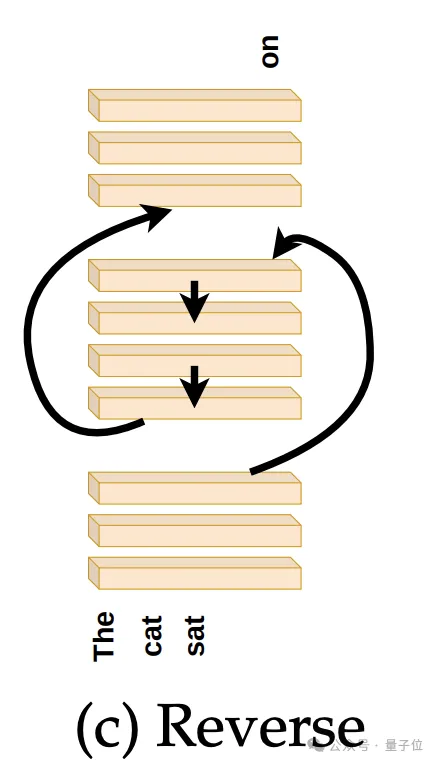
第二个实验,随机排列中间层顺序,并平均10个随机种子结果。
结果如下图,两种情况模型都呈现出缓慢的性能下降。
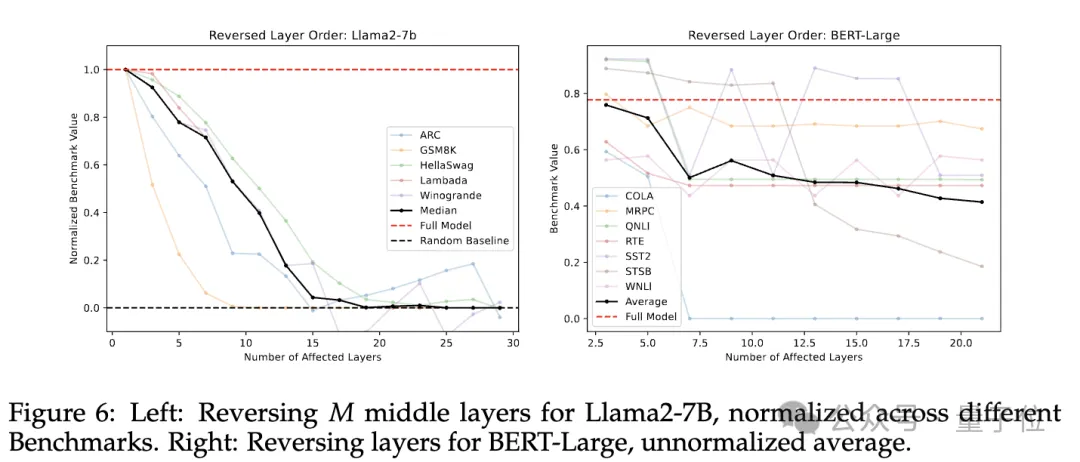
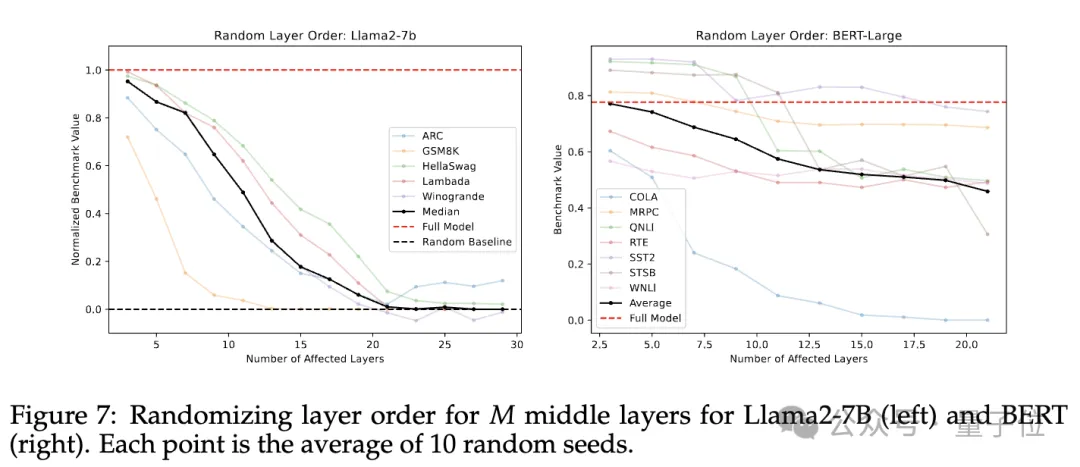
这里剧透一下下面的一项实验结果,无论是逆序还是随机顺序,模型表现均优于直接跳过这些层,说明即使层在非训练顺序的输入上运行,依然能进行有效输出。
因此,层顺序重要吗?结论是:
层顺序调整对性能有一定影响,随机顺序和逆序都表现出一定的性能退化。
值得注意的是,随机顺序性能优于逆序。可能是因为逆序与训练时的顺序完全相反,而任何随机顺序都至少保持了一些顺序上的连贯性(即某层i总在另一层j之后,其中i>j)。
可以并行运行这些层吗?
如果层的存在,即没有被跳过,比它们执行的顺序更重要,那么是否可以考虑独立地运行这些层,然后将它们的结果合并?如下图所示。
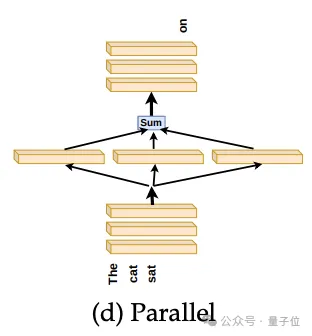
研究人员进行了一个实验,不是跳过第N到第T-N层,而是并行运行这些中间层,然后将它们的平均结果传递到最后的N层。
结果如下图所示,除了GSM8K数学题基准外,所有基准测试都表现出缓慢的性能退化。
有趣的是,并行层的表现优于跳过层,但不如逆序运行层。
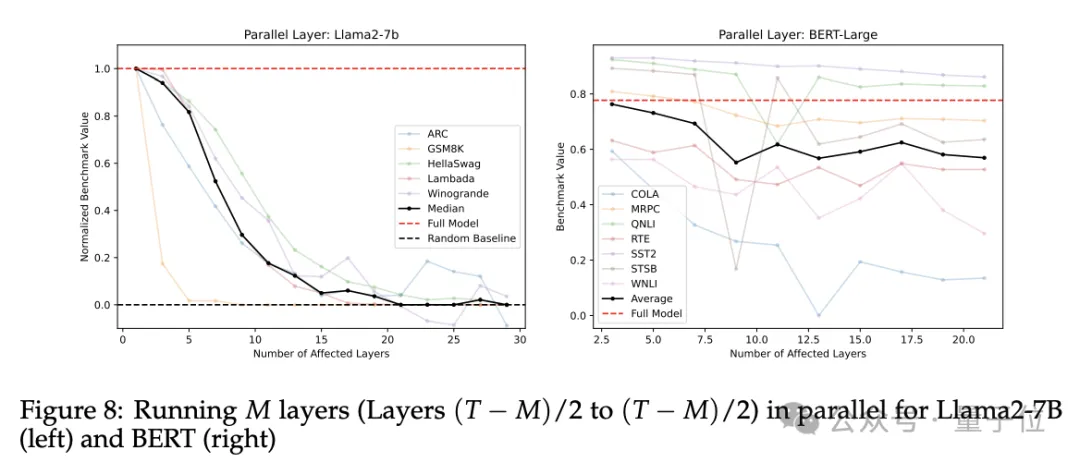
总之,可以并行运行这些层吗?答案是:可以,数学为主的基准测试除外。
对于某些任务,顺序是否更重要?
大多数变体(包括逆序、跳过和并行)在抽象推理ARC或数学推理GSM8K基准中,表现出最快速的性能下降。
可以解释为逐步推理任务比“语义”任务(如Winogrande或HellaSwag)对层顺序的变化更为敏感。
这是因为推理任务需要结合结构和语义双重信息,而HellaSwag这类任务仅需语义即可完成。
通过实验,研究人员得出结论:数学和推理任务比“语义”任务更依赖顺序。
迭代对并行层有帮助吗?
如果把Transformer内部运行机制比作是画一幅画的过程:画布(输入)在一些画家之间传递,一些画家专门画鸟,一些则更擅长画轮子……每个画家都依次从另一位画家手里接过画布,然后决定对这幅画进行补充,还是将其直接传递给下一位画家(使用残差连接)。
可以想象,某些层在收到适当的输入时才会对画作进行“补充”。例如,如果“画轮子”的画家先看到汽车的车身,才更有可能画上轮子。
在Transformer中,某些层可能只有在接收到适当的输入时才会对前向传递发挥作用,而不是通过残差连接将输入直接传递出去。
这么来看的话,那么相比于仅执行一次并行层,迭代执行并行层应该会提高性能。
研究人员通过将并行层的平均输出回馈到同一层并固定迭代次数来进行测试,如下图:
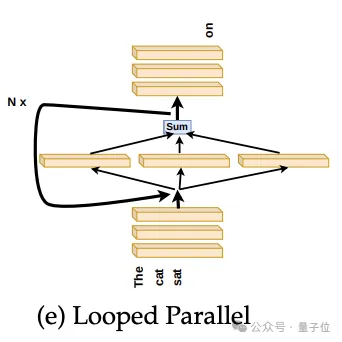
下图9中,研究人员展示了并行层迭代3次的结果,这种方法显著优于仅执行一次并行层。
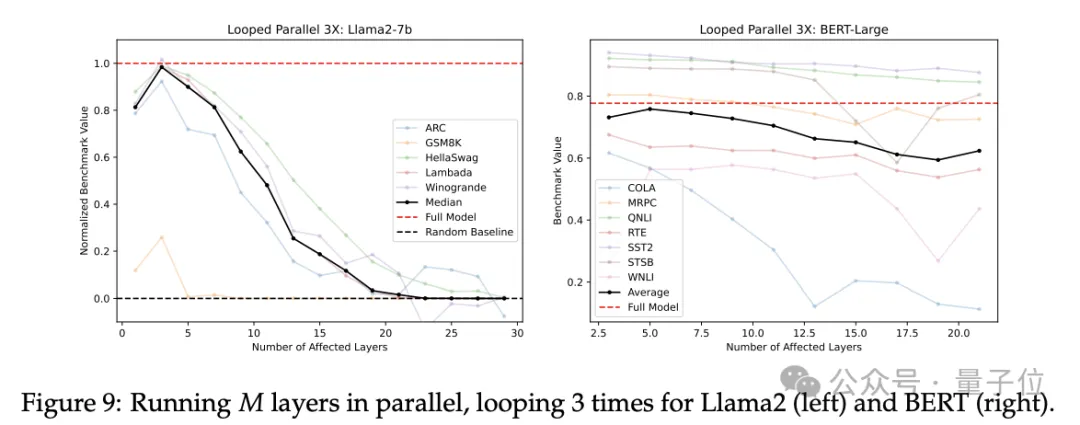
唯一的例外是在Llama2-7B的起始层N为15或BERT的起始层N为11时。在这种情况下,循环并行3次的效果相当于仅重复中间层3次,此时的并行层等同于完整模型。
研究人员还用不同的迭代次数重复进行了实验。
下图展示了Llama2-7B的性能随并行层数M和迭代次数的变化而变化。
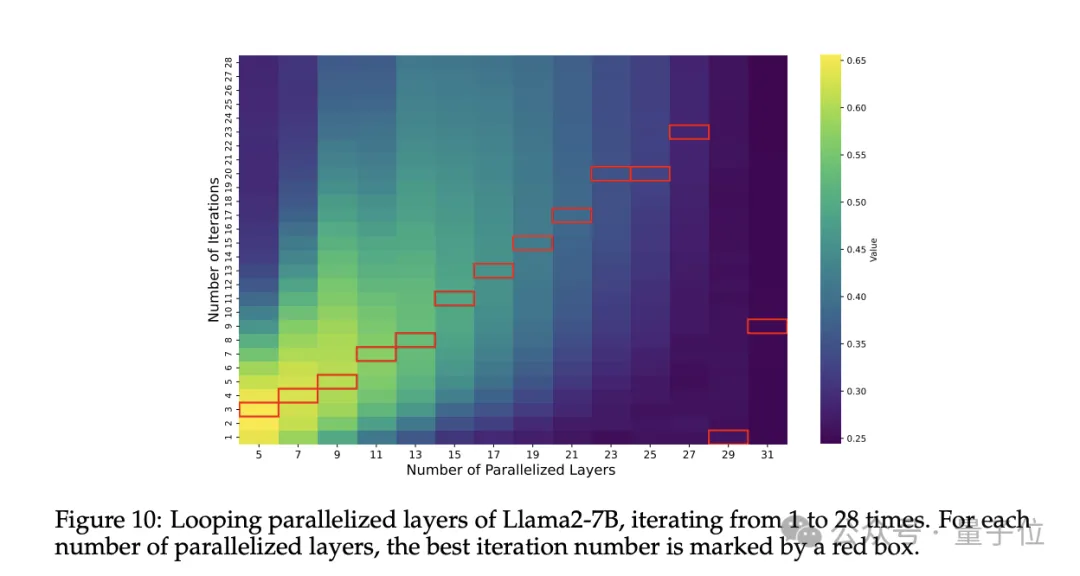
每个M的最佳迭代次数用红框表示。除了M=29和M=31(几乎并行所有层)外,最佳迭代次数大致与并行层数成线性比例。
因此结论是:迭代对并行层有帮助,最佳迭代次数与并行层数成比例。
哪些变体对性能损害最小?
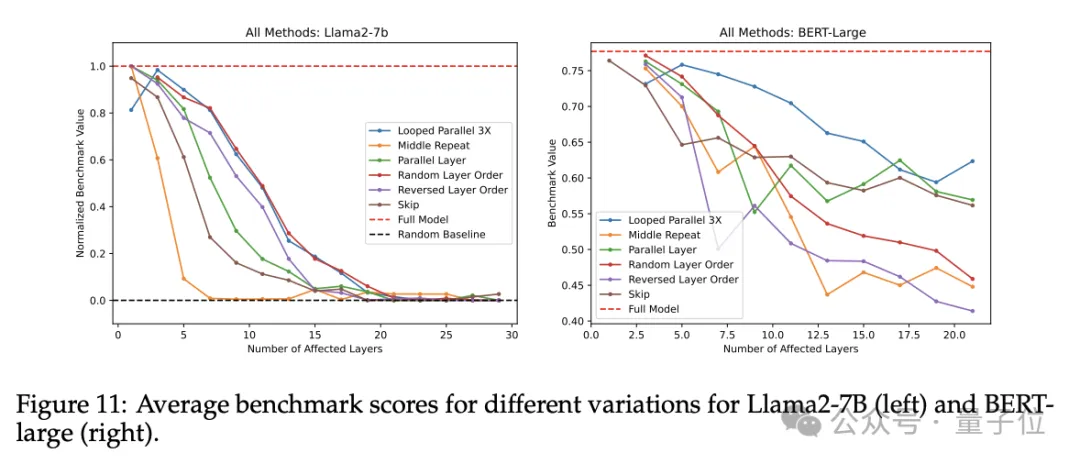
最后,研究人员将实验中的所有不同变体在同一图表上进行了比较。
结果显示,重复单一层(如上面提到的用同等数量的最中心的层替换中间层)效果最差,性能迅速退化至随机基准线。
迭代并行和随机层顺序性能退化最小,其中迭代并行在BERT和Llama2-7B中表现最好。
论文附录中还补充了更多实验结果,感兴趣的家人们可以查看原论文。
论文链接:https://arxiv.org/abs/2407.09298v1
参考链接:https://x.com/A_K_Nain/status/1812684597248831912































