大家好,我是小寒。
今天给大家分享神经网络中的一个重要知识点,激活函数
在神经网络中,激活函数(Activation Function)是神经元计算的一部分,决定了一个神经元在接收到输入信号后的输出。
激活函数通过引入非线性特性,使神经网络能够学习复杂的模式和表示。
什么是激活函数
激活函数使神经网络能够学习和模拟输入数据和目标变量之间复杂的非线性关系。
通过引入非线性特性,激活函数可以帮助网络处理涉及复杂函数映射的任务,而这些任务仅靠线性函数无法解决。
 图片
图片
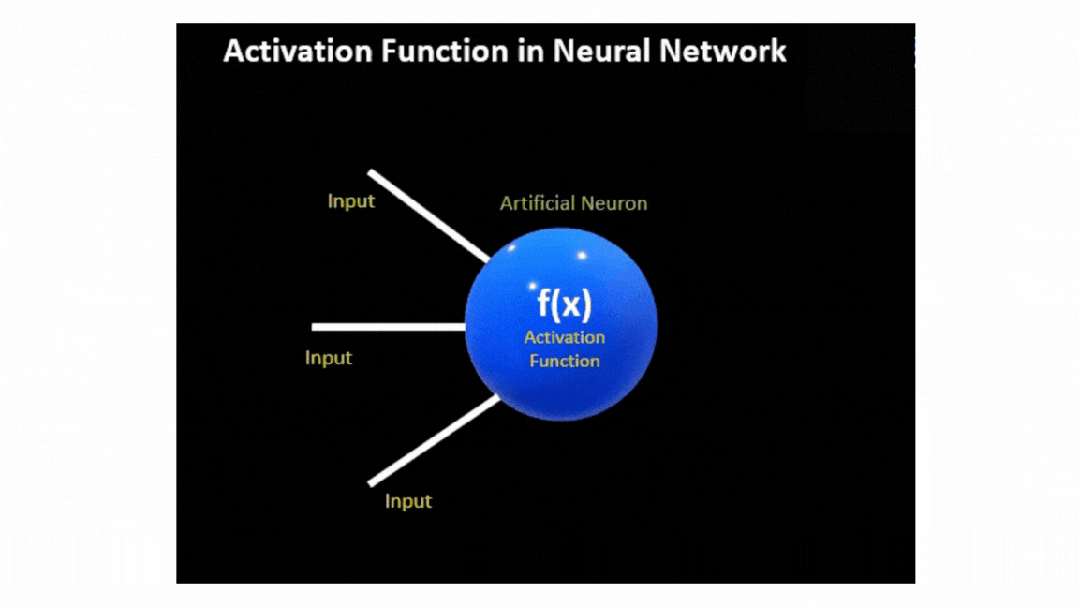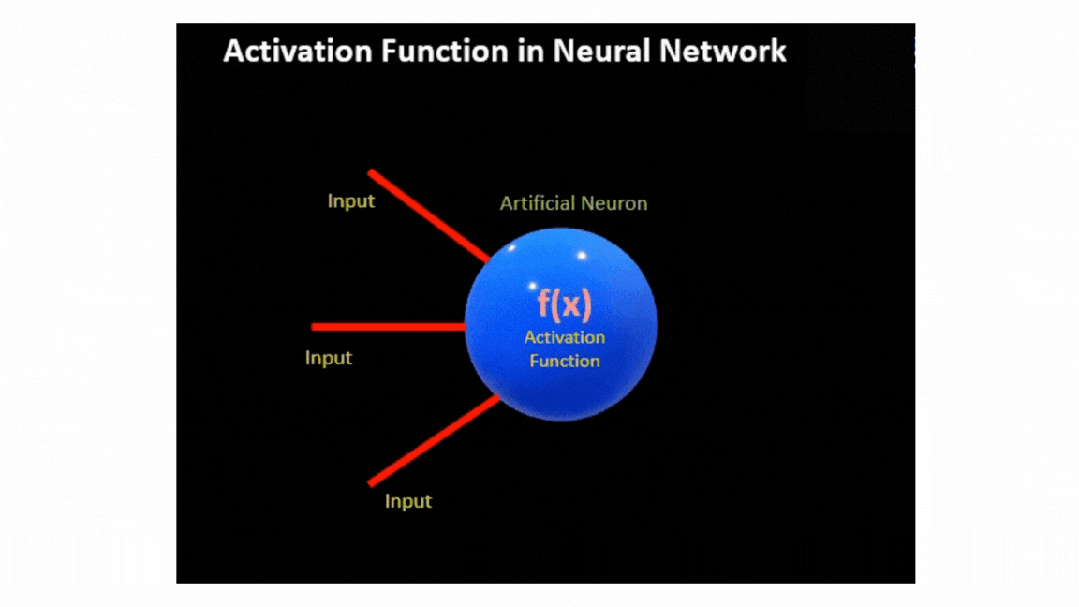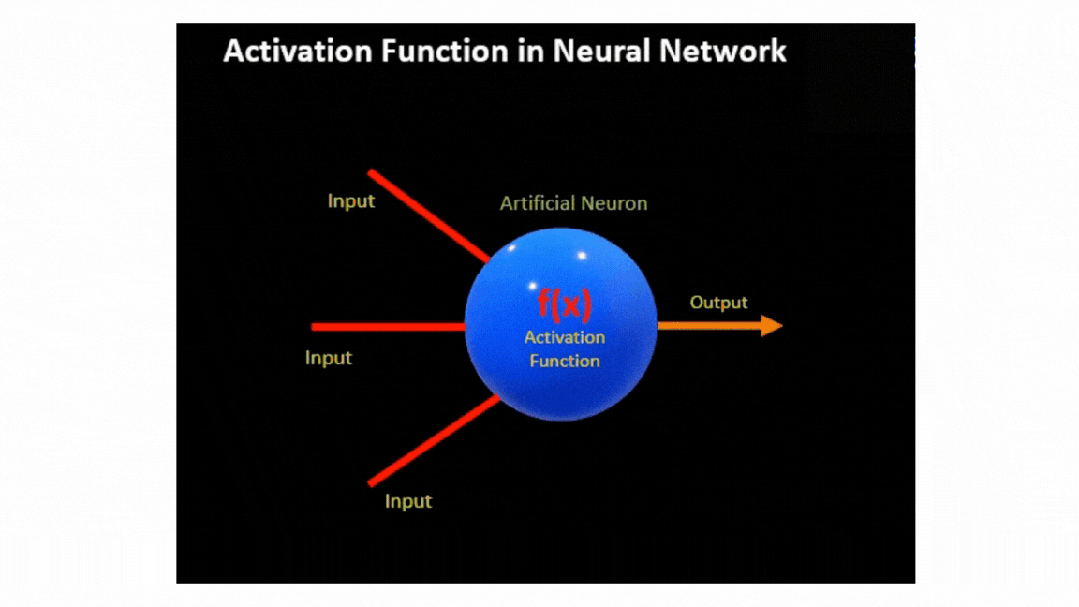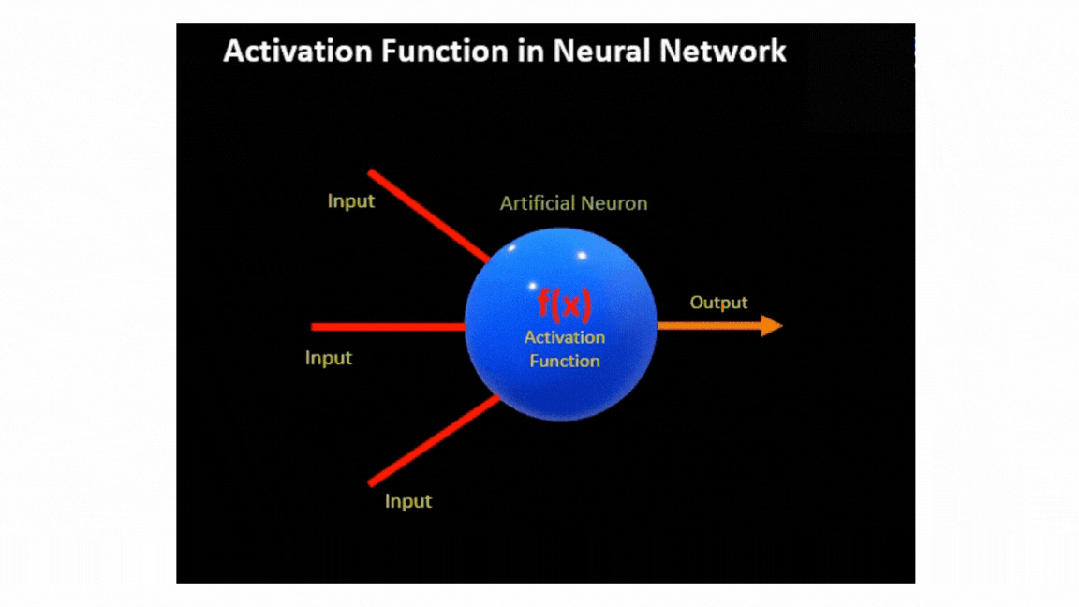
实际上,在神经网络中,神经元的输出是通过对输入特征 X 及其相应权重 W 的乘积加上偏差 b
然后,将该线性组合传递到激活函数 f(x),从而引入必要的非线性和输出信号。
现在,这些信号成为后续层的输入,使网络能够构建数据的分层表示。
该机制确保 ANN 能够从多样化和非线性的数据分布中进行概括和学习。
常见的激活函数
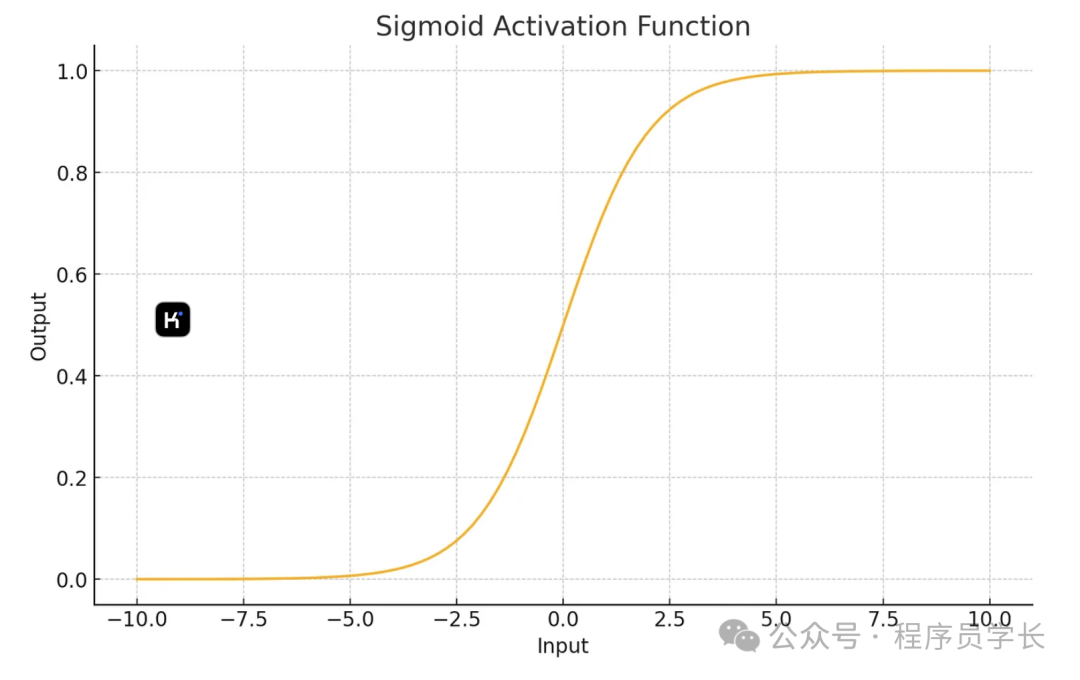
1.Sigmoid 激活函数
Sigmoid 函数的公式为:
 图片
图片
特点:
- 输出范围在 (0, 1) 之间。
- 常用于二分类问题的输出层。
- 有平滑、单调递增的特性。
- 存在梯度消失问题,尤其在深层网络中会导致训练缓慢。
Python实现
import numpy as np
import matplotlib.pyplot as plt
def sigmoid(x):
return 1 / (1 + np.exp(-x))
x = np.linspace(-10, 10, 100)
y = sigmoid(x)
plt.plot(x, y)
plt.title("Sigmoid Activation Function")
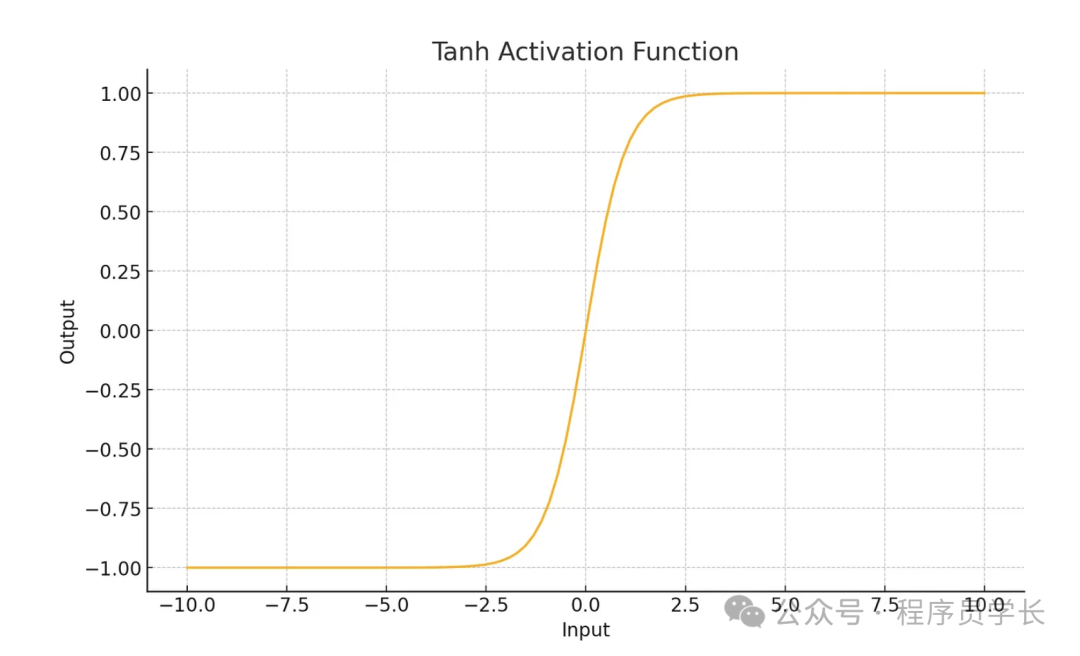
plt.show()2.Tanh
Tanh(双曲正切)函数的公式为:
 图片
图片
特点:
- 输出范围在 (-1, 1) 之间。
- 比 Sigmoid 更适合深层网络,因为其输出均值为 0,使得数据更容易居中。
- 同样存在梯度消失问题,但比 Sigmoid 稍微好一些。
Python 实现
def tanh(x):
return np.tanh(x)
y = tanh(x)
plt.plot(x, y)
plt.title("Tanh Activation Function")
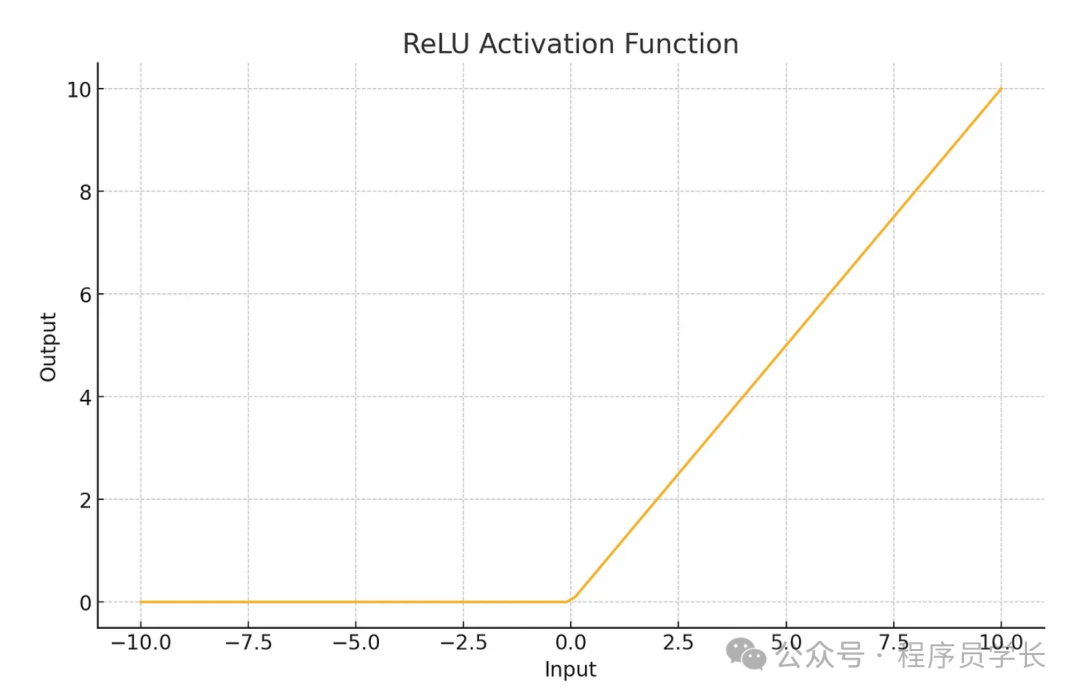
plt.show()3.ReLU
ReLU(Rectified Linear Unit)函数的公式为:
 图片
图片
特点:
- 输出范围在 [0, ∞) 之间。
- 计算简单,收敛速度快,广泛应用于各种神经网络中。
- 存在 “死亡 ReLU” 问题,当输入值为负时,梯度为 0,可能导致神经元不会再被更新。
Python 实现
def relu(x):
return np.maximum(0, x)
y = relu(x)
plt.plot(x, y)
plt.title("ReLU Activation Function")
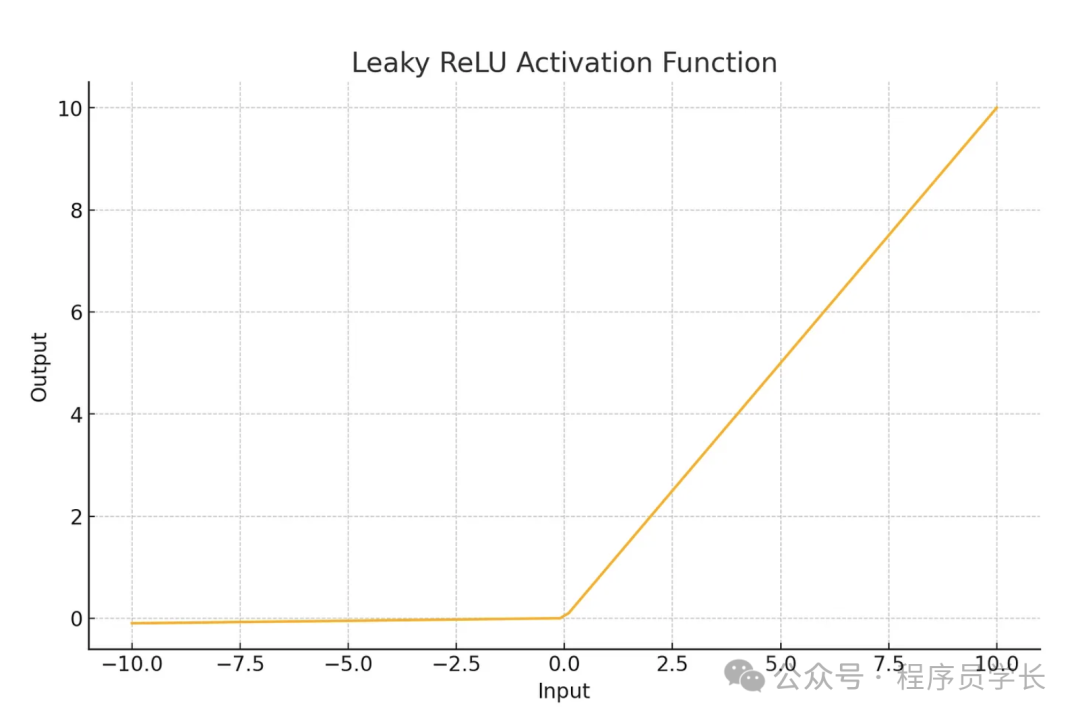
plt.show()4.Leaky ReLU
Leaky ReLU 是 ReLU 的变种,允许负值通过一个很小的斜率,公式为
 图片
图片
特点
- 解决了 ReLU 函数中神经元“死亡”的问题。
- 允许少量的负值梯度流过,从而保持神经元的更新。
python 实现
def leaky_relu(x, alpha=0.01):
return np.where(x > 0, x, alpha * x)
y = leaky_relu(x)
plt.plot(x, y)
plt.title("Leaky ReLU Activation Function")
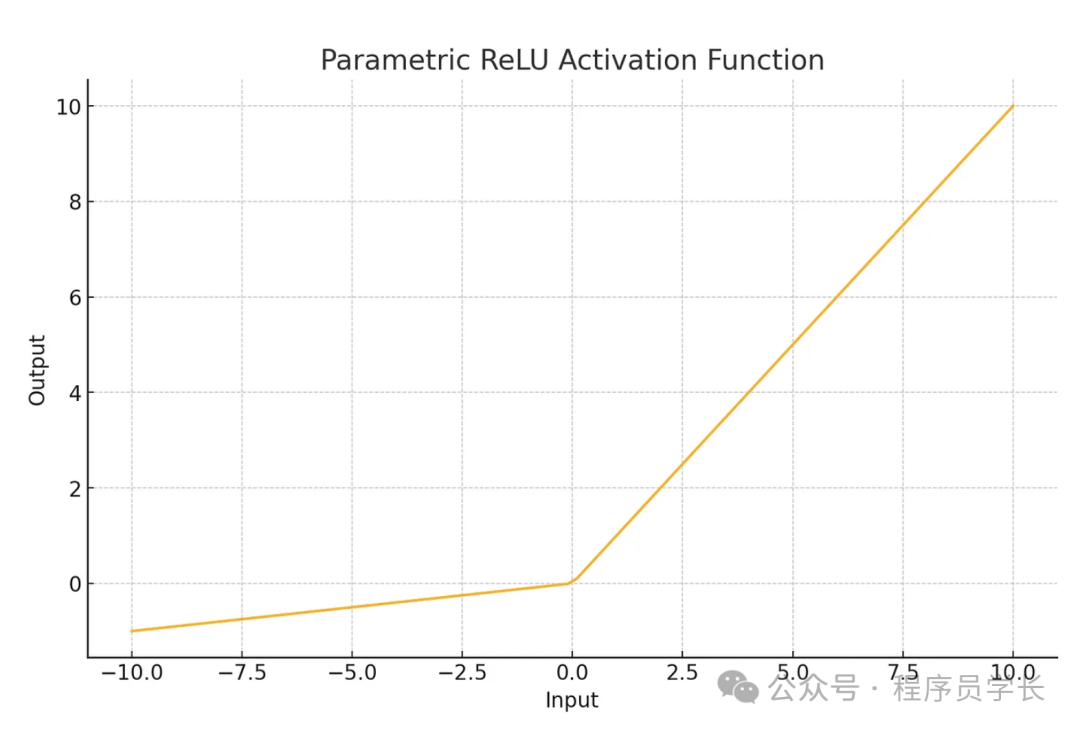
plt.show()5.PReLU
其公式为
 图片
图片
特点
- 是 Leaky ReLU 的推广,其中 是一个可训练的参数。
- 更灵活,能适应不同的数据分布。
Python实现
def prelu(x, alpha):
return np.where(x > 0, x, alpha * x)
alpha = 0.1 # This would be learned during training
y = prelu(x, alpha)
plt.plot(x, y)
plt.title("Parametric ReLU Activation Function")
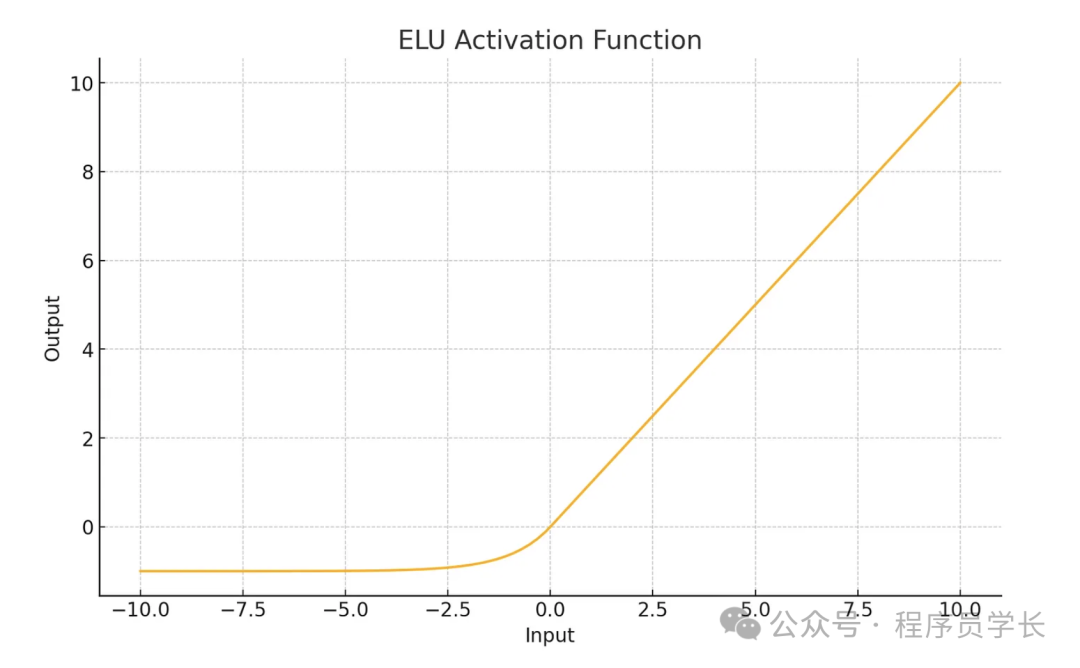
plt.show()6.ELU
其公式为
 图片
图片
特点
- 当 x > 0 时,ELU 的行为与 ReLU 类似,输出为 x 本身。
- 当 x ≤ 0 时,ELU 输出一个负值,形如 ,其中 是一个超参数。
- 负值部分的平滑特性可以使得平均激活接近 0,从而加快收敛速度。
- 相较于 ReLU,ELU 在负值部分具有更好的特性,可以减轻梯度消失问题,同时保留了 ReLU 的大部分优点。
Python 实现
def elu(x, alpha=1.0):
return np.where(x > 0, x, alpha * (np.exp(x) - 1))
y = elu(x)
plt.plot(x, y)
plt.title("ELU Activation Function")
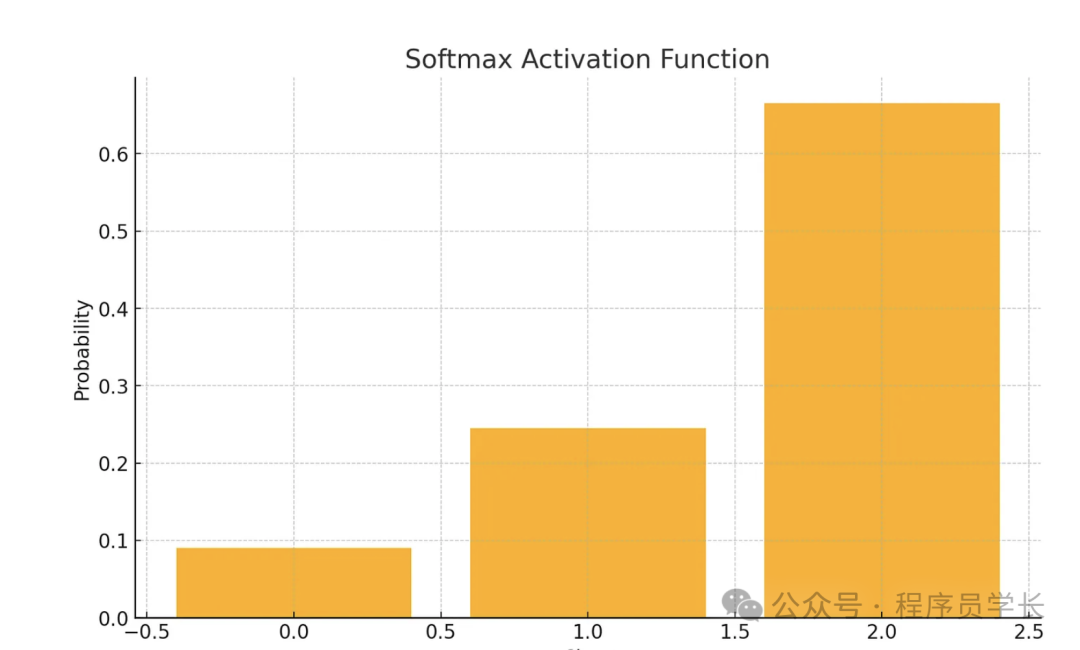
plt.show()7.Softmax 函数
公式为
 图片
图片
特点
- 常用于多分类问题的输出层。
- 输出的是一个概率分布,所有输出值的和为1。
python 实现
def softmax(x):
exp_x = np.exp(x-np.max(x))
return exp_x / exp_x.sum(axis=0)
y = softmax(x)
plt.plot(x, y)
plt.title("Softmax Activation Function")
plt.show()










































