斯坦福博士图解AlphaFold 3：超多细节+可视化还原ML工程师眼中的AF3

谷歌DeepMind的人工智能模型AlphaFold 3两个月前横空出世，颠覆了生物学。

这个「值得获得诺贝尔奖的发明」不仅在学术圈引起了巨震，还轰动了制药界——它可能带来数千亿美元的商业价值，并对药物研发产生深远影响。

论文地址：https://www.nature.com/articles/s41586-024-07487-w

如此重要的AlphaFold3，其具体工作原理是什么？

因为AlphaFold3的结构非常复杂，论文有相当高的阅读门槛，让人望而却步。两位斯坦福大学的两位博士生制作了一个论文的「图解版」，比论文阅读起来友好多了，而且还很详尽！

每一位机器学习工程师都不应该错过这篇图文并茂的文章——

博客地址：https://elanapearl.github.io/blog/2024/the-illustrated-alphafold/

此前已经有很多关于蛋白质结构预测的研究动机、CASP竞赛、模型失效模式、关于评估的争论、对生物技术的影响等主题的文章，因此以上内容都不是这篇博文关注的重点。

这篇博文关注的重点在于AlphaFold3（以下简称AF3）是如何在技术上实现的：分子在模型中被如何表示，它们又是如何被转换成预测结构的？

架构概述

AlphaFold3和前代模型最大的不同点在于——预测目标不同。

AF3不仅预测单个蛋白质序列（AF2）或蛋白质复合物（AF-multimeter）的结构，还能预测蛋白质与其他蛋白质、核酸、小分子中的一种或多种物质的复合结构，而且仅根据序列信息。

因此，前代的AF模型只需表示标准的氨基酸序列，但AF3需要引入更复杂的输入类型，因此设计了更复杂的特征表示和tokenization机制。

tokenization过程会在稍后单独描述，目前我们只需要知道，token可能代表单个氨基酸（蛋白质）、核苷酸（DNA/RNA），或者单个原子（其他物质）。

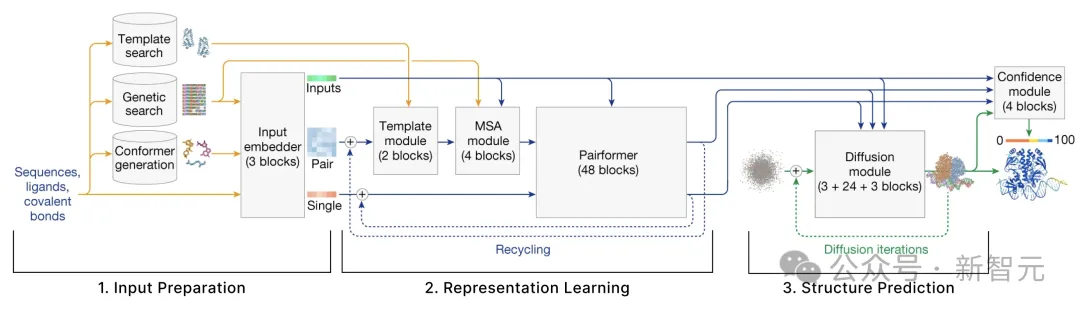
模型主要由3部分组成：

- 输入准备：给定输入的分子序列，模型需要检索一系列的结构相似的分子。这一步骤会识别出这些分子，并将其编码为数值张量。

- 表征学习：给定上一步中创建的张量，使用注意力机制的多种变体来更新这些表征。

- 结构预测：基于第一部分创建的原始输入以及第二部分改进后的表征，使用条件扩散进行结构预测。

在整个模型中，蛋白质复合物有两种表示形式：单一表征（single representation）和配对表征（pair representation），这两种表示都可以应用于token级别或原子级别。

前者仅仅表示复合物中的所有token或原子，后者则表征了物质中所有token/原子之间的关系（如距离、潜在相互作用等）。

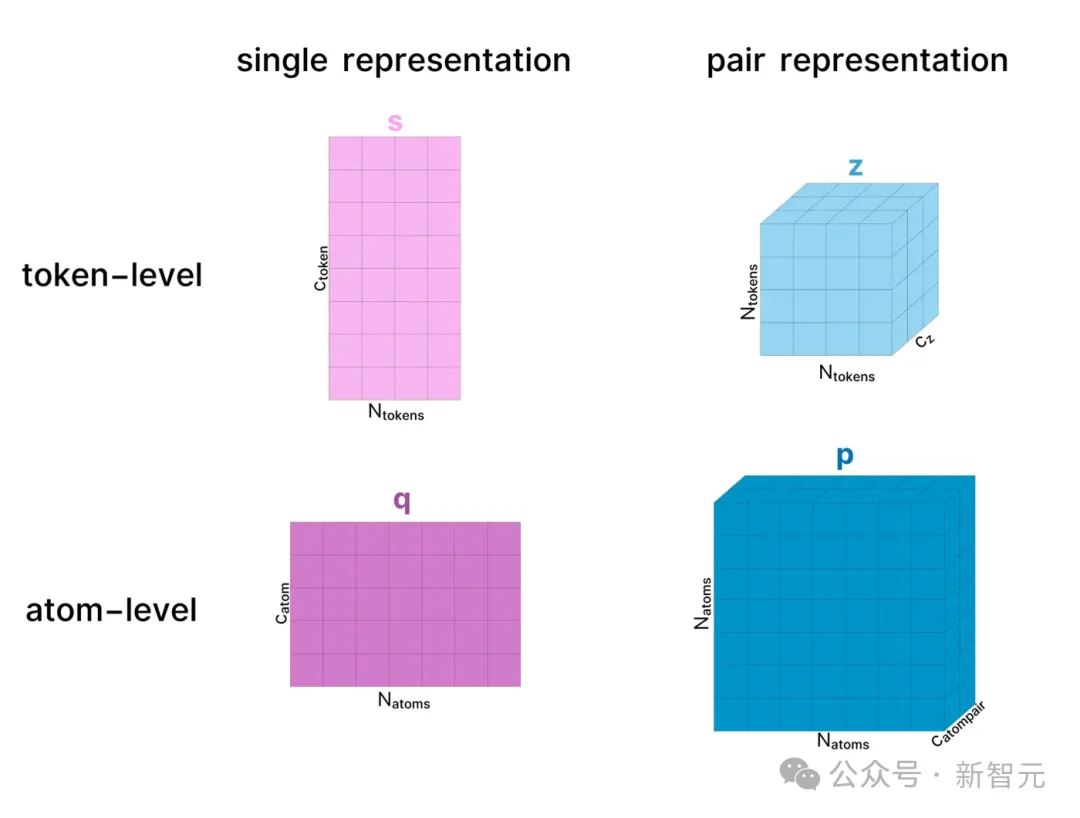
为了简单起见，下述的结构中忽略了大多数LayerNorm层，但其实它们无处不在。

输入准备

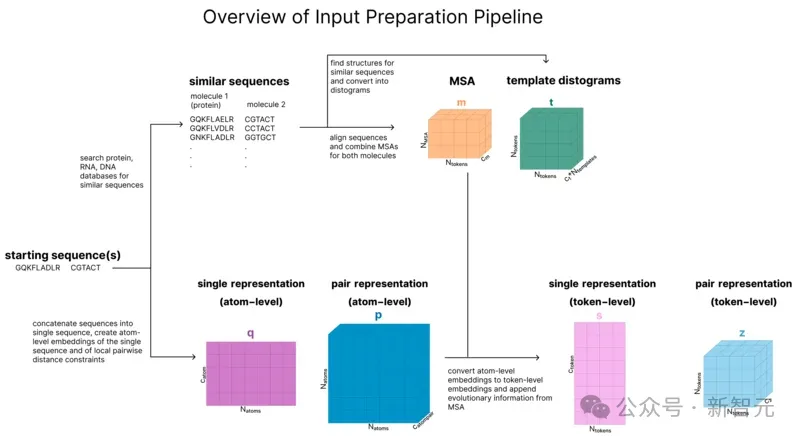
用户向AF3提供的实际输入是一个蛋白质序列和可选的其他分子。

本节的目标是将这些序列转换成一系列6个张量，这些张量将作为模型主干的输入.

如图所示，这6个张量分别是：

-s（token级单一表征）

-z（token级配对表征）

-q（原子级单一表征）

-p（原子级配对表征）

-m（MSA表征）

-t（模板表征）

本节包含5个步骤，分别是tokenization、检索、创建原子级表征、更新原子级表征、原子级到token级集成。

tokenization

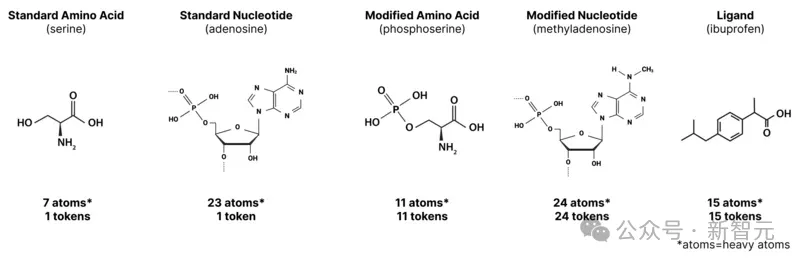
在AF2中，由于模型只表示具有固定氨基酸集的蛋白质，因此每个氨基酸都拥有自己的token。

AF3保留了这一点，但也引入了额外的token，以便处理其他分子类型：

-标准氨基酸：1个token（同AF2）

-标准核苷酸：1个token

-非标准氨基酸或核苷酸（甲基化核苷酸、翻译后修饰的氨基酸等）：每个原子1个token

-其他分子：每个原子1个token

因此，我们可以认为某些token（如标准氨基酸/核苷酸）对应多个原子，而其他token （如配体中的原子）只对应单个原子。

比如，35个标准氨基酸的序列（可能大于600个原子）将由35个token来表示；同时，一个由35个原子组成的配体也同样由35个token表示。

检索

AF3的早期关键步骤之一类似于语言模型中的检索增强生成（Retrieval Augmented Generation，RAG）。

模型会检索到与与输入序列相似的序列（收集到多序列比对中，即MSA），以及与这些序列相关的任何结构（称为「模板」），将它们作为模型的附加输入，分别写作m和t。

与AF-multimer相比，这些检索步骤中唯一的新内容是，除了蛋白质序列外，我们现在还对RNA序列进行检索。

请注意，这在传统上并不被称为「检索」，因为早在RAG这个术语出现之前，使用结构模板指导蛋白质结构建模就已经是同源建模领域的常见做法了。

不过，尽管AlphaFold没有明确将这一过程称为检索，但它确实与现在流行的RAG非常相似。

那么，模板（templates，t）如何表征呢？

通过模板搜索，我们获得了每个模板的三维结构，以及有关哪些token位于哪些链中的信息。

首先，计算给定模板中所有token对之间的欧氏距离。如果是对应多个原子token，则使用一个有代表性的「中心原子」来计算距离。

比如，对于氨基酸来说，中心原子是C_ɑ原子，而标准核苷酸的中心原子是C1'原子。

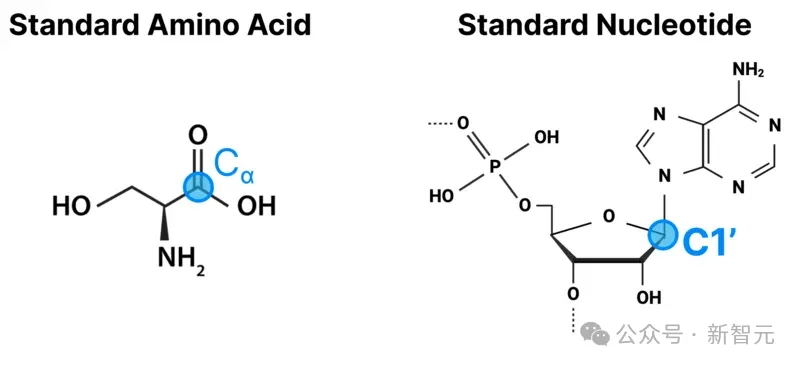
这会为每个模板生成一个N_token x N_token大小的矩阵。不过，距离并不是用数值来表示，而是将距离离散化为「距离直方图」。

然后，我们向每个直方图添加元数据，关于每个token属于哪个链、该token是否在晶体结构中得到解析、以及每个氨基酸内部的局部距离信息。

然后，我们对这个矩阵进行掩码，只查看每条链内部的距离（忽略链之间的距离）。根据论文的解释，这样做的原因是「并不尝试选择模板......以获取链间交互的信息」。

创建原子级表征

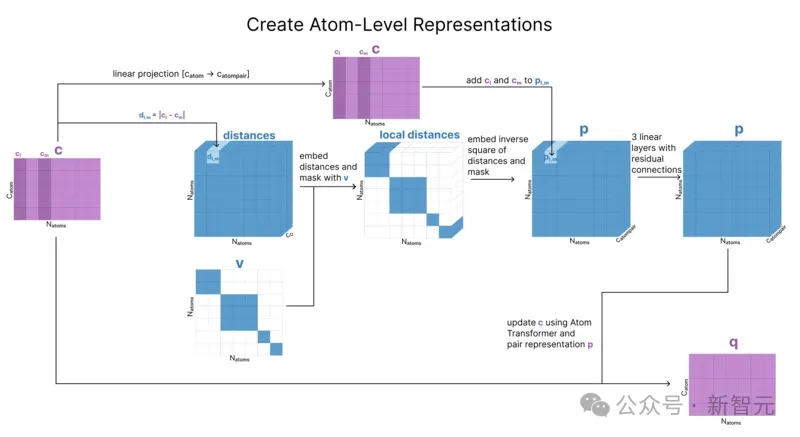
为了创建q（原子级单一表征），我们需要提取所有原子级特征。

第一步是计算每个氨基酸、核苷酸和配体的「参考构象」（reference conformer）。虽然我们还不知道整个复合物的结构，但我们对每个单独组件的局部结构有很多的先验知识。

构象（构象异构体的简称）是分子中原子的三维排列，通过对单键的旋转角度进行采样而生成。

每种氨基酸都有一个「标准」构象，但这只是该氨基酸存在的低能量构象之一，可以通过查表找到。

不过，每个小分子都需要生成自己的构象，利用RDKit中的ETKDGv3算法，同时结合了实验数据和扭转角偏好来生成三维构象。

然后，我们将该构象信息（相对位置）与每个原子的电荷、原子序数和其他标识符连接起来。矩阵c存储了序列中所有原子的这些信息。

然后，我们用c来初始化原子级别的配对表征p，以存储原子间的相对距离。

由于我们只知道每个token内的参考距离，因此先使用掩码机制（v）来确保这个初始距离矩阵只代表我们在构象生成过程中计算出的距离。

最后，我们将原子级别的单一表征复制一份，并将这个副本称为q。这个矩阵q是我们接下来要更新的，但c确实会被保存并稍后使用。

原子Transformer

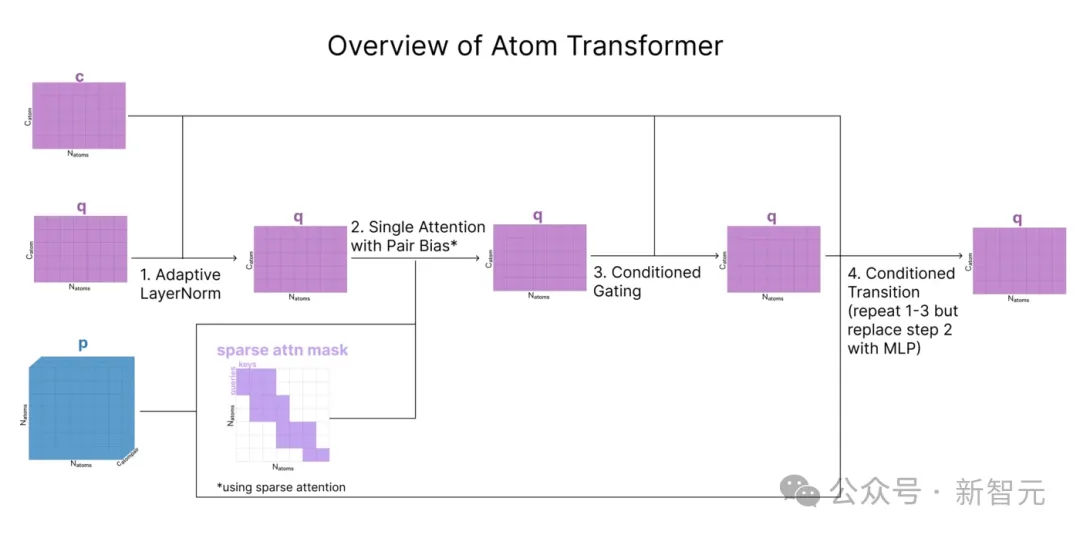
在生成了q（单个原子的表征）和 p（原子配对表征）之后，我们现在要根据附近的其他原子更新这些表征。

AF3使用一个名为原子Transformer的模块，在原子级别应用注意力机制时

原子Transformer主要遵循标准的Transformer结构。不过，其具体步骤都经过了调整，以处理来自c和p的额外输入。

原子级->token级

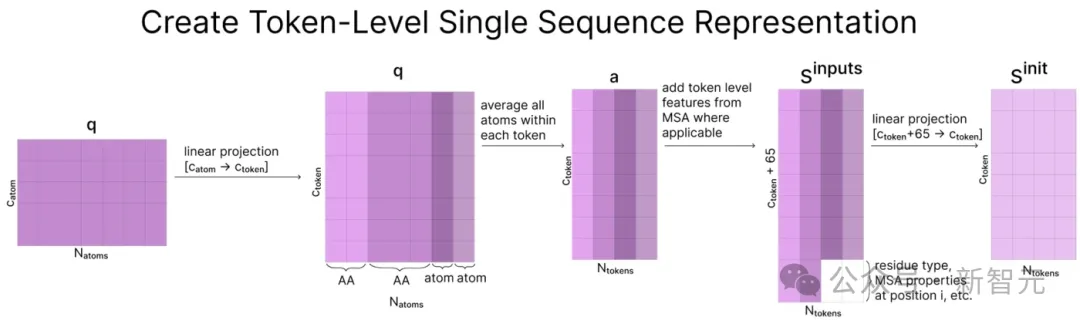
到目前为止，所有数据都是以原子级别存储的，而AF3的表征学习部分则从这里开始以token级别运行。

为了创建token级表征，我们首先将原子级表征投影到一个更大的维度（c_atom=128，c_token=384）。然后对分配给同一token的所有原子取平均值。

请注意，这只适用于与标准氨基酸和核苷酸相关的原子，其余原子保持不变。

现在我们就从「原子空间」进入了「token空间」。

之后将token级特征和MSA中的统计信息连接起来，形成矩阵s^inputs并被向下投影到c_token，作为序列的起始表征s^init。

s^init将在表征学习部分中被更新，但s^inputs保持不变，用于结构预测部分。

表征学习

经过一系列输入准备后，我们就来到了模型的主干部分，也是完成大部分计算量的部分。

这部分模型的学习目标是改进上述token级别的单一（s）或成对（z）张量的初始化表示，因此被称为「表征学习」。

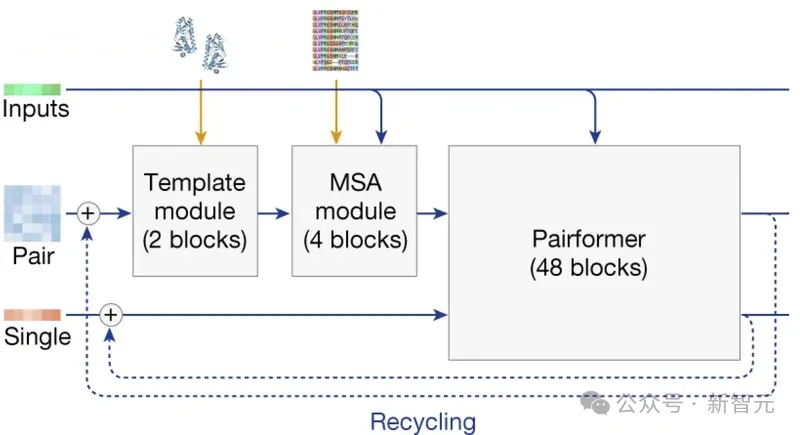
这部分主要包含三类步骤：

- 模板模块（template module）：使用模板t更新张量z

- MSA模块：更新MSA表征m，再将其引入token级别的张量z

- Pairformer：使用三角注意力更新张量s、z

以上步骤会重复运行多次，每次输出结果后再将其反馈到自身继续作为输入，继续进行计算（如上图中蓝色需先所示），这种做法被称为「回收」（recycling）。

模板模块

该模块的计算流程如下图所示（模板个数N_template=2）。

每个模板t和张量z经过线性投影后相加得到矩阵v，再经过一系列被称作Pairformer Stack的操作（后文详述）。

之后，N个模板被平均到一起，再通过另一个线性层和一次ReLU，得到最终结果。

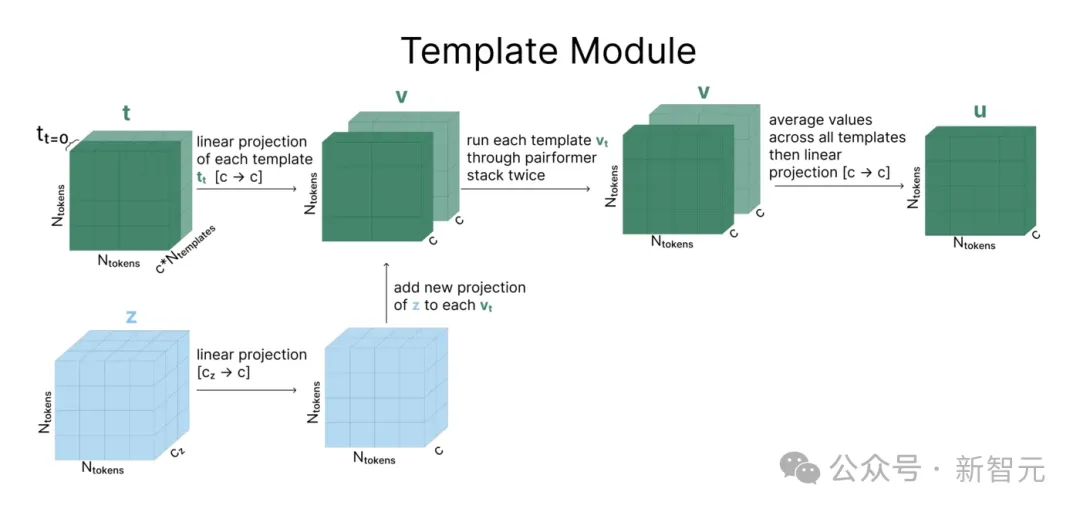
有趣的是，这是AF3模型中唯二使用ReLU的地方之一，但论文中并没有解释为什么选择ReLU而非其他非线性函数。

MSA模块

AF3中的MSA与AF2中的Evoformer非常类似，都是在同时改进MSA表征和配对表征，对两者分别独立执行一系列操作后进行交互。

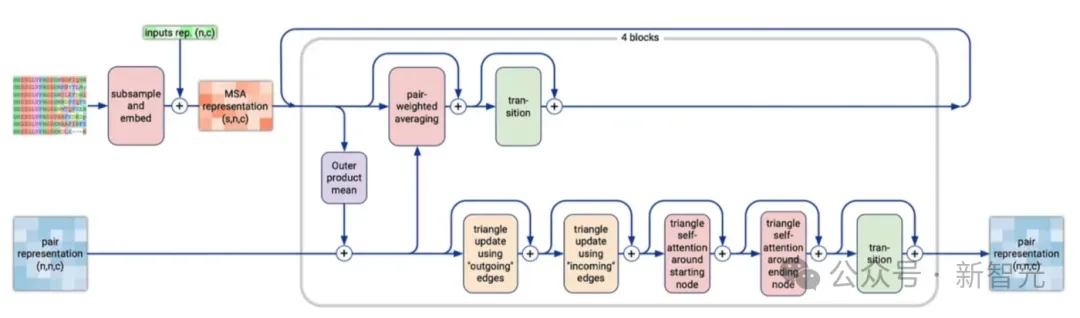
下采样

处理MSA表征的第一步是下采样，而非使用之前生成的MSA的所有行（最多可达 16k）。下采样后，还要加入经过投影映射的单一表征s。

外积均值

之后，MSA表征m通过外积均值方法（outer product mean）被合并到配对表征中。

如下图所示，比较MSA中的两列揭示了有关序列中两个位点之间的关系信息（比如进化过程中的相关性）。

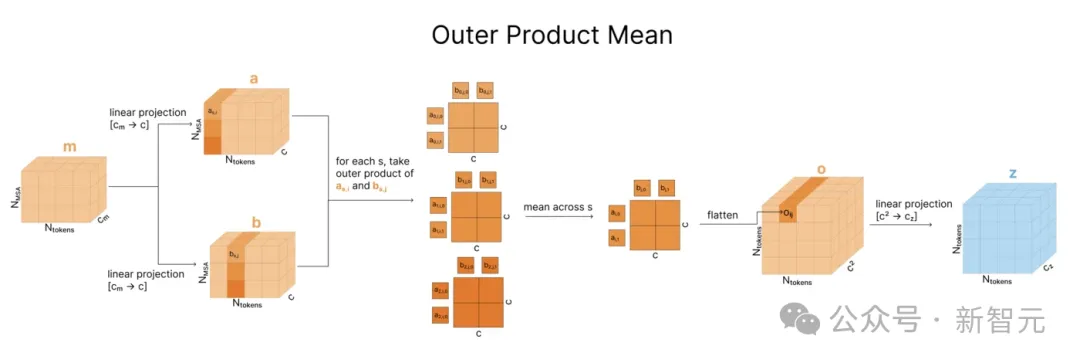
对于每对标记索引i,j，我们迭代所有进化序列s，获取 m_s,i和 m_s,j的外积，在所有进化序列中进行平均。

然后，我们压平这个外部积并将其投影回去，最后将其添加至配对表征z_i,j 。

虽然每个外积仅对给定序列m_s内的值进行操作，但取平均值时会混合序列之间的信息。这是模型中唯一能在进化序列之间共享信息的机制。

这个方法是相对于AF2的重大改变，旨在降低Evoformer的计算复杂度。

行内自注意力

根据MSA更新配对表征后，模型接下来根据后者更新MSA，这种特定的更新模式是原子Transformer中所述的「具有配对偏差的自注意力」的简化版本，被称为「仅使用配对偏差的行内门控自注意力」（row-wise gated self-attention using only pair bias）。

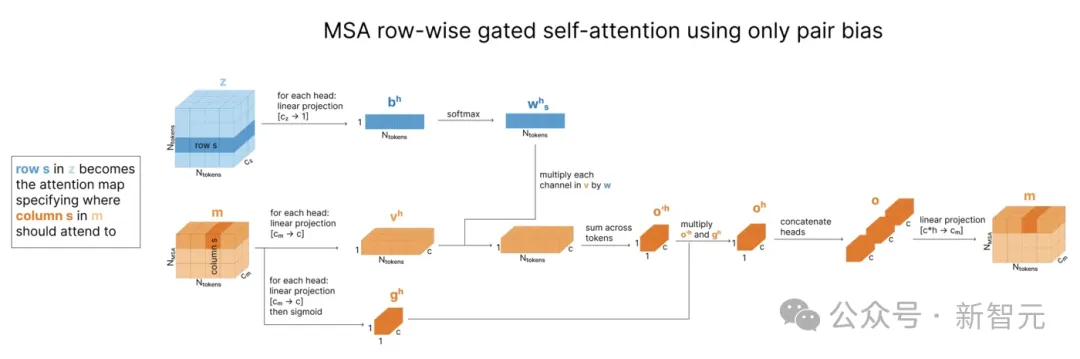
这种方法受到注意力机制的启发，但并不使用查询和键计算，而是直接使用存储在配对表征z中的token间关系。

如下图所示，在张量z中，每个c_z维度的向量z_i,j都表示第i个和第j个token间的关系。将z线性投影到矩阵b后，每个z_i,j向量变为标量，就可以相当于「注意力分数」（attention score），用于加权平均。

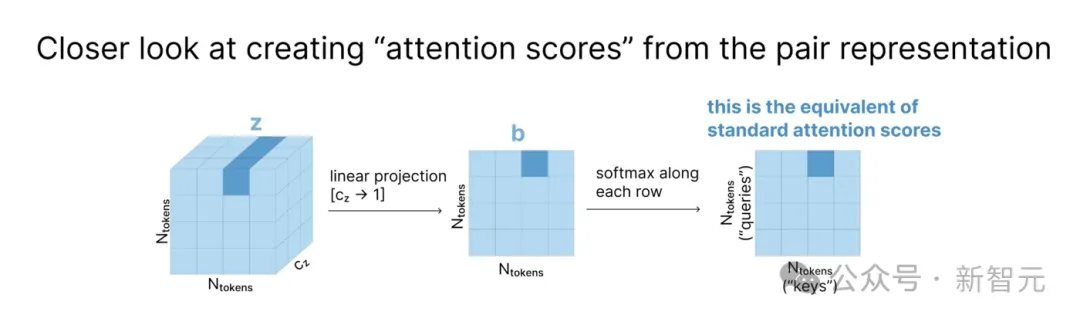
最后，MSA通过一系列「三角更新」（triangle updates）和注意力机制来更新配对表征，其中「三角更新」与下面Pairformer的描述相同。

Pairformer

经过前两个模块后，模板t和MSA表征m的作用就结束了，只有单一表征z和经过更新的配对表征s进入Pairformer并用于相互更新。

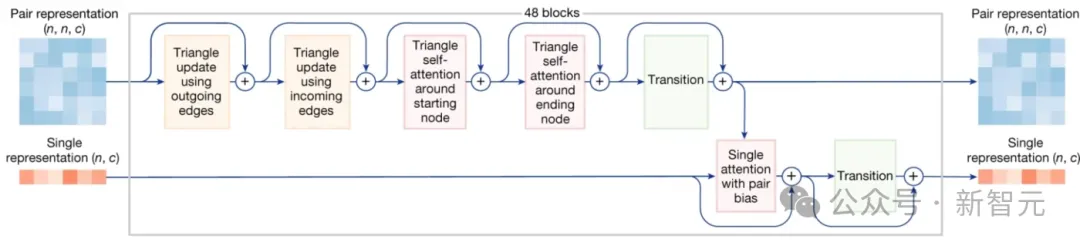
Pairformer中值得注意的是「三角更新」和「三角自注意力」方法，它们首次在AF2模型中出现，并被保留在AF3中，而且正在被应用到越来越多的架构中。

为什么是「三角形」

这里的指导原则是三角形不等式的思想：「三角形任意两边之和大于或等于第三条边。」

回想一下，张量z中的值z_i,j编码序列中位置i和j之间的关系。虽然并没有显式地对token间的物理距离进行编码，但的确包含了这层含义。

如果我们想象每个z_i,j代表两个氨基酸之间的距离，并且有z_i,j=1和z_j,k=1。那么根据三角形不等式，z_i,k不能大于2。

「三角更新」和「三角形自注意力」的目标就是尝试将这些几何约束编码到模型中，但并不会强制执行，而是鼓励模型在每次更新z_i,j的值时考虑所有可能的三元组(i,j,k)。

此外，z不仅代表物理距离，还编码了token之间复杂的物理关系，因此向量z_i,j是有方向的。

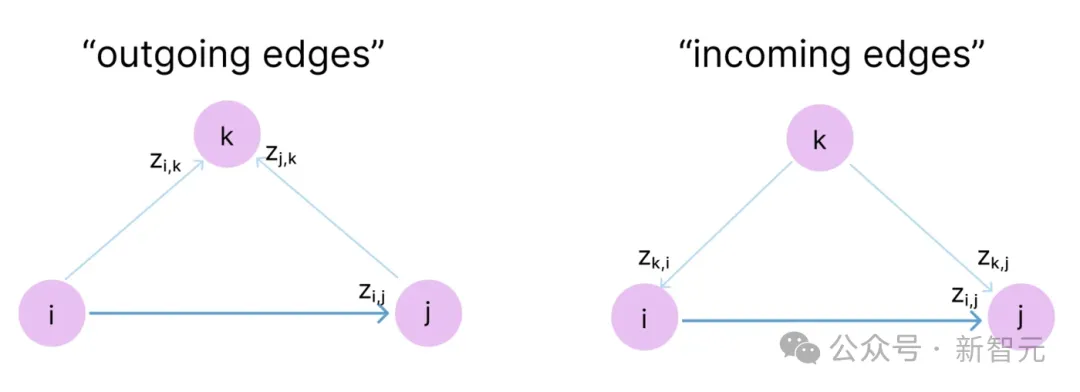
所以，如上图所示，在对节点k进行「三角更新」和「三角自注意力」操作时，需要分别查看两种有向路径，出边（outgoing edge）和入边（incoming edges）。

三角更新

从图论角度理解「三角」操作后，我们就能明白以下的张量更新和注意力机制是如何通过张量运算实现的。

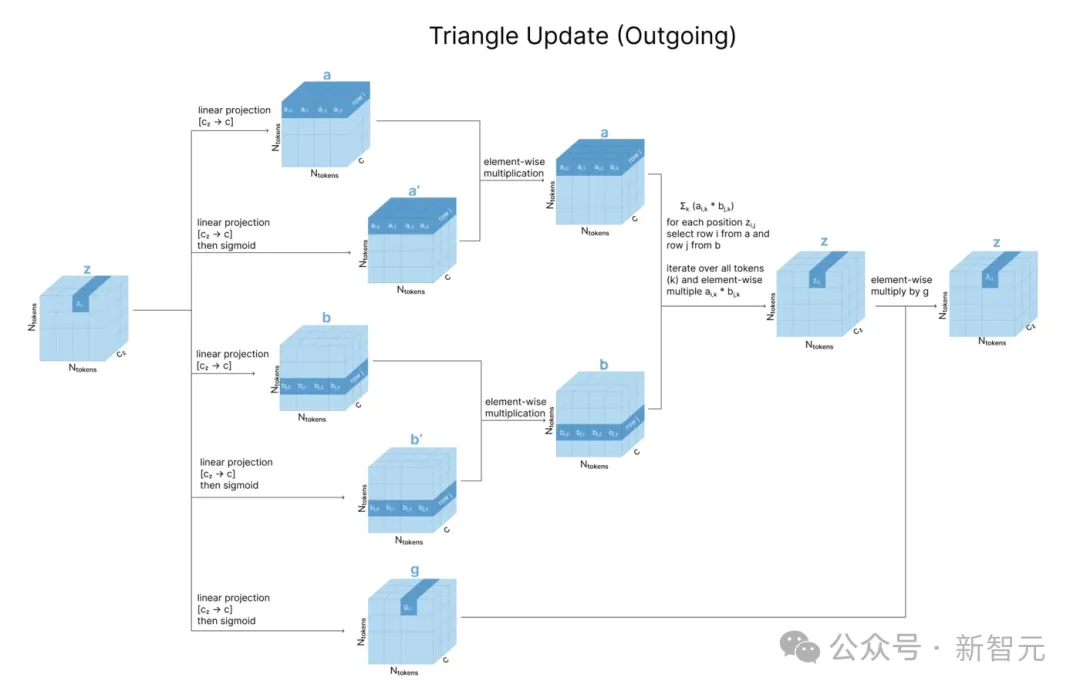
使用出边进行更新时，使用到了z的三个线性投影a、b和g。

为了更新z_i,j，需要对z_i,k和z_j,k进行操作，即对a中的第i行和b中的第j行进行逐元素（element-wise）乘法，之后对所有行（不同k值）求和，再用g进行门控。

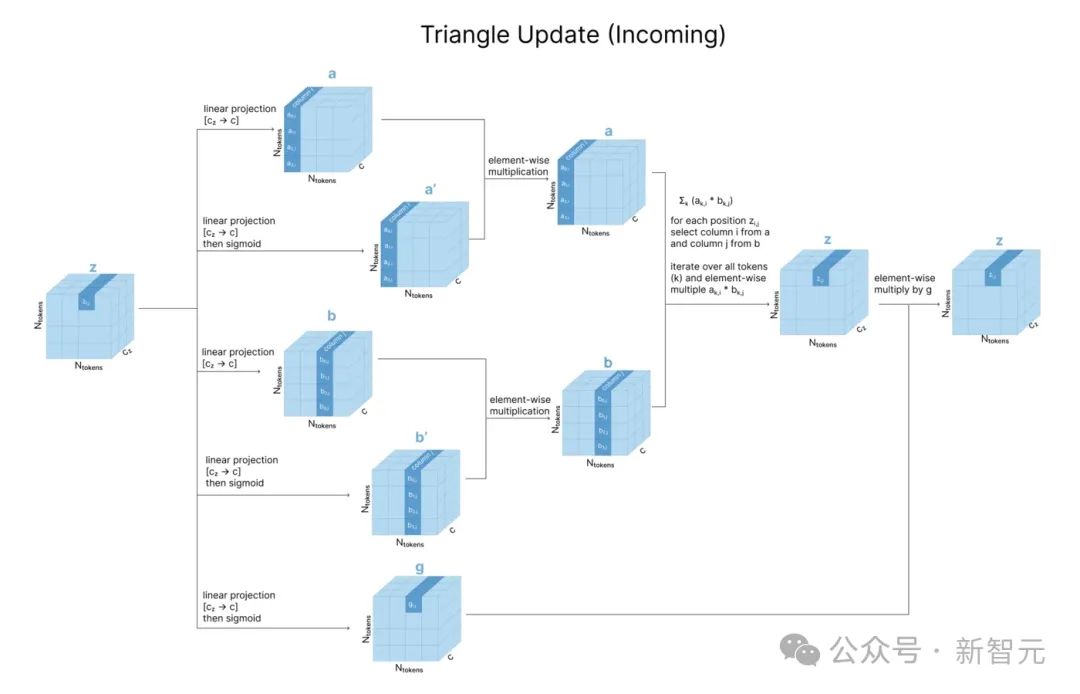
入边的操作与出边类似，只是进行了行列翻转。

为了更新z_i,j，需要对z_k,i和z_k,j进行操作，即对a中的第i列和b中的第j列进行逐元素乘法，再对所有行求和。

可以发现，出边和入边的「三角更新」操作与上面标出有向路径的两个紫色三角形完全对应。

三角自注意力

接下来，分别使用出边和入边的「三角自注意力」更新每个z_i,j值。AF3论文将这两个过程分别称为「围绕起始节点」（around starting node）和「围绕结束节点」（around ending node）。

回忆一下，典型的一维序列自注意力中，查询、键和值都是原始一维序列的转换。自注意力的二维变体——轴向注意力中，在二维矩阵的不同轴上（行，然后列）上独立应用一维自注意力。

以此类推，「三角自注意力」在轴向注意力的基础上添加了之前讨论的「三角形不等式」，通过合并所有k值的z_i,k和z_j,k来更新z_i,j。

比如，在围绕起始节点的情况中（下图），为了计算注意力分数z_i,j，需要将q_i,j与k矩阵中第i行每个值相乘（以确定第j列受到其他列的影响），然后加上z_j,k的注意力偏置。

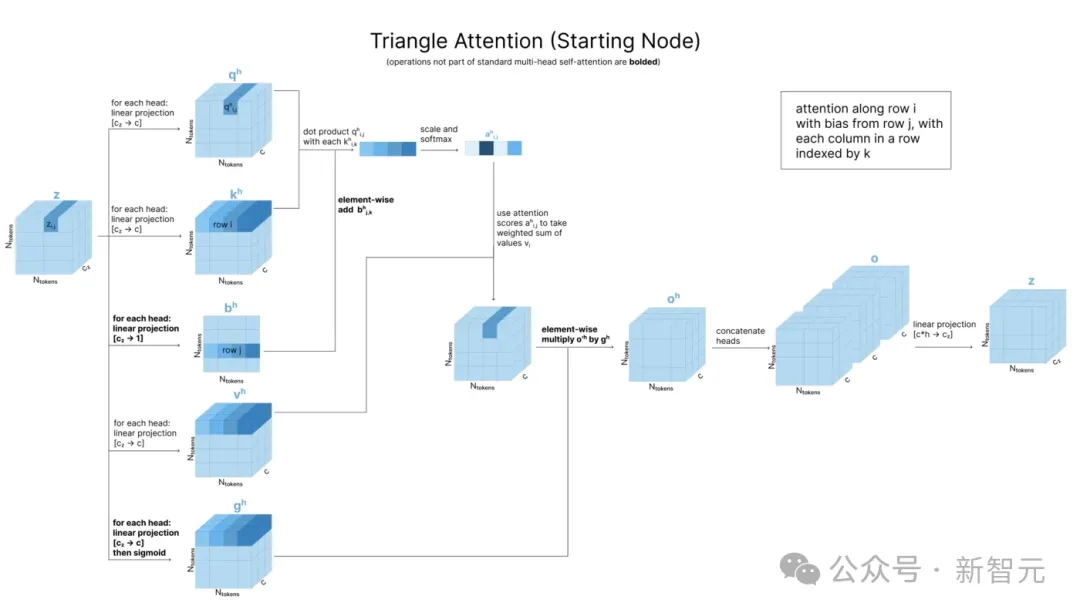
围绕结束节点的情况同样是行列对称，为了计算z_i,j，需要将q_i,j与k矩阵中第i列每个值相乘，注意力偏置则来自第j列。

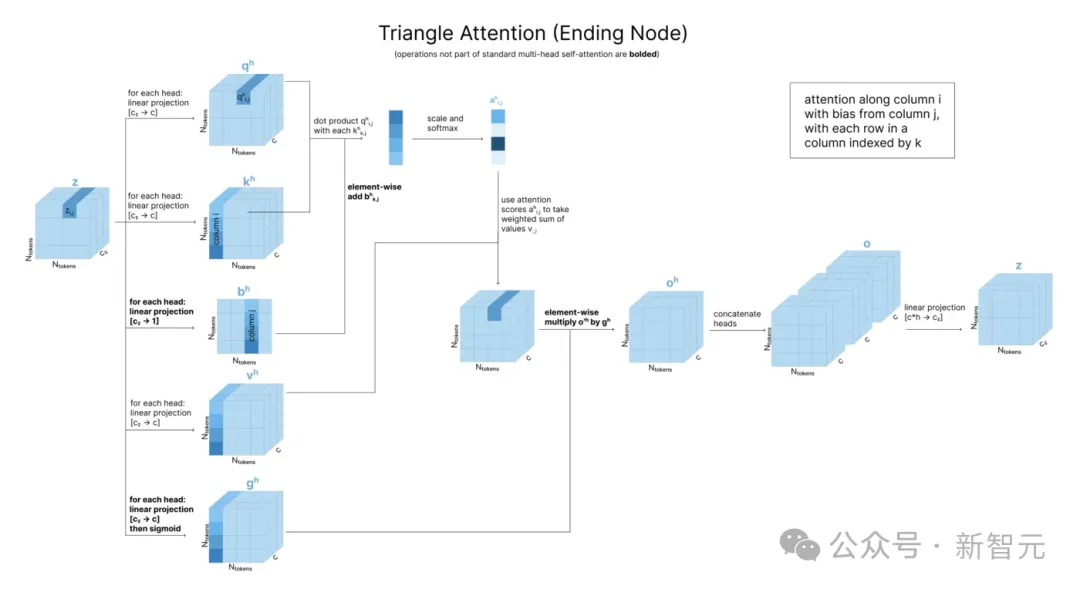
用四个与「三角」有关的步骤更新了配对表征z后，我们还希望用它来更新单一表征s，此处使用的方法是「带有配对偏置的单一注意力」（single attention with pair bias，下图）。

这个方法在输入准备部分的原子Transformer中也被用到，区别只在于一个是token级别，一个是原子级别。

由于在token级别上运行，因此这里用到的是完全注意力，而非块内稀疏模式。

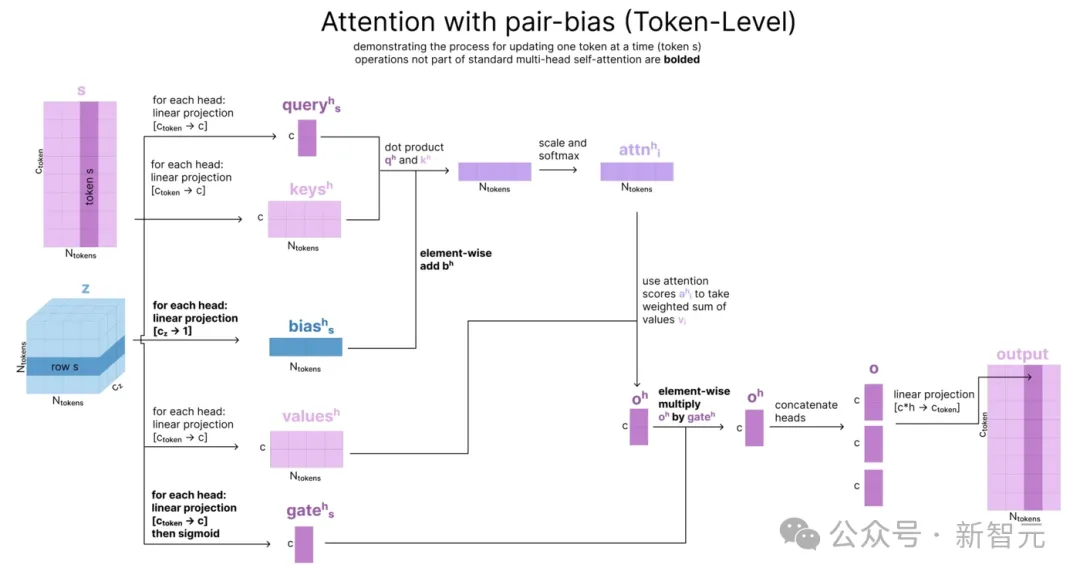
以上是Pairformer的所有计算流程。经过48个块的重复计算后，我们就得到了张量s^trunk和z^trunk。

结构预测

扩散模块

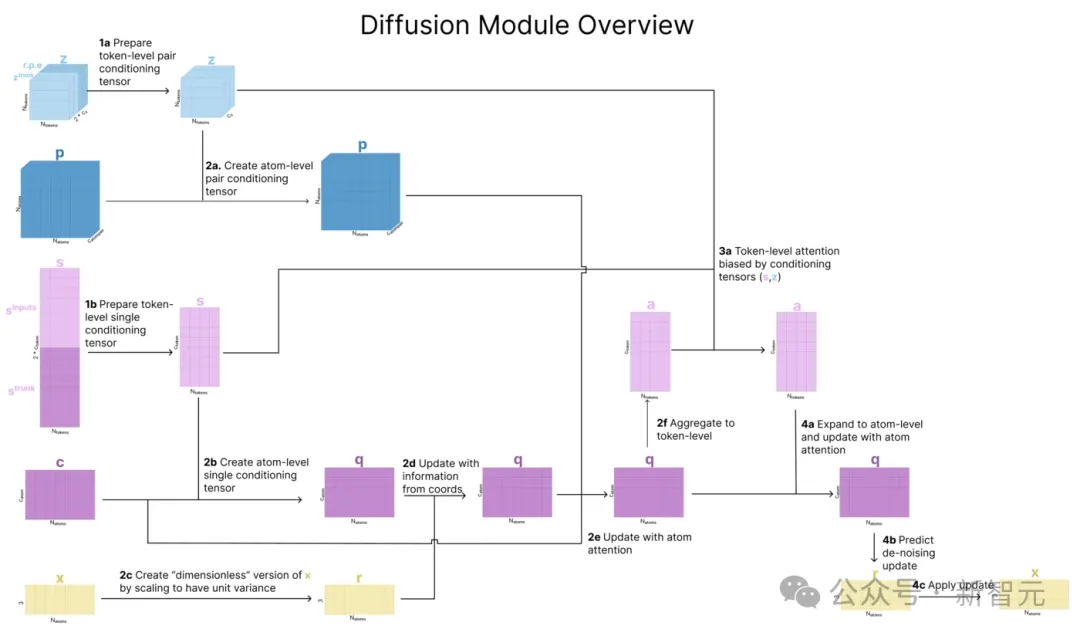
每一个去噪扩散步骤都根据输入序列的多个表征来调整预测。

AF3论文将其扩散过程分为3个步骤，包括从token到原子、回到token、再回到原子。

准备token级条件张量

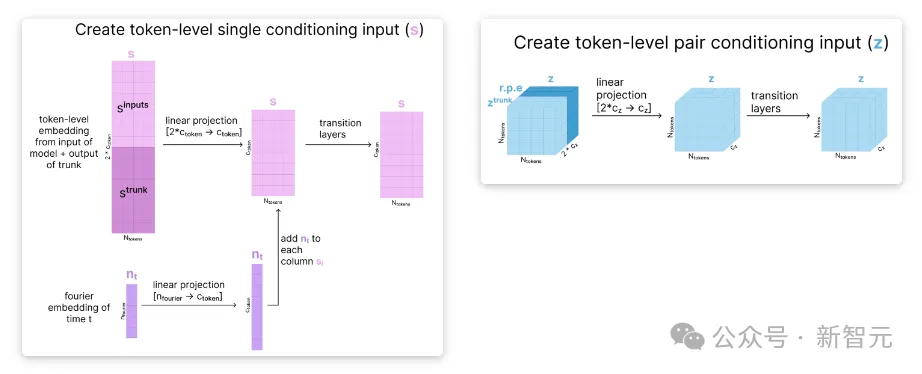
为了初始化token级条件表征，我们将z^trunk与相对位置编码拼接，然后将这个更大的表征向下投影，并通过几个带有残差连接的转换模块。

同样地，对于token级的单一表征，我们将模型的初始表征（s^inputs）和我们当前表征（s^trunk）拼接起来，然后投影回原始大小。

然后，我们根据当前的扩散时间步长创建一个傅立叶编码模型，将其添加到单一表征中，并将该组合通过多个转换模块。

通过在这里的条件输入中加入扩散时间步长，可以确保模型在进行去噪预测时能够意识到扩散过程的时间步长，从而预测出该时间步长下需要消除噪声的合适规模。

准备原子级张量，应用原子级注意力，并聚合回token级

此时，条件向量存储的是每个token级别的信息，但我们还希望在原子级别上运行注意力。

为了解决这个问题，我们采用编码部分（c 和 p）中创建的输入的初始原子级表征，并根据当前的token级表征更新它们，以创建原子级条件张量。

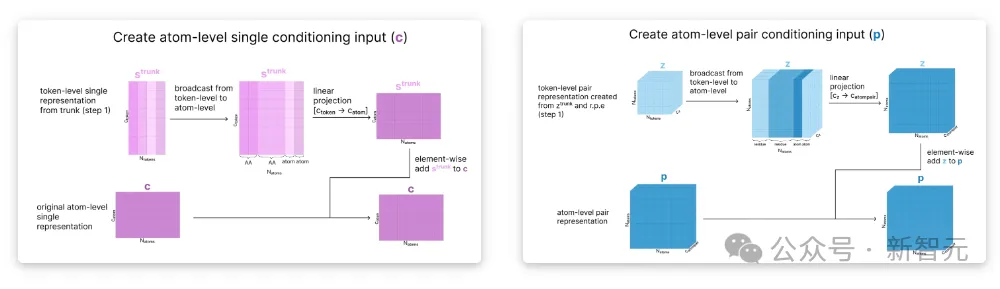
接下来，使用数据方差来缩放原子的当前坐标（x），从而有效地创建出具有单位方差（称为r）的「无量纲」坐标。

然后我们根据r更新q，这样q就包含了原子的当前位置信息。最后，使用原子Transformer更新q，并将原子聚合为我们之前看到的token。

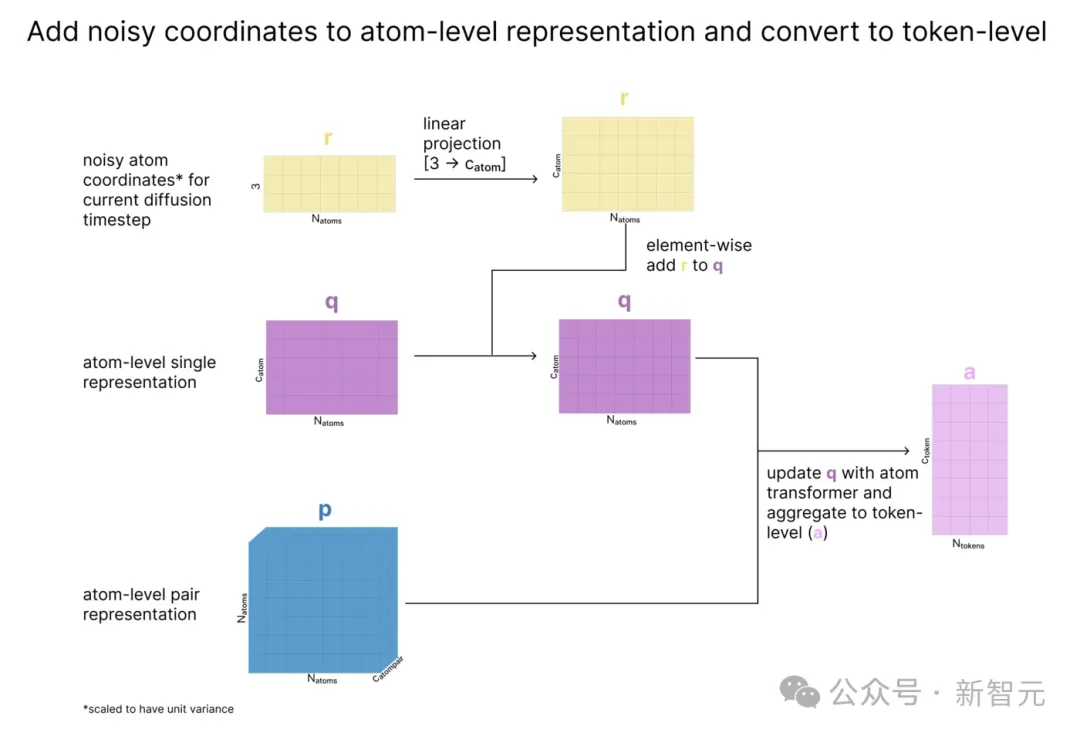
在token级应用注意力机制

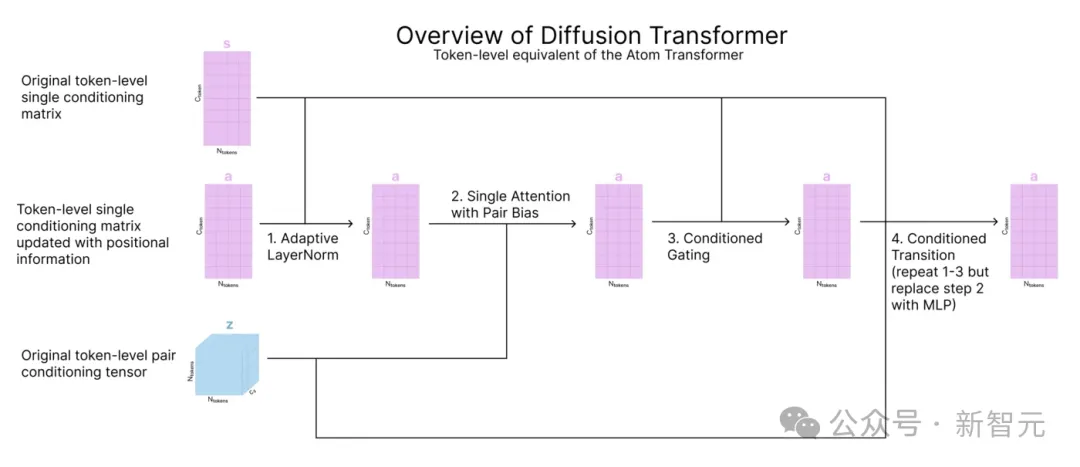
这一步的目标是运用注意力机制更新原子坐标和序列信息的token级表征a。这一步使用的是输入准备过程中可视化的扩散Transformer，它与原子Transformer相同，但针对token。

在原子级应用注意力机制来预测原子级噪声更新

现在，我们回到原子空间，使用原子Transformer和经过更新的a来对q进行更新。

与上一步一样，我们广播token表征，使其与开始时的原子数量相匹配，然后运行原子Transformer。

最重要的是，最后一层线性层将原子级表征q映射回R。这是关键的一步：我们使用所有这些条件表征为所有原子生成坐标更新r^update。

由于是在「无量纲」空间r_l中生成这些更新的，因此需要进行重新缩放，将 r^update中的更新转换为为非单位方差的形式x^update，再引入到x_l中。

至此，我们就完成了对AlphaFold 3主要架构的介绍！

此外，作者还提供了一些有关损失函数机器训练细节的补充信息，好学的朋友可以去博文中一看究竟。

ML工程师眼中的AF3

在对AF3的架构及其与AF2的比较进行了如此详尽的介绍之后，作者没有止步于此，而是将之与更广泛的机器学习趋势相关联，这一点很有意思。

作者提到了AF与检索增强生成、Pair-Bias注意力机制、自监督训练、分类与回归、LSTM循环架构、交叉蒸馏之间的关系。

作者简介

本文作者是来自斯坦福大学的两位博士生Elana Simon和Jake Silberg。

Elana Simon本科从哈佛大学毕业并获得计算机科学领域学士学位，曾在谷歌、Facebook等机构实习，并担任过Reveries Labs的机器学习工程师。

她目前是博士二年级，由James Zou指导，从事机器学习和生物学（免疫学和基因学）交叉领域的研究。

Jake Silberg本科毕业于哈佛大学社会研究专业，辅修全球健康和卫生政策，硕士毕业于斯坦福大学统计系数据科学专业。

他曾在麦肯锡担任高级业务分析师，目前在斯坦福大学攻读生物医学数据科学方面的博士学位，研究兴趣包括主动学习、人机交互，以及Transformer在卫星和医学图像中的应用。