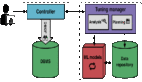
超参数调优是机器学习和深度学习中重要的步骤,旨在选择最佳的超参数组合,以提高模型的性能。

超参数是那些在训练模型之前需要设置的参数,而不是在训练过程中自动学习的参数。
常见的超参数包括学习率、批大小、正则化参数、神经网络的层数和每层的神经元数等。

常见的超参数调优技术
1.网格搜索
网格搜索是一种穷举搜索技术,用于系统地遍历多种参数组合,以找到最佳的模型参数。
这种方法简单直接,但计算成本可能较高,尤其是当参数空间较大时。

优点:
- 简单易懂:网格搜索直观易理解,适用于参数数量较少时。
- 彻底性:可以保证在给定的参数网格内找到最优的组合。
缺点:
- 计算成本高:当参数空间大或者模型复杂时,计算成本非常高,因为它需要评估所有可能的参数组合。
代码示例
from sklearn.model_selection import GridSearchCV
from sklearn.ensemble import RandomForestClassifier
import numpy as np
# 定义模型
model = RandomForestClassifier()
# 定义参数网格
param_grid = {
'n_estimators': [50, 100, 200],
'max_features': ['auto', 'sqrt', 'log2'],
'max_depth': [None, 10, 20, 30]
}
# 创建网格搜索对象
grid_search = GridSearchCV(estimator=model, param_grid=param_grid, cv=3, scoring='accuracy')
# 拟合网格搜索
grid_search.fit(X_train, y_train)
# 最优参数和最优得分
print("最优参数:", grid_search.best_params_)
print("最高得分:", grid_search.best_score_)2.随机搜索
随机搜索不像网格搜索那样尝试所有可能的组合,而是在参数空间中随机选取参数组合。
这种方法可以在更大的参数空间内更快地找到不错的解。

优点:
- 高效:在大参数空间中比网格搜索更加高效,不需要测试所有可能的参数组合。
缺点:
- 无保证:由于其随机性,不能保证找到全局最优解,特别是在迭代次数有限的情况下。
- 结果的随机性: 同样的参数和设置可能导致不同的搜索结果。
代码示例
from sklearn.model_selection import RandomizedSearchCV
from sklearn.ensemble import RandomForestClassifier
# 定义模型
model = RandomForestClassifier()
# 定义参数分布
param_dist = {
'n_estimators': [50, 100, 200, 300],
'max_features': ['auto', 'sqrt', 'log2'],
'max_depth': [None, 10, 20, 30, 40]
}
# 创建随机搜索对象
random_search = RandomizedSearchCV(estimator=model, param_distributinotallow=param_dist, n_iter=100, cv=3, scoring='accuracy')
# 拟合随机搜索
random_search.fit(X_train, y_train)
# 最优参数和最优得分
print("最优参数:", random_search.best_params_)
print("最高得分:", random_search.best_score_)3.贝叶斯优化
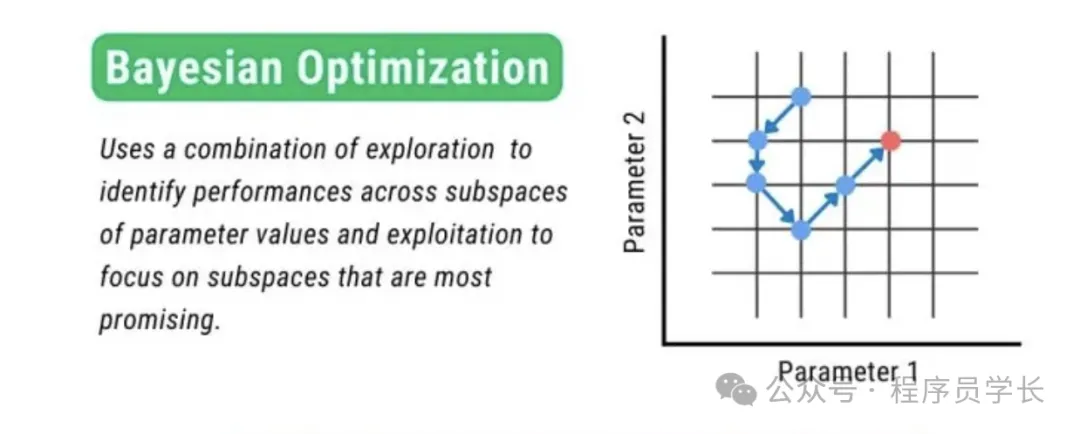
贝叶斯优化是一种高效的全局优化技术,广泛用于机器学习领域中模型超参数的调优。
这种方法利用贝叶斯统计理论,通过构建一个代理模型(通常是高斯过程)来预测目标函数的表现,并基于这个模型进行决策,以选择新的参数值来测试。
优点:
- 高效且有效:在较少的函数评估次数内找到最优解,适用于评估代价高的情况。
- 适用于复杂空间:可以很好地处理非凸的优化问题。
缺点:
- 实现复杂:相对于网格搜索和随机搜索,贝叶斯优化算法的实现和调试更为复杂。
- 计算密集型:在每一步都需要更新代理模型,可能需要高昂的计算成本,尤其是在参数维度非常高的情况下。
代码示例
from bayes_opt import BayesianOptimization
from sklearn.model_selection import cross_val_score
from sklearn.ensemble import RandomForestClassifier
# 定义目标函数
def rf_cv(n_estimators, max_features, max_depth):
estimator = RandomForestClassifier(
n_estimators=int(n_estimators),
max_features=min(max_features, 0.999), # 浮点类型
max_depth=int(max_depth),
random_state=2
)
cval = cross_val_score(estimator, X_train, y_train, scoring='accuracy', cv=5)
return cval.mean()
# 定义参数范围
pbounds = {
'n_estimators': (50, 300),
'max_features': (0.1, 0.999),
'max_depth': (5, 50)
}
# 初始化贝叶斯优化
optimizer = BayesianOptimization(f=rf_cv, pbounds=pbounds, random_state=1)
# 执行优化
optimizer.maximize(init_points=2, n_iter=10)
# 输出最优参数
print("最优参数:", optimizer.max['params'])4.Hyperband
Hyperband 是一种基于多武装赌博机的优化技术,利用资源分配和早期停止策略来快速找到最优参数。
这种方法主要适用于需要大量计算资源的情况,如大规模深度学习模型训练。
优点:
- 快速且高效: 通过早期停止低效的模型来节省时间和资源,使得它在处理需要大量资源的训练任务时特别有效。
- 动态资源分配:可以更智能地分配计算资源,优先给予表现良好的配置更多的资源。
缺点:
- 依赖于早期表现:基于早期停止策略,可能会错过最初表现不佳但最终可能优化良好的配置。
- 实现复杂性:相较于其他方法,Hyperband 的实现更为复杂,需要对资源管理和调度有较好的控制。
代码示例
在这个例子中,我们定义了一个简单的神经网络,并用 Hyperband 算法来调整网络中的隐藏层单元数和学习率。
此外,我们使用了 Fashion MNIST 数据集来训练和验证模型。
import tensorflow as tf
from tensorflow import keras
from tensorflow.keras import layers
from kerastuner.tuners import Hyperband
def build_model(hp):
model = keras.Sequential()
model.add(layers.Flatten(input_shape=(28, 28)))
# 使用hp.Int()来定义学习的参数
model.add(layers.Dense(units=hp.Int('units', min_value=32, max_value=512, step=32), activatinotallow='relu'))
model.add(layers.Dense(10, activatinotallow='softmax'))
model.compile(
optimizer=keras.optimizers.Adam(
hp.Choice('learning_rate', [1e-2, 1e-3, 1e-4])),
loss='sparse_categorical_crossentropy',
metrics=['accuracy'])
return model
# 加载数据
(x_train, y_train), (x_test, y_test) = keras.datasets.fashion_mnist.load_data()
x_train = x_train.astype('float32') / 255
x_test = x_test.astype('float32') / 255
# 初始化Hyperband调优器
tuner = Hyperband(
build_model,
objective='val_accuracy',
max_epochs=40,
directory='my_dir',
project_name='hyperband_tuning'
)
# 执行超参数搜索
tuner.search(x_train, y_train, epochs=10, validation_split=0.2)
# 获取最优模型
best_model = tuner.get_best_models(num_models=1)[0]
best_model.evaluate(x_test, y_test)