AI 已经在帮助数学家和科学家做研究了，比如著名数学家陶哲轩就曾多次分享自己借助 GPT 等 AI 工具研究探索的经历。AI 要在这些领域大战拳脚，强大可靠的因果推理能力是必不可少的。
本文要介绍的这项研究发现：在小图谱的因果传递性公理演示上训练的 Transformer 模型可以泛化用于大图谱的传递性公理。
也就是说，如果让 Transformer 学会执行简单的因果推理，就可能将其用于更为复杂的因果推理。该团队提出的公理训练框架是一种基于被动数据来学习因果推理的新范式，只有演示足够就能用于学习任意公理。
引言
因果推理（causal reasoning）可以定义成一组推理流程并且这组推理流程要符合专门针对因果性的预定义公理或规则。举个例子，d-separation（有向分离）和 do-calculus 规则可被视为公理，而 collider set 或 backdoor set 的规范则可被看作是由公理推导出的规则。
通常来说，因果推理使用的数据对应于一个系统中的变量。通过正则化、模型架构或特定的变量选择，可以归纳偏置的形式将公理或规则集成到机器学习模型中。
根据可用数据种类的差异（观察数据、干预数据、反事实数据），Judea Pearl 提出的「因果阶梯」定义了因果推理的可能类型。
由于公理是因果性的基石，因此我们不禁会想是否可以直接使用机器学习模型来学习公理。也就是说，如果学习公理的方式不是学习通过某个数据生成流程得到的数据，而是直接学习公理的符号演示（并由此学习因果推理），哪又会如何呢？
相较于使用特定的数据分布构建的针对特定任务的因果模型，这样的模型有一个优势：其可在多种不同的下游场景中实现因果推理。随着语言模型具备了学习以自然语言表达的符号数据的能力，这个问题也就变得非常重要了。
事实上，近期已有一些研究通过创建以自然语言编码因果推理问题的基准，评估了大型语言模型（LLM）是否能够执行因果推理。
微软、MIT 和印度理工学院海得拉巴分校（IIT Hyderabad）的研究团队也朝这个方向迈出了重要一步：提出了一种通过公理训练（axiomatic training）学习因果推理的方法。
- 论文标题：Teaching Transformers Causal Reasoning through Axiomatic Training
- 论文地址：https://arxiv.org/pdf/2407.07612
公理训练
他们假设，可将因果公理表示成以下符号元组 ⟨premise, hypothesis, result⟩。其中 hypothesis 是指假设，即因果陈述；premise 是前提，是指用于确定该陈述是否为「真」的任意相关信息；result 自然就是结果了。结果可以是简单的「是」或「否」。
举个例子，来自论文《Can large language models infer causation from correlation?》的 collider 公理可以表示成：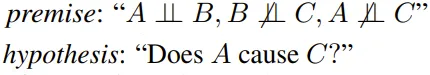
，结论就为「是」。
基于这个模板，可通过修改变量名称、变量数量和变量顺序等来生成大量合成元组。
为了用 Transformer 学习因果公理，实现公理训练，该团队采用了以下方法构建数据集、损失函数和位置嵌入。
公理训练：数据集、损失函数和位置编制
训练数据
基于一个特定公理，可根据「前提」将「假设」映射成合适的标签（Yes 或 No）。要创建训练数据集，该团队的做法是在特定的变量设置 X、Y、Z、A 下枚举所有可能的元组 {(P, H, L)}_N，其中 P 是前提，H 是假设，L 是标签（Yes 或 No）。
给定一个基于某个因果图谱的前提 P，如果可通过使用特定的公理（一次或多次）推导出假设 P，那么标签 L 就为 Yes；否则为 No。
举个例子，假设一个系统的底层真实因果图谱具有链式的拓扑结构：X_1 → X_2 → X_3 →・・・→ X_n。那么，可能的前提是 X_1 → X_2 ∧ X_2 → X_3，那么假设 X_1 → X_3 有标签 Yes，而另一个假设 X_3 → X_1 有标签 No。上述公理可被归纳式地多次用于生成更复杂的训练元组。
对于训练设置，使用传递性公理生成的 N 个公理实例构建一个合成数据集 D。D 中的每个实例都构建成了 (P_i, H_ij, L_ij) 的形式，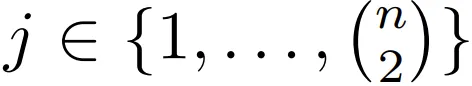
，其中 n 是每第 i 个前提中的节点数量。P 是前提，即某种因果结构的自然语言表达（如 X 导致 Y，Y 导致 Z）；之后是问题 H（如 X 导致 Y 吗？）；L 为标签（Yes 或 No）。该形式能有效覆盖给定因果图谱中每条独特链的所有成对节点。
损失函数
给定一个数据集，损失函数的定义基于每个元组的基本真值标签，表示为：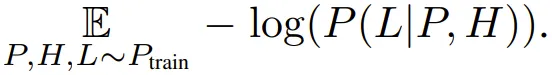
分析表明，相比于下一 token 预测，使用该损失能得到很有希望的结果。
位置编码
除了训练和损失函数，位置编码的选择也是另一个重要因素。位置编码能提供 token 在序列中绝对和相对位置的关键信息。
著名论文《Attention is all you need》中提出了一种使用周期函数（正弦或余弦函数）来初始化这些编码的绝对位置编码策略。
绝对位置编码能为任何序列长度的所有位置提供确定的值。但是，有研究表明绝对位置编码难以应对 Transformer 的长度泛化任务。在可学习的 APE 变体中，每个位置嵌入都是随机初始化的，并使用该模型完成了训练。该方法难以应对比训练时的序列更长的序列，因为新的位置嵌入依然未被训练和初始化。
有趣的是，近期有发现表明移除自回归模型中的位置嵌入可以提升模型的长度泛化能力，而自回归解码期间的注意力机制足以编码位置信息。该团队使用了不同的位置编码来理解其对因果任务中的泛化的影响，包括可学习位置编码（LPE）、正弦位置编码（SPE）、无位置编码（NoPE）。
为了提升模型的泛化能力，该团队也采用了数据扰动，其中包括长度、节点名称、链顺序和分支情况的扰动。
实验
下面问题又来了：如果使用这些数据训练一个模型，那么该模型能否学会将该公理应用于新场景？
为了解答这个问题，该团队使用这个因果无关型公理的符号演示从头开始训练了一个 Transformer 模型。
为了评估其泛化性能，他们在简单的大小为 3-6 个节点的因果无关公理链上进行了训练，然后测试了泛化性能的多个不同方面，包括长度泛化性能（大小 7-15 的链）、名称泛化性能（更长的变量名）、顺序泛化性能（带有反向的边或混洗节点的链）、结构泛化性能（带有分支的图谱）。图 1 给出了评估 Transformer 的结构泛化的方式。
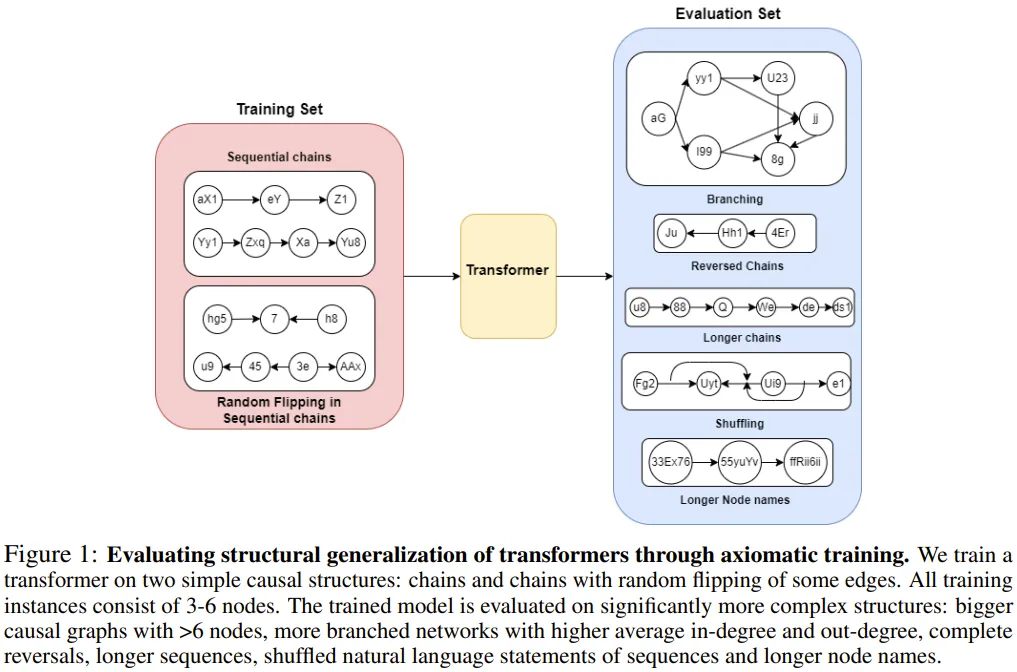
具体来说，他们基于 GPT-2 架构训练了一个基于解码器的有 6700 万参数的模型。该模型有 12 个注意力层、8 个注意力头和 512 嵌入维度。他们在每个训练数据集上从头开始训练了该模型。为了理解位置嵌入的影响，他们还研究了三种位置嵌入设置：正弦位置编码（SPE）、可学习位置编码（LPE）和无位置编码（NoPE）。
结果如表 1、图 3 和图 4 所示。
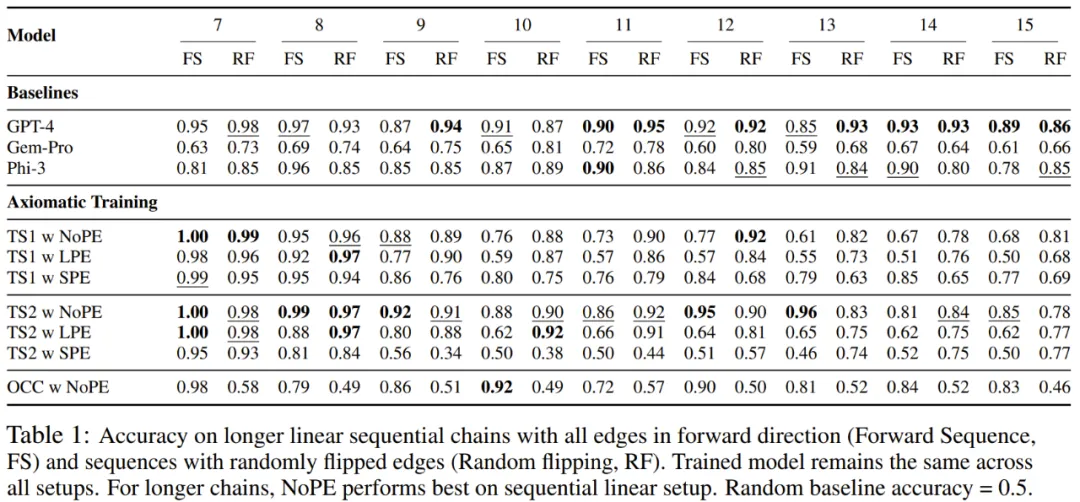
表 1 给出了在训练时未曾见过的更大因果链上评估时不同模型的准确度。可以看到，新模型 TS2 (NoPE) 的表现能与万亿参数规模的 GPT-4 相媲美。
图 3 是在有更长节点名称（长于训练集的）的因果序列上的泛化能力评估结果以及不同位置嵌入的影响。
图 4 评估的是在更长的未见过的因果序列上的泛化能力。
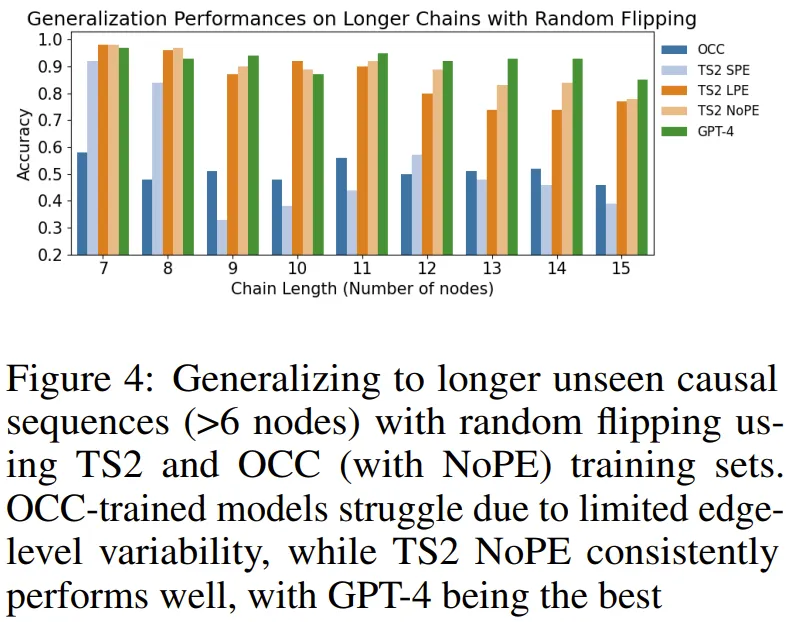
他们发现，在简单链上训练的模型可以泛化到在更大的链上多次应用公理，但却无法泛化到顺序或结构泛化等更复杂的场景。但是，如果在简单链以及带有随机逆向边的链组成的混合数据集上训练模型，则模型可以很好地泛化到各种评估场景。
通过扩展在 NLP 任务上的长度泛化研究结果，他们发现了位置嵌入在确保在长度和其它方面实现因果泛化的重要性。他们表现最佳的模型没有位置编码，但他们也发现正弦编码在某些情况下也很好用。
这种公理训练方法还能泛化用于一个更困难的问题，如图 5 所示。即以包含统计独立性陈述的前提为基础，任务目标是根据因果关系分辨相关性。解决该任务需要多个公理的知识，包括 d-separation 和马尔可夫性质。
该团队使用与上面一样的方法生成了合成训练数据，然后训练了一个模型，结果发现在包含 3-4 个变量的任务演示上训练得到的 Transformer 能学会解决包含 5 个变量的图谱任务。并且在该任务上，该模型的准确度高于 GPT-4 和 Gemini Pro 等更大型的 LLM。
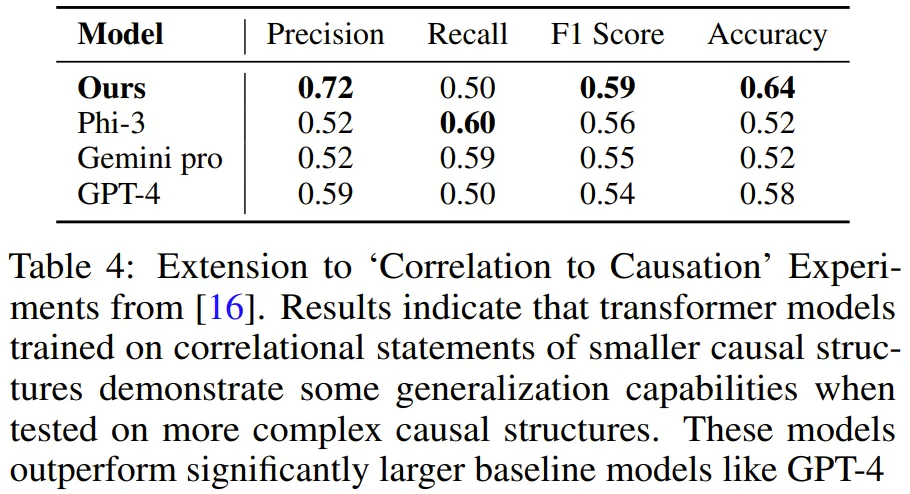
该团队表示：「我们的研究提供了一种通过公理的符号演示教模型学习因果推理的新范式，我们称之为公理训练（axiomatic training）。」该方法的数据生成和训练流程是普适的：只要一个公理能被表示成符号元组的格式，就可使用此方法学习它。
