一文带您了解伪对数(Pseudo-Log)：可视化倾斜数据的黄金方法-51CTO.COM

偏斜数据是指分布高度不均匀的数据：当变量数据显示为直方图时，大部分数据点要么聚集在分布的左侧，长尾向右延伸（右偏斜），要么反之（左偏斜），或呈现更复杂的偏斜模式。偏斜数据对可视化，特别是热力图的绘制，提出了很大的挑战。通常情况下，人们会使用对数变换来处理这些数据。然而，经典对数变换无法处理零或负数，而伪对数变换则能够更好地处理和可视化这些数据。

为什么使用伪对数？

经典对数对零和负值无定义，这限制了其在许多应用中的使用。相比之下，伪对数(Pseudo-Logarithm)修正了经典对数的这一限制：它对所有实数都有定义，对于大绝对值使用带符号的对数，并在底数趋近于零时平滑过渡到零。

以10为底的伪对数（pseudo-log10）的定义是：

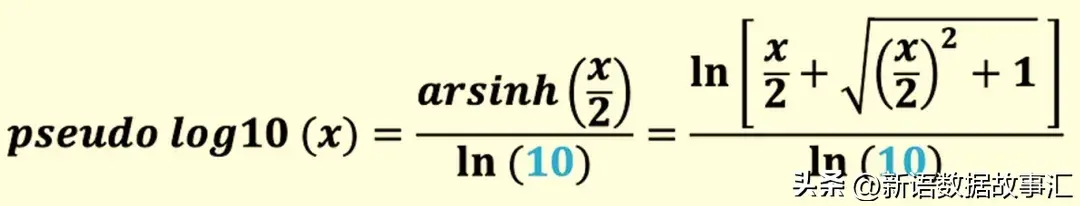
在下面的代码和图中，x轴上的值通过伪对数10变换映射到y轴上，用蓝线表示。相比之下，经典的对数10变换则用黑线绘制。

import numpy as np
import matplotlib.pyplot as plt


# 伪对数10变换函数
def pseudo_log10(x):
    return np.log(x/2+np.sqrt(x*x/4+1))/np.log(10)


# 定义数据
x = np.linspace(-15, 15, 400)
y_pseudo_log10 = pseudo_log10(x)
y_log10 = np.log10(x[200:])  


# 创建图形
plt.figure(figsize=(10, 6))


# 绘制伪对数10变换的曲线，绘制经典对数10变换的曲线
plt.plot(x, y_pseudo_log10, label='Pseudo-log10 Transformation', color='blue')
plt.plot(x[200:], y_log10, label='Classic log10 Transformation', color='black')


# 添加图例
plt.legend()


# 添加标题和标签
plt.title('Comparison of Pseudo-log10 and Classic log10 Transformations')
plt.xlabel('x')
plt.ylabel('Transformed value')


# 显示图形
plt.grid(True)
plt.show()

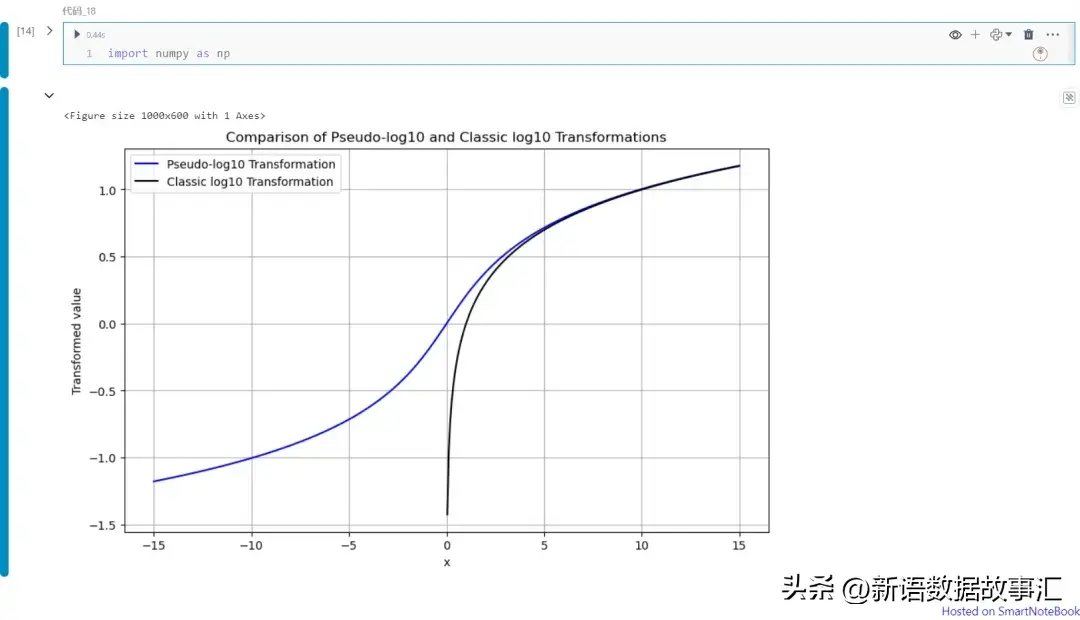
该图展示了伪对数变换的一些良好特性：

伪 log10(x) 在所有实数上都有定义。
伪 log10(0) = 0
如果 x ≫ 0，则伪 log10(x) ≈ log10(x)
如果 x ≪ 0，则伪 log10(x) ≈ −log10(|x|)

类似地，任何底数为b的伪对数（伪对数b）可定义如下：

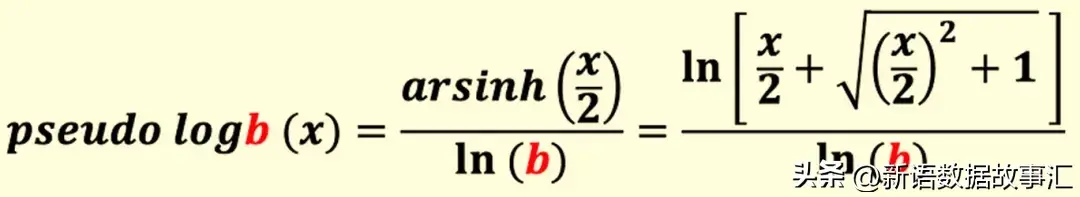
伪对数b (x) 具有以下性质：

伪对数b (0) = 0
如果 x ≫ 0，则伪对数b (x) ≈ log b (x)
如果 x ≪ 0，则伪对数b (x) ≈ −log b (|x|)

数据可视化中的伪对数

对数变换是处理广泛分布数据的常用方法。它将数据转换为更规范的分布，从而更容易可视化。我们先看一下对数变换和伪对数变换对分布的影响（没有找到合适的数据，下面数据是生成的）：

import numpy as np
import matplotlib.pyplot as plt


# 生成1000个来自右偏分布的样本
data = np.random.exponential(scale=2, size=1000)


# 定义伪对数变换函数
def pseudo_log(x):
    return np.log(x/2+np.sqrt(x*x/4+1))/np.log(10)


# 对数据应用变换
log_data = np.log(data)
pseudo_log_data = pseudo_log(data)


# 绘制原始数据、对数变换数据和伪对数变换数据
plt.figure(figsize=(12, 8))


# 绘制原始数据
plt.subplot(3, 1, 1)
plt.hist(data, bins=50, color='blue', alpha=0.7, label='Original Data')
plt.legend()
plt.title('Original Data')


# 绘制对数变换数据
plt.subplot(3, 1, 2)
plt.hist(log_data, bins=50, color='green', alpha=0.7, label='Log-Transformed Data')
plt.legend()
plt.title('Log-Transformed Data')


# 绘制伪对数变换数据
plt.subplot(3, 1, 3)
plt.hist(pseudo_log_data, bins=50, color='red', alpha=0.7, label='Pseudo-Log-Transformed Data')
plt.legend()
plt.title('Pseudo-Log-Transformed Data')


plt.tight_layout()
plt.show()

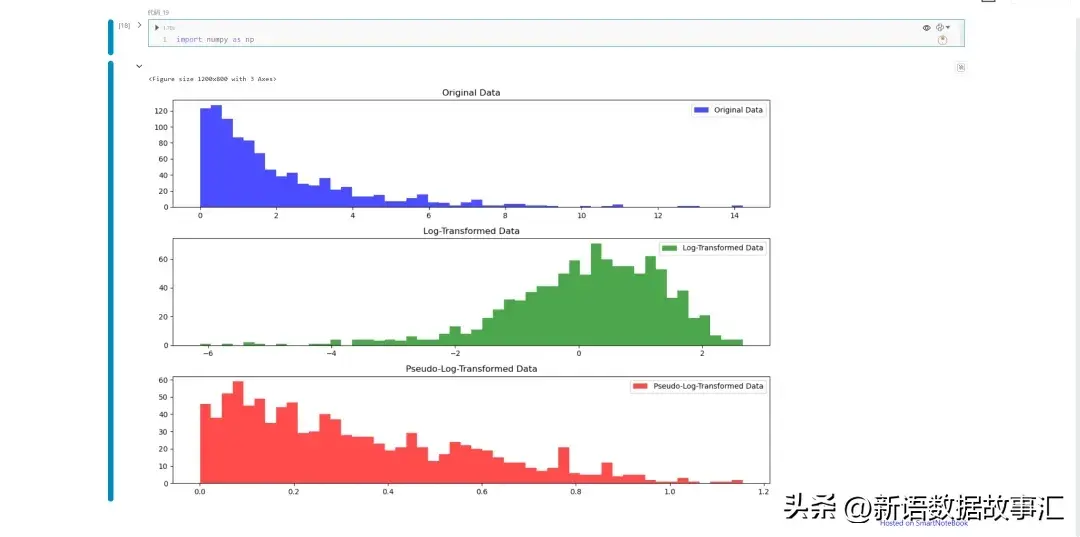
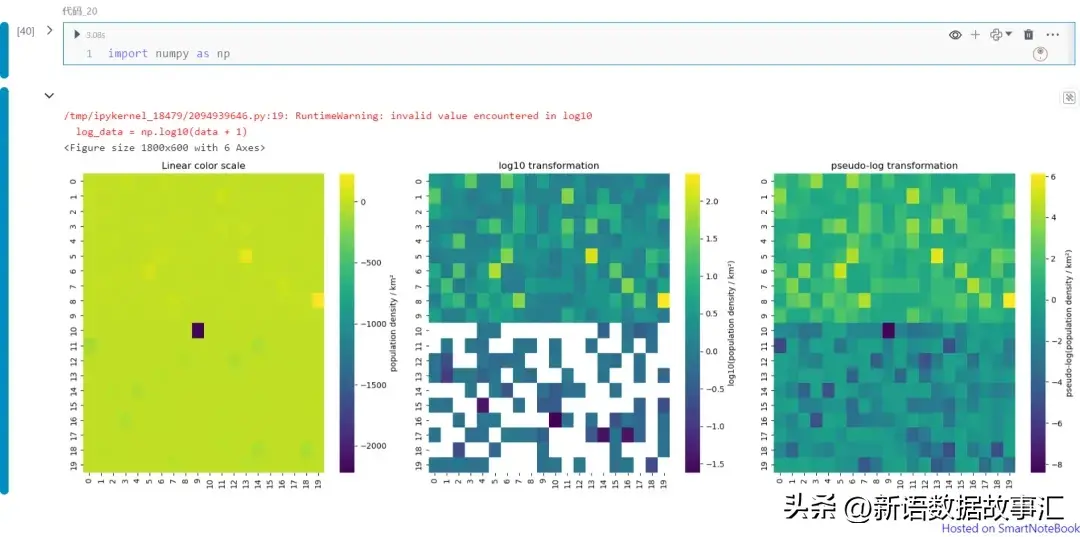
伪对数变换对热力图可视化的效果影响：

import numpy as np
import matplotlib.pyplot as plt
import seaborn as sns


# Simulate some population density data with a wider range
np.random.seed(42)
data = np.concatenate([np.random.lognormal(mean=0, sigma=2.0, size=(10, 20)), 
                       0-np.random.lognormal(mean=0, sigma=2.0, size=(10, 20))])


# Function to plot the heatmaps
def plot_heatmaps(data):
    fig, axes = plt.subplots(1, 3, figsize=(18, 6))
    
    # Linear color scale
    sns.heatmap(data, ax=axes[0], cmap='viridis', cbar_kws={'label': 'population density / km²'})
    axes[0].set_title('Linear color scale')


    # Log10 transformation
    log_data = np.log10(data + 1)
    sns.heatmap(log_data, ax=axes[1], cmap='viridis', cbar_kws={'label': 'log10(population density / km²)'})
    axes[1].set_title('log10 transformation')
    
    # Pseudo-log transformation (log + sqrt)
    pseudo_log_data = np.log(data + np.sqrt(data**2 + 1))
    sns.heatmap(pseudo_log_data, ax=axes[2], cmap='viridis', cbar_kws={'label': 'pseudo-log(population density / km²)'})
    axes[2].set_title('pseudo-log transformation')
    
    plt.tight_layout()
    plt.show()


plot_heatmaps(data)

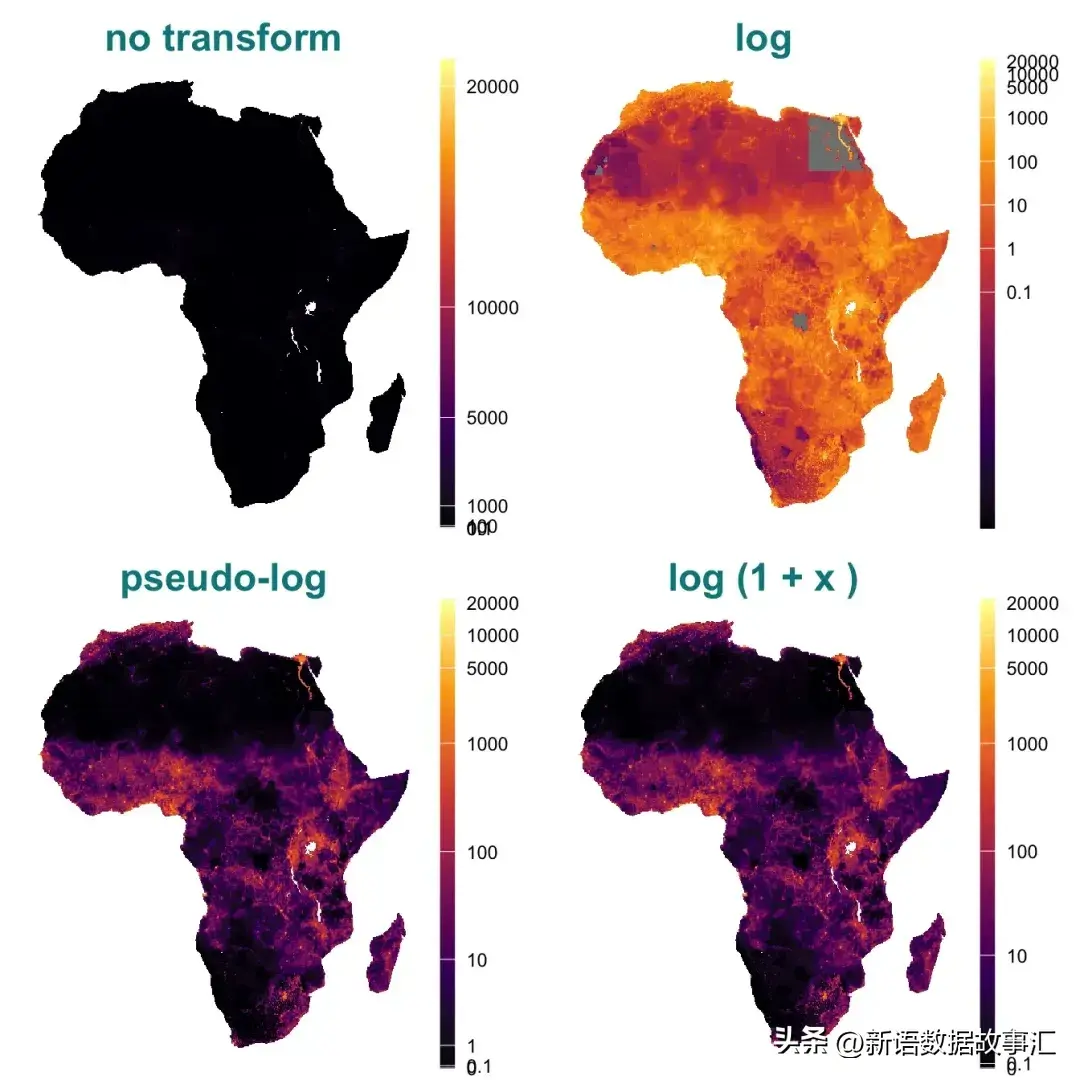
下图是https://www.databrewer.co/blog/pseudo-log-transformation 上面的R语言生成的示例图：

偏斜数据是分布不均的数据，对可视化，特别是热力图绘制提出了挑战。经典对数变换不能处理零和负数，而伪对数变换可以应对这一问题。伪对数在所有实数上都有定义，并能平滑过渡。本文通过比较伪对数和经典对数变换，展示了伪对数在处理和可视化偏斜数据中的优越性。通过实例数据，显示伪对数变换能够有效地改善数据分布和可视化效果，使得数据展示更加清晰。