Go与神经网络：线性回归

离发表上一篇与机器学习相关的文章《Go与神经网络：张量运算》[1]已经过去整整一年了，AI领域，特别是大模型领域的热度不仅未有减弱，反而愈演愈烈。整个行业变得更卷，竞争更加激烈，大模型你方唱罢我登场，层出不穷，各自能力也都在不断提升，并在自然语言处理、问答、生成等方面展现出强大的能力。同时基于RAG(Retrieval-Augmented Generation)[2]等技术，大模型还可以实时检索相关知识并融合到生成结果中，进一步提升了大模型在专业领域的应用价值。

很多人说用好大模型不必非要了解大模型的底层原理，也许这句话是对的。但对于后端程序员的我来说，对底层原理的不理解，始终让我有一种“不安全感”。我认为即使大模型的使用变得日益简单和广泛，但如果我们无法深入理解其工作机制，恐怕还是难以充分发挥它们的潜力，甚至无法准确评估它们的局限性和风险。

但对大模型原理的学习是一个循序渐进的学习过程，我们不能一蹴而就地达到对大模型原理的深入理解。我决定从最基础的机器学习入手，从传统机器学习解决问题的一般步骤开始，以线性回归这个传统传统机器学习的"Hello, World"示例为切入点，逐步探讨机器学习的基本概念和实现流程，这也是本篇文章的初衷与主要内容。

1. 机器学习的那些事儿

1.1 人工智能的诞生

相对于机器学习（Machine Learning，ML），普通大众更熟悉“人工智能（Artificial Intelligence，AI）[3]”这个字眼儿。

就像一千个人眼中有一千个哈姆雷特，每个人对人工智能的理解都不尽相同：有些人将其看成一个学术领域，有些人视之为人类文明下一个要实现的目标，懵懂无知的少年会将其想象为那种高大威猛的机器人（其实是隶属于具身智能[4]，人工智能和机器人学[5]的一个跨学科分支），而还有些人认为它是空中楼阁，永远无法实现。

作为程序员，我们更聚焦工程领域。而工程领域主要是消化学术领域的研究，将其实现落地并应用于人类生活的方方面面。那么学术领域是如何定义人工智能的呢？人工智能专家Stuart Russell[6]和Peter Norvig[7]在他们的联合著作《人工智能：现代方法（第4版）》中将人工智能定义为对从环境中接收感知并执行动作的智能体(Agent)的研究，并强调每个这样的智能体都要实现一个将感知序列映射为动作的函数。

对人工智能的定义虽然内容不长，但这里面却蕴含着计算机科学家对人工智能几十年的探索历程与尝试。

人工智能的概念始于20世纪50年代。1950年，阿兰·图灵（Alan Turing）[8]发表了《计算机器与智能[9]》一文，提出了著名的图灵测试[10]。但人工智能一词的正式提出还要等到6年后的1956年达特茅斯会议。对于人工智能领域而言，这是堪比理论物理学界1927年比利时第五届索尔维会议（如下图）[11]的一次会议。约翰·麦卡锡（John McCarthy）、马文·闵斯基（Marvin Minsky，人工智能与认知学专家）、克劳德·香农（Claude Shannon，信息论的创始人）、艾伦·纽厄尔（Allen Newell，计算机科学家）、赫伯特·西蒙（Herbert Simon，诺贝尔经济学奖得主）等科学家正聚在一起，讨论着一个完全不食人间烟火的主题：用机器来模仿人类学习以及其他方面的智能。会议足足开了两个月的时间，虽然大家没有达成普遍的共识，但是却为会议讨论的内容起了一个名字：人工智能。因此，1956年也就成为了人工智能元年。

1927年比利时第五届索尔维会议合影

1.2 符号主义：早期的人工智能实现路径

在人工智能的早期探索阶段，研究主要集中于符号主义（Symbolism）和逻辑推理。这种方法使用符号来表示知识和问题，并通过逻辑推理来解决问题。这种方法依赖于明确的规则和符号系统来进行推理和决策。

逻辑推理是符号主义的核心，它使用逻辑规则来进行推理和决策。逻辑推理包括演绎推理、归纳推理和溯因推理：

• 演绎推理：从一般规则推导出特定结论（例如，从“所有人都会死”推导出“苏格拉底会死”）。
• 归纳推理：从特定实例推导出一般规则（例如，从“苏格拉底会死”推导出“所有人都会死”）。
• 溯因推理：从结果推断出可能的原因（例如，从“苏格拉底死了”推断出“他是人”）。

LISP语言[12]在符号主义和逻辑推理盛行的阶段发挥了重要作用，其强大的符号处理能力、递归和动态特性、交互式开发环境以及宏和元编程功能使其成为AI研究和开发的主要工具。其他语言如Prolog和Scheme也在特定领域中提供了重要支持。

虽然在机器学习大行其道的今天，符号主义系统不受待见了，但不可否认符号主义系统也有很多优点：

• 可解释性：符号主义系统的推理过程透明、易于理解。
• 明确规则：使用明确的规则和逻辑，使得系统行为可预测。
• 可靠性：在明确定义的领域内，符号主义系统可以提供可靠的推理结果。

不过，它的缺点也很明显：

• 局限性： 依赖于预定义的规则和知识库，难以处理复杂和动态的环境。
• 知识获取： 知识工程需要大量人工干预，获取和维护知识库成本高。

正是由于这些这些不足，以及当时计算能力和数据存储的限制，AI研究在1970年代遇到了障碍，进入了第一次“AI寒冬”。许多早期的承诺未能实现，资金和兴趣减少。

1980年代，符号主义和逻辑推理迎来了第二次巅峰：知识工程和专家系统。专家系统是计算机程序，旨在模仿人类专家的决策能力。它们在特定领域内使用显式编码的知识库和推理引擎来解决复杂问题或提供建议。第一个成功的商用专家系统R1在数字设备公司(Digital Equipment Corporation，DEC)投入使用(McDermott, 1982)，该程序帮助公司配置新计算机系统的订单。截至1986年，它每年为公司节省约4000万美元。到1988年，DEC的人工智能小组已经部署了40个专家系统，而且还有更多的专家系统在开发中。但事实证明，为复杂领域构建和维护专家系统是困难的，一部分原因是系统使用的推理方法在面临不确定性时会崩溃，另一部分原因是系统无法从经验中学习。专家系统的局限性和开发维护成本直接也导致了第二次“AI寒冬”的到来。

在两次AI的兴起和“寒冬”中，先行研究者们开发了许多基础性的算法和系统。这些早期研究不仅解决了特定问题，还为AI的理论和实践发展奠定了重要的基础。随着计算能力和数据资源的增加，AI研究逐渐从符号主义转向数据驱动的方法，但这些早期成果仍然具有重要的历史和学术意义。

1.3 数据驱动与机器学习

数据驱动方法依赖于大量数据，通过从数据中学习模式和关系来进行预测和决策。这种方法不依赖于明确的布尔逻辑和规则，而是通过统计和算法来从数据中提取知识，即基于机器学习而不是手工编码。

1990年代至2000年代，随着计算能力的提升和数据量的增加，机器学习（ML）逐渐成为AI的主要方法。基于统计学和概率论的算法（如支持向量机和决策树）获得了成功。大数据的可用性和向机器学习的转变帮助人工智能恢复了商业吸引力。大数据是2011年IBM的Watson系统在《危险边缘》(Jeopardy!)问答游戏中战胜人类冠军的关键因素，这一事件深深影响了公众对人工智能的看法。

《人工智能：现代方法（第4版）》是这样定义机器学习的：如果一个智能体通过对世界进行观测来提高它的性能，我们称其为智能体学习(learning)。学习可以是简单的，例如记录一个购物清单，也可以是复杂的，例如爱因斯坦推断关于宇宙的新理论。当智能体是一台计算机时，我们称之为机器学习(machine learning)：一台计算机观测到一些数据，基于这些数据构建一个模型(model)，并将这个模型作为关于世界的一个假设(hypothesis)以及用于求解问题的软件的一部分。不通过合适的方式编程来解决，而是希望一台机器自主进行学习并解决问题，其原因主要有两个：

• 程序的设计者无法预见未来所有可能发生的情形。比如一个被设计用来导航迷宫的机器人无法掌握每一个它可能遇到的新迷宫的布局。
• 有时候设计者并不知道如何设计一个程序来求解目标问题。比如识别人脸。

可以说，机器学习是另外一种实现人工智能的路径（前一种是符号主义和逻辑推理），它是一类强大的可以从经验中学习的技术。通常采用观测数据或与环境交互的形式，机器学习算法会积累更多的经验，其性能也会逐步提高。

机器学习的兴起同样离不开早期研究者的成果：

• 感知机（1957）： Frank Rosenblatt 设计的感知机是第一个用于分类任务的人工神经网络模型，能够学习二分类任务。感知机也被视为一种最简单形式的前馈式人工神经网络。
• K均值聚类（1967）： James MacQueen 提出的K均值聚类算法，是最早的聚类分析方法之一。
• 决策树（ID3, 1986）： Ross Quinlan 提出的 ID3 算法，是决策树学习的基础。
• 支持向量机（1992）： Vladimir Vapnik 和 Alexey Chervonenkis 提出了支持向量机，为高维数据分类问题提供了强有力的解决方案。
• 多层感知器（1986）： 由 Geoffrey Hinton 等人推广的反向传播算法（Backpropagation），使得训练多层神经网络成为可能。
• 梯度提升树（2000）： Jerome Friedman 提出的梯度提升树（Gradient Boosting Machines），在分类和回归任务中表现出色。
• 随机森林（2001）： Leo Breiman 提出的随机森林算法，通过集成多个决策树提高了模型的准确性和鲁棒性。

进入2010年后，在大规模数据集以及GPU硬件加速的赋能下，深度神经网络逐渐成为主流且表现卓越的机器学习方案，深度学习走向前台：

• AlexNet（2012）： Alex Krizhevsky 等人在 ImageNet 大赛上使用卷积神经网络（CNN）赢得了第一名，推动了深度学习在计算机视觉中的应用。
• 生成对抗网络（GAN, 2014）： Ian Goodfellow 等人提出的生成对抗网络，开启了生成模型的新方向。
• BERT（2018）： Google 提出的双向编码器表示（BERT）模型，在自然语言处理任务中取得了突破性进展。
• Transformers（2022）：Transformers模型及其变种在自然语言处理、图像处理等多个领域取得了显著进展，典型代表是ChatGPT的推出。

1.4 人工智能关系图

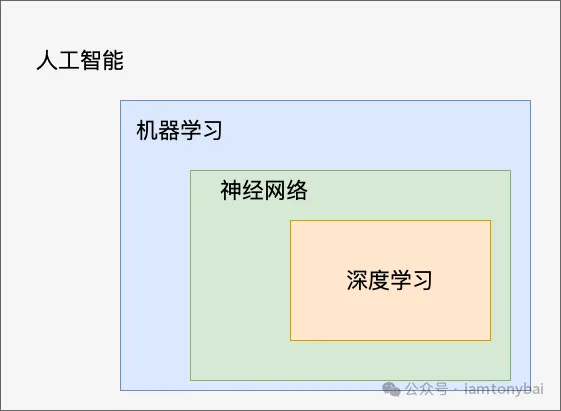
基于上面的说明，我们下面用一张图说明一下人工智能、机器学习、神经网络以及深度学习的关系：

图片

而神经网络是支撑机器学习的重要技术，是深度学习的核心技术。关于神经网络，我们会在后面的系列文章中重点说明。

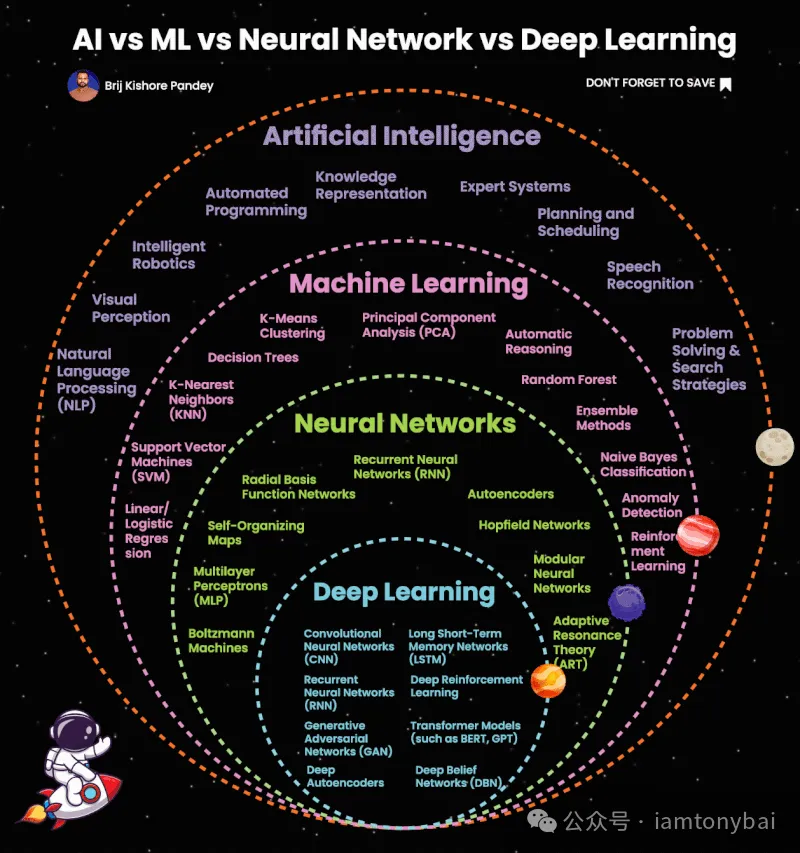
网络上也有一个图，可以更详细地展示各个范围内的具体技术，大家也可以参考一下：

图片

1.5 机器学习的本质

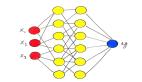
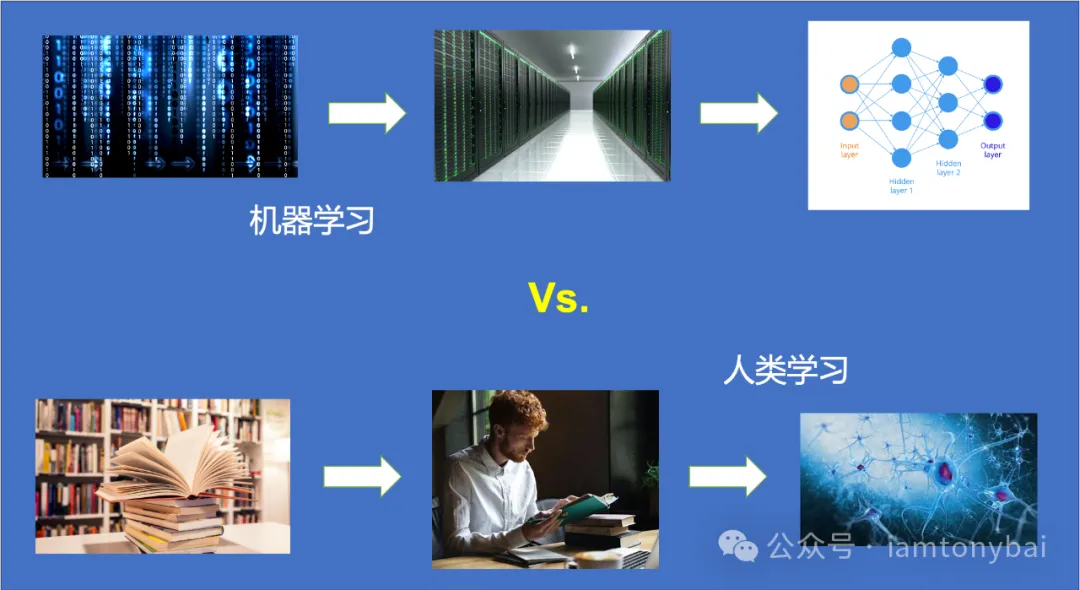
机器学习就是从数据中发现规律，发现的这个规律就是“模型”， 更具体来说就是一个或一组复合在一起的函数。而发现规律的这个过程就叫“学习”或叫“训练”。这个过程与人类学习的有些相似：

图片

人类和机器都需要输入信息来开始学习。人类通过感官感知信息，机器通过传感器或数据集获取数据。人类通过理解和记忆进行学习，机器通过训练数据调整模型参数进行学习。人类在大脑中存储知识和经验，机器在模型参数和结构中存储学到的模式和规则。人类根据实践中的反馈调整和改进知识，机器根据评估和实际应用中的反馈调整模型参数和结构。两者尽管实现手段不同，但核心思想都是从输入数据中学习知识和模式，通过反馈进行调整和改进，并不断适应新的环境和问题。

上图中使用神经网络的形式呈现了学习/训练后的模型，其实在一些传统机器学习的简单场景下，训练后的模型可能就是一个简单的一元线性函数，比如：f(x) = wx + h。

训练后的模型便可以应用于真实环境中的数据，进行推理和预测（serve/predict）。比如说，一个经过大量真实病历数据训练后得到医疗诊断模型，就可以用来预测和诊断新的病患情况了。

到这里，你可能依然对机器学习一知半解。别着急，之前我也是这样，就想亲手训练一个模型来直观体会一下什么是机器学习。接下来，我们就来训练一个Hello，World级别的模型，不过在真正动手之前，我们还是要先来了解一下机器学习中的术语（“黑话”）与训练的一般步骤。

2. 机器学习的术语与一般步骤

机器学习本身就有不低的门槛，因此我们将由浅入深的来学习机器学习的术语，并简要说明一下机器学习项目的一般步骤。

2.1 特征、标签与模型

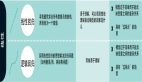
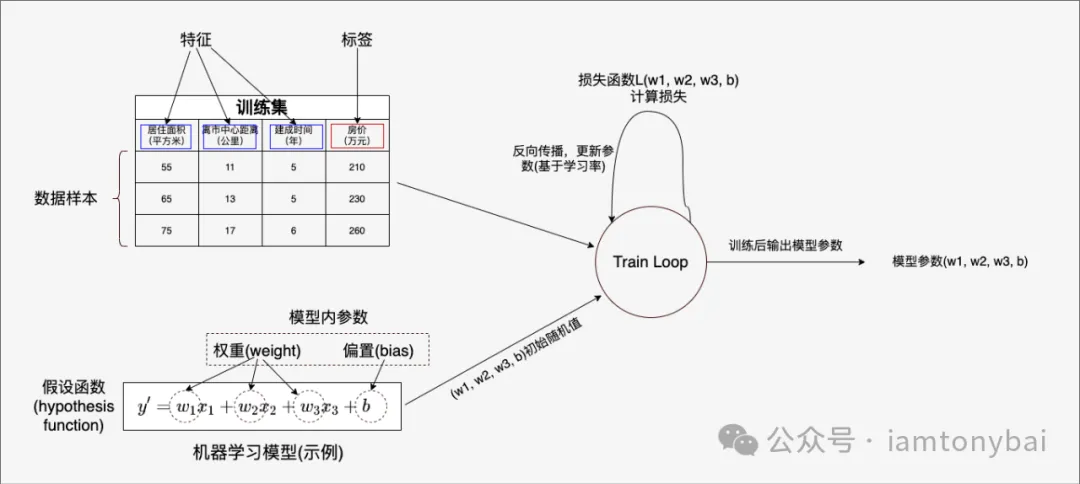
在下图中，我们以一个简单的多元线性回归模型（即一个多元一次函数）来说明一下一些机器学习中常见的术语：

图片

我们先介绍与数据有关的几个重要术语，其他在后面说明机器学习的一般步骤时，结合具体的场景再行讲解。机器学习离不开数据，如上图中左上角的表格就是“喂给”机器学习训练的**训练数据集(training dataset )**。

上图中的数据集是一个常见的房价相关数据，该数据集有三条数据，它们组成了该数据集的数据样本。表中每条数据有三个影响房价的“因子”：居住面积、离市中心距离和建成时间（也就是房龄），这些因子共同决定了房子的价格。在机器学习中，我们称这些“因子”为**特征(feature)。而房价则被称为标签(label)**。从数据来看，这三个特征表现出明显的与房价(y)的相关性，如下图：

图片

机器学习的目的就是找到通过特征预测标签的函数（即模型），然后将得到的函数应用于生产中进行标签预测。特征是机器学习模型的输入，标签是机器学习模型的输出。无论是在训练阶段，还是在预测阶段。特征的个数称为特征的维度，维度越高，数据集越复杂。

了解完特征、标签和模型后，我们来看看机器学习项目的一般步骤，更具体来说就是机器学习训练的步骤，一旦训练ok，得到模型，模型应用就比较简单了。

2.2 机器学习训练的一般步骤

图片

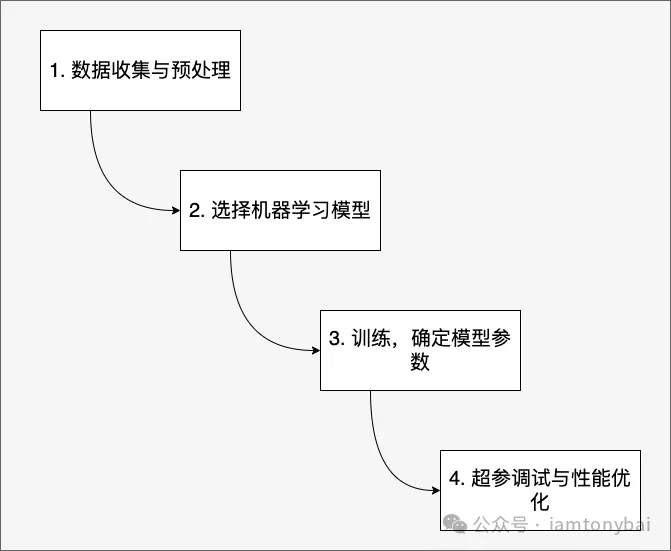
上图展示了机器学习训练的一般步骤，我们逐个说明一下。

2.2.1 数据收集与预处理

就像人类要从各种资料（书籍、媒体等)中学习一样，机器也要从数据中学习。没有数据，机器学习就无从谈起。数据也是通过机器学习解决生活中实际问题的前提。

数据收集渠道有多种，有爬取互联网的数据，有开源数据集（Image Net、Kaggle、Google Public Data Explorer），有购买的，还有客户积攒的海量历史数据等。这些数据拿到手后，还不能直接喂给模型进行训练，因为业界有句名言“输入的是垃圾，输出的也是垃圾”(Garbage in, garbage out)，我们需要对数据进行分析和预处理，了解数据内在关系并使其满足机器学习训练的规格和质量要求，最后还需要做特征的提取，即使用数据的领域知识来创建/识别出那些使机器学习算法起作用的特征的过程。

数据的预处理是十分重要的工作，预处理的好坏直接决定了训练出来的机器学习模型的有效性。在《零基础学习机器学习》一书中提到了数据预处理工作包含的几项内容：

• 可视化：用Excel表和各种数据分析工具(如Matplotlib等)从各种角度(如列表、直方图、散点图等)探索一下数据。对数据有了基本的了解后，才方便进一步分析判断，即为后续的模型选择奠定基础。
• 数据向量化[13]：把原始数据格式化，使其变得机器可以读取。例如，将原始图片转换为机器可以读取的数字矩阵，将文字转换为one-hot编码，将文本类别(如男、女)转换成0、1这样的数值。
• 处理坏数据和空数据：一条数据可不是全部都能用，要利用数据处理工具来把“捣乱”的“坏数据”(冗余数据、离群数据、错误数据)处理掉，把缺失值补充上。
• 特征缩放：可以显著提升模型的性能和训练效率。许多机器学习算法，例如梯度下降法，依赖于特征之间的距离计算。如果特征的尺度差异很大，会导致算法在不同特征方向上以不同的速度进行更新，从而降低收敛速度。特征缩放可以将所有特征缩放到相同的尺度，使算法能够更快地收敛到最优解。特征尺度差异过大可能导致数值计算不稳定，例如出现梯度爆炸或梯度消失现象，影响模型训练效果。特征缩放还可以使模型的权重更加可解释。当特征尺度差异很大时，模型的权重可能无法反映特征的实际重要性。特征缩放可以使权重更加反映特征的真实贡献。

特征缩放适用于大多数机器学习算法，包括线性回归、逻辑回归、支持向量机、神经网络等。常见的特征缩放方法包括如下几种：

• 标准化 (Standardization)：对数据特征分布的转换，目标是使其符合正态分布(均值为0，标准差为1)。在实践中，会去除特征的均值来转换数据， 使其居中，然后除以特征的标准差来对其进行缩放。
• 归一化/规范化 (Normalization)：将特征数据缩放到特定范围，通常是0到1之间。归一化不会改变数据的分布形态。

数据预处理还包括特征工程和特征提取，即确定数据中究竟哪个特征对问题的解决会起到关键作用，并提取出来作为后续训练和预测的输入特征。许多现代机器学习算法，如深度学习模型，可以从原始数据中学习复杂的表示形式，而不需要明确的特征工程，但是特征工程仍然在机器学习工作流程中扮演着重要角色，尤其是在领域知识、可解释性和数据质量方面起到重要作用。不过特征提取是一个细分领域，内容很多(对之我也不甚了解)，这里就不展开说了。

2.2.2 选择机器学习模型

AI科学家期望能有一个通用的机器学习模型可以学习一切类型的数据，并处理所有领域的任务，这样世界将变得简单了。但就目前AI发展的水平来看，还没有一个通用的机器学习模型可以适合于所有类型的数据和任务，即便是当今大热的预训练的大语言模型也可能不胜任某一领域的工作。在前期的传统机器学习阶段，不同的数据和问题需要采用不同的机器学习方法和模型。

影响机器学习模型选择的一些关键的因素包括：

• 数据类型和特征：比如图像数据和文本数据一般需要不同的模型。数据的维度、稀疏程度等也会影响选择的模型。
• 任务类型：分类、回归、聚类等任务适合不同的模型。有监督学习和无监督学习也需要不同的方法。
• 数据规模：对于大规模数据，可扩展性强的模型如深度学习效果更好。小样本数据可能更适合传统的机器学习算法。
• 领域知识：某些领域问题需要结合专业领域知识，不能单纯依赖通用的机器学习模型。

这里提到了有监督学习和无监督学习，提到了分类、回归、聚类等任务类型，我们需要简单科普一下这些概念。

机器学习中，有监督学习和无监督学习是两种主要的学习方法，它们有各自擅长的任务类型。

有监督学习是一种通过使用已标注的数据(即如前面图中的训练数据集那样，样本数据包含特征与对应的标签)来训练模型的方法。在这种方法中，每个训练样本都是一个输入-输出对，模型通过学习这些对的关系来预测新的输入数据的输出。有监督学习擅长的任务类型包括下面这几个：

• 分类任务：将输入数据分类到预定义的类别中，例如垃圾邮件检测、图像分类。
• 回归任务：预测连续的数值输出，例如房价预测（前面图中的示例）、股票价格预测。
• 标注任务：为输入数据中的每个元素分配一个标签。例如：命名实体识别（NER）：在文本中识别出人名、地名、组织名等。
• 排序任务：根据某种标准对项目进行排序。例如：信息检索、推荐系统。
• 序列预测任务：根据时间序列数据进行预测。例如，销售额预测、天气预报等。

使用有监督学习，我们需要向模型提供巨大数据集，且每个数据样本都需要包含特征和相应标签值，这很可能是一个既耗时又费钱的过程。

而无监督学习则是一种通过使用未标注的数据来训练模型的方法。在这种方法中，模型试图从数据中发现结构或模式，而无需使用明确的输入-输出对。无监督学习擅长的任务类型包括下面几个：

• 聚类任务：将相似的样本归为一类，比如给定一组照片，模型能把它们分成风景照片、狗、婴儿、猫和山峰。同样，给定一组用户的网页浏览记录，模型能将具有相似行为的用户聚类。
• 降维任务：减少数据的维度，同时保持其重要特征，例如主成分分析（PCA）问题，模型能否找到少量的参数来准确地捕捉数据的线性相关属性？比如，一个球的运动轨迹可以用球的速度、直径和质量来描述。
• 异常检测：识别数据中的异常或异常模式，例如欺诈检测、设备故障检测。

这两种方法在不同的应用场景中各有所长，选择哪种方法通常取决于数据的特性和具体的任务需求。

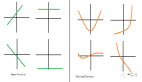
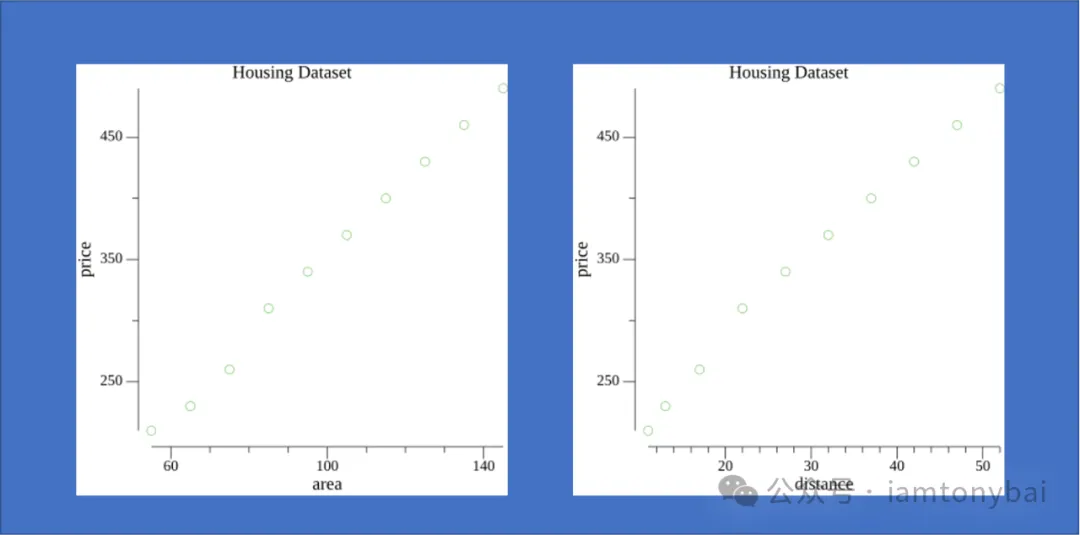
我们以前面图中的房价预测问题为例，根据前面关于有监督和无监督的任务类型以及带有标签的数据对的训练数据集，我们初步判断应该选择线性回归模型。当然，你也可以自己探索数据集中一些特征与标签的关系，比如我们利用gonum.org/v1/plot相关包分别画出房屋面积、离市中心距离两个特征与标签房价的散点图（当然这是自己生成的一组训练数据集，具体描画代码参见https://github.com/bigwhite/experiments/blob/master/go-and-nn/linear-regression/plotter.go）：

图片

从数据的特征散点图，可以看出一些特征与标签之间的线性关系，这符合使用线性回归模型的要求。线性回归基于几个简单的假设：首先，假设自变量(x1, x2, x3, ..., xn)和因变量y之间的关系是线性的，即y可以表示为自变量集合中元素的加权和。以前面的房价预测问题为例，线性模型对应的假设函数可以表示为居住面积、与市中心距离以及房龄的加权和，就像下面这样：

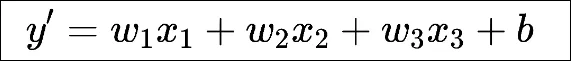图片

这个函数叫做假设函数（也叫预测函数），其中的w1、w2和w3称为权重，权重决定了每个特征对我们预测值的影响。b称为偏置(bias)、 偏移量(offset)或截距(intercept)。偏置是指当所有特征都取值为0时，预测值应该为多少。

现在权重w1、w2、w3和偏置b的值都是未知的，它们也被称为模型内的参数，直接影响模型的预测结果。

接下来的训练就是为了得到这些参数的合理值，使得假设函数得到的结果与真实房价越接近越好。

2.2.3 训练

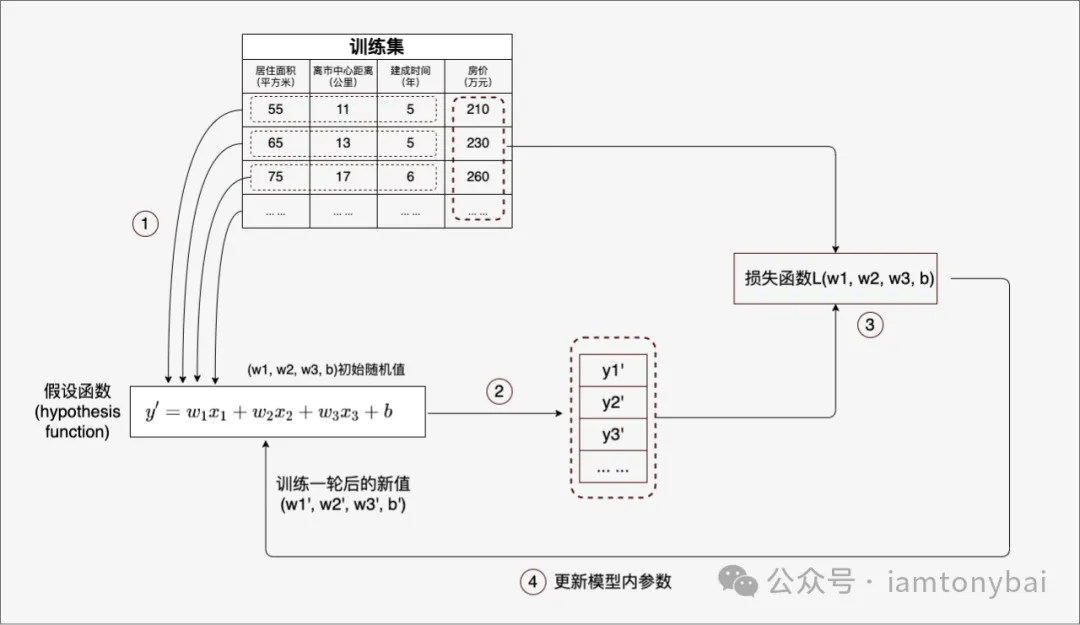
到这里，我们拥有了一份训练数据集（带标签）以及一个权重和偏置参数未知的多元线性假设函数（y'）。而我们接下来要做的就是找到假设函数中各个未知参数的合理值。

图片

机器学习的“学习训练”过程非常朴素，就是将训练数据集中的特征逐条喂给y'，并将得到的结果与训练数据集中的标签比对，如果差距过大，则调整y'的权重参数和偏置，然后再重复一轮学习，这样循环往复直到通过y'计算得到的结果与标签的差距在预期范围以内。

不过，这个过程看似容易，但真正实施起来，还有很多“阻塞点”要突破。以y'这个多元线性函数模型为例，首先就是权重和偏置参数的初始值。在我们这篇入门文章中，针对y'这个简单的线性函数，我们可采用随机初始化的方式，即将参数随机地设置在一个合理的范围内。这种方法简单快捷，但对于复杂的模型，可能会导致收敛速度慢或陷入局部最优。关于初始参数的选择也是一个细分方向，这里就不展开说明了。

其次，我们要确定一个y'计算结果与训练数据集中标签值的差距计算方法。机器学习领域称这个计算方法为损失函数(Loss function)。损失也就是 误差，也称为成本(cost)或代价，用于体现当前预测值和真实值之间的差距。它是一个数值，表示对于单个样本而言模型预测的准确程度。如果模型的预测完全准确，则损失为0；如果不准确，就有损失。在机器学习中，我们追求的当然是比较小的损失。不过，模型好不好还不能仅看单个样本，而是要针对所有数据样本，找到一组平均损失“较小”的函数模型。计算平均损失是每一个机器学习项目的必要环节。损失函数实质上就是用来计算平均损失的，它是模型参数的函数：L(w1, w2, w3, b)。机器学习的训练过程就是找一组模型参数的解，比如本示例中的（w1, w2, w3, b），使得损失函数的计算结果最小。

机器学习中的损失函数有很多，针对不同任务类别，选择一个合适的即可。

比如，用于回归的损失函数就有：均方误差(Mean Square Error，MSE)函数、平均绝对误差(Mean Absolute Error，MAE)函数和平均偏差误差(mean bias error)函数。用于分类的损失函数有交叉熵损失(cross-entropy loss)函数和多分类SVM损失(hinge loss)函数等。

对于我们的回归问题来说，下面的均方差函数L就可以满足评估参数的目的了。

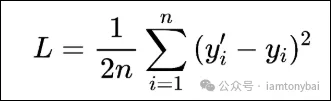图片

在这个函数中，yi'基于样本数据的特征经由假设函数计算出来的值，yi则是样本数据的标签值。假设只有一个样本数据如下：

x1 = 55, x2 = 11, x3 = 5, y = 210

我们的假设函数为：y' = 0.1x1 + 0.1x2+0.1x3 + 0.1 ，即初始参数w1 = w2 = w3 = b = 0.1。那么我们可以计算一下针对这个样本的损失：

y' = 0.1 * 55 + 0.1 * 11 + 0.1 * 5 + 0.1 = 7.2
L = 1/2 * (7.2 - 210)^2 = 20563.920000000002

这个损失函数值看起来就不大行:)，我们需要调整模型参数再战！但如何调整呢？w1调大？w2调小？w3不动？尽管现在算力已经很强大了，但我们也不能拍脑袋乱猜！我们需要一种科学的方法为机器学习后续的参数调整指明方向，这样才能大幅缩短训练过程，并得到满足需求的模型参数组合。

大多流行的优化算法通常基于一种基本方法–梯度下降(gradient descent)。简而言之，在每个步骤中，梯度下降法都会检查每个参数，看看如果仅对该参数进行少量变动，训练集损失会朝哪个方向移动。然后，它在可以减少损失的方向上优化参数。

梯度下降的过程就是在程序中一点点变化参数w1、w2、w3和b，使L ，也就是损失值逐渐趋近最低点(也称为机器学习中的最优解)。而要实现这一点，我们需要借助导数。导数描述了函数在某点附近的变化率(比如：L正在随着w1增大而增大还是减小)，而这正是进一步猜测更好的权重时所需要的全部内容。即梯度下降法通过求导来计算损失曲线在起点处的梯度。此时，梯度就是损失曲线导数的矢量，它可以让我们了解哪个方向距离目标“更近”或“更远”。如果求导后梯度为正值，则说明L正在随着w增大而增大，应该减小w，以得到更小的损失。如果求导后梯度为负值，则说明L正在随着w增大而减小，应该增大w，以得到更小的损失。

在单个权重参数的情况下，损失相对于权重的梯度就称为导数；若考虑偏置，或存在多个权重参数时（就像我们上面的房价预测示例），损失相对于单个权重的梯度就称为偏导数。

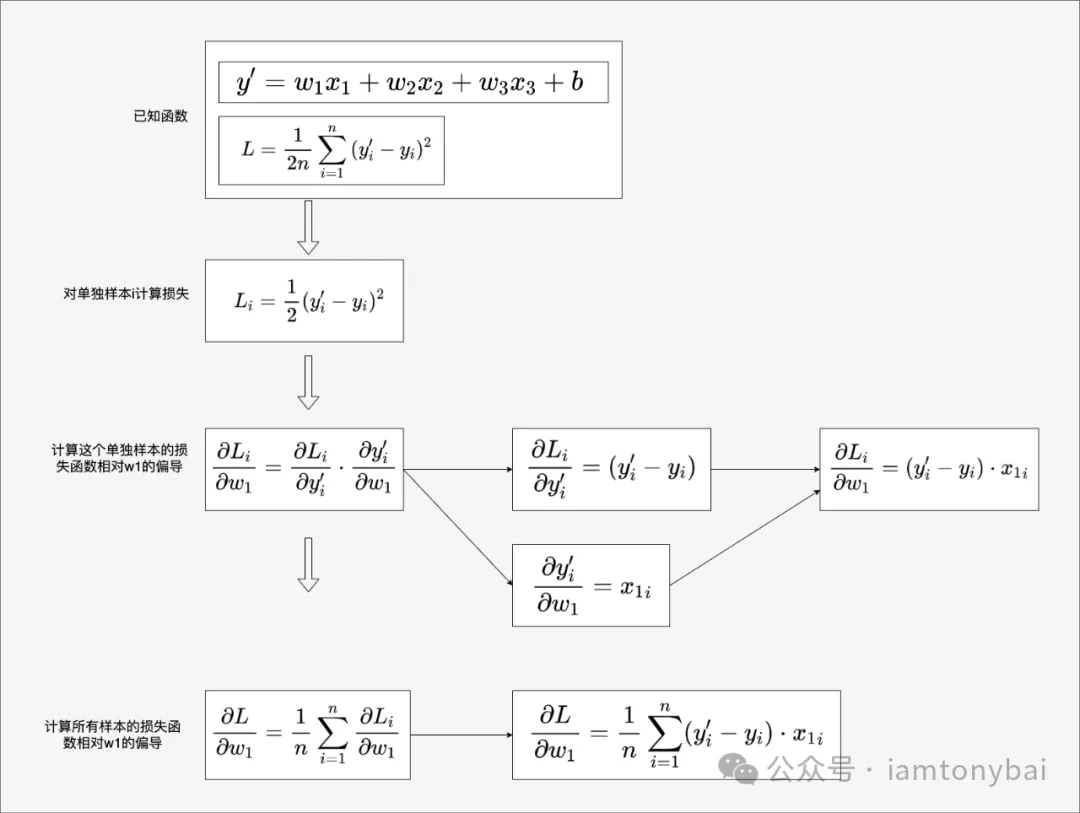
在上面示例中，损失函数L是权重参数和偏置的函数，表示为L(w1, w2, w3, b)。我们需要分别求出L相对于w1、w2、w3和b的偏导数来决定后续各个权重参数和偏置参数的调整方向（增大还是减小）。我们以L对w1的偏导数为例，给出偏导数公式的推导过程：

图片

我们看到：针对每个样本，我们计算其损失值(y'-y)与该样本特征(x1)的乘积。取这些乘积的平均值就得到了L对w1的偏导值。

依次类推，我们可以得到L对w1、w2、w3和b的偏导数公式：

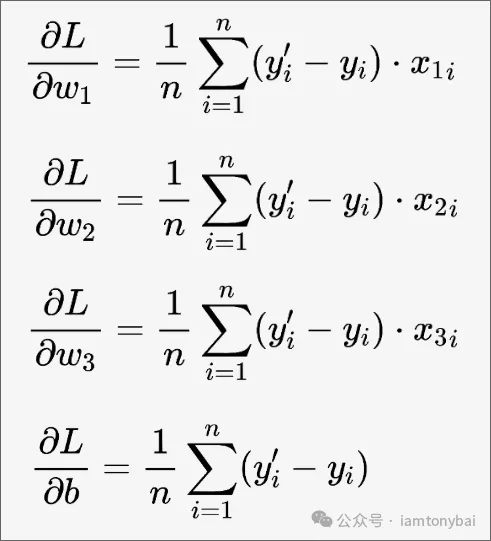图片

上面的偏导数为我们指定了参数调整方向，下面是w1、w2、w3和b的更新公式：

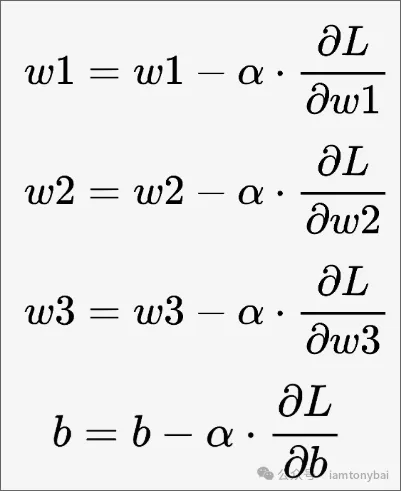图片

这种计算梯度并反向更新模型参数的过程就称为“反向传播”。

上面参数更新公式中有一个新的变量α，该变量代表的是学习率(learning rate)。是一个超参数，它控制着模型参数更新的步伐大小。在梯度下降过程中，学习率决定了每次更新参数时移动的步长。学习率的引入是为了控制模型训练的速度。如果学习率太大，参数更新步伐过大，可能导致模型无法收敛甚至发散；如果学习率太小，参数更新步伐过小，训练时间会过长且可能陷入局部最小值。

w1的更新公式是w1减去损失函数相对于w1的偏导数乘以学习率，这个公式表示，我们沿着损失函数梯度的负方向更新参数，因为梯度的方向是损失函数增大的方向，所以负方向是使损失函数减小的方向。

到这里，我们已经可以实现训练的闭环了！训练后的模型可以使用另外一套测试数据集来评估模型的效果。但训练出来的模型是否真的是满足要求的呢？还不一定，很多情况下，我们还需要对超参进行调试以继续优化模型。

2.2.4 超参调试与性能优化

在上面的讲解中，我们知道w1、w2、w3和b是模型内的参数，这些参数通过y'正向传播和基于梯度下降的反向传播在多轮训练中得以更新优化，并得到一个合理的值。这些值是机器从数据中学习到的，不需要我们手工调整。但还有一些参数，比如上面提到的学习率(learning rate)、训练轮数(Epochs)等，是模型外部的可以通过人工调节的参数，这样的参数称为**超参数(Hyperparameters)**。大多数机器学习从业者真正花费相当多的时间来调试的正是这类超参数。

在实际应用中，选择合适的学习率和训练轮数等超参数通常需要结合以下方法：

• 经验法则：基于先前经验和领域知识设定初始值。
• 交叉验证：通过交叉验证选择一组最优的超参数。
• 网格搜索：在多个可能的超参数组合上进行搜索，找到效果最好的参数组合。
• 学习率调度：动态调整学习率，比如在训练过程中逐渐减小学习率。

超参数对模型效果和优化的影响非常重要，选择合适的超参数可以显著提高模型性能。本文是入门文章，关于超参的调优就不展开说明了。

基于通过上面的对机器学习的术语、概念和对训练一般步骤的了解，接下来，我们通过一个实例来训练一个最简单的机器学习模型：线性回归模型。这也被称为机器学习领域的“Hello, World”。

3. 线性回归：机器学习的Hello, World

我们按照前面关于机器学习的一般步骤，逐步展开该示例的说明。

3.1 准备数据和预处理

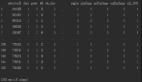
我们这个示例依旧是预测房价，但是为了简单，我们不使用那些公共数据集（比如kaggle平台[14]上的数据），而是让大模型帮我生成两个小规模的数据集，一个是用于训练的train.csv，一个是用于测试的test.csv：

$cat train.csv
面积,距离,房价
50,10,200
60,12,220
70,15,250
80,20,300
90,25,330
100,30,360
110,35,390
120,40,420
130,45,450
140,50,480

$cat test.csv 
面积,距离,房价
55,11,210
65,13,230
75,17,260
85,22,310
95,27,340
105,32,370
115,37,400
125,42,430
135,47,460
145,52,490

还是为了简单，我们在这两份数据集中仅使用两个特征：面积和离市中心距离。

接下来，我们就通过编码来实现对csv文件的读取：

// go-and-nn/linear-regression/main.go
func readCSV(filePath string) ([][]float64, error) {
    file, err := os.Open(filePath)
    if err != nil {
        return nil, err
    }
    defer file.Close()

    reader := csv.NewReader(file)
    records, err := reader.ReadAll()
    if err != nil {
        return nil, err
    }

    data := make([][]float64, len(records)-1)
    for i := 1; i < len(records); i++ {
        data[i-1] = make([]float64, len(records[i]))
        for j := range records[i] {
            data[i-1][j], err = strconv.ParseFloat(records[i][j], 64)
            if err != nil {
                return nil, err
            }
        }
    }
    return data, nil
}

readCSV用于从CSV文件中读取所有样本数据（已去掉了header），所有样本数据（包括特征与标签）都存储在一个[][]float64类型的变量中。

拿到数据后，我们便可以对其进行标准化，前面说过通常情况下，标准化后的数据会使模型训练更加稳定和快速，从而可能提高模型的预测性能。下面是我们实现用于对训练数据集进行标准化的函数：

// go-and-nn/linear-regression/main.go
func standardize(data [][]float64) ([][]float64, []float64, []float64) {
    mean := make([]float64, len(data[0])-1)
    std := make([]float64, len(data[0])-1)
    for i := 0; i < len(data[0])-1; i++ {
        for j := 0; j < len(data); j++ {
            mean[i] += data[j][i]
        }
        mean[i] /= float64(len(data))
    }
    for i := 0; i < len(data[0])-1; i++ {
        for j := 0; j < len(data); j++ {
            std[i] += math.Pow(data[j][i]-mean[i], 2)
        }
        std[i] = math.Sqrt(std[i] / float64(len(data)))
    }
    standardizedData := make([][]float64, len(data))
    for i := 0; i < len(data); i++ {
        standardizedData[i] = make([]float64, len(data[i]))
        for j := 0; j < len(data[i])-1; j++ {
            standardizedData[i][j] = (data[i][j] - mean[j]) / std[j]
        }
        standardizedData[i][len(data[i])-1] = data[i][len(data[i])-1]
    }
    return standardizedData, mean, std
}

standardize中的mean和std分别用于存储每个特征的均值和标准差（标准差是反应一组数据离散程度最常用的一种量化形式，累加每个样本的特征值与均值的平方差，然后除以样本数量，再开平方，便可得到该特征的标准差）。有了均值和标准差后，我们用原始特征值减去均值，然后除以标准差，得到标准化后的特征值。标签无需标准化。

3.2 选择机器学习模型

基于前面的铺垫，我们早就明确了适合房屋价格预测的机器学习模型，那就是一个多元线性函数，确定假设函数为：

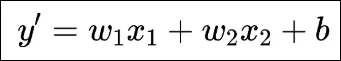图片

损失函数我们也用均方误差(Mean Square Error，MSE)函数，这样损失函数就是w1、w2和b的函数：L(w1, w2, b)。依据前面的介绍，我们可以推导出损失函数L对w1、w2和b的偏导数以及权重更新公式如下：

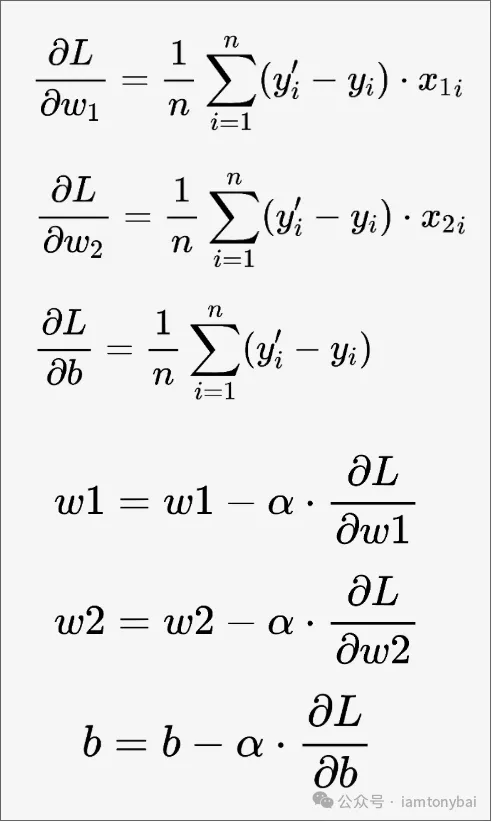图片

确定了模型相关的公式后，我们就可以来实现该模型的训练了！

3.3 训练

下面是训练函数的实现代码：

// go-and-nn/linear-regression/main.go
func trainModel(data [][]float64, learningRate float64, epochs int) ([]float64, float64) {
    features := len(data[0]) - 1
    weights := make([]float64, features)
    bias := 0.0
    
    for epoch := 0; epoch < epochs; epoch++ {
        gradW := make([]float64, features)
        gradB := 0.0
        mse := 0.0
        for i := 0; i < len(data); i++ {
            prediction := bias
            for j := 0; j < features; j++ {
                prediction += weights[j] * data[i][j]
            }   
            error := prediction - data[i][features]
            mse += error * error
            for j := 0; j < features; j++ {
                gradW[j] += error * data[i][j]
            }   
            gradB += error
        }   
        mse /= float64(len(data))
        
  // 更新权重
        for j := 0; j < features; j++ {
            gradW[j] /= float64(len(data))
            weights[j] -= learningRate * gradW[j]
        }   

        gradB /= float64(len(data))
  // 更新偏置
        bias -= learningRate * gradB
        
        // Output the current weights, bias and loss
        fmt.Printf("Epoch %d: Weights: %v, Bias: %f, MSE: %f\n", epoch+1, weights, bias, mse)
    }   
    return weights, bias
}

在这个代码实现中，我们将权重和偏置的初始值都设置为了0，然后进入训练循环，循环的次数由外部传入的epochs来决定，前面提到过epochs也是一个超参。每次循环代表一次完整的训练过程。gradW用于存储每个特征的梯度，gradB则用于存储偏置的梯度值。梯度计算以及后面的更新权重的算法也都是按照上面图片中的公式进行的。注意代码中的error变量并非代表错误，而是表示预测误差（即预测值减去真实标签值）。

下面是驱动训练函数的代码：

// go-and-nn/linear-regression/main.go
func main() {
    // Read training data
    trainData, err := readCSV("train.csv")
    if err != nil {
        log.Fatalf("failed to read training data: %v", err)
    }

    // Read testing data
    testData, err := readCSV("test.csv")
    if err != nil {
        log.Fatalf("failed to read testing data: %v", err)
    }

    // Standardize training data
    standardizedTrainData, mean, std := standardize(trainData)

    // Train model
    learningRate := 0.0001
    epochs := 1000
    weights, bias := trainModel(standardizedTrainData, learningRate, epochs)
    fmt.Printf("Trained Weights: %v\n", weights)
    fmt.Printf("Trained Bias: %f\n", bias)

    // Evaluate model on test data
    predictAndEvaluate2(testData, weights, bias, mean, std)
}

这里我们设置超参学习率为0.0001，设置epochs为1000，即进行1000轮完整的训练。trainModel训练完成后返回最优的权重值和偏置值。

之后，我们基于训练后的模型以及测试数据集进行模型效果评估，

// go-and-nn/linear-regression/main.go
func predictAndEvaluate(data [][]float64, weights []float64, bias float64, mean []float64, std []float64) {
    features := len(data[0]) - 1
    mse := 0.0
    for i := 0; i < len(data); i++ {
        // Standardize the input features using the training mean and std
        standardizedFeatures := make([]float64, features)
        for j := 0; j < features; j++ {
            standardizedFeatures[j] = (data[i][j] - mean[j]) / std[j]
        }

        // Calculate the prediction
        prediction := bias
        for j := 0; j < features; j++ {
            prediction += weights[j] * standardizedFeatures[j]
        }

        // Calculate the error and accumulate the MSE
        error := prediction - data[i][features]
        mse += error * error

        // Print the prediction and the actual value
        fmt.Printf("Sample %d: Predicted Value: %f, Actual Value: %f\n", i+1, prediction, data[i][features])
    }

    // Calculate the final MSE
    mse /= float64(len(data))
    fmt.Printf("Mean Squared Error: %f\n", mse)
}

该评估函数会输出测试集中每一组数据的预测值与标签值的对比。

我们运行一下该代码：

$go build
$./demo
Epoch 1: Weights: [0.009191300234460844 0.009159461537409297], Bias: 0.034000, MSE: 124080.000000
Epoch 2: Weights: [0.018380768863390594 0.01831709148135162], Bias: 0.067997, MSE: 124053.513977
Epoch 3: Weights: [0.02756840625241513 0.027472890197452842], Bias: 0.101990, MSE: 124027.033923
Epoch 4: Weights: [0.03675421276708735 0.036626858051265865], Bias: 0.135980, MSE: 124000.559834
Epoch 5: Weights: [0.04593818877288719 0.0457789954082706], Bias: 0.169966, MSE: 123974.091710
... ...
Epoch 997: Weights: [8.311660331200889 8.279923139396109], Bias: 32.264505, MSE: 100432.407457
Epoch 998: Weights: [8.319195610465172 8.287426591989], Bias: 32.295278, MSE: 100411.202067
Epoch 999: Weights: [8.326729388699432 8.294928543563927], Bias: 32.326049, MSE: 100390.001368
Epoch 1000: Weights: [8.334261666203304 8.302428994420524], Bias: 32.356816, MSE: 100368.805359
Trained Weights: [8.334261666203304 8.302428994420524]
Trained Bias: 32.356816
Sample 1: Predicted Value: 10.081607, Actual Value: 210.000000
Sample 2: Predicted Value: 14.223776, Actual Value: 230.000000
Sample 3: Predicted Value: 19.606495, Actual Value: 260.000000
Sample 4: Predicted Value: 25.609490, Actual Value: 310.000000
Sample 5: Predicted Value: 31.612486, Actual Value: 340.000000
Sample 6: Predicted Value: 37.615481, Actual Value: 370.000000
Sample 7: Predicted Value: 43.618476, Actual Value: 400.000000
Sample 8: Predicted Value: 49.621471, Actual Value: 430.000000
Sample 9: Predicted Value: 55.624466, Actual Value: 460.000000
Sample 10: Predicted Value: 61.627461, Actual Value: 490.000000
Mean Squared Error: 104949.429046

从最终的预测结果输出来看，这个模型的效果那是相当的差！预测值与测试集中的真实标签值相距“十万八千里”！问题出在哪里了呢？我们接下来来看看超参对模型训练的作用。

3.4 超参调试和优化

我们在上面例子中使用的学习率(learningRate)为0.0001，这个数值似乎有些小。

如果学习率太小，模型的更新幅度会很小，导致训练过程非常缓慢，可能需要大量的训练轮次才能收敛。我们这里设置的训练轮次(epochs)为1000，在0.0001如此小的学习率下面，模型可能尚未收敛，训练就结束了！所以，我们尝试先将学习率由0.0001改为0.01，再来训练和评估一次，这回的输出结果如下：

$go build
$./demo
Epoch 1: Weights: [0.009191300234460844 0.009159461537409297], Bias: 0.034000, MSE: 124080.000000
Epoch 2: Weights: [0.018380768863390594 0.01831709148135162], Bias: 0.067997, MSE: 124053.513977
Epoch 3: Weights: [0.02756840625241513 0.027472890197452842], Bias: 0.101990, MSE: 124027.033923
Epoch 4: Weights: [0.03675421276708735 0.036626858051265865], Bias: 0.135980, MSE: 124000.559834
Epoch 5: Weights: [0.04593818877288719 0.0457789954082706], Bias: 0.169966, MSE: 123974.091710
Epoch 6: Weights: [0.055120334635221604 0.05492930263387402], Bias: 0.203949, MSE: 123947.629550
...  ...
Epoch 996: Weights: [47.520035679041236 44.407936879025506], Bias: 339.984720, MSE: 44.287037
Epoch 997: Weights: [47.521568654779436 44.406403906767075], Bias: 339.984872, MSE: 44.286092
Epoch 998: Weights: [47.523101572396406 44.404870992560404], Bias: 339.985024, MSE: 44.285147
Epoch 999: Weights: [47.524634431895045 44.40333813640399], Bias: 339.985174, MSE: 44.284203
Epoch 1000: Weights: [47.52616723327823 44.401805338296306], Bias: 339.985322, MSE: 44.283259
Trained Weights: [47.52616723327823 44.401805338296306]
Trained Bias: 339.985322
Sample 1: Predicted Value: 216.742422, Actual Value: 210.000000
Sample 2: Predicted Value: 239.923439, Actual Value: 230.000000
Sample 3: Predicted Value: 269.738984, Actual Value: 260.000000
Sample 4: Predicted Value: 302.871794, Actual Value: 310.000000
Sample 5: Predicted Value: 336.004604, Actual Value: 340.000000
Sample 6: Predicted Value: 369.137414, Actual Value: 370.000000
Sample 7: Predicted Value: 402.270225, Actual Value: 400.000000
Sample 8: Predicted Value: 435.403035, Actual Value: 430.000000
Sample 9: Predicted Value: 468.535845, Actual Value: 460.000000
Sample 10: Predicted Value: 501.668655, Actual Value: 490.000000
Mean Squared Error: 54.966611

这回我们看懂，训练后的模型在测试集上的预测结果与实际标签值非常接近，可以看到对超参learningRate的调整见效了！

当然如果不调整learningRate，通过调节epochs到一个更大的值可能也能达到这个效果，但却要耗费更多的算力和等待时间。

4. 小结

在这篇文章中，我们在解决线性回归问题时并未引入神经网络的概念，其实基于神经网络也可以解决线性回归问题，并且一个线性回归模型可以看成是一个单层的全连接神经网络。

本文涉及的源码可以在这里[15]下载 - https://github.com/bigwhite/experiments/blob/master/go-and-nn/linear-regression

本文的数学公式均由https://www.latexlive.com/基于latex语法在线生成。

本文中的部分源码由OpenAI的GPT-4o生成。

5. 参考资料

• 《人工智能：现代方法（第4版）》[16] - https://book.douban.com/subject/36152133/
• 《零基础学机器学习》[17] - https://book.douban.com/subject/35264202/
• 《动手学深度学习2nd-pytorch版》[18] - https://zh-v2.d2l.ai
• 《深度学习进阶：自然语言处理》[19] - https://book.douban.com/subject/35225413/
• 《机器学习：Go语言实现》[20] - https://book.douban.com/subject/30457083/
• 《深度学习入门2：自制框架》[21] - https://book.douban.com/subject/36303408/
• 《GO语言机器学习实战》[22] - https://book.douban.com/subject/35037170/