批评不仅能让人进步,也能让大模型的能力提升。
OpenAI就用这个思路造了个“找茬模型”CriticGPT。非常巧合的是,就在CriticGPT放出的前几天,北大联合千问等团队以类似的思路设计出了“数学专用版”CriticGPT。
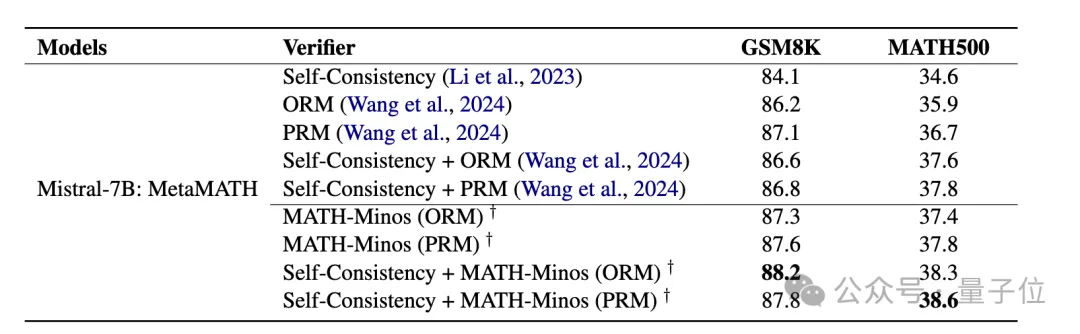
在无需训练的设置下,验证器能够在推理时辅助模型在GSM8K上的准确率从86.6%提升到88.2%。
在GSM8K数据集上,它可以让模型的准确率从86.6%提升到88.2%。

CriticGPT的核心思路是在代码中故意设置bug并进行详细标注,然后用得到的数据训练出会debug的模型。
北大团队发现,这种方法不仅在代码当中有用,也能帮助语言模型解决数学问题。
于是团队利用相似的思路,把代码换成数学问题,推出了“数学版CriticGPT”——Math-Minos。
用GPT4逐步提出修正意见
在数学推理领域,验证解决方案的正确性,是确保推理质量的关键步骤。
然而,现有的数学验证器大多依赖于二元分类标签进行训练,这种方式在提供正确或错误原因的解释上存在明显不足,无法给验证器提供足够充分的监督信号来训练。
Math-Minos则克服了这一局限,提供了更深入的解释,极大地丰富了验证器的训练信息。
它引入了逐步的自然语言反馈作为理由标签,不仅指出了解决方案的正误,还能逐步分析出错误的原因。
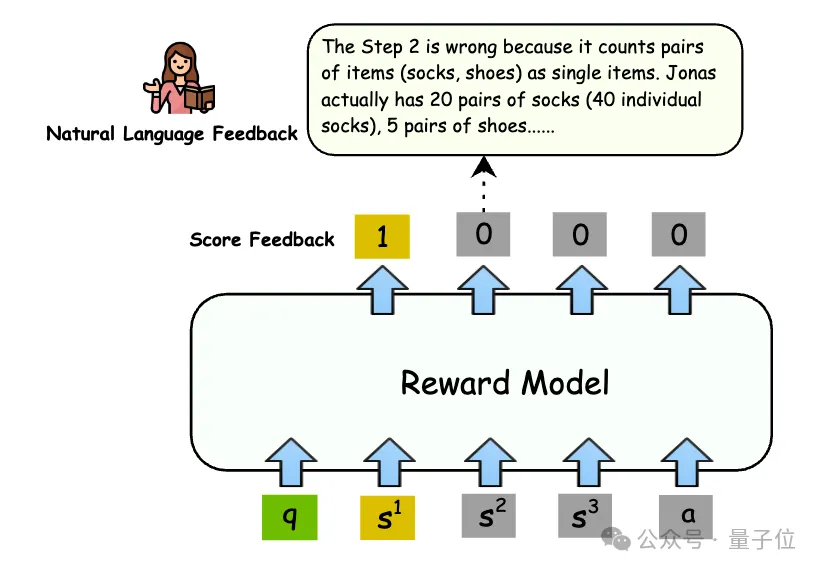
在自然语言反馈的获取上,研究团队一开始使用GPT-4生成训练数据,但通过实验发现,即使是GPT-4,在逐步评价数学推理任务时也会出现一定比例的错误。
为了一定程度避免这个问题,研究人员通过在提示中引入步骤级别的二元分类标签,简化了GPT-4的任务,使得GPT-4能够更准确地生成评估。
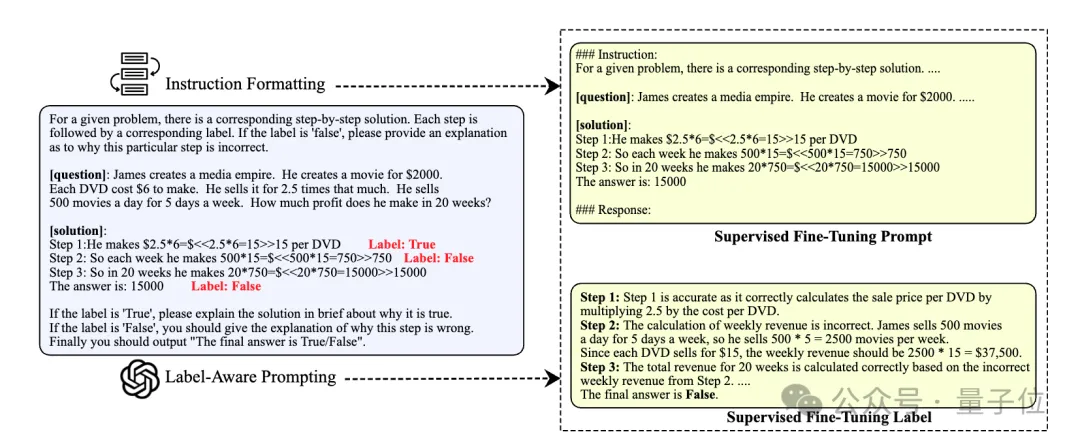
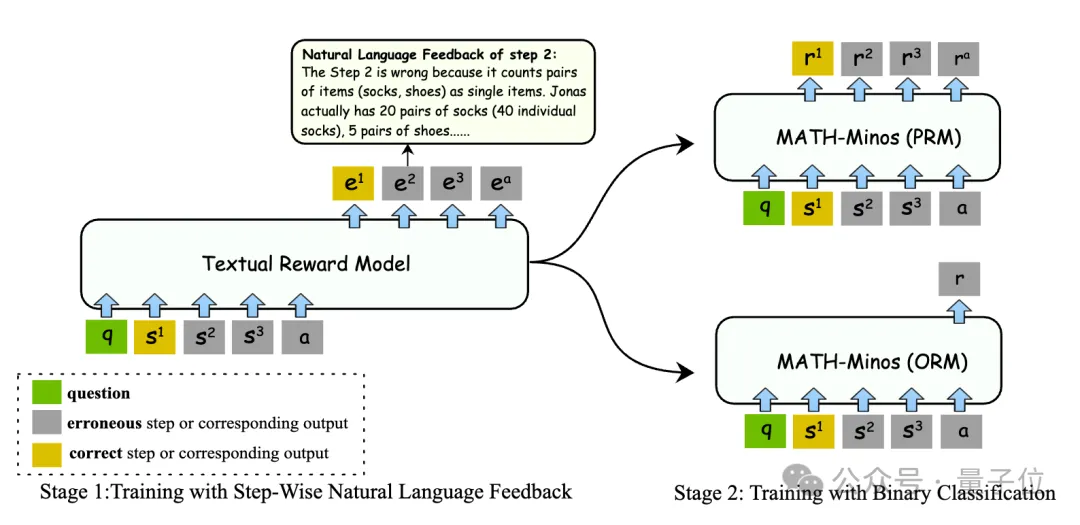
首先,通过监督式微调,使用自然语言反馈作为训练数据,有效提升了模型的评估能力。
其次,通过标准的ORM(Outcome Reward Model,输出奖励模型)和PRM(Process Reward Model,过程奖励模型)训练,实现了高效的推理,这种做法有两个好处。
一是通过两阶段训练,可以将二分类数据和监督微调数据解耦。
由于监督信号的稀疏性,训练二分类的数据往往远多于监督微调的数据,而研究发现,仅需要少量的监督微调数据,就可以很大程度提升模型的评估能力。
另一方面,在验证器进行验证时,不需要显示地生成自然语言反馈,让推理过程更高效。
ORM任务表现明显提升
总得来看,研究人员在训练阶段添加了30K的自然语言反馈数据,为Mistral-7B验证器带来了数学能力的提升,在Best-of-256的实验设置下:
在ORM的设置下,MATH-Minos将Mistral-7B的准确率在GSM8K数据集从86.2%提升到87.3%,在MATH数据集从35.9%提升到37.4%。
在PRM的设置下,MATH-Minos将Mistral-7B的准确率在GSM8K数据集从87.1%提升到87.6%,在MATH数据集从36.7%提升到37.8%。
在与Self-Consistency结合的设置下,MATH-Minos将Mistral-7B的准确率在GSM8K数据集从87.1%提升到88.2%,在MATH数据集从37.8%提升到38.6%。
在ORM和PRM任务设置中,Math-Minos均展现出了优越的性能,特别是在ORM设置中,其改进更为显著。
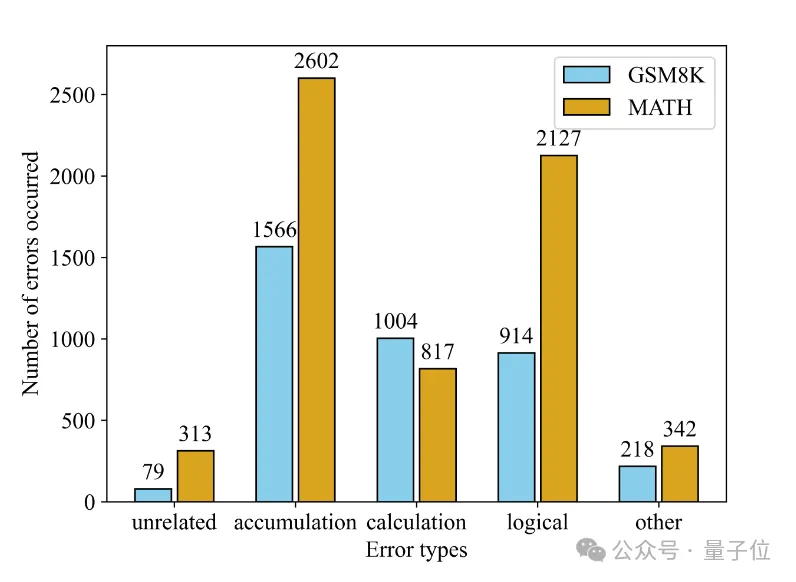
另外,研究团队还对生成器在步骤级别产生的错误进行了深入分析,将其归类为五种类型——无关错误、累积错误、计算错误、逻辑错误和其他错误。
分析结果表明,在多步骤推理中,步骤错误的可能原因有很多种,而且模型在这些错误类型中都有可能出错,这进一步强调了引入自然语言反馈来指导模型学习的重要性。
实验发现,在两个数据集上,累积错误(即一个步骤的错误很可能直接导致所有后续步骤的错误)在所有错误类型中占到的比例最高。
不同数据集上的错误分布也有不同的特点,在相对简单的GSM8K上,计算错误更多;在更困难的MATH数据集上,逻辑错误更多。
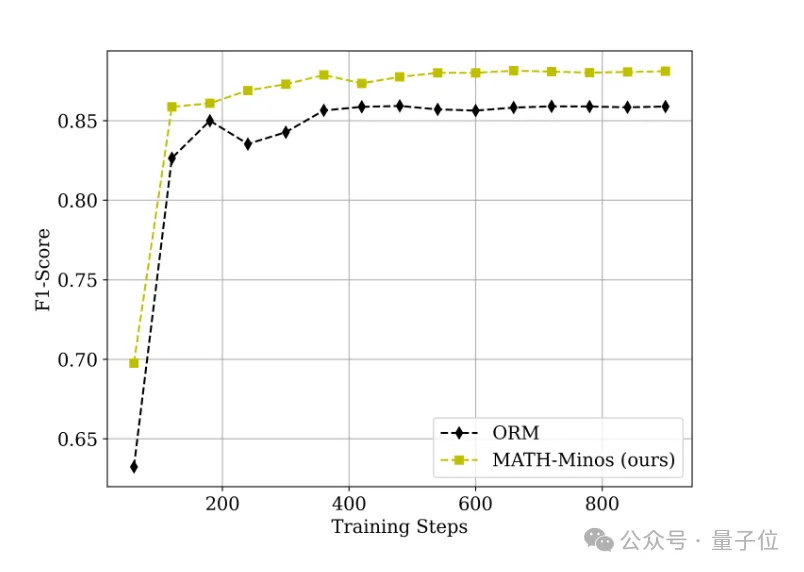
通过构建元评估集,研究团队评估了验证器在没有生成器影响下,准确判断最终答案的能力。
结果显示,Math-Minos在训练过程中的元评估一致优于传统的ORM,并且展现出更快的收敛速度和更精准的判断能力。
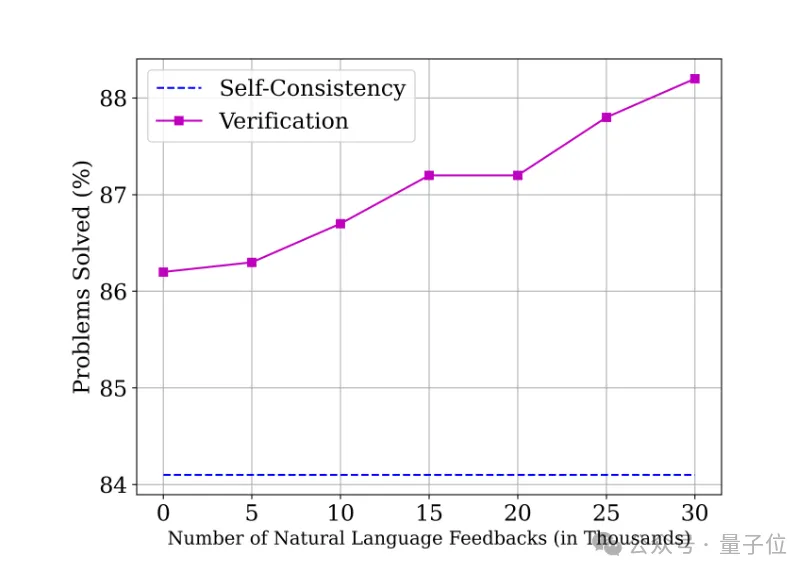
同时实验结果也表明,Math-Minos具有很强的Scale Up的潜力。
总之,Math-Minos的开发不仅提升了数学验证器的性能,更为自然语言处理领域提供了一种新的训练范式。
研究团队希望这项工作能够启发未来研究,探索自然语言反馈与分类式验证器的潜在整合,推动大型语言模型在复杂推理任务上的能力。
论文地址:https://arxiv.org/abs/2406.14024
GitHub:https://github.com/KbsdJames/MATH-Minos