大家好，我是小风哥，今天简单聊聊字符串匹配kmp算法。
字符串匹配是计算机科学中非常基础的操作，给定两个字符串a和b，我们需要判断字符串a是否包含字符串b。
图片
像你我这样的普通程序员能想到的最简单方法是这样的，用字符串b不断去匹配每个主串中的子串。
假设给定这样两个字符串：
图片
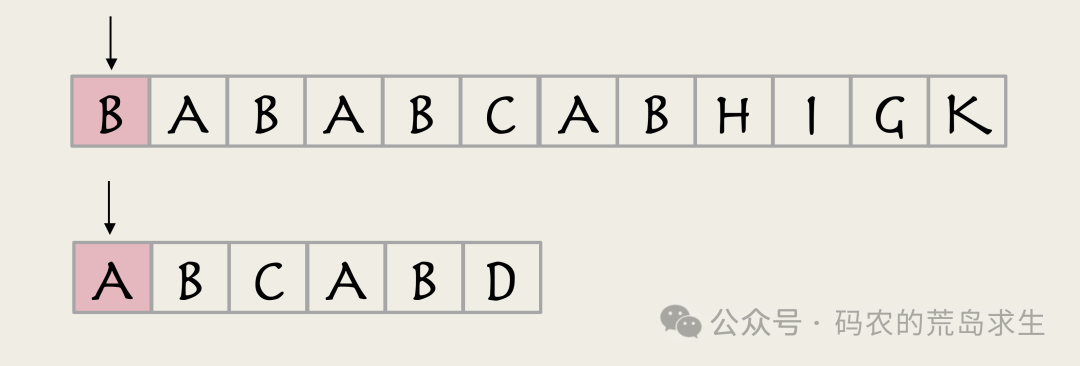
首先从主串的第一个位置和子串的第一个位置去匹配，我们发现A和B不相同：
图片
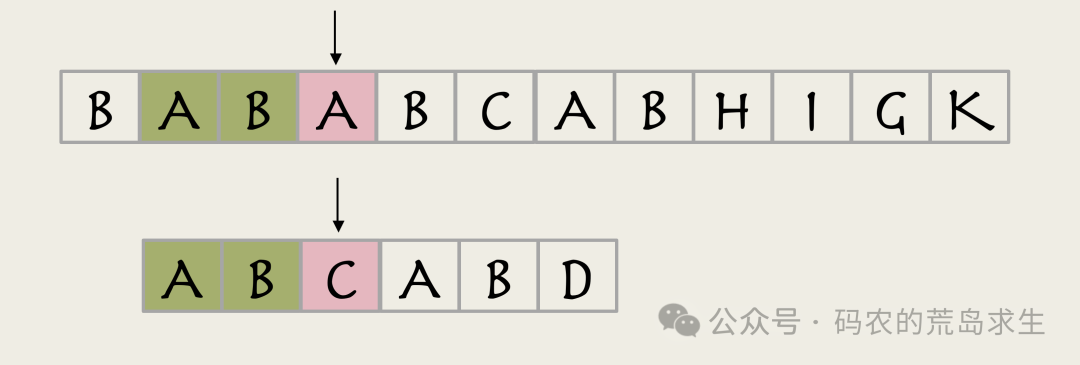
因此主串指针后移一位，子串重新从最第一个字符开始匹配。
图片
这时我们发现A和C不同，因此匹配失败。
图片
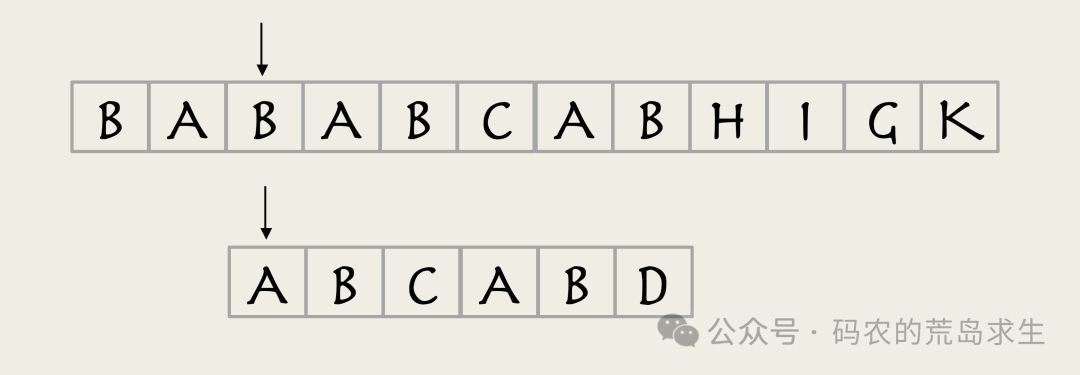
主串指针回退到第三个字符，子串重新从第一个字符开始匹配。
图片
此时B和A又不同，重复上述过程。
这次成功找到多个相同的字符，但最后一个字符匹配失败：
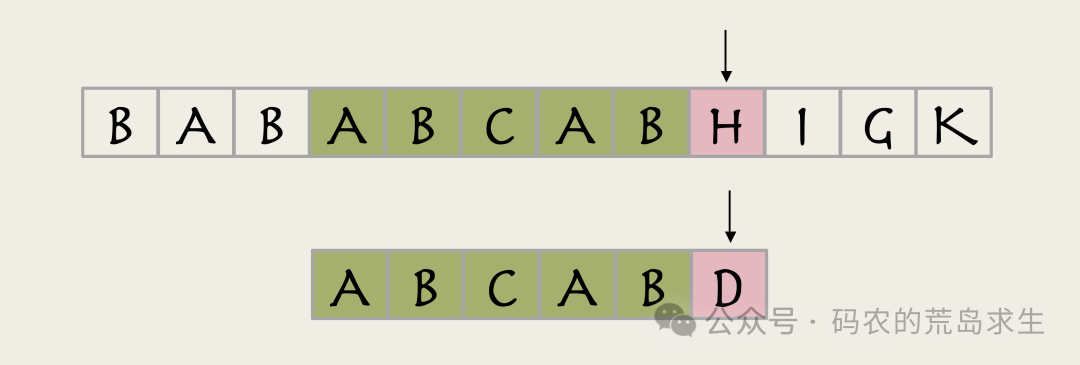图片
按照我们的算法，主串指针需要回退到第5个字符重新匹配。
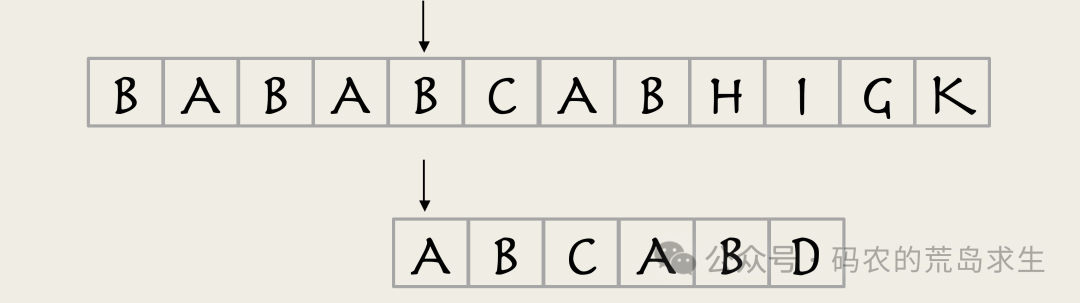图片
这就是你我这种肉体凡胎能想到的算法，时间复杂度是O(mn)，效率低下的原因当然是主串指针需要回退。
然而有三位大神不是这么想的，它们跳出来凡人的思考方式发明了一种极具创意的算法，由于是三个人同时发现，因此这个算法取了三人名字的首字母，这就是著名的kmp算法。
图片
看到这里相信你就能明白为什么这个算法很难掌握了吧，难是正常的，觉得不难才不正常，如果你能无师自通搞定kmp算法，那么早出生几十年你也能和大师们并驾齐驱供我等凡夫俗子瞻仰。
废话不多说，接下来就让我们领略一下大师的非凡境界。
注意看这个主串指针，大师们思考的第一个问题就是，主串指针是否有必要回退，这是最关键最核心的问题。
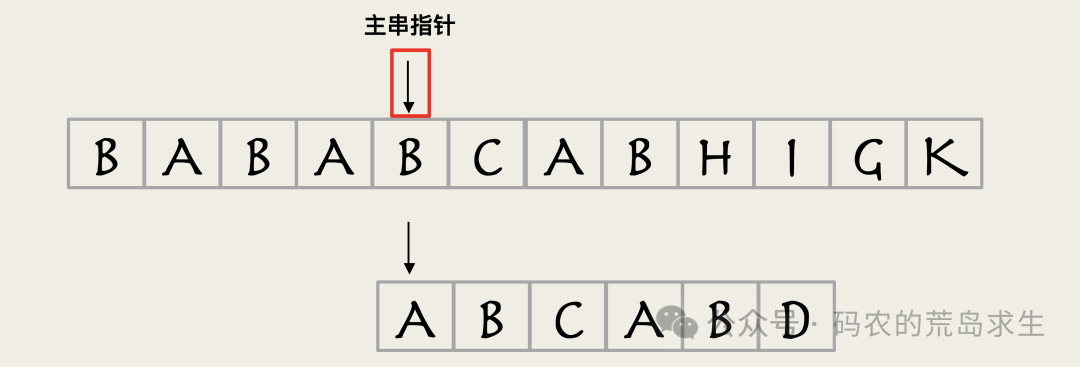图片
让我们回到刚才部分匹配的示例。
主串指针是否需要需要回退呢？我们思考两种可能。
第一种可能，即使能匹配成功，匹配成功的起始位置也在主串指针H及以后，在这种情况下主串指针不需要回退。
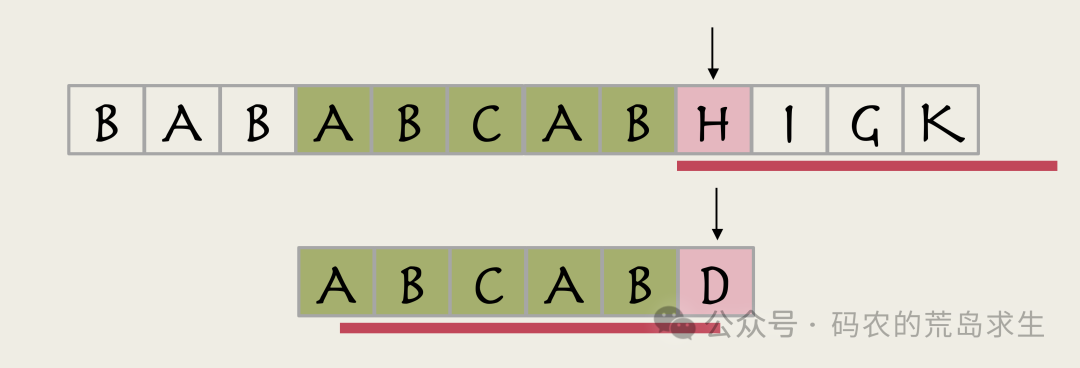图片
第二种可能，匹配成功的起始位置经过主串指针H：
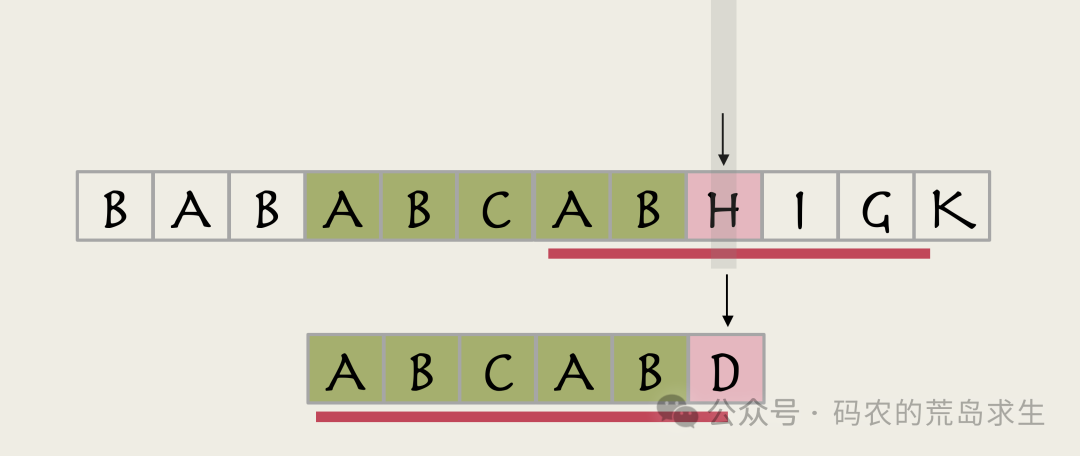图片
在这种情况下，主串指针之前的两个字符A和B一定是成功匹配了的：此时我们只需要比较主串指针H及以后的位置即可。
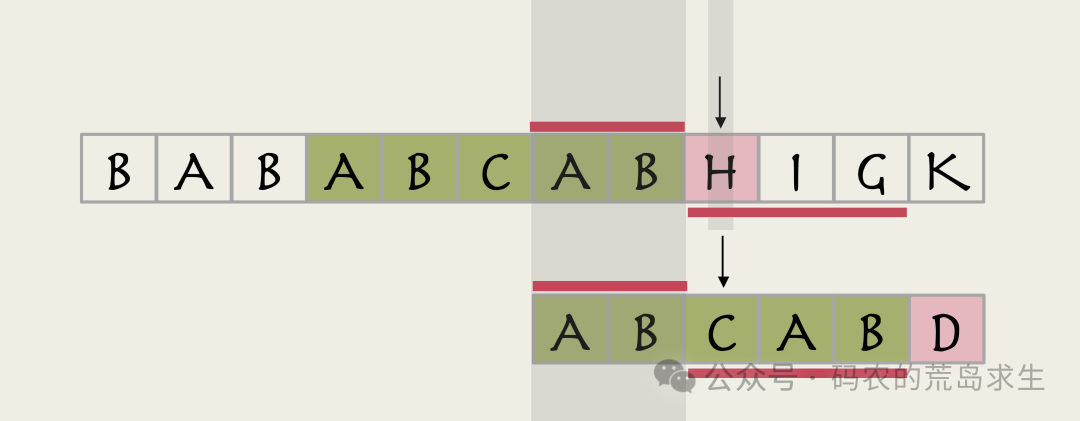图片
只有这么两种可能。
因此可以看到，主串指针根本就没有必要回退。
现在我们知道了主串指针不需要回退，那么子串指针该从哪里开始匹配呢？从头开始吗？
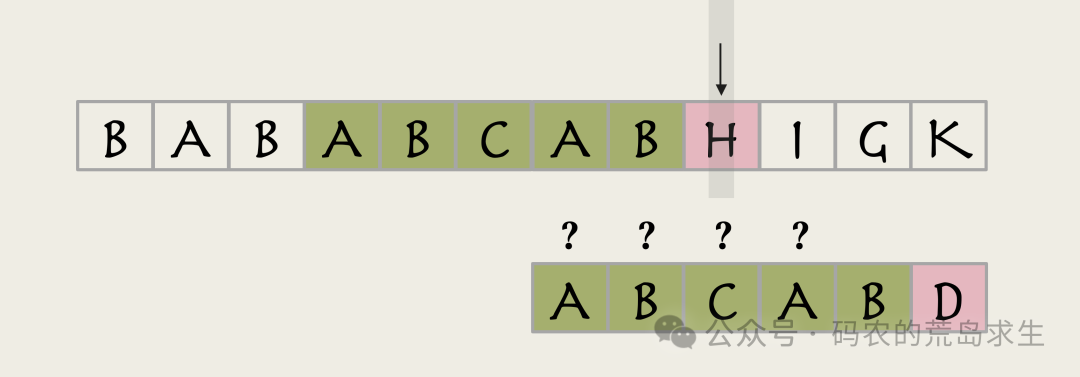图片
注意看我们刚才提到的第二种可能，匹配成功的起始位置经过主串指针H，在这种情况下，主串指针之前的两个字符A和B一定是成功匹配了的，这意味着什么呢？
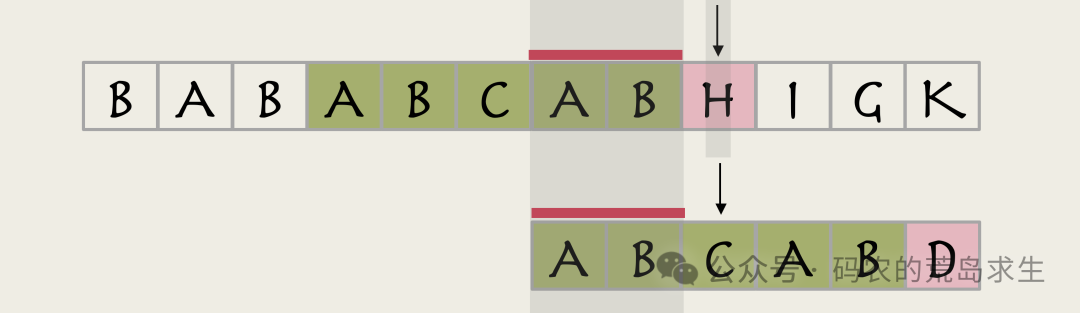图片
这意味着AB是这个字符串的后缀：
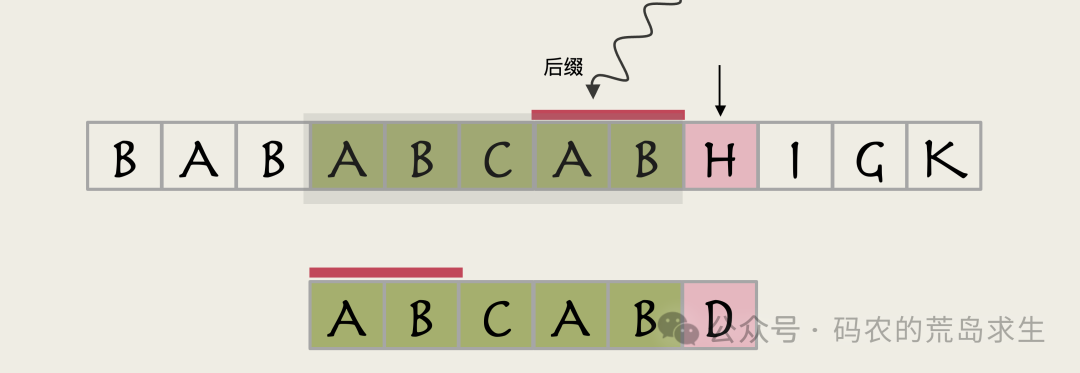图片
AB是这个字符串的前缀：
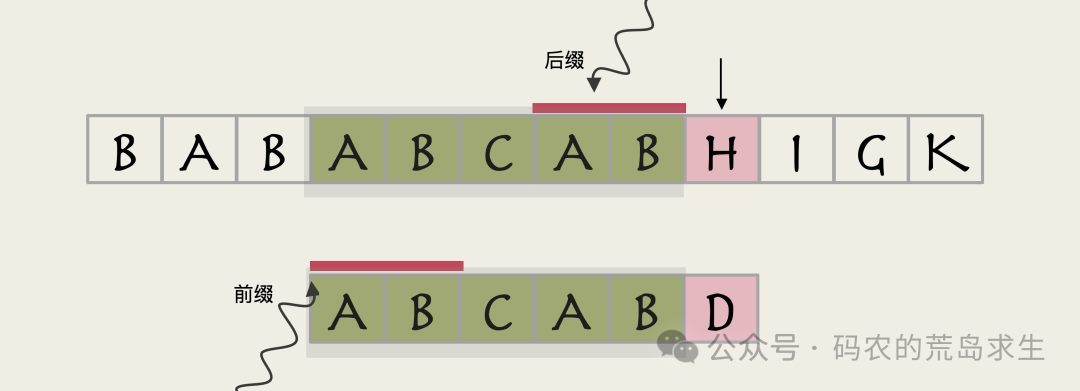图片
不要忘了这两个字符串是成功匹配了的：
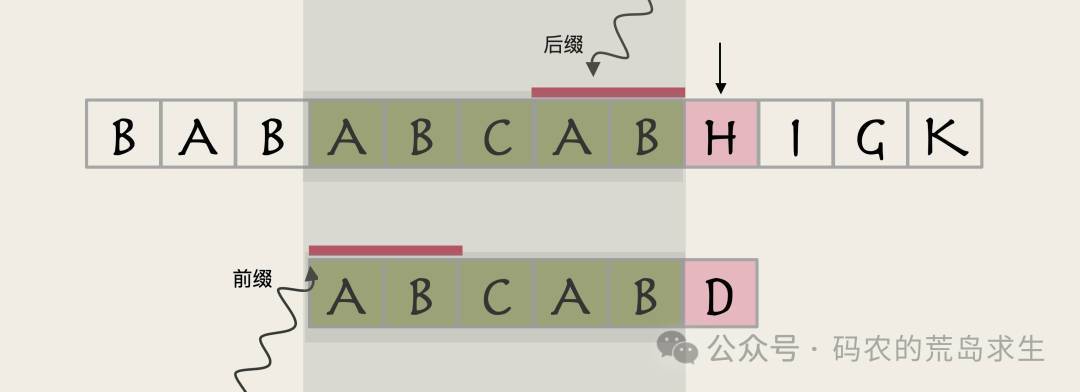图片
也就是说这是两个完全相同的字符串，这就意味着AB是成功匹配字符串的相同前后缀。
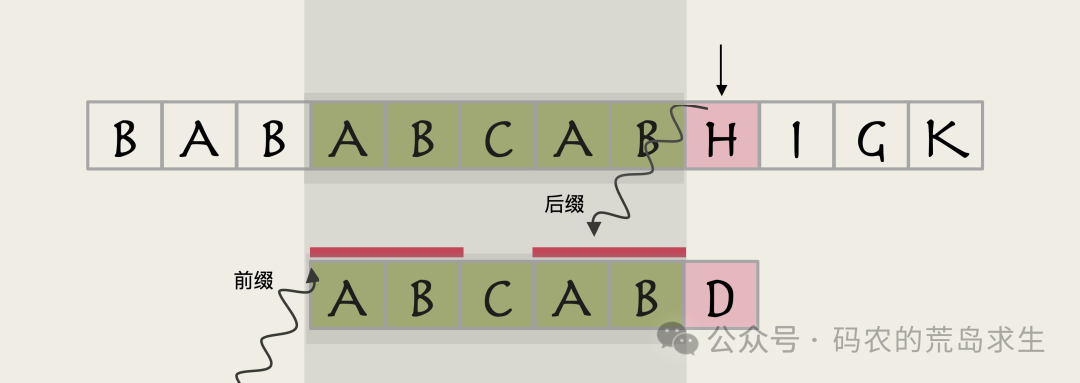图片
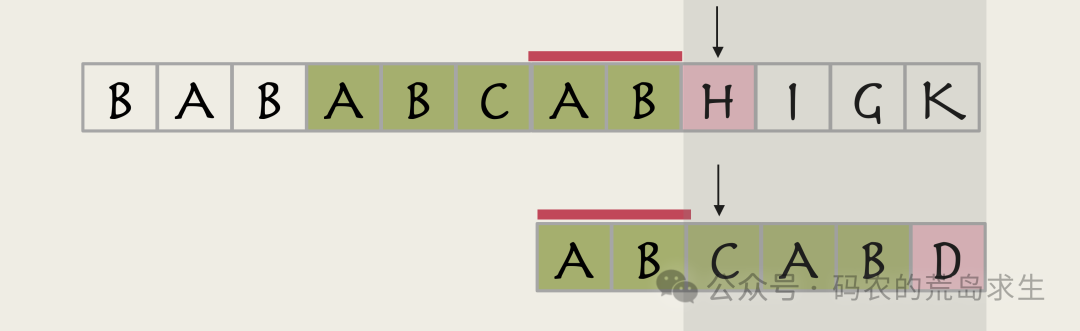
这样子符串指针也不需要回退到起始位置，而是从共同前后缀的下一个位置开始匹配即可。
图片
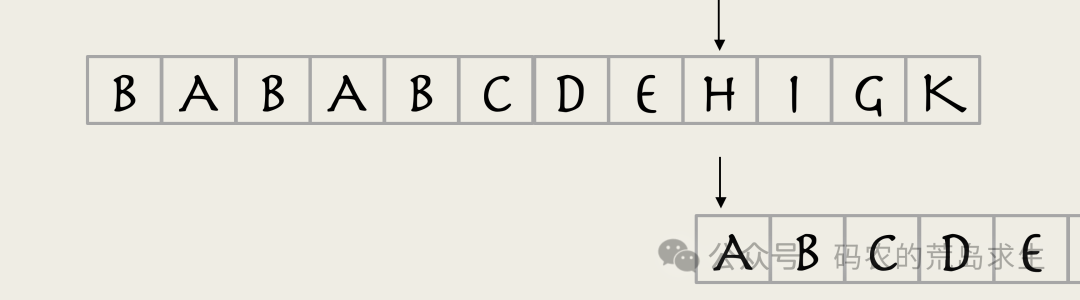
而对于部分匹配的子串根本不存在共同前后缀的情况，
图片
我们直接从子串起始位置进行匹配。
图片
可以看到，由于主串指针不回退，这大幅提高了算法的效率。
想要实现这样的算法，关键是怎样计算出部分匹配子串的共同前后缀。
因此我们来到了第二个核心问题。
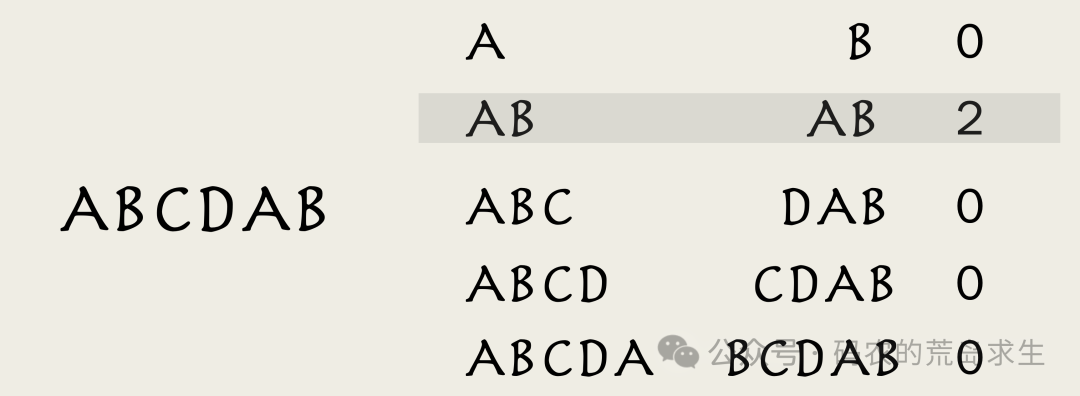
我们以ABCDAB为例来讲解。
这是长度为1的前后缀，这是长度为2的前后缀，以此类推。
图片
可以看到，在所有的前后缀中，相同前后缀的最大长度是2。
图片
我们记下来。
实际上我们需要把所有子串的相同前后缀都计算出来。
对于ABCDA这个子串来说，相同前后缀长度是1，因为两个A是相同前后缀。
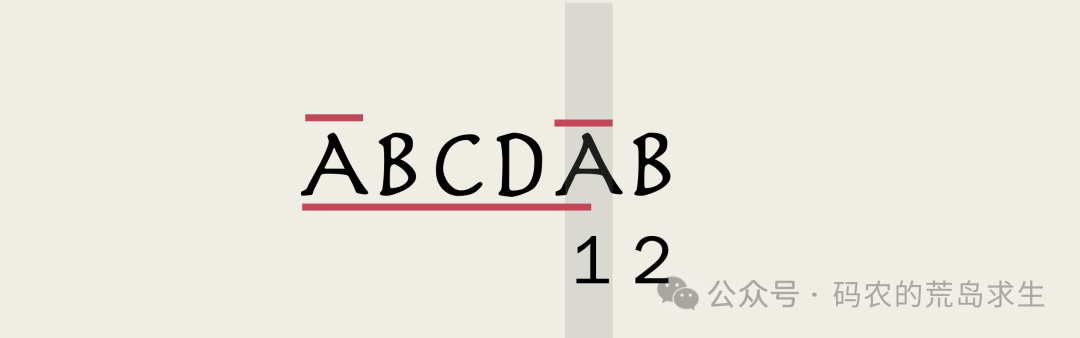图片
而对于ABCD这个子串来说，相同前后缀的长度是0，也就是没有相同的前后缀。
其它也一样。
这样我们就到了一个数组，通过查找这个数组我们能知道任意子串的共同前后缀长度。
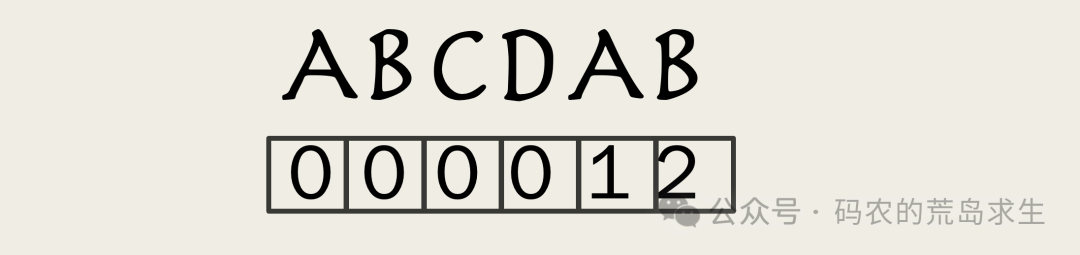图片
这个数组在很多资料中被称之为next数组。
有了next数组就简单了。
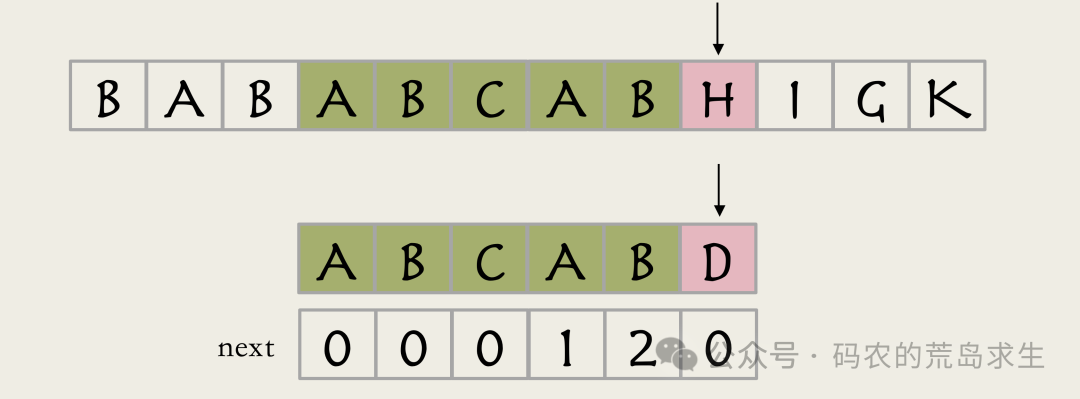
假设此时我们发现两个指针指向的字符不同，接下来只需要简单查找next数组：
图片
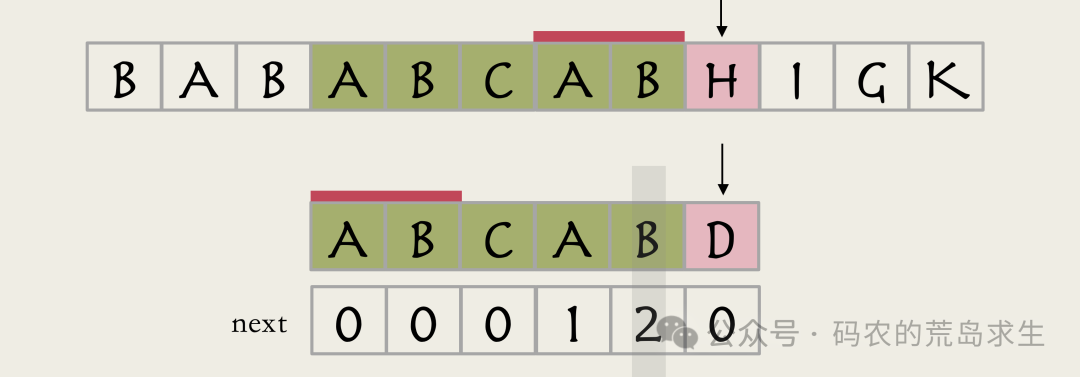
发现已匹配部分的相同前后缀长度是2：
图片
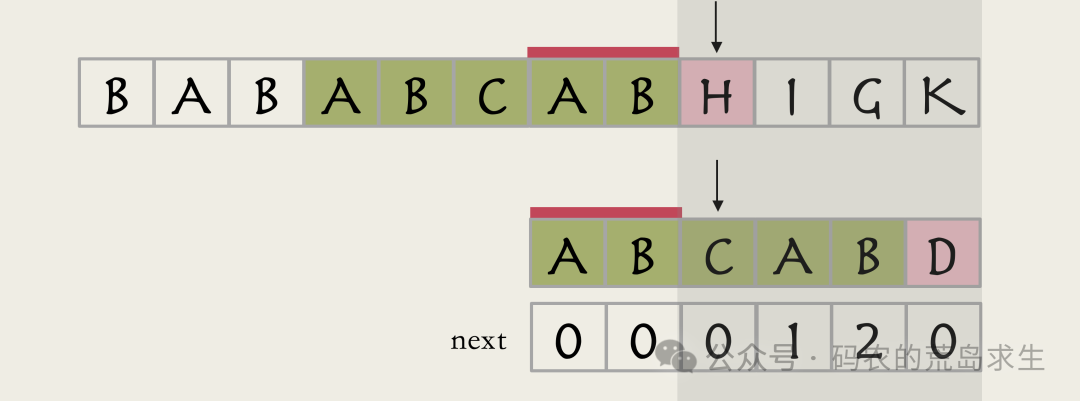
因此主指针不动，子串指针移动到相同前后缀的下一个位置继续去匹配即可。
图片
可以看到，只要我们能得到next数组，就可以在线性时间复杂度内解决问题。
这里，我们来到了第三个核心问题，那就是该怎样高效计算出next数组。
假设此时我们已经计算出了这个子串的共同前后缀，也就是长度为n的这两个部分。
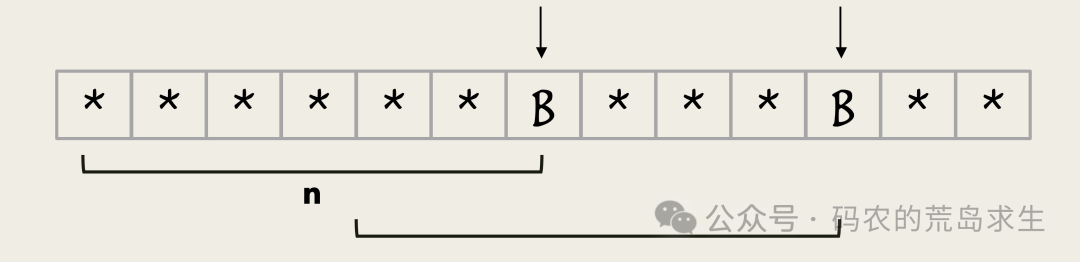图片
接下来计算下一个位置的最长前后缀，我们只需要分别后移两个指针，然后比较字符是否相等，这里有两种可能。
第一种可能是接下来的字符相同，那么这个子串的最长相同前后缀的长度就是n+1。
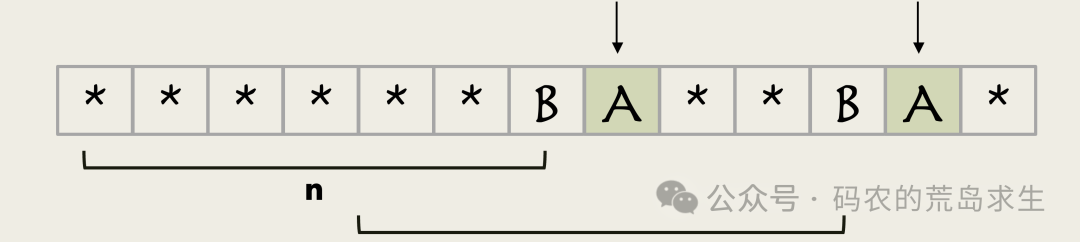图片
然后写到next数组即可，这很好理解。
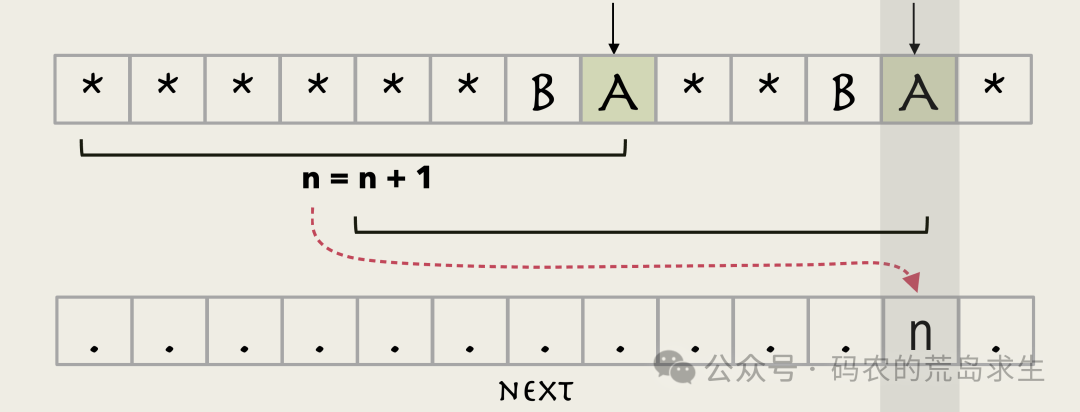图片
但是如果下一个位置的字符不相等该怎么办呢？
注意接下来是整个算法最核心的，也是最具技巧的地方。
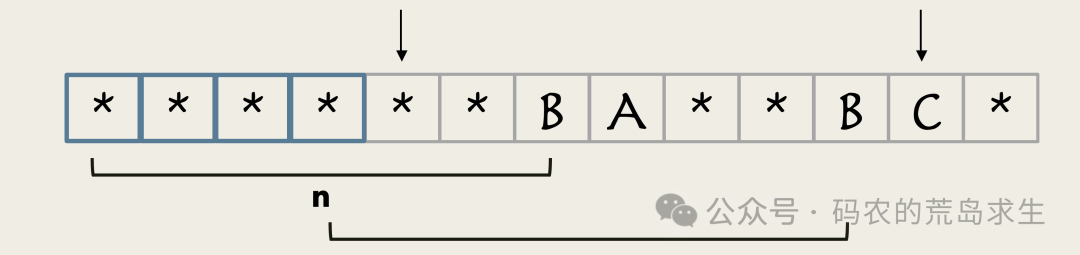
如果接下来的两个字符不相等，那么前面的这部分绝无可能形成最长前后缀。
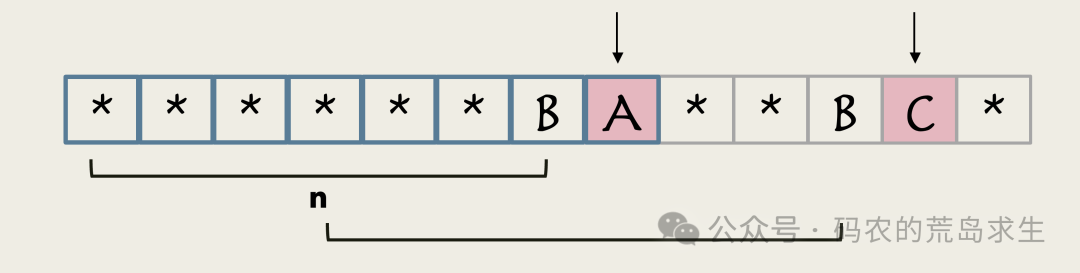图片
因此我们只能找一个更短的。
图片
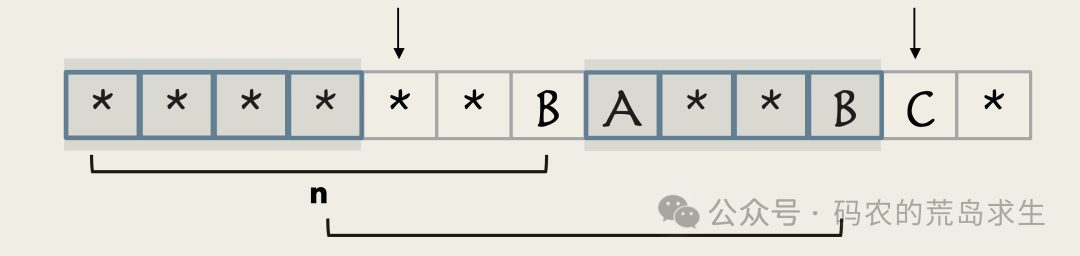
如果能找到一个更短的，这就意味着这两部分会形成一个共同前后缀。
图片
然后我们继续比较下一个字符就可以了，这就回到最初的问题。
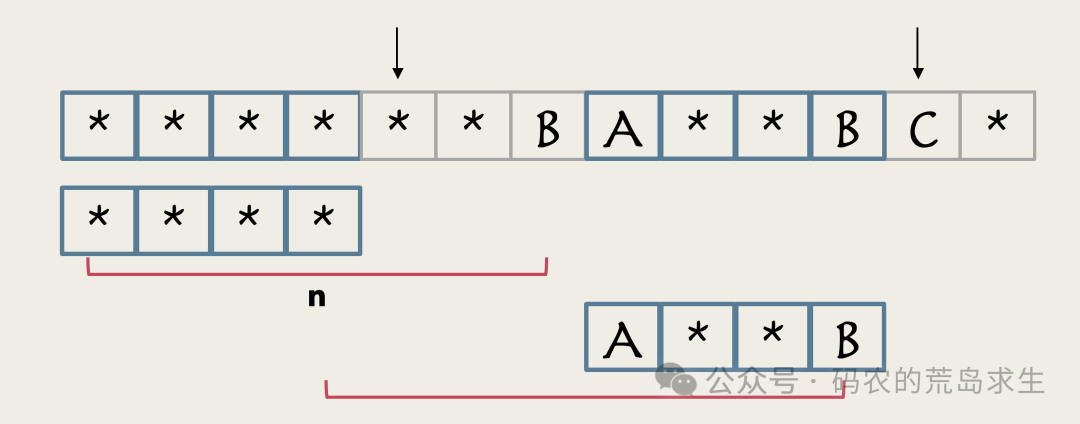
那么这两部分相同意味着什么呢？
不要忘了红色部分是我们之前找到一个共同前后缀，也就是说红色部分的子串完全相同。
图片
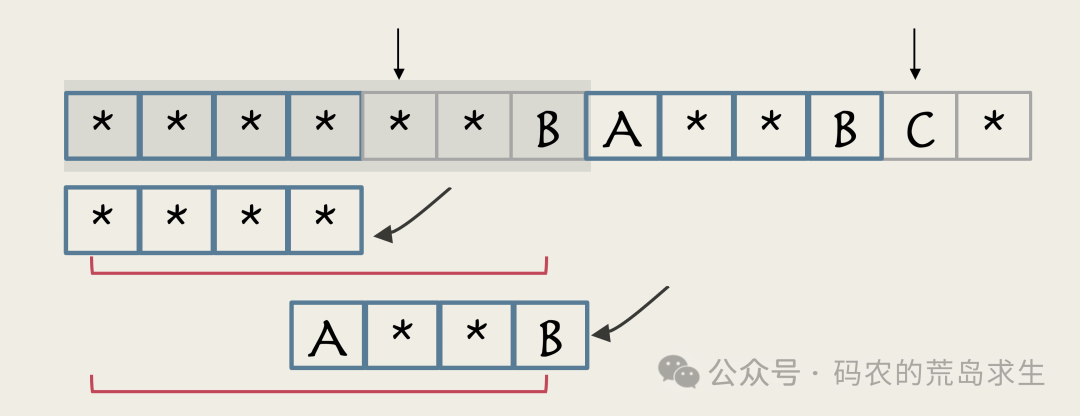
而现在这两个子串也相同，这就意味着这两个更小的子串其实是红色部分子串的最长前后缀。
图片
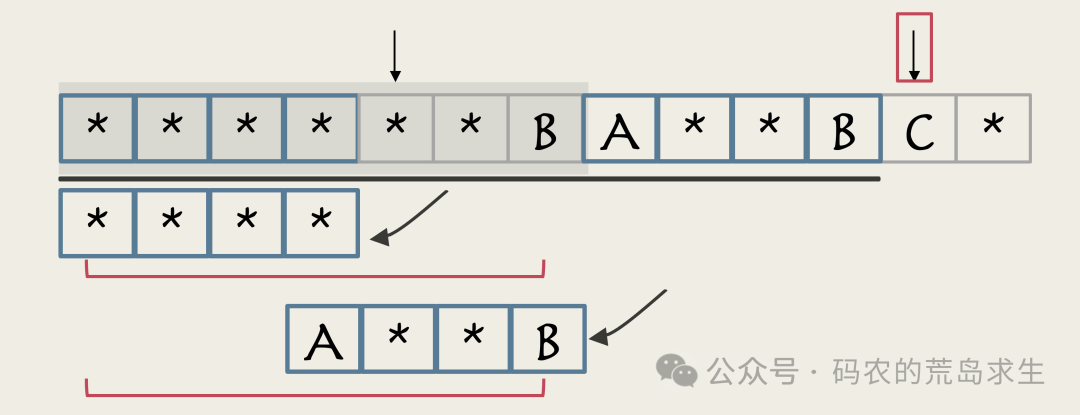
不要忘了，此时我们的指针已经来到了这里，前面这部分的next数组已经计算出来了。
图片
通过查next数组，我们可以快速得到更短前后缀的长度。
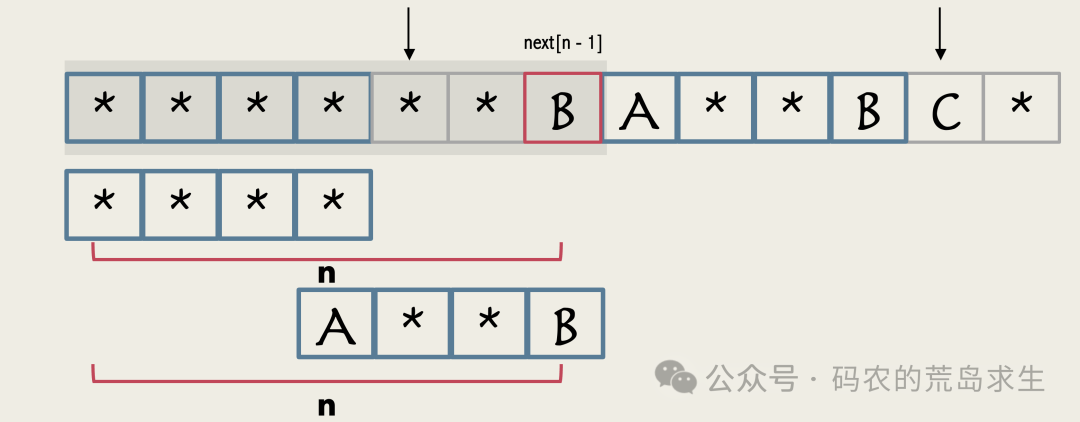
既然红色部分的长度是n，那么更短前后缀的长度其实就是next[n-1]。
图片
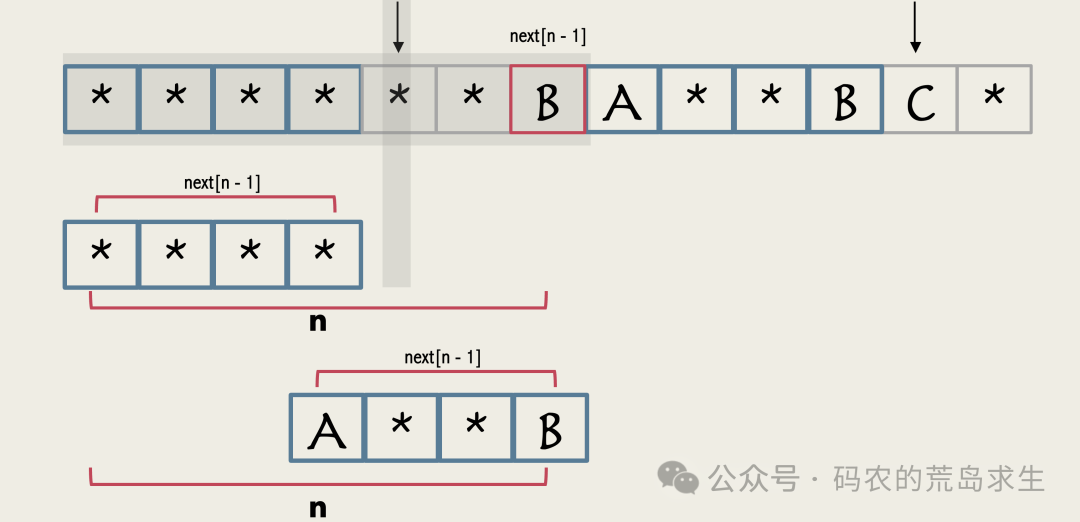
再来看下，红色部分的长度是n，那么更短前后缀的长度是next[n-1]。
也就是这个位置。
图片
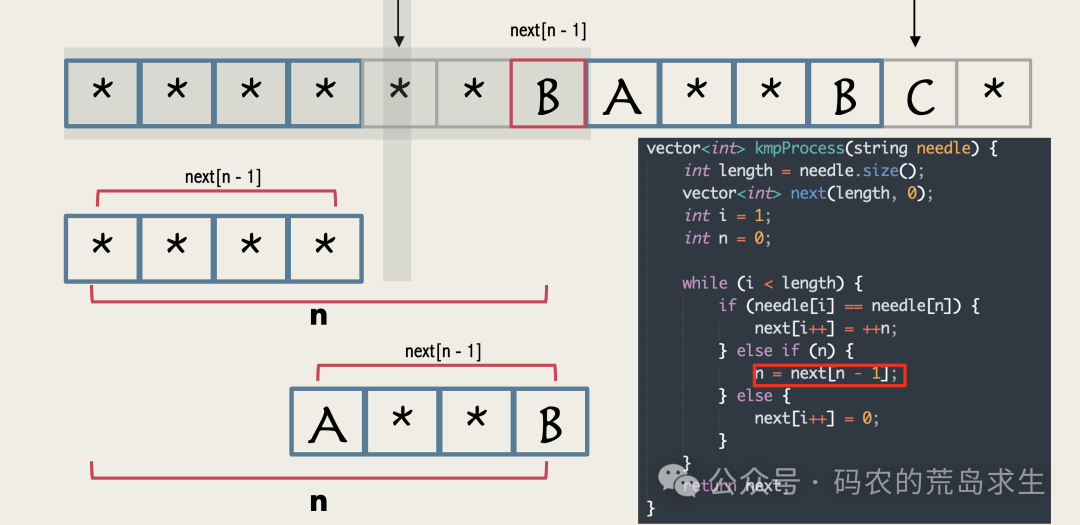
这就是计算next数组源代码中n=next[n-1]这句话的含义。
图片
现在我们再来看一遍整个过程。
此时两个字符的长度不等，那么我们只需要简单查一下next[n-1]：
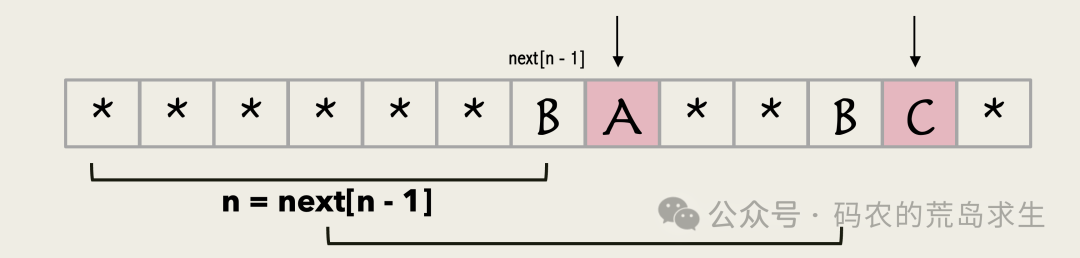图片
这就是更短的前后缀长度，假设是4。
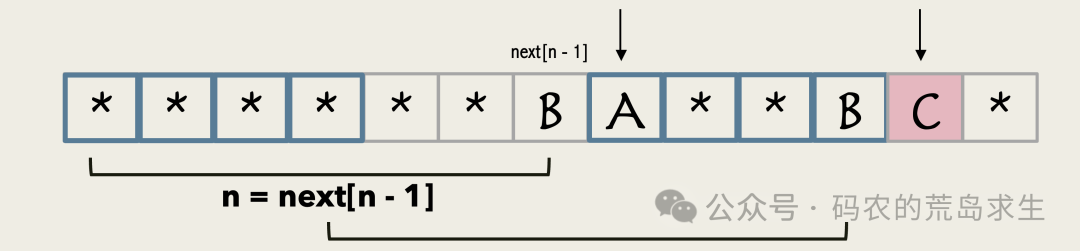图片
此时前一个指针回退到位置4，继续比较下一个字符即可。
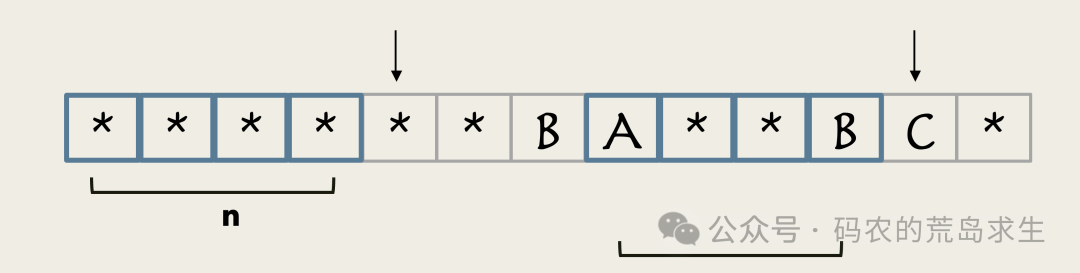图片
如果下一个字符相同，那么当前位置next数组的值就是n+1。
而如果下一个字符不相同，我们继续查找next[n-1]，然后前一个指针回退，继续比较下一个位置即可。
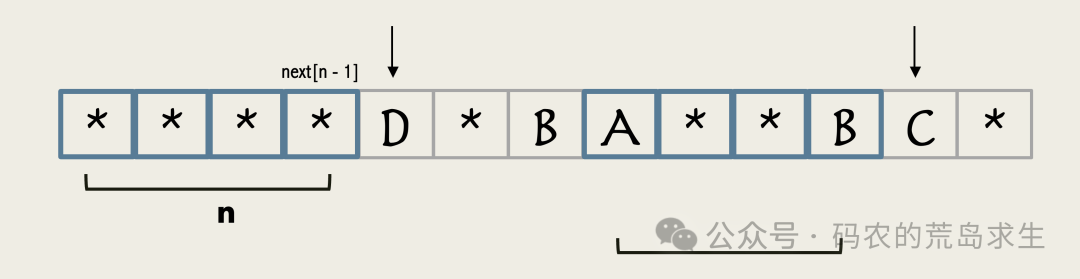图片
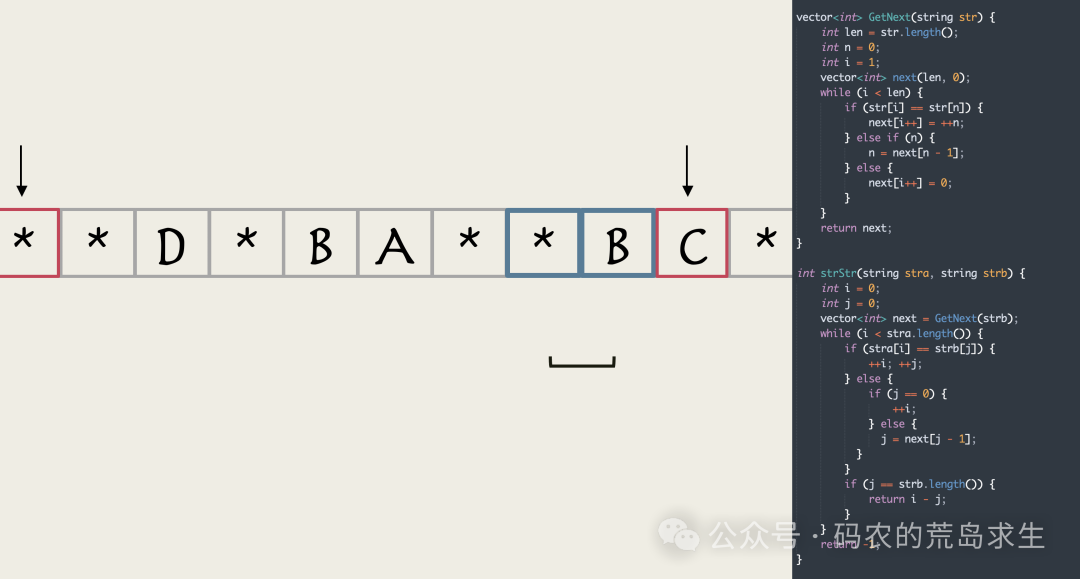
这就是完整的kmp算法实现，可以看到整个代码实际上只有30多行。
如果你能在50多年前写出这几行代码，你也能和它们并列，在计算机科学史上会留下你的一笔。
图片
好啦，以上就是本期全部内容。
