本文经计算机视觉研究院公众号授权转载,转载请联系出处。

- 论文地址:https://arxiv.org/abs/2402.17709
- 项目主页:https://github.com/GraphPKU/Case_or_Rule
- 论文标题:Case-Based or Rule-Based: How Do Transformers Do the Math?
Case-based or rule-based?
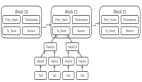
人类可以轻松地学习加法的基本规则,例如竖式加法,并将其应用于任意长度的新的加法问题,但 LLMs 却难以做到这一点。相反,它们可能会依赖于训练语料库中见过的相似样例来帮助解决问题。来自北京大学张牧涵团队的 ICML 2024 论文深刻研究了这一现象。研究者们将这两种不同的推理机制定义为 “基于规则的推理”(rule-based reasoning)和 “基于样例的推理”(case-based reasoning)。图 1 展现了两种推理机制在遇到同一个加法问题时,采用的不同模式。
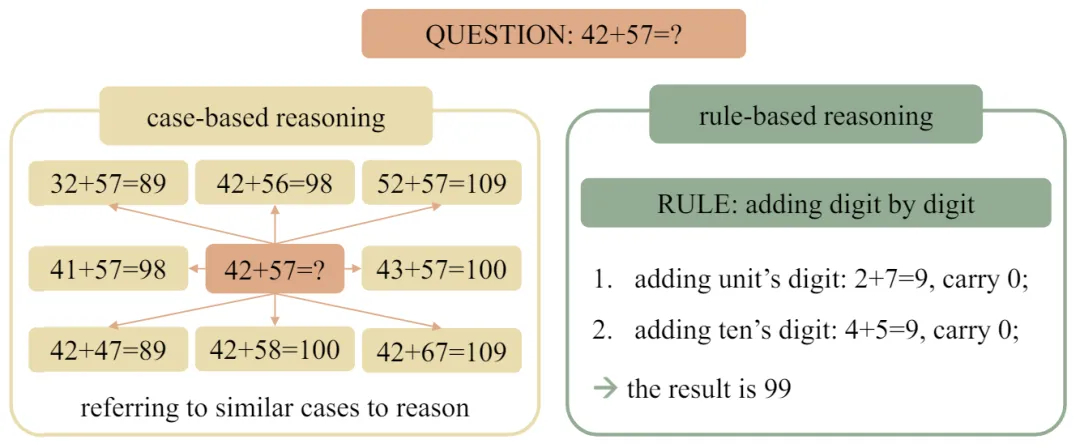
图 1:case-based reasoning 与 rule-based reasoning 示意图
由于 rule-based reasoning 对于获得系统性的泛化能力 (systematic generalization) 至关重要,作者在文章中探讨了 transformers 在数学问题(例如 "")中到底是使用何种推理机制。为了测试模型是否依赖特定样例来解决问题,作者使用了 Leave-Square-Out 方法。主要思想是首先需要定位模型可能依赖的训练集中的样例,然后将它们从训练集中移除,以观察它们是否影响模型的测试性能。对于数学推理,作者的假设是,在解决某个测试样本时,transformers 倾向于依赖与测试样本 “接近” 的训练样本来进行推理。因此,作者在样本的二维空间中挖掉了一块正方形作为测试集(test square)。根据假设,若模型在做 case-based reasoning,且模型依赖的是与 test sample 距离较近的 training sample 来做推理,那么模型将无法答对正方形中心附近的 test samples,因为模型在训练集中没有见过接近的样例。
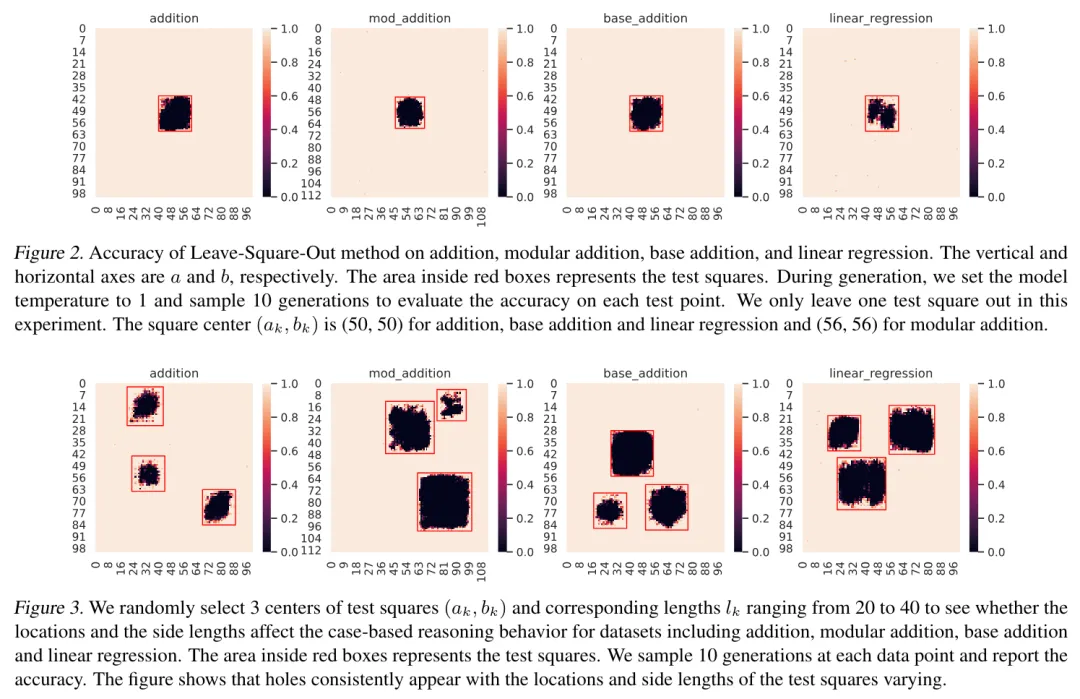
图 2:GPT-2 在加法、模加法、九进制加法、线性回归上利用 Leave-Square-Out 方法进行 fine-tune 后在全数据集上的正确率。其中,红框中的方形区域为测试集,其他部分为训练集合。
通过在五个数学任务(包括加法、模加法、九进制加法、线性回归以及鸡兔同笼问题)的干预实验,transformers 无一例外都表现出了 case-based reasoning 的行为。作者利用 Leave-Square-Out 方法对 GPT-2 进行了 fine-tune,具体的模型表现展示于图 2。可见,测试集内,模型的性能由边界到中心迅速下降,出现了 holes。这说明当我们把 holes 周围的 similar cases 移出训练集时,模型便无法做对 holes 中的 test samples 做出准确推理。也即展现出模型依赖 similar cases 进行推理的行为。为了确保结论的公平性,作者同时利用 random split 方法对数据集进行了训练集 / 测试集的划分,并观察到 random split 下模型可轻易在测试集上达到接近 100% 的准确率,说明 Leave-Square-Out 实验中的训练样例数是足够模型完成推理的,且再次侧面印证了 transformers 在做基于样例的推理(因为 random split 下所有 test samples 都有接近的 training samples)。
Scratchpad 是否会改变模型推理行为?
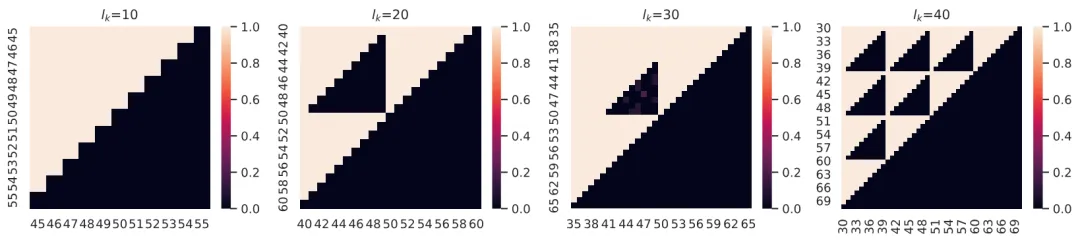
图 3:利用 scratchpad 对 GPT-2 在加法任务上进行 fine-tune 后的模型在 test square 中的准确率。
此外,作者探讨了是否可以通过加入 scratchpad,即引导模型在输出中一位一位地做加法来消除 case-based reasoning 的行为,使模型转向 rule-based reasoning(scratchpad 的具体方法可见图 4)。图 3 展示了利用 scratchpad 对 GPT-2 在加法任务上进行 fine-tune 后的模型在 test square 中的准确率。
一方面,可发现 test square 中仍然有一部分模型无法做对的区域,表现出模型仍然在做 case-based reasoning;另一方面,与不加入 scratchpad 时模型在 test square 中出现整块连续的 hole 的现象相比,模型在使用 scratchpad 时对于训练样例的依赖情况显然发生了变化。
具体而言,test square 中无法做对的区域呈现为三角形,其斜边沿着个位和十位的 “进位边界”。例如,图 3 中自左向右第 2 张图(test square 边长)有两个三角形区域,模型的准确率几乎为零。小三角形表示,模型无法解决如47+48的问题,因为训练集中没有包含十位上进位的步骤(所有四十几 + 四十几的样例都在测试集中)。而对于不涉及十位进位的测试样本,如42+43 ,模型则能够成功,因为它可以从大量其他训练数据中学习到 4+4这个中间步骤(例如)。对于大三角形中的数据而言,模型无法解决例如57+58这样的问题,因为训练集中没有包含十位上需要进位到百位的案例。
这些黑色区域的形状和位置表明,只有当测试案例的每一步在训练集中都出现过时,模型才能够成功;否则就会失败。更重要的是,这一现象表明,即使有 step-by-step 的推理过程的帮助,transformers 也难以学会 rule-based reasoning —— 模型仍然在机械地记忆见过的单个步骤,而没有学会背后的规则。
其他影响因素
Scratchpad 以外,作者也在文章中对 test square 的位置、大小,模型的大小(包括 GPT-2-Medium,与更大的模型:Llama-2-7B 和 GPT-3.5-Turbo),数据集的大小等因素进行了丰富的测试。模型在做 case-based reasoning 的结论是统一的。具体的实验细节可见文章。
Rule-Following Fine-Tuning (RFFT)
通过上述的干预实验,作者发现 transformers 在数学推理中倾向于使用 case-based reasoning,然而,case-based reasoning 会极大地限制模型的泛化能力,因为这意味着模型如果要做对新的 test sample ,就需要在训练集中见过相似的样本。而在训练集中覆盖到所有未知推理问题的相似样本是几乎不可能的(尤其对于存在长度泛化的问题)。
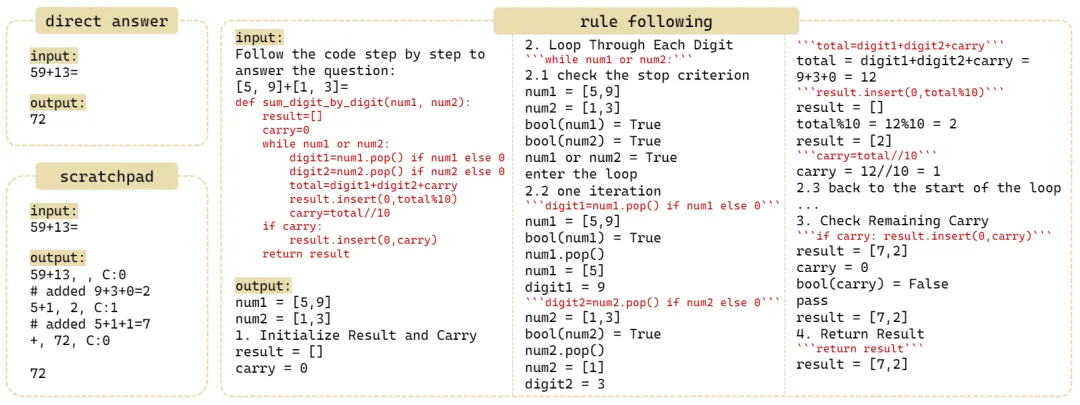
图 4:direct answer,scratchpad 与 rule-following 三种方法的 input-output sequence
为了缓解此类问题,作者提出了名为 Rule-Following Fine-Tuning(RFFT)的规则遵循微调技术,旨在教 transformers 进行 rule-based reasoning。具体来说,如图 4 所示,RFFT 在输入中提供显式的规则,然后指导 transformers 逐行地回忆规则并执行。
实验中,作者在 1-5 位数的加法上使用图 4 所示的三种方法对 Llama-2-7B 和 GPT-3.5-turbo 进行了 fine-tune,并分别在 6-9 与 6-15 位数的 OOD 的加法任务上进行了测试。
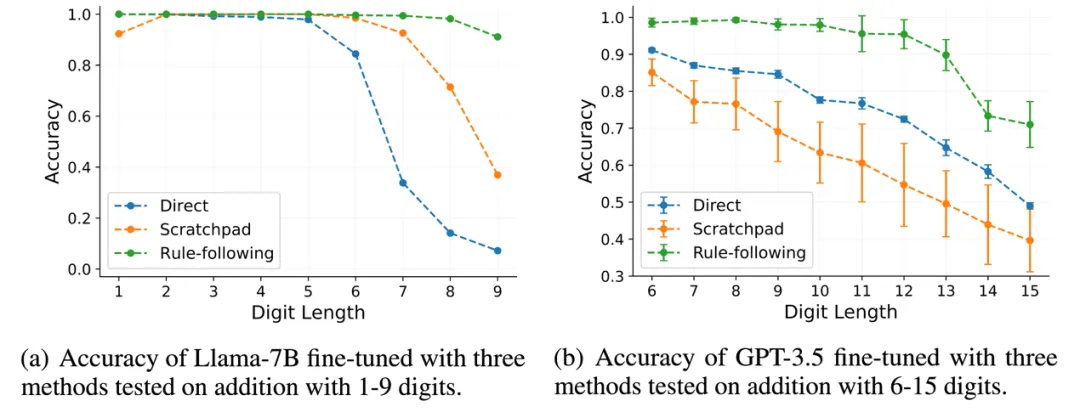
图 5:Llama-2-7b 和 GPT-3.5-turbo
由图 5 可见,RFFT 在长度泛化的性能上明显超过了 direct answer 和 scratchpad 这两种微调方法。使用 Llama-2-7B 进行 RFFT 时,模型在 9 位数的加法中也能保持 91.1% 的准确率。相比之下,使用 scratchpad 进行 fine-tune 的模型在此任务中的准确率不到 40%。对于拥有更强的基础能力的 GPT-3.5-turbo,RFFT 使其能够惊人地泛化到涉及多达 12 位数字的加法,尽管只在 1-5 位加法上训练了 100 个训练样本,但其在 12 位数的加法上仍然保持了 95% 以上的准确率。这也显著超过了 scratchpad 和 direct answer 的结果。这些结果突出显示了 RFFT 在引导 transformers 进行 rule-based reasoning 方面的有效性,并展现了其在增强模型长度泛化能力方面的潜力。
值得注意的是,作者发现 Llama-2-7B 需要 150,000 个训练样本才能泛化到 9 位数字,而 GPT-3.5 仅用 100 个训练样本就能掌握规则并泛化到 12 位数字。因此,规则遵循(rule-following)可能是一种 meta learning ability—— 它可能通过在多样化的 rule-following 数据上进行训练而得到加强,并可更容易地迁移到新的未在训练集中见过的领域中。相应地,基础模型越强大,理解并学习新的规则就越容易。这也与人类学习新规则的能力相符 —— 经验丰富的学习者通常学习得更快。
总结
本文探究了 transformers 在做数学推理问题时究竟是采用 case-based reasoning 还是 rule-based reasoning,并提出了 Rule-Following Fine-Tuning 的规则遵循微调方法来显式地教会 transformers 进行 rule-based reasoning。RFFT 展现了强大的长度泛化能力,并有潜力全面提升 LLMs 的推理能力。