当今 AI 领域爆火的大语言模型(LLM),其原理是香农提出来的?
今天,普林斯顿大学教授承现峻(Sebastian Seung)抛出了这样一个观点:1951 年,在贝尔实验室(总部位于新泽西州 Murray Hill)工作的克劳德・香农提出了预测下一个单词的问题,这成为了当前大语言模型(LLM)的种子。
如今很多看似新潮前沿的概念,其实距离提出已经相隔了好几十年,即使在计算机科学这样的新兴领域,例子也屡见不鲜。这个观点以及提到的 Murray Hill 引起热议,图灵奖得主、Meta 首席科学家 LeCun 表示,新泽西州的 Murray Hill、Florham Park 和普林斯顿都「诞生」了很多有影响力的工作。
LeCun 又列举了很多知名的研究成果:
- Hopfield 网络(美国科学家 Hopfield 同时在贝尔实验室和普林斯顿大学任职)。
- ConvNets
- Boosting/Adaboost
- 非负矩阵分解
- 支持向量机(SVM)和核机
- 结构化预测
- 计算学习理论 / VC 理论中的大量内容

那么说在这其中,香农给如今通向 AGI 的大模型起了个头,是怎么一回事呢?
讨论中提到的 IT 祖师爷克劳德・香农的论文是《Prediction and Entropy of Printed English》。

论文链接:https://www.princeton.edu/~wbialek/rome/refs/shannon_51.pdf
该研究于 1951 年 1 月发表在期刊《The Bell System Technical Journal》上,至今已被各路学者引用过超过 4000 次。
这篇论文中,香农主要探讨了如何估算语言的熵(entropy)和冗余度(redundancy),并提出了一种新方法。
其中:
- 语言的熵是衡量每个字母平均产生的信息量的统计参数。如果语言被最有效地转换成二进制数字(0 或 1),熵表示每个字母平均需要的二进制数字数量。
- 冗余度则衡量由于语言的统计结构(如字母频率、特定字母的后续趋势等)对文本施加的约束。
在定义了熵和冗余之后,就可以考虑把这些概念应用一下了。香农在他的论文中给出了两种估计英语熵的方法。冗余,或对英语文本施加的约束数量,导致其整体熵的下降。例如,规则「i before e except after c」,以及 q 必须始终跟 u 的事实是使英语更加冗余的依赖关系。语法规则、词性以及我们无法编造单词的事实也使英语变得有冗余。
英语中的冗余有时实际上是有益的,因为否则人们如何辨别在嘈杂的房间里说了什么?冗余允许人们在只有部分信息传来时推断出所说的内容。例如,如果听到「Turn phat mufic down!」,人们可以相当好地猜测说话者的意思。
计算英语熵的一种可能方法是使用 N-gram。
给定自然语言 L 的足够长的字符序列 S,考察所有长度为 N 的子字符串
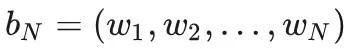
定义 N-gram 熵(Entropy)FN 如下。
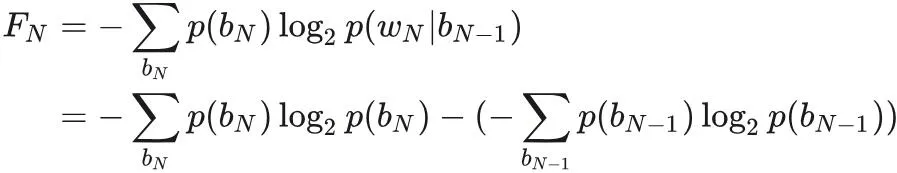
当已知前 N - 1 个字母时,我们可以统计计算出下一个字母的熵。随着 N 的增加,熵接近 H,此即英语的熵。以下是香农论文中计算出的值。FN 是当已知前 N - 1 个字母时与第 N 个字母相关的熵。计算 FN 统计数据的难度是 O (26^N),因为有那么多 N 个字母的序列。请注意,F0 只是字母集的最大熵,其中每个字母都有相等的概率。

27 个字母的序列,空格也算作一个字母。几乎总是可以从没有空格的单词序列中填充空格。因此空格基本上被视为是多余的,如果考虑空格,会导致计算出的熵值较低。只有在没有考虑统计数据的情况下,即 F0,添加空格后熵才会更高。这只是增加了另一个可能的符号,就意味着更多的不确定性。
香农建议的另一种策略是计算与英语中每个单词相关的熵,然后取加权平均值。香农使用近似函数来估计超过 8000 个单词的熵。他得到的每个单词的熵值为 11.82 bit,由于平均每个单词有 4.5 个字母,因此每个字母的熵为 2.62 bit。这在上表中以 Fword 给出。
我们已经讨论了如何从熵计算冗余度。当所有符号具有相同的可能性时,冗余度最大,等于 - (log2 (1/26)) = 4.7 bit / 字母。因此,使用公式 1 - H/Hmax,我们可以估算英语的冗余度。香农最初估计这个值为 50%,这意味着英语中大约一半的字母是多余的!
在同一篇文章的后面讨论了一种相当巧妙的计算英语熵的方法。它结合了英语的更多特征,例如统计方法无法明确解释的思路和上下文。
接下来就是如今我们在 NLP 中经常会提起的概念了:假设人类可以根据他们对该语言的先前了解来猜测单词或短语中的字母。香农的巧妙想法是利用这种自然的冗余度衡量标准…… 人类的思维。
他要求受试者逐个猜测短语中的字母。如果受试者猜对了,那么他 / 她就继续猜测下一个字母。如果不是,则告诉受试者下一个字母。在一个短语的 129 个字母中,69% 被猜对了。这意味着英语的冗余度大约为 69%。假设我们只重现那些猜错的字母,即 31%。那么我们可以通过复制从头开始猜测的受试者来恢复原始句子。受试者显然可以正确猜出 69% 的符号,并且他 / 她拥有其余的 31%,因此他 / 她可以仅使用大约 31% 的信息重现原始文本。
实际上,受试者需要的信息略多于 31%。他 / 她需要知道他 / 她会猜错的字母在哪里,因此实际上冗余度可能会少一点。从理论上讲,这是一个很好的例子,但实际上并非如此。句子和受试者的抽样误差会导致结果严重失真。尽管如此,这个例子有助于说明冗余的一个实际例子,并阐明了如何编码英语。无需创建英语的统计语法来计算其熵,人类天生就具有语法。
统计计算英语的冗余有许多实际应用。ASCII 每个字符保留 8 个二进制数字。然而,考虑到一些计算将英语的熵定为大约 1 位 / 字母,这是非常低效的。这意味着理论上存在一种压缩方案,其压缩效果是 ASCII 的 8 倍。现代计算机显然拥有足够大的内存,因此这种低效率并不重要,但 Huffman 压缩和 Lempel-Ziv 压缩算法在存储文本时可以节省大量空间。
通常,当人们说英语是冗余的时,他们指的是大量同义词使我们的词典变得杂乱。信息论意义上的冗余是衡量字母 / 符号在语言中使用效率的指标。英语是一种冗余语言,这不一定是坏事。我们的语言既可以口语也可以书写,除了效率之外,还带来了许多问题。我们希望在嘈杂的房间里也能被人听懂,我们希望单词的发音与含义相对应,我们希望能够轻松地发音。信息率只是英语分析的一小部分。
一个非常有趣的例子可以说明一种语言在统计上能有多好地描述,即英语的 n 阶近似,这是香农最著名的论文《A mathematical theory of communication》里所提到的。如果一只猴子知道英语中字母的 n-gram 频率(其中 n 很大),它能写出可信的英语文本吗?此外,这只猴子「懂」英语吗?如果 N-gram 猴子在一扇门后面,而人类在另一扇门后面,第三方观察者能分辨出哪个是猴子吗?这个问题让人想起了人工智能的图灵测试,它没有简单的答案。
但如今的大模型原理,正是通过学习大量的文本数据,来预测下一个词或下一段话的可能性,从而使计算机能够更好地「理解」和生成人类语言。

AI 理解了吗?不好说。但是能猜对吗?看看如今的 ChatGPT,人们心中都已经有了答案。
这也不禁令人感叹,香农真的领先于他的时代。