使用 Python 进行财务数据分析实战-51CTO.COM

在迅速变化的金融领域中，数据分析和解释的能力至关重要。本文探讨了Python在金融数据分析中的应用，包括使用Pandas、NumPy和Matplotlib等Python库，它们能够处理股票市场数据、展示趋势并构建交易策略。无论你是经验丰富的金融分析师还是初入投资领域者，这些见解和技巧都将增强你的分析技能，拓宽对金融市场动态的理解，并帮助你在股票市场做出明智的决策。

import pandas as pd
import numpy as np
import datetime
import matplotlib.pyplot as plt

以下代码使用 Python 中常用的库来处理数据，执行数值计算、日期时间操作和数据可视化。这些包括 pas、numpy、datetime、matplotlib.pyplot。Pas 提供强大的数据结构（例如 DataFrames）来组织分析数据，而 numpy 允许对数组进行有效的数学运算。datetime 模块允许涉及日期时间的操作计算，而 matplotlib.pyplot 可用于在 Python 中创建各种类型的可视化，尤其是数据的图表。

导入数据

from pandas_datareader import data as pdr
import yfinance

aapl = pdr.get_data_yahoo('AAPL', 
                          start=datetime.datetime(2006, 10, 1), 
                          end=datetime.datetime(2012, 1, 1))
aapl.head()

图片

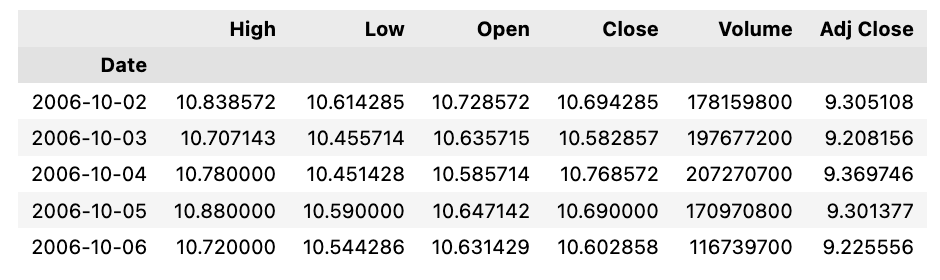
此代码使用 pas_datareader 从 Yahoo Finance 检索 Apple Inc. 的历史股价数据。它获取 2006 年 10 月至 2012 年 1 月的每日数据，显示数据框的前五行。这里使用yfinance 库用于访问 Yahoo Finance 的数据，没使用pas_datareader 的默认方法。

import quandl 
aapl = quandl.get("WIKI/AAPL", start_date="2006-10-01",
                  end_date="2012-01-01")
aapl.head()

图片

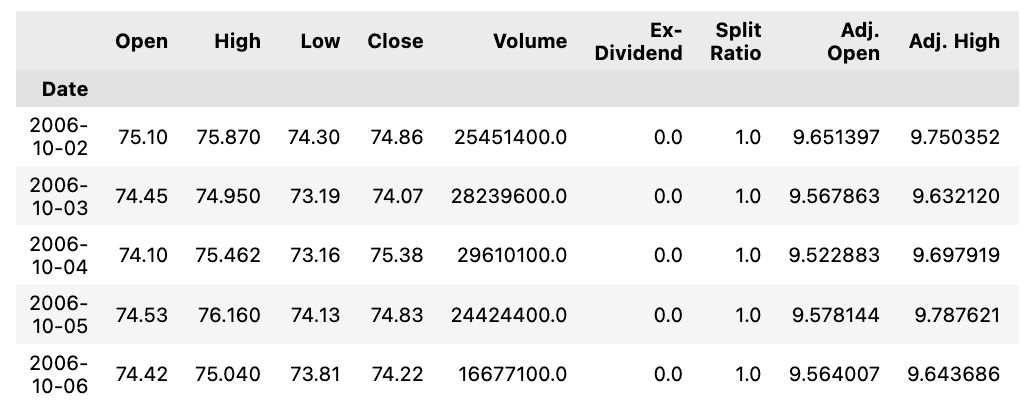
这里演示了如何使用 Qul 库从 WIKI 数据库中提取 Apple Inc. 的历史股票市场数据。数据涵盖 2006 年 10 月 1 日至 2012 年 1 月 1 日之间的日期。

使用时间序列数据

aapl.index
aapl.columns
ts = aapl['Close'][-10:]
type(ts)

图片

aapl 为 Apple Inc. 的股票市场数据。代码使用 aapl.index 选择索引，使用 aapl.columns 选择列名，其中包括'Open', 'Close', 'High', 'Low', 'Volume'（“开盘价”、“收盘价”、“最高价”、“最低价”、“成交量”）等字段。然后，它将“收盘价”列中的最后 10 个条目分配给变量 ts，并使用 type(ts) 确定其类型，该变量可能是 pandas Series 对象。请注意，代码缺少正确的标点符号语法，仅作为概念解释，而不是可执行代码的一部分。

aapl['diff'] = aapl.Open - aapl.Close
del aapl['diff']

这段代码创建一个名为“diff”的新列，该列表示“开盘价”和“收盘价”值之间的差异。填充此列后，它会立即从 DataFrame 中删除，保留其原始结构。

import matplotlib.pyplot as plt 
aapl['Close'].plot(grid= True ) 
plt.show()

图片

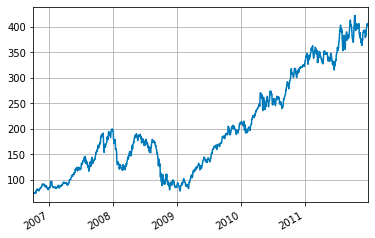
这里创建了一个显示 Apple Inc. 股票收盘价的图表。图表中添加了网格，有助于分析 AAPL 股价在一段时间内的模式。

daily_close = aapl[['Adj Close']]

daily_pct_c = daily_close.pct_change()

daily_pct_c.fillna(0, inplace=True)
print(daily_pct_c)

daily_log_returns = np.log(daily_close.pct_change()+1)
print(daily_log_returns)

图片

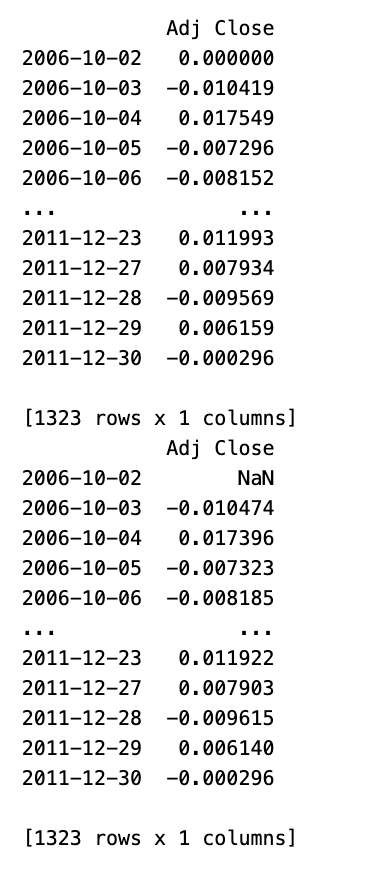
这段代码对苹果公司股票的财务数据进行了分析，特别关注了调整后的收盘价。首先选择了调整后的收盘价列，然后计算了每日的百分比变化，对任何缺失值用 0 进行了替换。接下来，将百分比变化数据框打印到控制台。另外，使用 np.log() 函数计算了每日的对数收益，并将结果数据框打印出来。这段代码提供了苹果股票每日收益的两个不同角度。

monthly = aapl.resample('BM').apply(lambda x: x[-1])
monthly.pct_change()
quarter = aapl.resample("4M").mean()
quarter.pct_change()

图片

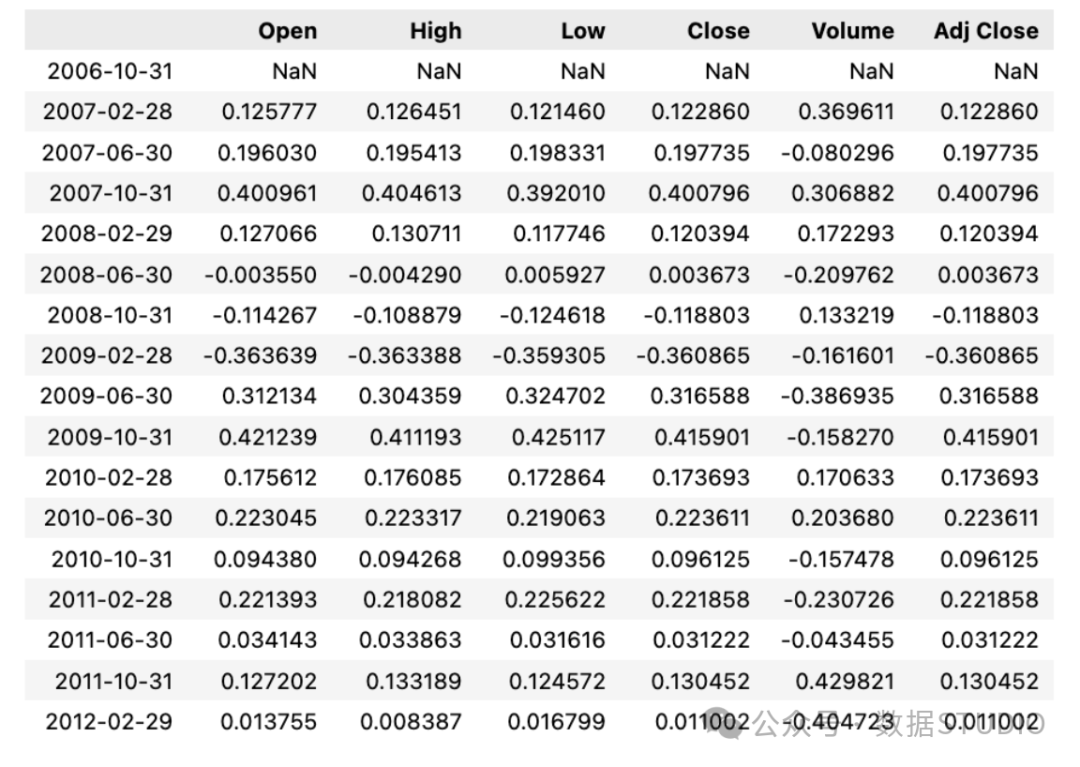
该代码处理了代表苹果公司（Apple Inc.）股票价格的变量aapl的时间序列数据。首先，对数据进行重新采样，以获取每个月的最后一个工作日，并使用lambda函数选择每个月的最后一个数据点，创建了名为monthly的新时间序列。然后，计算了每个月度数据点之间的百分比变化，以显示aapl的月度增长或下降。接下来，对原始时间序列重新采样，以计算四个月的平均值，创建了名为quarter的新时间序列。最后，计算了每个四个月期间的平均值之间的百分比变化，表示了每个四个月期间的比例增加或减少。需要进一步编写代码才能存储或输出这些计算结果。

import matplotlib.pyplot as plt
daily_pct_c.hist(bins=50)
plt.show()
print(daily_pct_c.describe())

图片

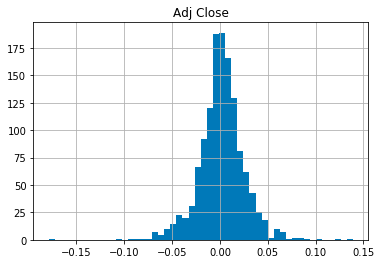
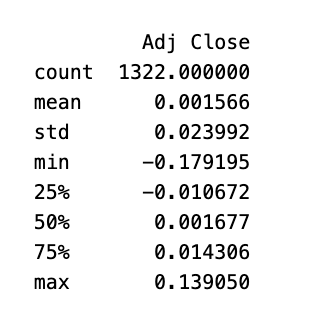
在 daily_pct_c 表示的数据集上调用 hist() 方法，创建一个具有 50 个间隔的直方图。然后使用 plt.show() 显示直方图。最后，使用 describe() 方法打印数据集的描述性统计数据，从而深入了解其分布情况。

cum_daily_return = (1 + daily_pct_c).cumprod()

print(cum_daily_return)

图片

import matplotlib.pyplot as plt 

cum_daily_return.plot(figsize=(12,8))

plt.show()

图片

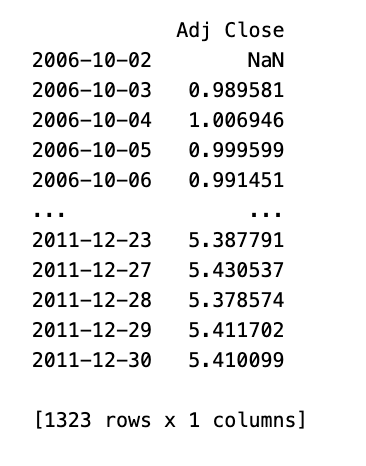
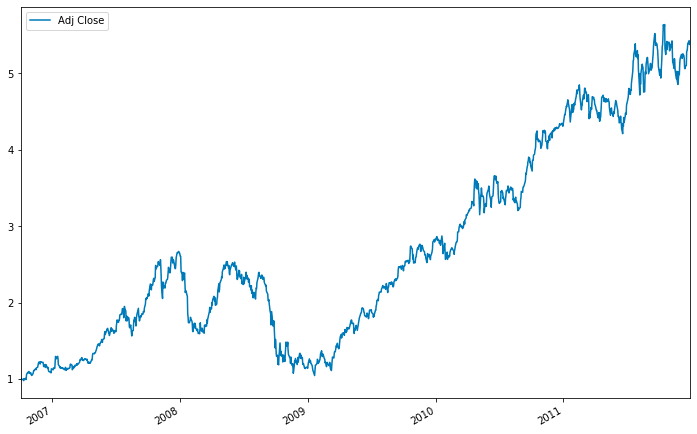
可见的代码段使用了 matplotlib 库来实现数据可视化。它调用了名为 cum_daily_return 的 Pandas DataFrame 或 Series 上的 plot 方法，用于生成累积每日收益图。图形的尺寸被设定为 12 x 8 英寸，并使用 plt.show() 来显示图形。需要注意代码中可能存在缺失部分。

cum_monthly_return = cum_daily_return.resample("M").mean()

print(cum_monthly_return)

图片

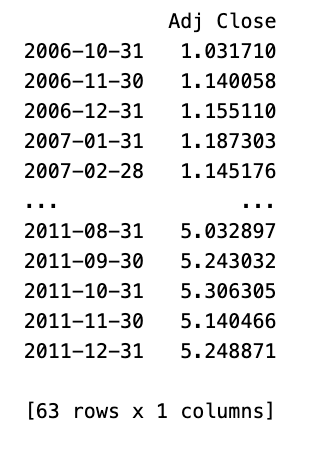
代码从财务数据集中提取每日累计收益，并将其重新采样以计算每月的平均累计收益。在重新采样过程中，每日收益的频率被更改为每月，并计算每个月的平均每日收益。最终结果将打印出每月平均收益。

from pandas_datareader import data as pdr
import yfinance

def get(tickers, startdate, enddate):
    def data(ticker):
        return (pdr.get_data_yahoo(ticker, start=startdate, end=enddate))
    datas = map(data, tickers)
    return(pd.concat(datas, keys=tickers, names=['Ticker', 'Date']))

tickers = ['AAPL', 'MSFT', 'IBM', 'GOOG']
all_data = get(tickers, datetime.datetime(2006, 10, 1), datetime.datetime(2012, 1, 1))
all_data.head()

图片

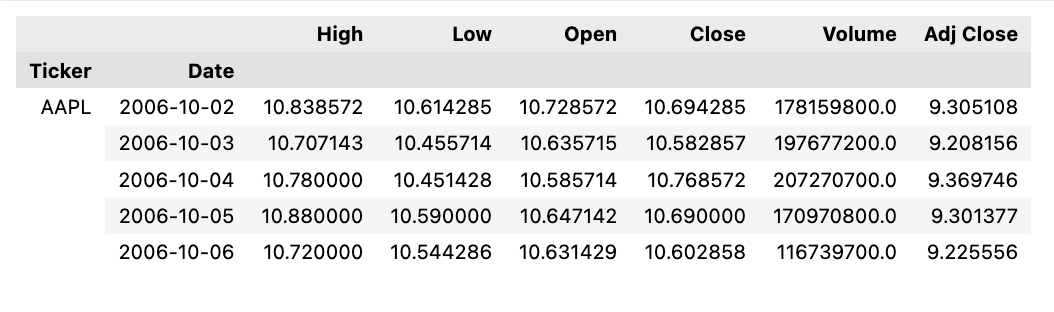
使用了pas_datareader库中的yfinance作为数据源从 Yahoo Finance 获取股票代码列表的历史财务数据。该函数需要股票代码列表、开始和结束日期作为参数，并使用子函数data检索每个股票代码的数据。

接下来，函数map将应用于每个股票代码，将生成的数据组合成具有分层索引的单个 DataFrame。此外，还提供了该函数的示例用法，其中获取了四家科技公司的数据，并显示了组合数据集的前几行。

daily_close_px = all_data[['Adj Close']].reset_index().pivot('Date', 'Ticker', 'Adj Close')

daily_pct_change = daily_close_px.pct_change()

daily_pct_change.hist(bins=50, sharex=True, figsize=(12,8))

plt.show()

图片

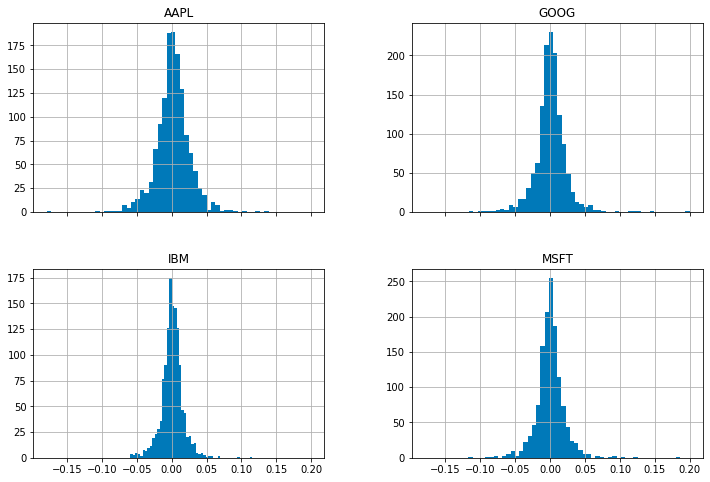
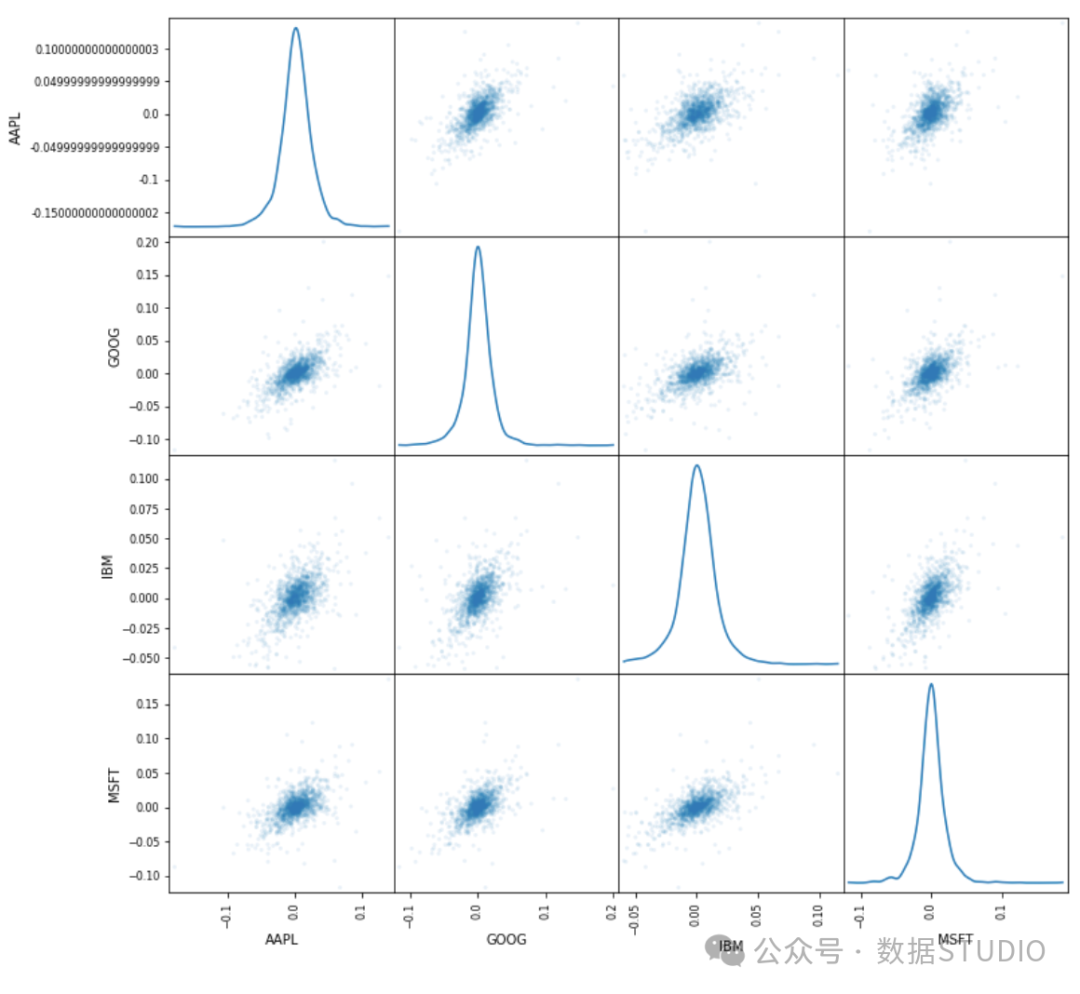
通过分析财务数据，我们使用股票调整后收盘价的每日百分比变化计算，并将结果呈现在一个直方图中。

首先，我们从包含股票市场数据的名为 all_data 中选择Adj Close列，该列反映了考虑股息股票分割等因素后股票的调整后收盘价。
然后，我们重置指数数据，以便每行代表一个日期，每列代表一个股票代码。
接着，我们使用 pct_change() 方法计算股票价格的每日百分比变化，并将其呈现在一个有 50 个箱的直方图中。这些直方图共享相同的 x 轴，大小为 12x8 英寸，便于进行比较。

这段代码有效地总结了给定数据集中调整后收盘价的每日百分比变化分布。

pd.plotting.scatter_matrix(daily_pct_change, diagnotallow='kde', alpha=0.1,figsize=(12,12))

plt.show()

图片

此代码为 daily_pct_change 数据集创建散点图矩阵。每个单元格显示两个变量的散点图，对角线图显示 KDE 图以可视化单个变量的分布。点的透明度值为 0.1 以显示密度，图形大小设置为 12 x 12 英寸。

adj_close_px = aapl['Adj Close'] 

moving_avg = adj_close_px.rolling(window=40).mean() 

moving_avg[-10:]

图片

代码对 Apple Inc. (AAPL) 的财务数据进行了处理。它使用了名为“aapl”的数据集，并选择了其中的“调整后的收盘价”，这代表了股票分割和红利调整后的收盘价。接着，它计算了这些价格的 40 周期移动平均值。最后，它提取了移动平均线的最后 10 个值，以观察股票价格近期趋势的变化。移动平均线有助于平滑短期波动，并凸显长期趋势。

aapl['42'] = adj_close_px.rolling( window = 40 ).mean() 
aapl['252'] = adj_close_px.rolling( window = 252 ).mean() 
aapl[['Adj Close', '42', '252']].plot() 
plt. show ()

图片

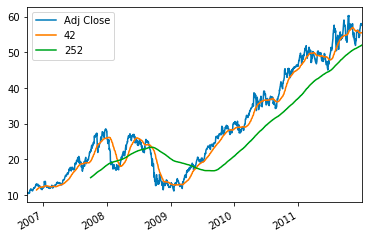
以下代码对财务数据（特别是 Apple Inc. (AAPL) 的股票价格）进行操作。这包括计算调整后的收盘价的 40 天移动平均线和 252 天移动平均线，然后将其存储在aapl 的“42”和“252”列中。然后使用这些移动平均线和调整后的收盘价生成图表，以直观的方式分析随时间变化的股价趋势。

min_periods = 75 

vol = daily_pct_change.rolling(min_periods).std() * np.sqrt(min_periods) 
vol.plot(figsize=(10, 8))
plt.show()

图片

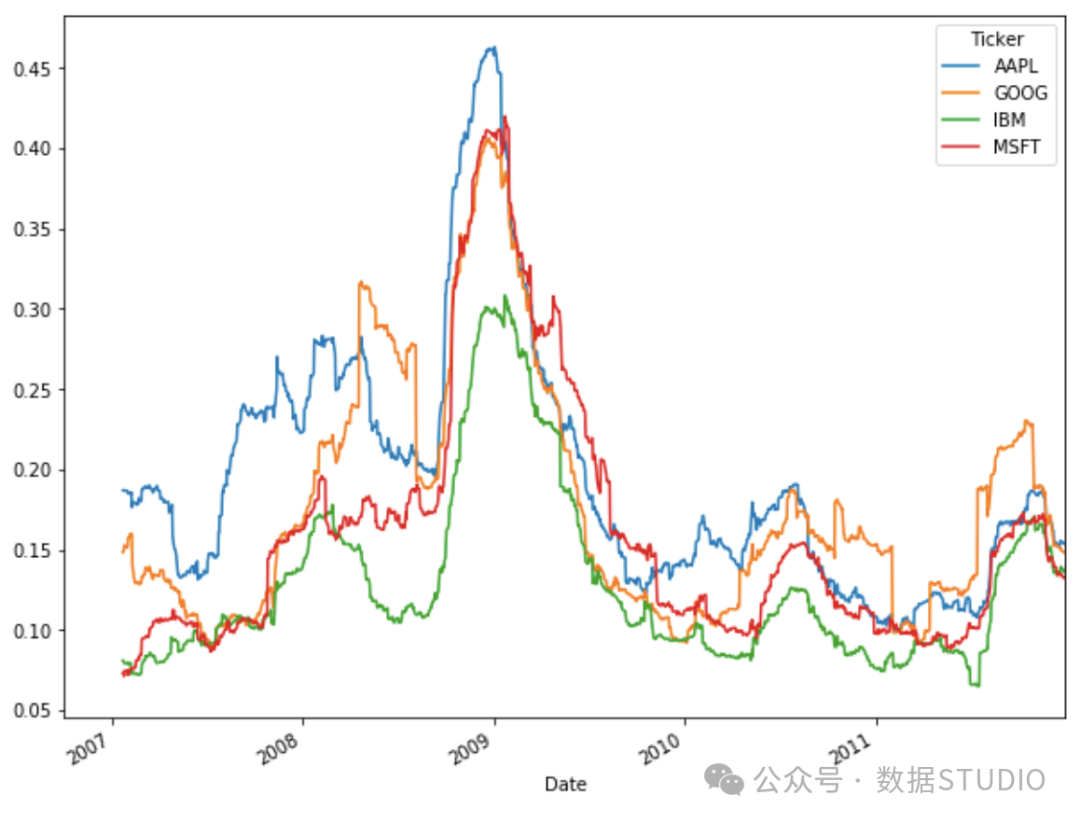
这里根据金融资产的每日价格百分比变化计算其滚动波动率。它使用变量 min_periods 表示一年的一个季度，以此作为窗口大小计算滚动标准差。然后将得到的测量值乘以 min_periods 的平方根，将其年化。这段代码将每日价格变化的百分比用于计算资产的滚动波动率。过程包括设定 min_periods 变量表示一年的一个季度，计算滚动标准差，然后将结果乘以 min_periods 的平方根，实现年化计算。

import statsmodels.api as sm
import pandas
from pandas import tseries

all_adj_close = all_data[['Adj Close']]

all_returns = np.log(all_adj_close / all_adj_close.shift(1))

aapl_returns = all_returns.iloc[all_returns.index.get_level_values('Ticker') == 'AAPL']
aapl_returns.index = aapl_returns.index.droplevel('Ticker')

msft_returns = all_returns.iloc[all_returns.index.get_level_values('Ticker') == 'MSFT']
msft_returns.index = msft_returns.index.droplevel('Ticker')

return_data = pd.concat([aapl_returns, msft_returns], axis=1)[1:]
return_data.columns = ['AAPL', 'MSFT']

X = sm.add_constant(return_data['AAPL'])

model = sm.OLS(return_data['MSFT'],X).fit()

print(model.summary())

图片

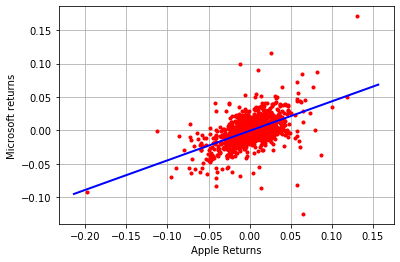
此代码使用股票数据集来分析苹果公司和微软公司的股票收益之间的关系。它计算对数收益，使用普通最小二乘法创建线性回归模型。然后拟合模型并输出摘要，深入了解两只股票收益之间的关系。

plt.plot(return_data['AAPL'], return_data['MSFT'], 'r.')

ax = plt.axis()
x = np.linspace(ax[0], ax[1] + 0.01)

plt.plot(x, model.params[0] + model.params[1] * x, 'b', lw=2)

plt.grid(True)
plt.axis('tight')
plt.xlabel('Apple Returns')
plt.ylabel('Microsoft returns')

plt.show()

图片

在这里创建散点图和线图。散点图使用红点比较“AAPL”和“MSFT”的收益，而直线图则显示基于“AAPL”收益的模型预测。该代码直观地显示了 Apple 和 Microsoft 股票收益之间的关系，包括模型的预测。

return_data['MSFT'].rolling(window=252).corr(return_data['AAPL']).plot()
plt.show()

图片

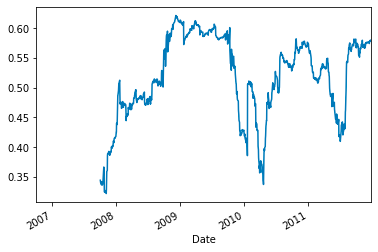
该代码通过计算 Apple 和 Microsoft 股票 252 天每日收益之间的滚动相关性来分析财务数据。然后将此相关性显示在图表上，以直观地展示两只股票之间随时间变化的相关性。

使用 Python 构建交易策略

short_window = 40
long_window = 100

signals = pd.DataFrame(index=aapl.index)
signals['signal'] = 0.0

signals['short_mavg'] = aapl['Close'].rolling(window=short_window, min_periods=1, center=False).mean()

signals['long_mavg'] = aapl['Close'].rolling(window=long_window, min_periods=1, center=False).mean()

signals['signal'][short_window:] = np.where(signals['short_mavg'][short_window:] 
                                            > signals['long_mavg'][short_window:], 1.0, 0.0)   

signals['positions'] = signals['signal'].diff()

这段代码利用了Apple Inc.股票的收盘价移动平均线来生成交易信号。

首先设置了两个变量，分别代表短期和长期移动平均线的长度。
接下来，初始化一个DataFrame来包含信号，其中一列表示信号，另一列表示位置。代码会计算并将短期和长期移动平均线加入到信号DataFrame的各自列中。
最后，通过比较这两个移动平均线来生成交易信号，如果短期大于长期，就将信号列设为1.0。而位置列则用来捕获信号的变化，并在生成新信号时显示。

总的来说，这段代码实现了一个简单的移动平均线交叉策略，用于交易苹果股票。

fig = plt.figure()

ax1 = fig.add_subplot(111,  ylabel='Price in $')

aapl['Close'].plot(ax=ax1, color='r', lw=2.)

signals[['short_mavg', 'long_mavg']].plot(ax=ax1, lw=2.)

ax1.plot(signals.loc[signals.positions == 1.0].index, 
         signals.short_mavg[signals.positions == 1.0],
         '^', markersize=10, color='m')
         
ax1.plot(signals.loc[signals.positions == -1.0].index, 
         signals.short_mavg[signals.positions == -1.0],
         'v', markersize=10, color='k')
         
plt.show()

图片

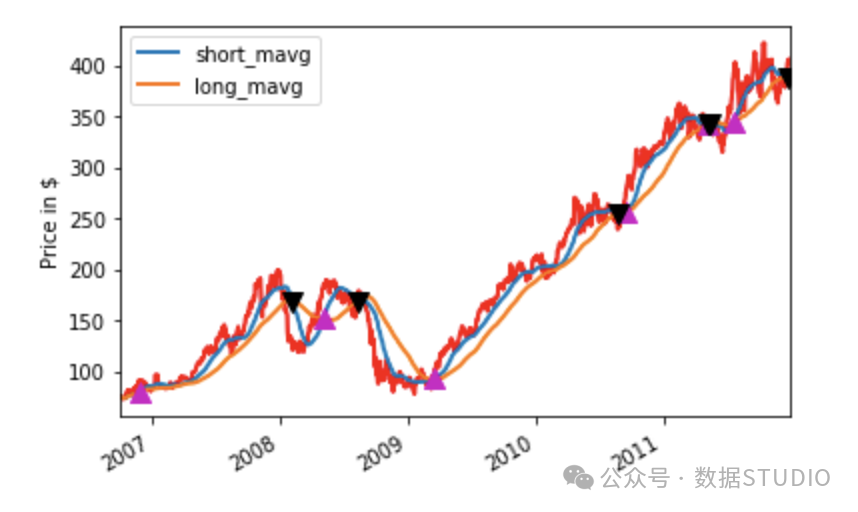
段代码用于绘制财务图表。首先需要初始化一个图形，然后添加一个子图，其中包含股票价格标签。在子图中，使用红色绘制苹果公司股票的收盘价，并加入两条移动平均线。在买入信号处添加符号^，在卖出信号处添加符号v，这两个符号均位于短移动平均线的顶部。最终的图表将显示在窗口中。信号变量包含交易信号、短长移动平均线以及图表上标记的买入/卖出。

回测策略

回测策略是指通过历史数据来验证交易策略的有效性和盈利性。通常进行回测策略需要以下步骤：

选择历史数据：从可靠的数据源获取需要的历史数据，包括价格数据、成交量等。
编写交易策略：根据自己的投资理念和市场分析，编写一个可执行的交易策略，包括买入、卖出和止损条件等。
运行回测程序：使用专业的回测软件或编程语言，将交易策略应用到历史数据上，模拟交易执行过程，记录交易成绩和盈亏。
优化策略：根据回测结果，对交易策略进行优化，比如调整参数、修改条件等，以提高策略的有效性和盈利性。
验证和执行：经过反复的回测和优化，最终验证交易策略的稳健性和盈利性，然后可以开始执行该策略进行实盘交易。

initial_capital= float(100000.0)
positions = pd.DataFrame(index=signals.index).fillna(0.0)
positions['AAPL'] = 100*signals['signal']   
portfolio = positions.multiply(aapl['Adj Close'], axis=0)
pos_diff = positions.diff()
portfolio['holdings'] = (positions.multiply(aapl['Adj Close'], axis=0)).sum(axis=1)
portfolio['cash'] = initial_capital - (pos_diff.multiply(aapl['Adj Close'], axis=0)).sum(axis=1).cumsum()   
portfolio['total'] = portfolio['cash'] + portfolio['holdings']
portfolio['returns'] = portfolio['total'].pct_change()

此代码用于股票交易回测策略中的财务分析。它首先设置初始投资金额 100,000 美元，创建一个名为“positions”的数据框来表示持有的股票“AAPL”的股份数量。股份数量通过将买入或卖出信号乘以 100 来计算，创建一个名为“portfolio”的新数据框来计算“AAPL”股份的市场价值。该代码还计算头寸差异，更新“持股”和“现金”列，计算投资组合在一段时间内的总回报。本质上，该代码根据给定的信号模拟“AAPL”的股票交易。

import matplotlib.pyplot as plt

fig = plt.figure()

ax1 = fig.add_subplot(111, ylabel='Portfolio value in $')

portfolio['total'].plot(ax=ax1, lw=2.)

ax1.plot(portfolio.loc[signals.positions == 1.0].index, 
         portfolio.total[signals.positions == 1.0],
         '^', markersize=10, color='m')

ax1.plot(portfolio.loc[signals.positions == -1.0].index, 
         portfolio.total[signals.positions == -1.0],
         'v', markersize=10, color='k')

plt.show()

图片

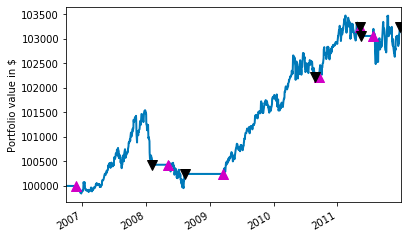
此代码实现财务数据可视化。制作了一个新图形，其子图包含一组标记为投资组合价值（以美元计）的轴，以显示投资组合总价值随时间的变化。折线图的线宽为 2，买入卖出信号分别用洋红色黑色三角形表示，大小为 10。

评估移动平均线交叉策略

returns = portfolio['returns']

sharpe_ratio = np.sqrt(252) * (returns.mean() / returns.std())

print(sharpe_ratio)

下面的代码用于计算金融投资组合的夏普比率（Sharpe Ratio）。这个比率用于衡量投资相对于无风险资产的表现，并根据投资的风险进行调整。以下是代码执行的步骤：

从包含财务数据的投资组合变量中提取“回报”系列。
通过对每日平均收益进行标准化，使用标准差来计算夏普比率，以确定风险调整后的收益。
夏普比率的年化值是将其乘以 252 的平方根，代表一年中的典型交易日数。
打印出由此得出的夏普比率，以便投资者了解持有高风险资产所承受的额外风险所带来的超额回报。夏普比率越高，风险调整后的回报就越有利。

夏普比率（Sharpe Ratio）是一种用于衡量投资组合风险调整后收益的指标，它是由诺贝尔经济学奖获得者威廉·夏普（William Sharpe）于1966年提出的。

夏普比率通过比较投资组合的超额收益与其相对于无风险利率的标准偏差之比来衡量投资组合的风险调整后收益。夏普比率的计算公式为：

夏普比率 = （投资组合年化收益率 - 无风险利率） / 投资组合年化波动率

其中，投资组合年化收益率是指投资组合在一段时间内的平均收益率，无风险利率是指没有风险的投资的利率（通常取国债利率），投资组合年化波动率则是投资组合收益率的标准差。

夏普比率的数值越高，表示投资组合单位风险所获得的超额收益越高，因此夏普比率可以用来度量投资组合的风险调整后表现。通常情况下，夏普比率越高，投资组合的绩效越好。

最大回撤

最大回撤是指在一段时间内资产价格从最高点下跌的幅度。通常用来衡量风险和资产价格波动的程度。最大回撤可以帮助投资者评估投资组合的风险水平，以及资产的价格波动性。在量化投资中，最大回撤也是一个重要的指标，用来评估交易策略的风险和表现。

window = 252

rolling_max = aapl['Adj Close'].rolling(window, min_periods=1).max()
daily_drawdown = aapl['Adj Close']/rolling_max - 1.0

max_daily_drawdown = daily_drawdown.rolling(window, min_periods=1).min()

daily_drawdown.plot()
max_daily_drawdown.plot()

plt.show()

图片

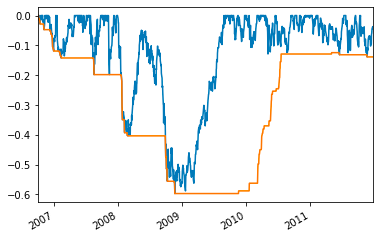
该步骤旨在分析苹果公司（代码：AAPL）股票的财务数据。它通过计算252天窗口内的滚动最高调整收盘价，以确定从该最高价到当前价格的每日跌幅（以百分比表示）。该代码还计算了同一时期的最大每日跌幅，这代表了从峰值下降的最大百分比。然后，将这些值绘制在图表上，以直观显示在选定期限内持有AAPL股票的潜在风险。