通透！机器学习中常用的几种距离度量方法-51CTO.COM

大家好，我是小寒。

今天给大家分享机器学习中经常使用的不同类型的距离度量。

在机器学习中，距离度量是一种用于计算两个数据点之间相似性或差异性的方法。它在许多算法中起着至关重要的作用，尤其是在无监督学习（如聚类）和监督学习（如最近邻分类）中。

向量距离测量

让我们首先了解机器学习中使用的不同向量距离测量。

1.欧几里得距离

欧几里得距离是最常见的距离度量，用于计算两个点在 n 维空间中的直线距离。

import numpy as np

def euclidean_distance(x, y):
    return np.sqrt(np.sum((np.array(x) - np.array(y))**2))

# 示例
x = [1, 2, 3]
y = [4, 5, 6]
print(euclidean_distance(x, y))  # 输出：5.196152422706632

2.曼哈顿距离

曼哈顿距离计算两个点之间的绝对坐标差的总和，适用于在规则网格上测量距离的情况，例如城市街道、棋盘格等。

曼哈顿距离的公式为

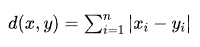
其中， x 和 y 是 n 维空间中的两个点，

def manhattan_distance(x, y):
    return sum(abs(a - b) for a, b in zip(x, y))

# 示例
x = [1, 2]
y = [4, 6]
print(manhattan_distance(x, y))  # 输出：7

3.明科夫斯基距离

明科夫斯基距离是欧几里得距离和曼哈顿距离的广义形式，取决于参数 p 的值。

当 p 为 1时，为曼哈顿距离；当 p 为 2时，为欧几里得距离；当 p 为无穷大时，为切比雪夫距离。

def minkowski_distance(x, y, p=2):
    return np.sum(np.abs(np.array(x) - np.array(y))**p)**(1/p)

# 示例
x = [1, 2, 3]
y = [4, 5, 6]
print(minkowski_distance(x, y, p=3))  # 输出：4.3267487109222245

统计相似性

1.余弦相似度

余弦相似度是通过计算两个向量之间的余弦角度来度量它们的相似性。

余弦相似度的值介于 -1 和 1 之间，1 表示完全相似，-1 表示完全不相似。

import numpy as np

def cosine_similarity(A, B):
    dot_product = np.dot(A, B)
    norm_A = np.linalg.norm(A)
    norm_B = np.linalg.norm(B)
    return dot_product / (norm_A * norm_B)

# 示例向量
A = np.array([1, 2, 3])
B = np.array([4, 5, 6])

# 计算余弦相似度
similarity = cosine_similarity(A, B)
print("余弦相似度:", similarity)

2.皮尔逊相关系数

皮尔逊相关系数衡量的是两个变量之间的线性相关性，取值范围为 -1 到 1。

1 表示完全正相关，-1 表示完全负相关，0 表示无相关性。

import numpy as np

def pearson_correlation(A, B):
    mean_A = np.mean(A)
    mean_B = np.mean(B)
    numerator = np.sum((A - mean_A) * (B - mean_B))
    denominator = np.sqrt(np.sum((A - mean_A)**2)) * np.sqrt(np.sum((B - mean_B)**2))
    return numerator / denominator

# 示例向量
A = np.array([1, 2, 3, 4, 5])
B = np.array([5, 4, 3, 2, 1])

# 计算皮尔逊相关系数
correlation = pearson_correlation(A, B)
print("皮尔逊相关系数:", correlation)

3.杰卡德指数

杰卡德指数（Jaccard Index），又称杰卡德相似系数（Jaccard Similarity Coefficient），是一种用于衡量两个集合之间相似度的统计指标。

它通过计算两个集合的交集和并集的比率来衡量它们的相似性。

def jaccard_index(set1, set2):
    intersection = len(set(set1).intersection(set(set2)))
    union = len(set(set1).union(set(set2)))
    return intersection / union

# 示例数据
set1 = {1, 2, 3}
set2 = {2, 3, 4}

print(jaccard_index(set1, set2))  # 输出：0.5

基于编辑的距离测量

1.汉明距离

它测量两个等长字符串之间不同字符的数量。

def hamming_distance(x, y):
    if len(x) != len(y):
        raise ValueError("Strings must be of the same length")
    return sum(el1 != el2 for el1, el2 in zip(x, y))

# 示例
x = '1011101'
y = '1001001'
print(hamming_distance(x, y))

2.编辑距离

它根据将一个字符串转换为另一个字符串需要多少次更正来计算。允许的更正包括插入、删除和替换。

def edit_distance(s1, s2):
    m, n = len(s1), len(s2)
    dp = [[0] * (n + 1) for _ in range(m + 1)]
    
    for i in range(m + 1):
        for j in range(n + 1):
            if i == 0:
                dp[i][j] = j
            elif j == 0:
                dp[i][j] = i
            elif s1[i - 1] == s2[j - 1]:
                dp[i][j] = dp[i - 1][j - 1]
            else:
                dp[i][j] = 1 + min(dp[i][j - 1], dp[i - 1][j], dp[i - 1][j - 1])
    
    return dp[m][n]

# 示例
s1 = "kitten"
s2 = "sitting"
print(edit_distance(s1, s2))