本文作者曾秋皓，加拿大西安大略大学计算机系博士研究生，本科毕业于哈尔滨工业大学，硕士毕业于新加坡国立大学。在王博予教授和凌晓峰院士的指导下，博士期间主要围绕随时间变化的分布的问题展开理论、方法和应用的研究。目前已在 ICLR/AAAI/IEEE TNNLS 发表多篇学术论文。
个人主页：https://hardworkingpearl.github.io/
在现实世界的机器学习应用中，随时间变化的分布偏移是常见的问题。这种情况被构建为时变域泛化（EDG），目标是通过学习跨领域的潜在演变模式，并利用这些模式，使模型能够在时间变化系统中对未见目标域进行良好的泛化。然而，由于 EDG 数据集中时间戳的数量有限，现有方法在捕获演变动态和避免对稀疏时间戳的过拟合方面遇到了挑战，这限制了它们对新任务的泛化和适应性。
为了解决这个问题，我们提出了一种新的方法 SDE-EDG，它通过连续插值样本收集数据分布的无限细分网格演变轨迹（IFGET），以克服过拟合的问题。此外，通过利用随机微分方程（SDEs）捕获连续轨迹的固有能力，我们提出了将 SDE 建模的轨迹通过最大似然估计与 IFGET 的轨迹对齐，从而实现捕获分布演变趋势。
- 论文标题：Latent Trajectory Learning for Limited Timestamps under Distribution Shift over Time
- 论文链接：https://openreview.net/pdf?id=bTMMNT7IdW
- 项目链接：https://github.com/HardworkingPearl/SDE-EDG-iclr2024
方法
核心思想
为了克服这一挑战，SDE-EDG 提出了一种新颖的方法，通过构建无限细分网格演变轨迹（Infinitely Fined-Grid Evolving Trajectory, IFGET），在潜在表示空间中创建连续插值样本，以弥合时间戳之间的间隔。此外，SDE-EDG 利用随机微分方程（Stochastic Differential Equations, SDEs）的内在能力来捕捉连续的轨迹动态，通过路径对齐正则化器将 SDE 建模的轨迹与 IFGET 对齐，从而实现跨域捕获演变分布趋势。
方法细节
1. 构建 IFGET：
首先，SDE-EDG 在潜在表示空间中为每个样本建立样本到样本的对应关系，收集每个个体样本的演变轨迹。对于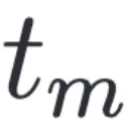
时刻的每个类别 k 的任一样本
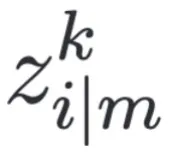，我们搜索
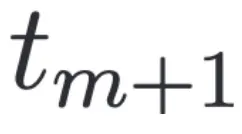时刻在特征空间离其最近的
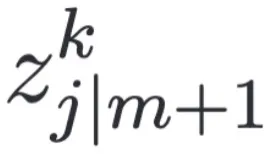为其在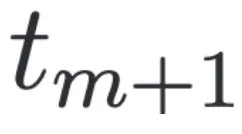
的对应样本：
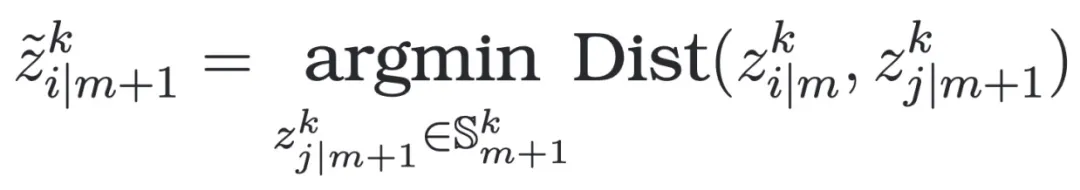
这里
是计算两个向量之间的距离，
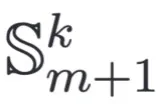是从下个领域
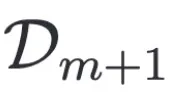采样的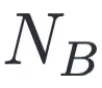
个样本的集合。
然后，利用这种对应关系生成连续插值样本，旨在连接时间戳间隔之间的时间间隙，避免对稀疏时间戳的过拟合，
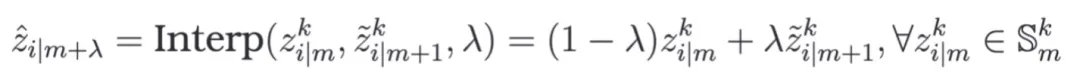
这里
采样自 Beta 分布。通过收集通过以上方式产生的样本的时序轨迹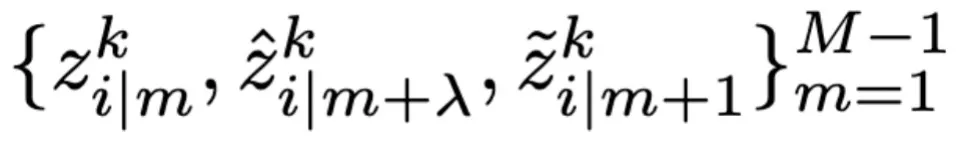
，我们得到 IFGET。
2. 使用 SDE 建模轨迹：
SDE-EDG 采用神经 SDE 来模拟数据在潜在空间中的连续时间轨迹。与传统的基于离散时间戳的模型不同， SDE 天然适合于模拟连续的时间轨迹。SDE-EDG 建模了时序轨迹，可以通过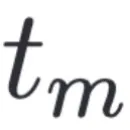
时刻的样本预测任意未来时刻
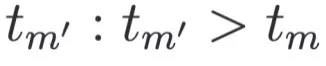的样本：
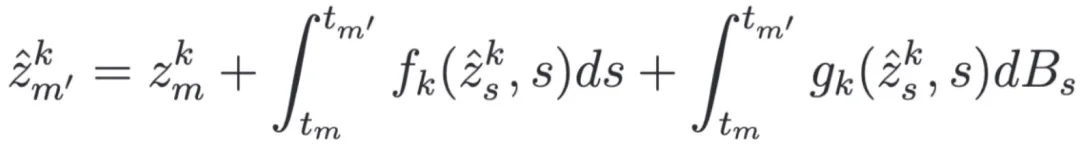
这里特征空间变量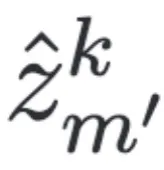
是由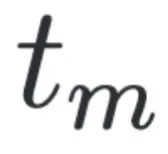
时刻的样本预测得到，
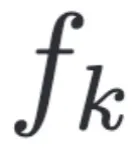是 drift function，
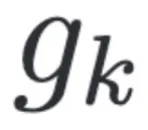是 diffusion function。
3. 路径对齐与最大似然估计：
SDE-EDG 通过最大化 IFGET 的似然估计来训练模型，
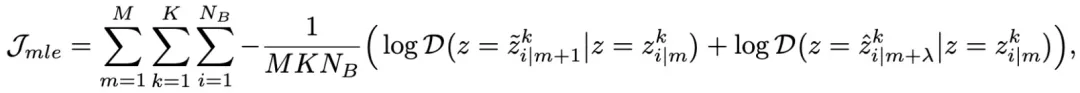
最终训练函数是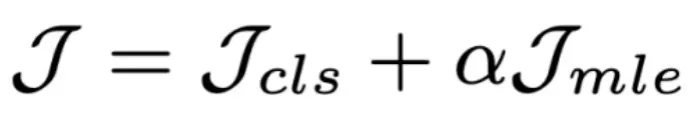
，第一项是预测分类任务误差损失函数。
4. 实验
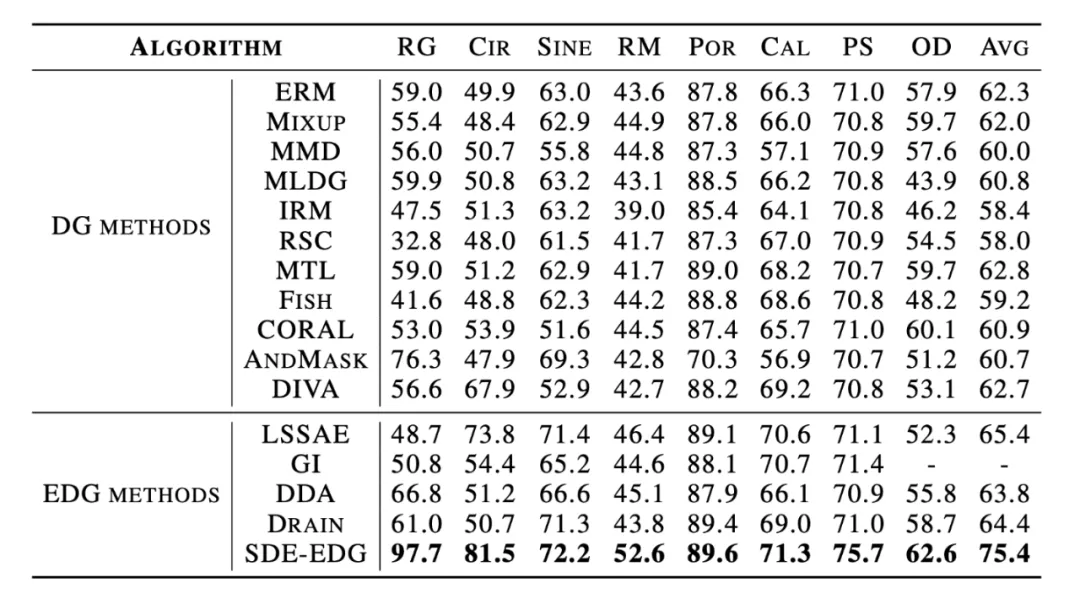
- 下表展示了 SDE-EDG 与其他基线方法在多个数据集上分类准确率的比较。这些数据集包括 Rotated Gaussian (RG), Circle (Cir), Rotated MNIST (RM), Portraits (Por), Caltran (Cal), PowerSupply (PS), 和 Ocular Disease (OD)。结果显示，SDE-EDG 在所有数据集上的平均准确率均优于其他方法。
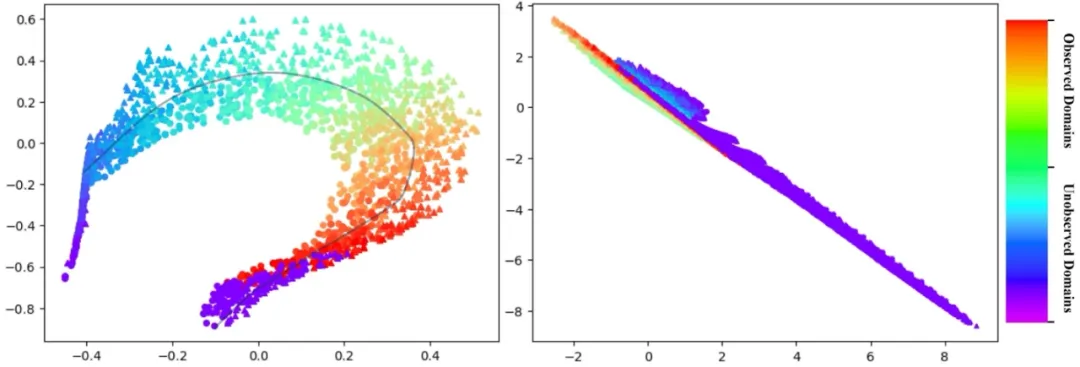
- 下图提供了一个直观的比较，展示了 SDE-EDG 算法（左）与传统 DG 方法 IRM（右）在特征表示方面的差异。通过数据特征空间的可视化，我们可以观察到 SDE-EDG 学习到的特征表示具有明显的决策边界，其中不同类别的数据点被清晰地区分开来，以不同形状表示，并且不同域的数据以彩虹条的颜色区分。这表明 SDE-EDG 能够成功捕捉数据随时间演变的动态，并在特征空间中保持类别的可分性。相比之下，IRM 的特征表示则倾向于将数据点坍缩到单一方向，导致决策边界不明显，这反映出 IRM 在捕捉时变分布趋势方面的不足。
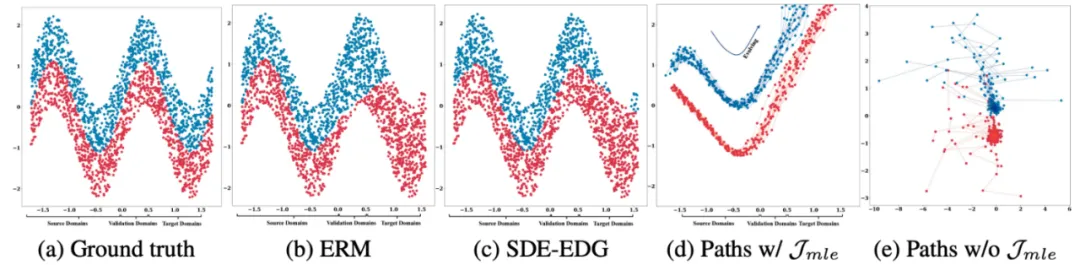
- 下图通过一系列子图深入展示了 SDE-EDG 算法在捕捉数据随时间演变的能力方面的优势。子图 (a) 提供了 Sine 数据集的真实标签分布，其中正例和负例用不同颜色的点表示，为后续的比较提供了基准。接着，子图 (b) 和 (c) 分别展示了基于 ERM 的传统方法和 SDE-EDG 算法对同一数据集的预测结果，通过对比可以看出 SDE-EDG 在捕捉数据演变模式上的明显优势。子图 (d) 和 (e) 进一步揭示了 SDE-EDG 学习到的演变路径，其中 (d) 展示了应用了路径对齐损失（最大似然损失函数）后的路径，而 (e) 展示了未应用该损失时的路径。通过这一对比，可以直观地看到路径对齐损失对于确保模型能够正确捕捉和表征数据随时间变化的重要性。
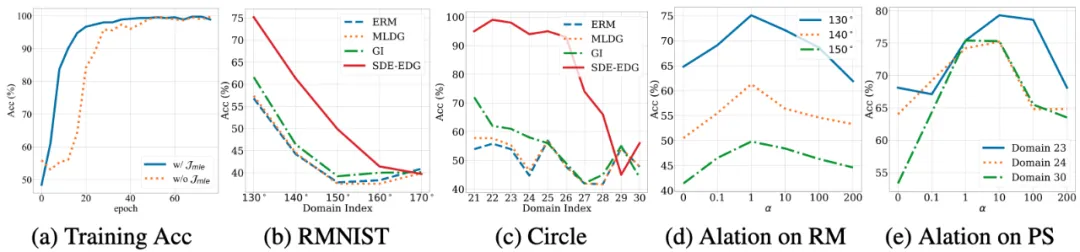
- 下图子图 (a) 展示了在 Portraits 数据集上，使用不同算法进行训练时的准确率收敛轨迹。这个子图提供了一个直观的视角，用以比较 SDE-EDG 算法与其他基线方法（如 ERM、MLDG、GI）在训练过程中性能的变化情况。通过观察训练准确率随时间推移的增长趋势，我们可以评估不同算法的学习能力和收敛速度。SDE-EDG 算法的收敛轨迹尤其值得关注，因为它揭示了该算法在适应不断演变的数据分布时的效率和稳定性。
下图子图 (b) 和 (c) 分别展示了 RMNIST 和 Circle 数据集上，SDE-EDG 算法在这些数据集上的表现显示出其在处理时变分布时的优越性，即使在面对较大时间跨度的目标域时，也能保持较高的准确率，这表明了 SDE-EDG 算法在捕捉和适应数据演变模式方面的强大能力。
下图子图 (d) 和 (e) 探讨了最大似然损失（Maximum Likelihood Loss）在 RMNIST 和 PowerSupply 数据集上对 SDE-EDG 性能的影响。通过改变正则化权重 α 的值，这两个子图展示了不同 α 设置对模型性能的具体影响。实验结果表明，适当的 α 值可以显著提高 SDE-EDG 在特定数据集上的性能，这强调了在实际应用中根据数据集特性和任务需求调整超参数的重要性。
结论
论文作者提出了一种新的 SDE-EDG 方法，用于建模时变域泛化（EDG）问题。方法涉及通过识别样本到样本的对应关系并生成连续插值样本来构建 IFGET。随后，作者采用随机微分方程（SDE）并将其与 IFGET 对齐进行训练。文章的贡献在于揭示了通过收集个体的时间轨迹来捕获演变模式的重要性，以及在时间间隔之间进行插值以减轻源时间戳数量有限的问题，这有效地防止了 SDE-EDG 对有限时间戳的过拟合。
