大语言模型产生幻觉、胡说八道的问题被诟病,已经不是一天两天了。
前有ChatGPT编造法律案件,后有谷歌搜索建议披萨放胶水。
就连号称模型更安全、幻觉更少的Claude系列,在Reddit上也能看到不少吐槽。
LLM输出虚假信息的问题,似乎并不能在短时间内彻底解决。
这就给很多场景下的应用带来了巨大的障碍,尤其是法律、医疗、学术这样比较严谨的知识领域。如果答案有错,还不如不用。
那么能不能有一种方法,至少为LLM的输出划定一个置信区间呢?
6月5日,DeepMind发表了一篇名为「To Believe or Not to Believe Your LLM」,就开始着手解决这个问题。
如果无法强迫LLM坚持输出真实信息,知道它什么时候在胡说八道也很重要。

论文地址:https://arxiv.org/abs/2406.02543
这篇论文由DeepMind Foundations团队出品,带头人是加拿大阿尔伯塔大学教授Csaba Szepesvari,他也是这篇论文的作者之一。

论文探讨了大语言模型中的不确定性量化问题,也就是说,旨在确定LLM的响应何时会出现较高的不确定性。
不确定性分为两个范畴,一个是认知不确定性(epistemic uncertainty),另一个是偶然不确定性(aleatoric uncertainty)。
前者是指对基本事实的不了解,比如,不清楚事实或者语言不通所造成的不确定性,可能来源于训练数据量或者模型容量不足。
后者则是一种不可约的随机性,比如同一个问题存在多种可能的答案。
LLM的工作本质是对文本的概率分布进行建模,因此会很自然地通过统计不确定性的视角看待问题的真实性。
以前的许多工作通过启发式的方法计算LLM回答的对数似然性,但这一般只适用于偶然不确定性较低的情况,也就是有「标准答案」的问题。
对于有多个正确答案的问题,需要将认知不确定性和偶然不确定性解耦。
因此,团队推导出了一种信息论度量(information-theoretic metric)方法,能可靠地检测出认知不确定性占多数的情况,这时我们就可以说,模型的输出没有那么可靠,Not to Believe!
这种方法根据什么来计算?
其实,可以完全基于模型的输出来考察,只需根据之前的回答进行一些特殊的迭代prompting即可。
有了这个量化方法,无论是面对有单一答案的问题,还是有多个可能答案的问题,都可以检测出回答中的幻觉,也就是认知不确定性很高的情况。
这和此前的不确定性量化策略相比,形成了鲜明对比,因为之前的方法都不能检测出多答案情况下的幻觉。
DeepMind Foundations团队进行了一系列实验,证明了他们方法的优势。
此外,研究还揭示了如何通过迭代prompting放大LLM指定给定输出的概率,这可能会引起人们的兴趣。
方法概述
首先,我们需要形成这样一个共识:
如果从基本事实(语言)中获得对同一查询的多个回复,那么它们应该是相互独立的。
也就是说,在概率论解释中,对于一个固定的查询,这些多个回复的联合分布必须是一个乘积分布。
基于这一点,我们就可以将其用于衡量LLM的输出与基本事实之间的距离。
由语言模型实现的序列模型允许我们构建多个响应的联合分布,基于LLM先前的响应和概率链规则,对LLM进行迭代prompting。
具体来说,先给定查询要求模型提供一个响应,然后将查询和相应输入给LLM,要求提供另一个响应,然后给定查询和前两个响应提供第三个响应,依此类推。
关键思路是,在对LLM进行迭代prompting的过程中,激发模型重复潜在回答,可以观察到不同的行为模式,反映不同程度的认知不确定性。。
如果模型对某个查询的认知不确定性较低,那么在prompting中重复一个不正确的回答不会显著增加其概率。
但是,如果认知不确定性较高,重复一个不正确的回答就会大大增加其概率。
下面是这一过程的prompt模板:

不断诱导LLM
下面的例子可以更好地解释这一过程——
给定问题:「英国的首都是什么?」通过在提示中重复错误答案(如巴黎),正确答案伦敦仍然保持很高的概率。
这意味着该模型的答案是确定的,它的认知不确定性较低。
相反,如果答案的概率发生了变化,那么模型就具有高度的认识不确定性。
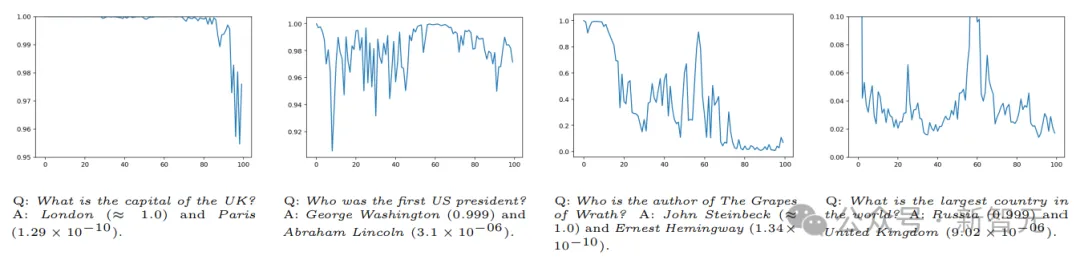
如上图最左边的示例所示,当我们将错误回答的重复次数增加到100次的时候,正确回答「伦敦 」的条件归一化概率从100%下降到大约 96%。
在这些示例中,最初对查询的回答的认识不确定性较低,即使在错误信息重复出现的情况下,正确回答的概率仍然很大。
可是当面对更有挑战性的问题时,模型就不那么容易「坚持己见 」了。
比如,问LLM「爱尔兰的民族乐器是什么?」,它回答「竖琴」和 「尤利安管 」的概率都很大(第一个答案是正确答案)。
这一次,通过多次在提示中加入错误的回答,正确答案的概率迅速下降到接近于零。
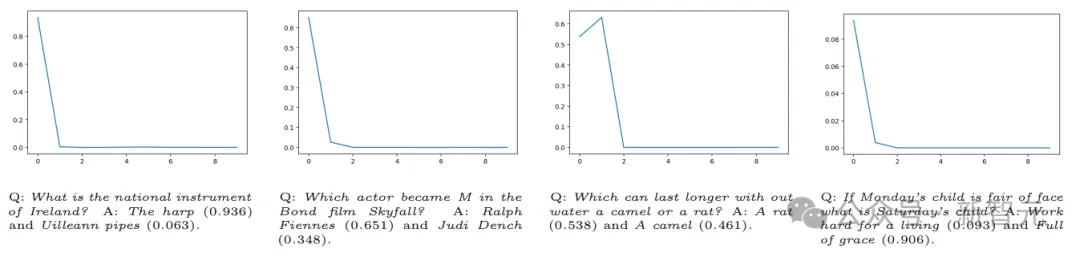
认知不确定性度量
在对LLM进行完上述观察,研究者推导出了一种信息论度量方法。
通过测量模型的输出分布对重复添加以前的(可能不正确的)提示回答的敏感程度,来量化认知不确定性。
更确切地说,如果LLM对之前的回复不敏感,模型就有了所需的独立性,并且LLM得出的联合分布可以任意接近基本事实。
如果正相反,上下文中的响应严重影响了模型的新响应,那么直观地说,LLM对其参数中存储的知识的置信度很低,因此LLM派生的联合分布不可能接近基本事实。
这一观察结果可用于区分高不确定性的两种情况:一种是偶然不确定性高,另一种是认知不确定性高。
最后,利用这一指标,论文介绍了一种基于互信息分数的幻觉检测算法M.I.。
通过应用链式规则,他们定义了多个响应的「伪联合分布 」,同时将之前的响应纳入提示。
这种伪联合分布的互信息可作为认知不确定性的下限。互信息的估计值可用作得分,表示LLM对给定查询产生幻觉的信念强度。
结果
论文在开放域问答基准上让Gemini 1.0 Pro进行闭卷回答,对这种基于互信息(MI)的方法进行了评估,包括TriviaQA、AmbigQA以及基于WordNet创建的一个多标签数据集。
实验中共使用了3种基线方法作为对比:T0表示贪婪方法选择的LLM回答,S.E.表示使用2023年提出的「语义熵」方法(semantic-entropy)选择的前10个回答,S.V.表示2022年提出的「自我验证」方法(self-verification)的一个版本。
对LLM的回答主要使用两个方面衡量,一是准确率,二是召回率。
准确率表示查询中正确决策的百分比,召回率则表示没有弃权的查询的百分比。
结果表明,与基线方法相比,该方法能有效检测幻觉(认识不确定性较高的输出),尤其是在处理包含单标签和多标签查询的数据集时。
在TriviaQA和AmbigQA数据集上,论文提出的M.I.方法与S.E.方法基本表现相当,但明显优于T0和S.V.。
而后两个数据集包含大量的高熵、多标签查询,此时M.I.方法明显优于S.E.方法。
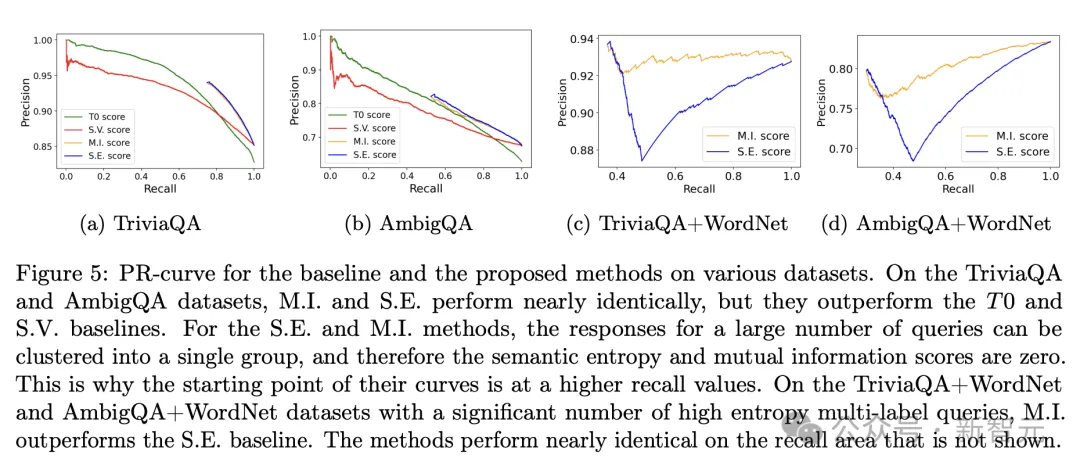
将LLM输出回答的熵进行分区后,分别查看两种方法的召回率和错误率,可以更直观地看到M.I.方法在高熵查询中的优越性能,不仅很少犯错误,而且召回值更高。
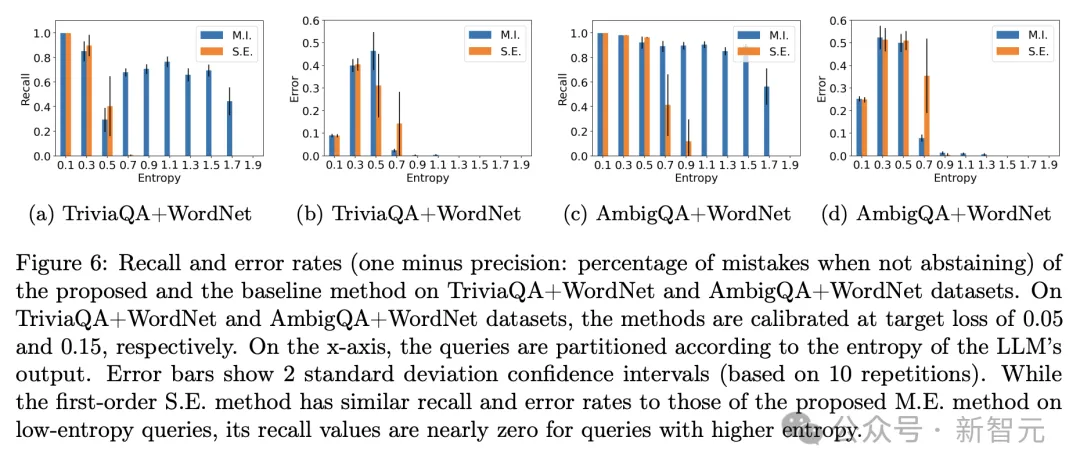
这篇论文相对于考虑LLM整体不确定性的一阶方法,将认知不确定性和任意不确定性分开考量,从而确定了LLM认知不确定性的可证明的下界。
此外,在认知不确定性视角下提出的基于互信息的弃权方法,能让LLM在混合单标签/多标签查询任务上取得更好的表现。





































