年前，Mamba被顶会ICLR拒稿的消息曾引起轩然大波。
甚至有研究人员表示：如果这种工作都被拒了，那我们这些「小丑」要怎么办？
这次，新一代的Mamba-2卷土重来、再战顶会，顺利拿下了ICML 2024！
仍是前作的两位大佬（换了个顺序），仍是熟悉的配方：
论文地址：https://arxiv.org/pdf/2405.21060
开源代码和模型权重：https://github.com/state-spaces/mamba
不同的是，作者在更高的视角上，统一了状态空间模型（SSM）和注意力机制（Attention），也就是文章标题所说的「Transformers are SSMs」。
——这下咱们都是一家人了，不用动不动就「打生打死」了。
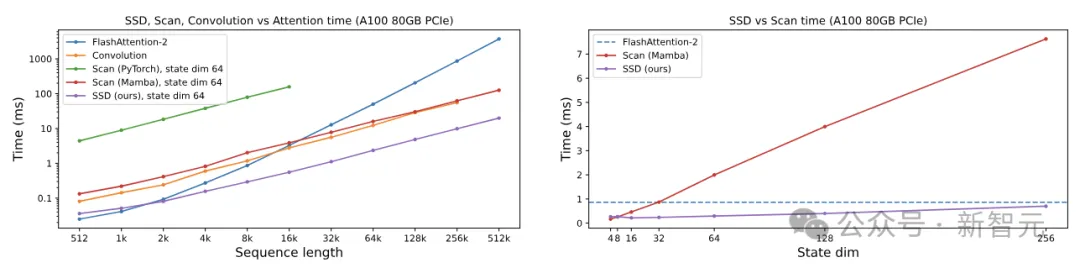
性能方面，Mamba-2采用了新的算法（SSD），比前代提速2-8倍，对比FlashAttention-2也不遑多让，在序列长度为2K时持平，之后便一路遥遥领先。
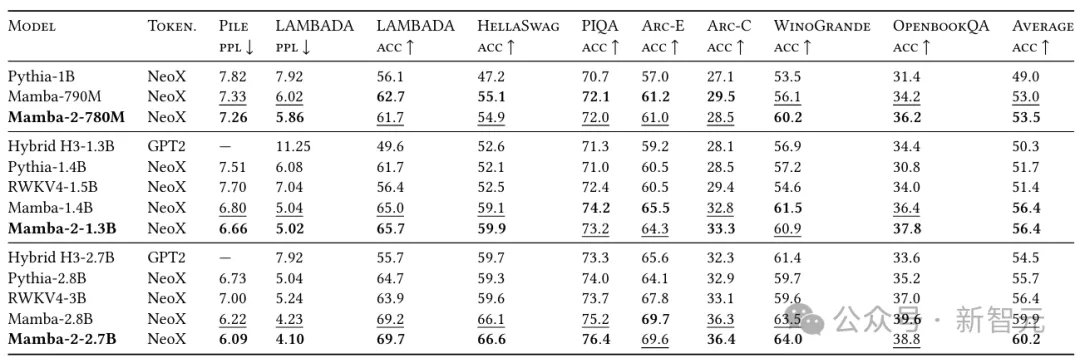
在Pile上使用300B token训练出的Mamba-2-2.7B，性能优于在同一数据集上训练的Mamba-2.8B、Pythia-2.8B，甚至是更大的Pythia-6.9B。
从理论上整合了SSM和Transformer，同等性能下，模型更小，消耗更低，速度更快。
更重要的是，能够利用GPU的硬件资源（矩阵乘法单元），以及针对Transformer的一系列优化。
——Mamba-2大有一统江湖之势。
1代Mamba，爆发式占领AI社区
事实上，关于1代Mamba的各种研究一直在爆发性地增长，arxiv已经被各种Mamba所占领，谷歌学术的引用量也达到了350多。
后续工作如雨后春笋一般冒出，包括视觉、基因组学、图表等的直接应用，以及回忆能力、上下文学习能力、形式语言表达能力等方面的研究。
作者兴奋地表示：「我们多年来一直在追求的高效序列模型研究路线，真正引起了机器学习社区的共鸣。」
唯一遗憾的是，Mamba遭到ICLR拒稿，所以关于Mamba到底有没有前途这个事也就被打上了问号。
现在，问题解决了，不但论文被接收了，而且还证明了Transformer和Mamba其实是一家人——
「你说我不行？那Transformer到底行不行？」
值得注意的是，之前很火的Vision Mamba以及另一篇关于Mamba的研究也杀入了ICML 2024。
对于改进Mamba的初衷，作者表示，当前AI社区的大家都在努力解决Transformer的问题，尽管SSM的特性和效果都相当好，但却跟社区的努力方向不一致。
这次的Mamba-2可以把针对Transformer的优化都用上，不浪费大家的努力。
新架构一统江湖
在介绍新架构之前，小编先帮大家简单理一下背景。
状态空间模型SSM之所以如此令人着迷，是因为它们显得如此之「基础」。
比如，它们与序列模型的许多主要范式，都有着丰富的联系。
它们似乎抓住了连续、卷积和循环序列模型的本质，把所有这些元素都包含在了一个简单优雅的模型里。
不过，另一个主要的序列模型范式——注意力机制的变体，却更加无所不在。
然而SSM却总感觉和Attention是脱节的。
在这里，研究者们发出了「灵魂拷问」——SSM和注意力之间的概念联系是什么？有无可能将二者结合起来？
那就要从公式说起了。
状态空间模型SSM可以这么定义：
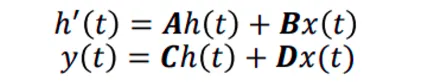
这是个微分方程，利用导数定义进行代换：
可以得到SSM的解：
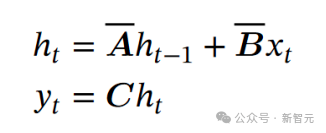
这个东西就跟RNN一毛一样了：
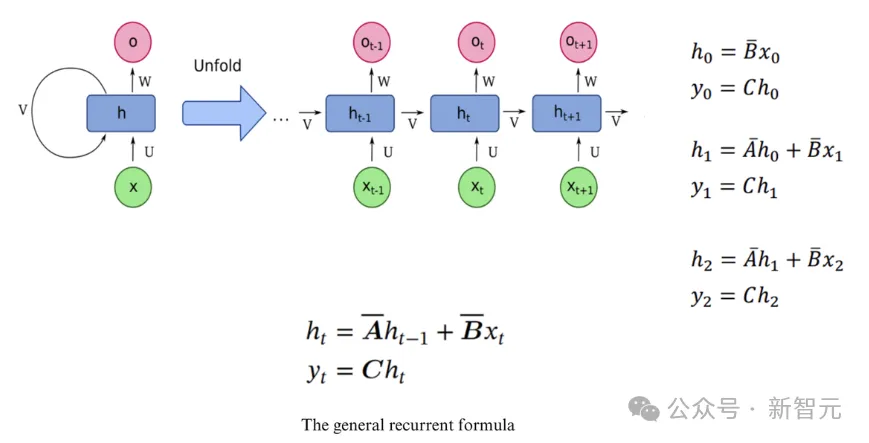
所以可以认为SSM等价于RNN。
如果将RNN的递归结构展开，那么它又可以等价于卷积：
此时，便可以利用卷积的特性进行并行训练，而进行推理时又可以享受RNN带来的O(1)复杂度。
当然，好事不能让你全占了，这种结构仍然逃不过固有的梯度爆炸（或消失），以及难以胜任选择性复制和上下文学习等任务。
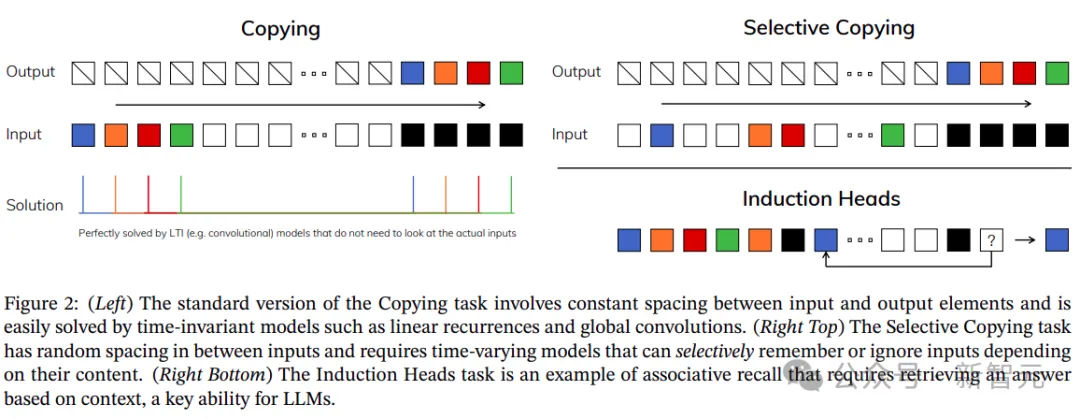
为此，Mamba在SSM的基础上加入了能够随输入变化的参数。
不过这样做的代价是失去了固定kernel带来的并行性，所以作者另辟蹊径，使用前缀和的方式来加速RNN的训练。
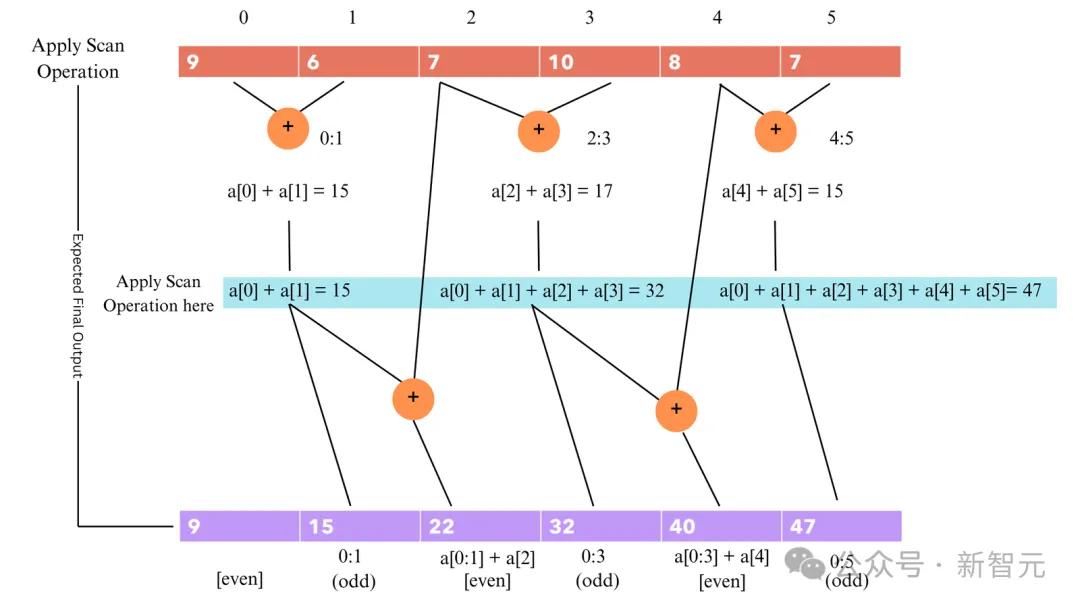
不过，从计算角度来看，Mamba在硬件效率上仍然远不如注意力机制。
原因在于，目前常用的GPU、TPU等加速器，是为矩阵乘法进行过专门优化的。
1代Mamba吃不到硬件矩阵运算单元的红利，尽管推理时有速度优势，但训练时问题就大了。
所以作者就想，我能不能把Mamba的计算重构成矩阵乘法呢？
于是，新一代的Mamba诞生了。
结构化状态空间对偶性：SSD
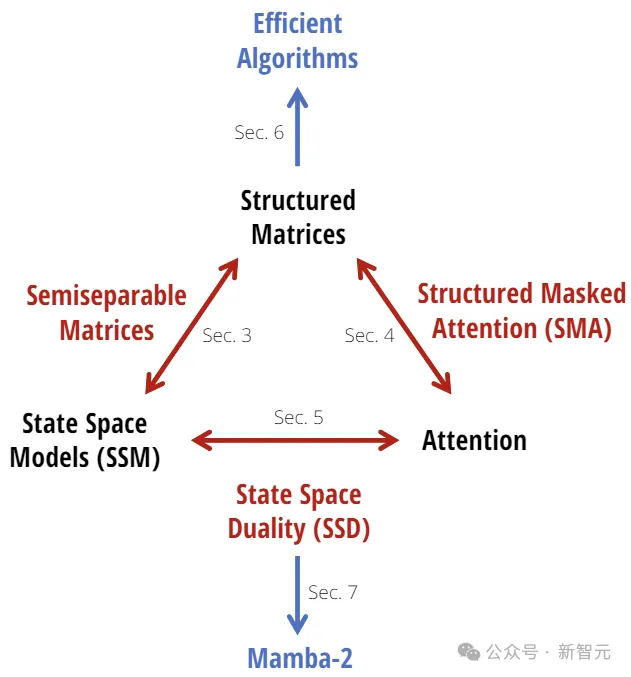
Mamba-2的核心，是结构化状态空间对偶性（State Space Duality，SSD）的概念：
1. SSD模型指的是一个特定的独立层，比如注意力层或状态空间模型（SSM），可以被整合到深度神经网络中；
2. SSD框架是一个用于推理该模型（以及更多理论连接）的通用框架；
3. SSD算法是一种比以前的SSM更高效地计算SSD层的算法。
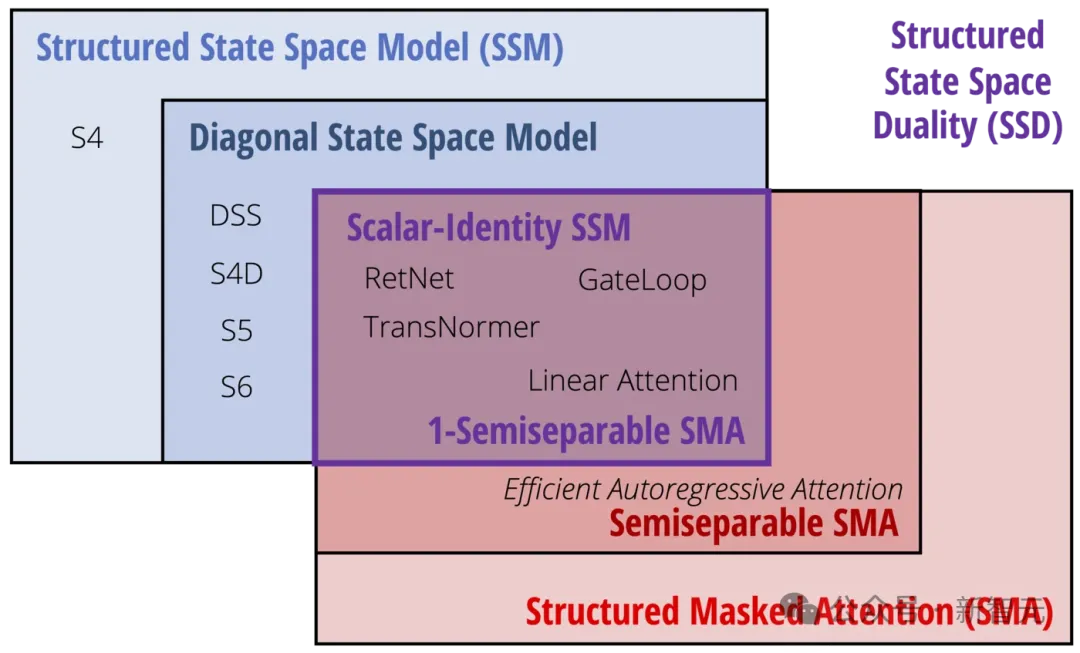
SSD框架（红色，蓝色）：状态空间模型（即半分离矩阵）和结构化掩码注意力涵盖了大量高效的序列模型。它们的交集就是SSD模型（紫色）
原始的Mamba（或更准确地说，其核心「S6」层）实际上是一个具有对角结构的选择性状态空间模型（SSM）。
Mamba-2的SSD层只做了一个小改动：它进一步限制了对角矩阵𝐴，使其成为标量乘以单位矩阵的结构。换句话说，𝐴的对角元素必须都是相同的值。
在这种情况下，𝐴可以表示为形状（𝑇），并且还可以将𝐴𝑡识别为一个标量（有时会表示为𝑎𝑡）。
所谓「对偶性」是指，方程（1）（标量-恒等结构𝐴𝑡的情况）和（3）中定义的两个模型实际上是完全相同的模型。
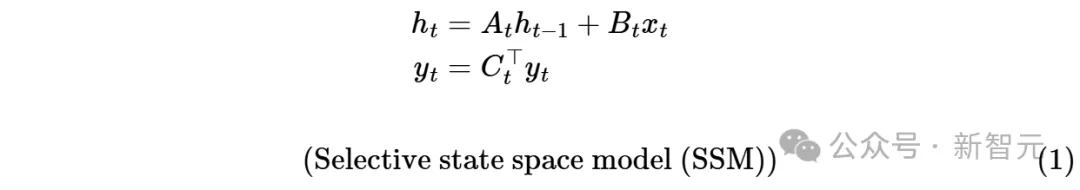
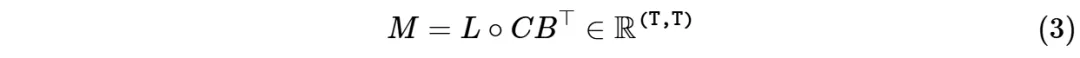
因此，我们可以将其视为一个特定函数：
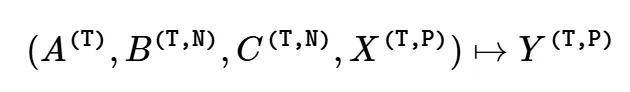
SSD vs. SSM
与之前的状态空间模型（SSM）相比，SSD在递归矩阵𝐴上增加了更多结构：
1. Mamba-1（S6）在矩阵𝐴上使用对角结构，而Mamba-2（SSD）在矩阵𝐴上使用标量乘以单位矩阵的结构；
2. Mamba-1的头维度是𝑃=1（即所有通道完全由独立的SSM控制），而Mamba-2使用的头维度是𝑃>1（默认情况下类似于𝑃=64）。
特别是，这可以通过两种方式视为权重共享：
1. 通过将矩阵𝐴的对角结构限制为标量乘以单位矩阵，递归动态在状态空间的所有𝑁元素之间共享；
2. 这些动态也在给定头的所有𝑃通道之间共享。
换句话说，一个单一的SSM头的总状态大小为𝑃×𝑁，在Mamba-1中由独立的标量递归控制，而在Mamba-2中由单一的共享递归控制。
而这些变化，主要就是为了提高效率——让模型能够以「双重注意形式」查看，从而允许使用矩阵乘法。
因此，与Mamba-1相比，Mamba-2支持更大的状态维度（从N=16提升到了N=64、N=256甚至更高），同时在训练期间速度更快。
SSD vs. Attention
与标准（自）注意力机制相比，SSD只有两点不同：
1. 取消了softmax归一化；
2. 以乘法方式应用单独的元素级掩码矩阵。
第一个不同之处在于，它将模型的有效状态大小从线性减少到常数，并将效率从二次方提升到了线性。
第二个不同之处是SSD与标准线性注意力的区别。一种理解掩码的方法是将其视为依赖于输入的相对位置编码，由于掩码𝐿的存在，标准的注意力得分𝑄𝑖𝐾𝑗会被一个权重𝑎𝑖:𝑗×=𝑎𝑖⋯𝑎𝑗+1所衰减，这可以理解为基于位置𝑖和𝑗之间距离的「折现细数」（discount factor）。
在注意力形式中，这种依赖输入的位置掩码可以解释为Mamba「选择性」的关键因素！
SSD算法
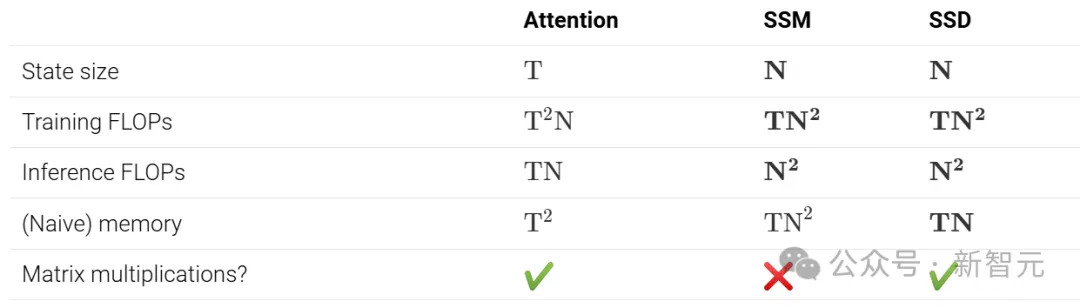
由于Mamba-1的算法和实现没有使用张量核心，因此只能进行小规模的状态扩展（通常为𝑁=16）。
相比之下，矩阵乘法的FLOPs要比非矩阵乘法快得多（最多快16倍）：
- A100 GPU有312 TFLOPS的BF16矩阵乘法性能，但只有19 TFLOPS的FP32算术性能；
- H100有989 TFLOPS的BF16矩阵乘法性能，但只有67 TFLOPS的FP32算术性能。
这次，Mamba-2的一个主要目标，便是利用张量核心来加速SSM。
由于SSD连接了SSM和结构化矩阵，计算SSM或线性注意力的高效算法，可以直接对应于「token混合」或「序列混合」矩阵𝑀的不同分解。
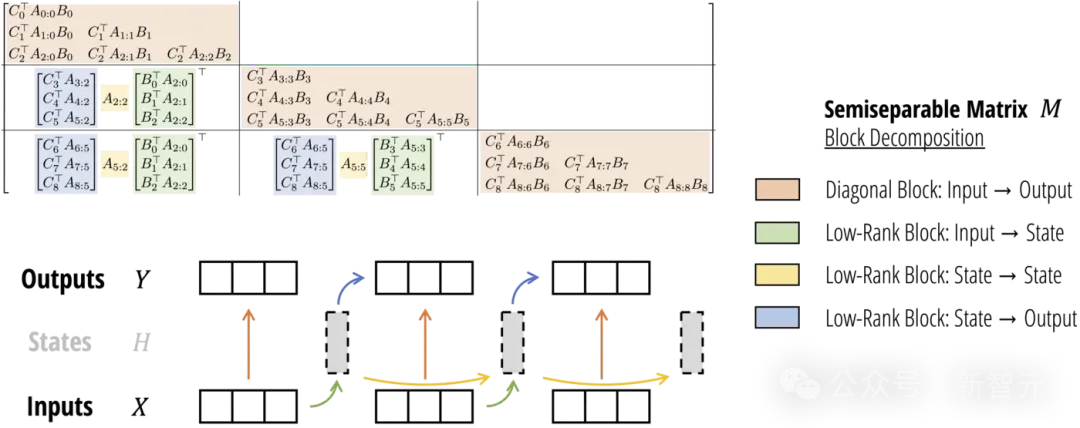
如今，这个算法不仅速度更快，而且比原始的Mamba选择性扫描更容易实现，仅需大约25行代码！
def segsum(x):"""Naive segment sum calculation. exp(segsum(A)) produces a 1-SS matrix,
which is equivalent to a scalar SSM."""
T = x.size(-1)
x_cumsum = torch.cumsum(x, dim=-1)
x_segsum = x_cumsum[..., :, None] - x_cumsum[..., None, :]
mask = torch.tril(torch.ones(T, T, device=x.device, dtype=bool), diagnotallow=0)
x_segsum = x_segsum.masked_fill(~mask, -torch.inf)return x_segsum
def ssd(X, A, B, C, block_len=64, initial_states=None):"""
Arguments:
X: (batch, length, n_heads, d_head)
A: (batch, length, n_heads)
B: (batch, length, n_heads, d_state)
C: (batch, length, n_heads, d_state)
Return:
Y: (batch, length, n_heads, d_head)
"""assert X.dtype == A.dtype == B.dtype == C.dtype
assert X.shape[1] % block_len == 0# Rearrange into blocks/chunks
X, A, B, C = [rearrange(x, "b (c l) ... -> b c l ...", l=block_len) for x in (X, A, B, C)]
A = rearrange(A, "b c l h -> b h c l")
A_cumsum = torch.cumsum(A, dim=-1)# 1. Compute the output for each intra-chunk (diagonal blocks)
L = torch.exp(segsum(A))
Y_diag = torch.einsum("bclhn,bcshn,bhcls,bcshp->bclhp", C, B, L, X)# 2. Compute the state for each intra-chunk# (right term of low-rank factorization of off-diagonal blocks; B terms)
decay_states = torch.exp((A_cumsum[:, :, :, -1:] - A_cumsum))
states = torch.einsum("bclhn,bhcl,bclhp->bchpn", B, decay_states, X)# 3. Compute the inter-chunk SSM recurrence; produces correct SSM states at chunk boundaries# (middle term of factorization of off-diag blocks; A terms)if initial_states is None:
initial_states = torch.zeros_like(states[:, :1])
states = torch.cat([initial_states, states], dim=1)
decay_chunk = torch.exp(segsum(F.pad(A_cumsum[:, :, :, -1], (1, 0))))
new_states = torch.einsum("bhzc,bchpn->bzhpn", decay_chunk, states)
states, final_state = new_states[:, :-1], new_states[:, -1]# 4. Compute state -> output conversion per chunk# (left term of low-rank factorization of off-diagonal blocks; C terms)
state_decay_out = torch.exp(A_cumsum)
Y_off = torch.einsum('bclhn,bchpn,bhcl->bclhp', C, states, state_decay_out)# Add output of intra-chunk and inter-chunk terms (diagonal and off-diagonal blocks)
Y = rearrange(Y_diag+Y_off, "b c l h p -> b (c l) h p")return Y, final_stateMamba-2架构
Mamba-2架构的核心贡献是提出了新的SSD层，及其理论，与此同时，研究者也对Mamba的神经网络架构做了一些小改变。
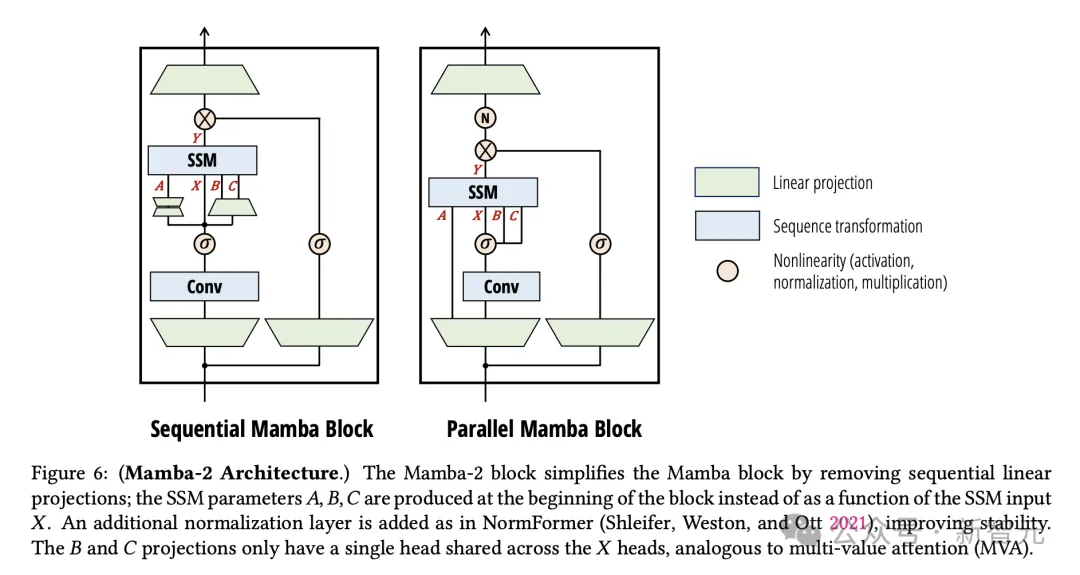
Mamba-2块通过删除连续线性映射来简化Mamba块：SSM参数𝐴, 𝐵, 𝐶是在块的开头生成的，而不是作为SSM输入𝑋的函数。如NormFormer中一样，添加了一个额外的归一化层，以提高稳定性。B和C映射只有一个在𝑋头之间共享的头，类似于多值注意力（MVA）
主要的变化是，𝑋输入并行生成（𝐴, 𝐵, 𝐶）SSM参数，而非按顺序生成。
之所以这样的做，与注意力有一定关系。但实际上，它更加简洁，易于使用张量并行等扩展技术。
此外，模型架构还有一些其他不同之处。不过，研究作者想要强调的是，这些架构更改并不是模型的真正要点。
论文中，研究人员主要讨论了两种设计选择，最终形成Mamba-2架构。
首先是，块设计。
1. 并行参数映射
在Mamba-2中，SSD层被视为从𝐴, 𝑋, 𝐵, → 𝑌 的映射。与标准注意力架构的类比，其中𝑋, 𝐵, 𝐶对应于并行创建的Q, K, V投影。
2. 额外归一化
在初步实验中，研究者发现在较大的模型中容易出现不稳定性。
他们通过在最终输出映射前的数据块中添加一个额外的归一化层（如LayerNorm、GroupNorm或RMSNorm）来缓解这一问题。
这种归一化的用法与NormFormer架构有最直接的关系，后者也在MLP和MHA块的末尾添加了归一化层。
此外，研究者还发现，这种变化与最近从线性注意力角度衍生而来，并与Mamba-2相关的模型类似。
最初的线性注意力公式通过一个分母项，进行了归一化，它模仿了标准注意力中softmax函数的归一化。
在TransNormerLLM和RetNet研究中，却发现了这种归一化不稳定性。因此在线性注意力层之后增加了一个额外的LayerNorm或GroupNorm。
研究者提出的「额外归一化层」与此前研究策略有不同，这是在「乘法门」分支之后加入的归一化层。
其次是，序列转换多头模式。
此前，曾提到了SSM被定义为序列转换，其中：
- 𝐴, 𝐵, 𝐶参数的状态维度是N；
- 它们定义了序列转换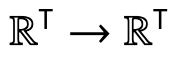
，比如可以表示为矩阵
；
- 这一转换只针对输入序列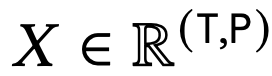
进行操作，并独立于P轴。
总而言之，大家可以将其视为，定义序列转换的一个头。
多头序列变换由H个独立的头组成，模型总维度为D=d_model。这些参数在多头之间是共享的，从而形成一个头模式（head pattern）。
状态大小N和头维度P，分别类似于注意力的𝑄头维度和𝑉头维度。
正如现代Transformer架构，在Mamba-2中，研究牛人员通常将这些维度，选择为64或128左右的常数。
当模型维度D增加时，便会增加头数量，同时保持头维度N和P不变。
为了说明如何做到这一点，研究人员可以将多头注意力的思想进行移植和扩展，从而为SSM或任何一般序列变换定义类似的模式。
1. 多头SSM（MHS） / 多头注意力（MHA）模式
经典多头注意力（MHA）模式假定头维度P，能够被模型维度D整除。头的数量H被定义为H=D/P。
然后，通过为每个参数创建H个独立的副本，就构建出了H个独立序列变换的「头」副本。
值得注意的是，虽然MHA模式最初只是针对注意力序列变换而描述的，但其可以应用到任何符合定义的序列变换上。
比如，上图中，多头SSD层将接受形状如公式 (17) 所示的输入，其中SSD算法被复制到了H=n_heads维度上。
2. 多合约SSM（MCS） / 多查询注意（MQA）模式
多查询注意力，是对注意力的一种巧妙优化，可以显著提高自回归推理的速度，它依赖于缓存𝑉张量。
这一技术只需避免给𝐾和𝑉额外的头维度，或者换句话说，将（𝐾, 𝑉）的单个头广播到𝑄的所有查询头。
利用状态空间对偶性（SSD），便可以多头注意力（MQA）定义为与方程 (18) 等效的的状态空间模型（SSM）。
在这里，𝑋和𝐵（分别对应注意力机制中的V和K）在H个头之间共享。
由于控制SSM状态收缩的𝐶参数，在每个头中都有独立的副本，因此研究人员也将其称之为多合约SSM（MCS）头模式。
类似地，研究人员还可以定义一种多键注意力（MKA），或多扩展SSM（MES）头模式。其中𝐵（控制SSM扩展）在每个头中是独立的，而𝐶和𝑋则在所有的头中共享。
3. 多输入SSM（MIS）/多值注意力（MVA）模式
虽然MQA因其KV缓存而受到关注，但它并不是SSM的自然选择。
相反，在Mamba中，𝑋被视为SSM的主要输入，因此𝐵和𝐶是输入通道共享的参数。
研究人员在公式（20）中定义了新的多输入SSM（MIS）模式的多值注意（MVA），它同样可以应用于任何序列变换，如SSD。
有了以上词汇，现在便可以更准确地描述最初的Mamba架构。
Mamba架构的选择性SSM（S6）层具有的特征是：
- 头维度𝑃=1：每个通道都有独立的SSM动态𝐴；
- 多输入SSM（MIS）或多值注意力（MVA）头结构：矩阵𝐵、𝐶（对应于注意力对偶性中的K、Q应）在输入𝑋（对应于注意力中的V）的所有通道中共享。
当然，作者表示，也可以在应用SSD时，去掉这些头模式的辩题。
有趣的是，尽管在参数数量和总状态维度上都有所控制，但在下游性能上却存在明显差异。他们根据经验发现Mamba最初使用的MVA模式性能最佳。
第三是，分组头模式。
多查询注意力的理念可以扩展到分组查询注意力：与使用1个K和V头不同，它可以创建G个独立的K和V头，其中1<G，而且G可以整除H。
这样做有两个动机：一是弥合多查询注意力和多头注意力性能差距，二是通过将G设置为分片数（shards）的倍数，以实现更高效的张量并行。
最后，研究人员还提到了线性注意力的其他SSD扩展项。
比如，核注意力近似于Softmax注意力，指数核特征图。
语言建模
论文中，虽没有像Mamba-1那样广泛地测试Mamba-2，但作者认为新架构总体上可与第一代性能相当，或者更好。
另外，研究称，全语言模型结果使用与Mamba相同的协议，并且在Chinchilla Law上的扩展性略好于Mamba。
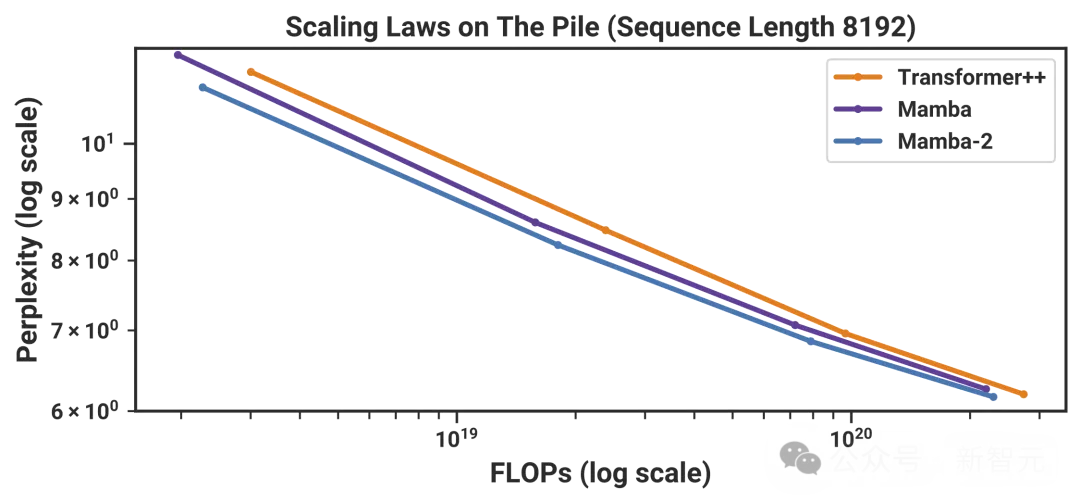
Pile数据集上的充分训练的模型，以及标准的零样本下游任务评估中，也看到了类似的趋势。
即使在性能相当的情况下，Mamba-2的训练速度也比初代Mamba快得多！
合成语言建模：MQAR
更有趣的是，研究者针对Mamba-2再次尝试了一项合成任务。
初代Mamba论文中，曾研究了「合成复制」和「诱导头」等合成任务后，后续研究中开始研究更难的联想回忆任务。
目前，由Zoology和Based团队引入的多查询联想回忆（MQAR），已经成为行业里的事实标准。
这次，研究人员测试了一个更难的版本，结果发现，Mamba-2的性能显著优于Mamba-1。
其中一个原因是，新架构的「状态」要大得多——最多是Mamba-1的16倍。这也是Mamba-2的设计初衷之一
另外，即便是在控制状态大小的情况下，Mamba-2在这一特定任务上的表现也明显优于Mamba-1。
系统和扩展优化
好在，Transformer诞生后，整个研究界和大公司已经对它进行了长达7年的系统优化。
SSD框架在SSM和注意力之间建立联系后，也可以让我们为Mamba-2等模型实现很多类似的优化。
为此，研究者的重点，就是用于大规模训练的张量并行和序列并行，以及用于高效微调和推理的变长序列。
张量并行
使用张量并行（TP）进行Mamba-1的大规模训练时，一个难点在于，它每层需要进行2次全归约（all-reduce），而Transformer中的注意力或MLP层，每层只需1次全归约。
这是因为，一些SSM参数是内部激活的函数，而不是层输入的函数。
在Mamba-2中，采用了「并行投影」结构，所有SSM参数都是层输入的函数，因此，就可以轻松地将TP应用于输入投影。
将输入投影和输出投影矩阵，根据TP的程度分成2、4、8个分片。
使用分组归一化，分组数量可被TP程度整除，这样每个GPU都能单独进行归一化。就是这些改变，使得每层只需1次全归约，而不是2次。
序列并行
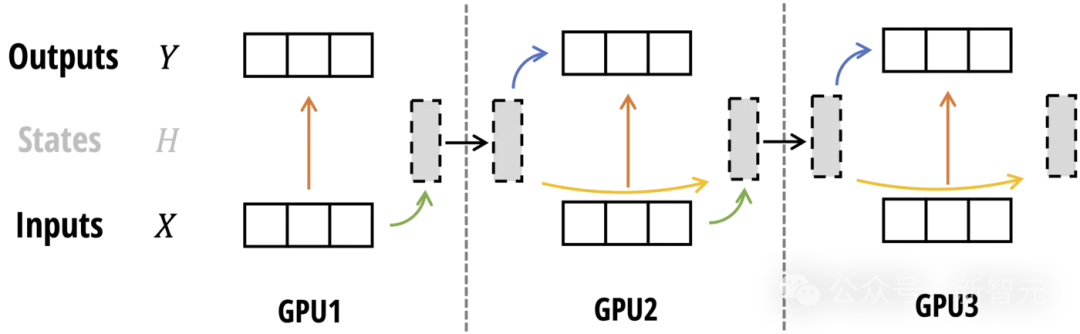
在训练非常长的序列时，可能需要沿序列长度进行拆分，并将不同部分分配给不同的设备。
有两种主要的序列并行（SP）形式：对于残差和归一化操作，这种形式将TP中的全归约替换为规约-散布、残差+归一化，然后是all-gather。
由于Mamba-2使用与Transformer相同的残差和归一化结构，这种SP形式可以直接应用，无需修改。
对于注意力或SSM操作，也称为上下文并行（CP）。
对于注意力机制，可以使用Ring注意力沿序列维度进行拆分。
对于Mamba-2，SSD框架又再次帮了大忙：使用相同的块分解，就可以让每个GPU计算其本地输出和最终状态，然后在更新每个GPU的最终输出之前，在GPU之间传递状态。
可变长度
在微调和推理过程中，同一批次中经常会出现不同长度的序列。
对于Transformer，通常会采用填充方式使所有序列长度相同（虽然会浪费计算资源），或者专门为可变长度序列实现注意力机制，并进行负载平衡。
而对于SSM，就可以将整个批次视为一个长「序列」，并通过将每个序列末尾token的状态转移𝐴𝑡设置为0，避免在批次中的不同序列之间传递状态。
结果
结果显示，更快的SSD算法，直接能让我们将状态维度增加到64或128！而在Mamba-1中，维度仅为16。
尽管从技术角度看，对于相同的𝑁，Mamba-2比Mamba-1受到的限制会更多，然而更大的状态维度，带来的结果通常就是模型质量的提升。
更受限制，但更大的状态维度通常会提升模型质量。
比如我们开头所见的，在Pile上训练3000亿tokens，Mamba-2的表现就明显优于Mamba-1和Pythia。
而混合模型的表现，也很令人满意。
从最近的Jamba和Zamba的工作中，研究者发现，将Mamba层与注意力层结合，可以超过纯Transformer或Mamba模型的性能。
在2.7B参数和3000亿tokens规模上验证一个仅包含6个注意力块（和58个SSD块）的混合模型后可以发现，其表现优于64个SSD块以及标准的Transformer++基线模型（32个门控MLP和32个注意力块）。
混合Mamba/注意力模型的下游评估
而且，对于相同的状态维度，SSD算法比Mamba-1的选择性扫描算法快得多，并且在计算上更能扩展到更大的状态维度。
其中的关键就在于，要充分利用张量核心的强大计算能力！
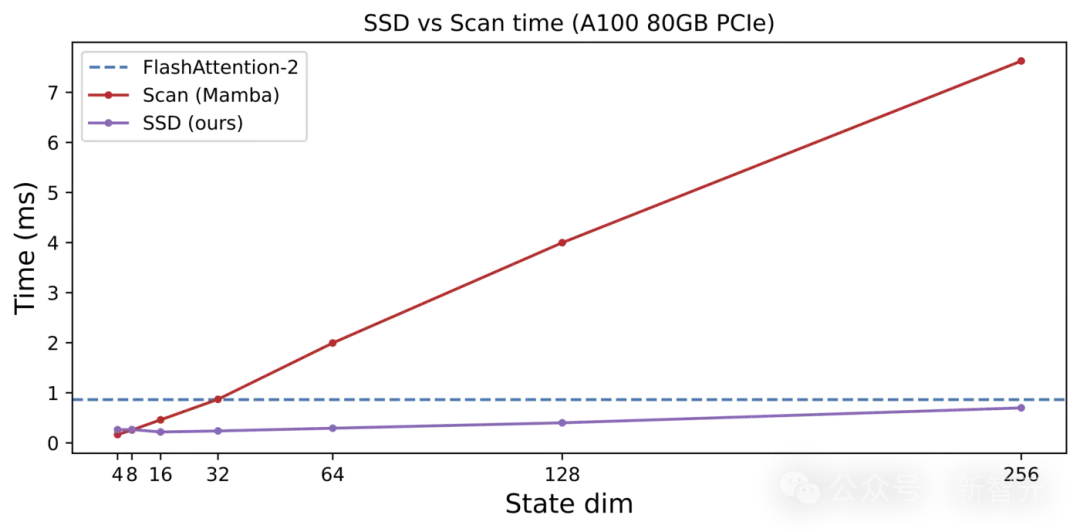
序列长度2K的效率基准
未来方向
如今，线性注意力和SSM连接起来后，前途一片大好，更快的算法、更好的系统优化，就在眼前了。
作者提出，接下来AI社区需要探索的，有以下三个方向——
理解：含有少量（4-6）注意力层的混合模型表现非常出色，甚至超过了纯Mamba（-2）或Transformer++。
这些注意力层的作用是什么？它们能被其他机制替代吗？
训练优化：尽管SSD可能比注意力机制更快，但由于Transformer中的MLP层非常适合硬件，整体上Mamba-2在短序列长度（例如2K）上，可能仍然比Transformer慢。
未来，是不是可以让SSD利用H100的新特性，让SSM在2-4K序列长度的大规模预训练中，比Transformer还快？
推理优化：有许多针对Transformers的优化方法，特别是处理KV缓存（量化、推测性解码）。
如果，模型状态（如SSM状态）不再随着上下文长度扩展，KV缓存不再是瓶颈，那时的推理环境，会如何变化？
