超强！必会的十大机器学习算法-51CTO.COM

1.线性回归

线性回归是用于预测建模的最简单且使用最广泛的机器学习算法之一。

它是一种监督学习算法，用于根据一个或多个自变量预测因变量的值。

定义

线性回归的核心是根据观察到的数据拟合线性模型。

线性模型由以下方程表示：

其中

是因变量（我们想要预测的变量）
是自变量（我们用来进行预测的变量）
是直线的斜率
是 y 轴截距（直线与 y 轴的交点）

线性回归算法涉及找到通过数据点的最佳拟合线。这通常是通过最小化观测值和预测值之间的平方差之和来完成的。

评估指标

均方误差 (MSE)：测量误差平方的平均值。值越低越好。
R平方：表示可以根据自变量预测的因变量变异的百分比。越接近 1 越好。

from sklearn.datasets import load_diabetes
from sklearn.model_selection import train_test_split
from sklearn.linear_model import LinearRegression
from sklearn.metrics import mean_squared_error, r2_score

# Load the Diabetes dataset
diabetes = load_diabetes()
X, y = diabetes.data, diabetes.target

# Splitting the dataset into training and testing sets
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2, random_state=42)

# Creating and training the Linear Regression model
model = LinearRegression()
model.fit(X_train, y_train)

# Predicting the test set results
y_pred = model.predict(X_test)

# Evaluating the model
mse = mean_squared_error(y_test, y_pred)
r2 = r2_score(y_test, y_pred)

print("MSE is:", mse)
print("R2 score is:", r2)

2.逻辑回归

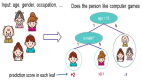
逻辑回归用于分类问题。它预测给定数据点属于某个类别的概率，例如是/否或 0/1。

评估指标

准确度：准确度是正确预测的观测值与总观测值的比率。
精确度和召回率：精确度是正确预测的正观察值与所有预期的正观察值的比率。召回率是正确预测的积极观察与实际中所有观察的比例。
F1 分数：召回率和精确率之间的平衡。

from sklearn.datasets import load_breast_cancer
from sklearn.linear_model import LogisticRegression
from sklearn.model_selection import train_test_split
from sklearn.metrics import accuracy_score, precision_score, recall_score, f1_score


# Load the Breast Cancer dataset
breast_cancer = load_breast_cancer()
X, y = breast_cancer.data, breast_cancer.target

# Splitting the dataset into training and testing sets
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2, random_state=42)

# Creating and training the Logistic Regression model
model = LogisticRegression(max_iter=10000)
model.fit(X_train, y_train)

# Predicting the test set results
y_pred = model.predict(X_test)

# Evaluating the model
accuracy = accuracy_score(y_test, y_pred)
precision = precision_score(y_test, y_pred)
recall = recall_score(y_test, y_pred)
f1 = f1_score(y_test, y_pred)

# Print the results
print("Accuracy:", accuracy)
print("Precision:", precision)
print("Recall:", recall)
print("F1 Score:", f1)

3.决策树

决策树是多功能且强大的机器学习算法，可用于分类和回归任务。

它们因其简单性、可解释性以及处理数值和分类数据的能力而广受欢迎。

定义

决策树由代表决策点的节点、代表可能结果的分支以及代表最终决策或预测的叶子组成。

决策树中的每个节点对应一个特征，分支代表该特征的可能值。

构建决策树的算法涉及根据不同特征的值递归地将数据集分割成子集。目标是创建同质子集，其中目标变量（我们想要预测的变量）在每个子集中都是相似的。

分裂过程持续进行，直到满足停止标准，例如达到最大深度、最小样本数，或者无法进行进一步改进。

评估指标

对于分类：准确率、精确率、召回率和 F1 分数
对于回归：均方误差 (MSE)、R 平方

from sklearn.datasets import load_wine
from sklearn.tree import DecisionTreeClassifier

# Load the Wine dataset
wine = load_wine()
X, y = wine.data, wine.target

# Splitting the dataset into training and testing sets
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2, random_state=42)

# Creating and training the Decision Tree model
model = DecisionTreeClassifier(random_state=42)
model.fit(X_train, y_train)

# Predicting the test set results
y_pred = model.predict(X_test)

# Evaluating the model
accuracy = accuracy_score(y_test, y_pred)
precision = precision_score(y_test, y_pred, average='macro')
recall = recall_score(y_test, y_pred, average='macro')
f1 = f1_score(y_test, y_pred, average='macro')

# Print the results
print("Accuracy:", accuracy)
print("Precision:", precision)
print("Recall:", recall)
print("F1 Score:", f1)

4.朴素贝叶斯

朴素贝叶斯分类器是一系列简单的 “概率分类器”，它们使用贝叶斯定理和特征之间的强（朴素）独立性假设。它特别用于文本分类。

它计算给定每个输入值的每个类别的概率和每个类别的条件概率。然后使用这些概率根据最高概率对新值进行分类。

评估指标：

准确性：衡量模型的整体正确性。
精确率、召回率和 F1 分数：在类别分布不平衡的情况下尤其重要。

from sklearn.datasets import load_digits
from sklearn.naive_bayes import GaussianNB

# Load the Digits dataset
digits = load_digits()
X, y = digits.data, digits.target

# Splitting the dataset into training and testing sets
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2, random_state=42)

# Creating and training the Naive Bayes model
model = GaussianNB()
model.fit(X_train, y_train)

# Predicting the test set results
y_pred = model.predict(X_test)

# Evaluating the model
accuracy = accuracy_score(y_test, y_pred)
precision = precision_score(y_test, y_pred, average='macro')
recall = recall_score(y_test, y_pred, average='macro')
f1 = f1_score(y_test, y_pred, average='macro')

# Print the results
print("Accuracy:", accuracy)
print("Precision:", precision)
print("Recall:", recall)
print("F1 Score:", f1)

5.K-最近邻（KNN）

K 最近邻 (KNN) 是一种简单直观的机器学习算法，用于分类和回归任务。

它根据输入数据点与其在特征空间中最近邻居的相似性进行预测。

在 KNN 中，新数据点的预测由其 k 个最近邻的多数类（用于分类）或平均值（用于回归）确定。KNN 中的 “k” 表示要考虑的邻居数量，这是用户选择的超参数。

算法

KNN 算法包括以下步骤

计算距离：计算新数据点与数据集中所有其他数据点之间的距离。
查找邻居：根据计算的距离选择 k 个最近邻居。
多数投票或平均：对于分类，分配 k 个邻居中出现最频繁的类标签。对于回归，计算 k 个邻居的目标变量的平均值。
进行预测：将预测的类标签或值分配给新数据点。

评估指标

「分类」：准确率、精确率、召回率、F1 分数。
「回归」：均方误差 (MSE)、R 平方。

from sklearn.datasets import load_wine
from sklearn.model_selection import train_test_split
from sklearn.neighbors import KNeighborsClassifier
from sklearn.metrics import accuracy_score, precision_score, recall_score, f1_score

# Load the Wine dataset
wine = load_wine()
X, y = wine.data, wine.target

# Splitting the dataset into training and testing sets
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2, random_state=42)

# Creating and training the KNN model
knn_model = KNeighborsClassifier(n_neighbors=3)
knn_model.fit(X_train, y_train)

# Predicting the test set results
y_pred_knn = knn_model.predict(X_test)

# Evaluating the model
accuracy_knn = accuracy_score(y_test, y_pred_knn)
precision_knn = precision_score(y_test, y_pred_knn, average='macro')
recall_knn = recall_score(y_test, y_pred_knn, average='macro')
f1_knn = f1_score(y_test, y_pred_knn, average='macro')

# Print the results
print("Accuracy:", accuracy_knn)
print("Precision:", precision_knn)
print("Recall:", recall_knn)
print("F1 Score:", f1_knn)

6.SVM

支持向量机 (SVM) 是一种强大的监督学习算法，用于分类和回归任务。

它们在高维空间中特别有效，广泛应用于图像分类、文本分类和生物信息学等各个领域。

算法原理

支持向量机的工作原理是找到最能将数据分为不同类别的超平面。

选择超平面以最大化边距，即超平面与每个类的最近数据点（支持向量）之间的距离。

SVM 还可以通过使用核函数将输入空间转换为可以线性分离的高维空间来处理非线性数据。

训练 SVM 的算法包括以下步骤：

数据准备：预处理数据并根据需要对分类变量进行编码。
选择核：选择合适的核函数，例如线性、多项式或径向基函数 (RBF)。
模型训练：通过寻找使类之间的间隔最大化的超平面来训练 SVM。
模型评估：使用交叉验证或保留验证集评估 SVM 的性能。

评估指标

「分类」：准确率、精确率、召回率、F1 分数。
「回归」：均方误差 (MSE)、R 平方。

from sklearn.svm import SVC

breast_cancer = load_breast_cancer()
X, y = breast_cancer.data, breast_cancer.target

# Splitting the dataset into training and testing sets
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2, random_state=42)

# Creating and training the SVM model
svm_model = SVC()
svm_model.fit(X_train, y_train)

# Predicting the test set results
y_pred_svm = svm_model.predict(X_test)

# Evaluating the model
accuracy_svm = accuracy_score(y_test, y_pred_svm)
precision_svm = precision_score(y_test, y_pred_svm, average='macro')
recall_svm = recall_score(y_test, y_pred_svm, average='macro')
f1_svm = f1_score(y_test, y_pred_svm, average='macro')

accuracy_svm, precision_svm, recall_svm, f1_svm

# Print the results
print("Accuracy:", accuracy_svm)
print("Precision:", precision_svm)
print("Recall:", recall_svm)
print("F1 Score:", f1_svm)

7.随机森林

随机森林是一种集成学习技术，它结合了多个决策树来提高预测性能并减少过度拟合。

它们广泛用于分类和回归任务，并以其鲁棒性和多功能性而闻名。

算法步骤

随机森林是根据数据集的随机子集并使用特征的随机子集进行训练的决策树的集合。

森林中的每棵决策树独立地进行预测，最终的预测是通过聚合所有树的预测来确定的。

构建随机森林的算法包括以下步骤

随机采样：从数据集中随机选择样本子集（带替换）来训练每棵树。
特征随机化：随机选择每个节点的特征子集以考虑分割。
树构建：使用采样数据和特征构建多个决策树。
投票或平均：聚合所有树的预测以做出最终预测。

评估指标

分类：准确率、精确率、召回率、F1 分数。
回归：均方误差 (MSE)、R 平方。

from sklearn.ensemble import RandomForestClassifier

breast_cancer = load_breast_cancer()
X, y = breast_cancer.data, breast_cancer.target

# Splitting the dataset into training and testing sets
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2, random_state=42)


# Creating and training the Random Forest model
rf_model = RandomForestClassifier(random_state=42)
rf_model.fit(X_train, y_train)

# Predicting the test set results
y_pred_rf = rf_model.predict(X_test)

# Evaluating the model
accuracy_rf = accuracy_score(y_test, y_pred_rf)
precision_rf = precision_score(y_test, y_pred_rf, average='macro')
recall_rf = recall_score(y_test, y_pred_rf, average='macro')
f1_rf = f1_score(y_test, y_pred_rf, average='macro')

# Print the results
print("Accuracy:", accuracy)
print("Precision:", precision)
print("Recall:", recall)
print("F1 Score:", f1)

8.K-均值聚类

K 均值聚类是一种无监督学习算法，用于将数据分组为 “K” 个聚类。确定 k 个质心后，每个数据点被分配到最近的簇。

该算法将数据点分配给一个簇，使得数据点与簇质心之间的平方距离之和最小。

评估指标

「惯性」：样本到最近聚类中心的总平方距离称为惯性。值越低越好。
「Silhouette Score」：表示一个项目属于其自身集群的紧密程度。高轮廓分数意味着该项目与其自身的集群匹配良好，而与附近的集群匹配不佳。轮廓得分从 -1 到 1。

from sklearn.datasets import load_iris
from sklearn.cluster import KMeans
from sklearn.metrics import silhouette_score

# Load the Iris dataset
iris = load_iris()
X = iris.data

# Applying K-Means Clustering
kmeans = KMeans(n_clusters=3, random_state=42)
kmeans.fit(X)

# Predicting the cluster for each data point
y_pred_clusters = kmeans.predict(X)

# Evaluating the model
inertia = kmeans.inertia_
silhouette = silhouette_score(X, y_pred_clusters)

print("Inertia:", inertia)
print("Silhouette:", silhouette)

9.PCA

降维是通过使用主成分分析 (PCA) 来完成的。它将数据转换为新的坐标系，减少变量数量，同时尽可能多地保留原始数据的变化。

使用 PCA 可以找到使数据方差最大化的主要成分或轴。第一个主成分捕获最大方差，第二个主成分（与第一个主成分正交）捕获第二大方差，依此类推。

评估指标

「解释方差」：表示每个主成分捕获的数据方差有多少。
「总解释方差」：由所选主成分解释的累积方差。

from sklearn.datasets import load_breast_cancer
from sklearn.decomposition import PCA
import numpy as np

# Load the Breast Cancer dataset
breast_cancer = load_breast_cancer()
X = breast_cancer.data

# Applying PCA
pca = PCA(n_compnotallow=2)  # Reducing to 2 dimensions for simplicity
pca.fit(X)

# Transforming the data
X_pca = pca.transform(X)

# Explained Variance
explained_variance = pca.explained_variance_ratio_

# Total Explained Variance
total_explained_variance = np.sum(explained_variance)

print("Explained variance:", explained_variance)
print("Total Explained Variance:", total_explained_variance)

10.梯度提升算法

梯度提升是一种先进的机器学习技术。它依次构建多个弱预测模型（通常是决策树）。每个新模型都逐渐最小化整个模型的损失函数（误差）。

评估指标

「对于分类」：准确率、精确率、召回率、F1 分数。
「对于回归」：均方误差 (MSE)、R 平方。

from sklearn.datasets import load_diabetes
from sklearn.ensemble import GradientBoostingRegressor
from sklearn.metrics import mean_squared_error, r2_score

# Load the Diabetes dataset
diabetes = load_diabetes()
X, y = diabetes.data, diabetes.target

# Splitting the dataset into training and testing sets
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2, random_state=42)

# Creating and training the Gradient Boosting model
gb_model = GradientBoostingRegressor(random_state=42)
gb_model.fit(X_train, y_train)

# Predicting the test set results
y_pred_gb = gb_model.predict(X_test)

# Evaluating the model
mse_gb = mean_squared_error(y_test, y_pred_gb)
r2_gb = r2_score(y_test, y_pred_gb)

print("MSE:", mse_gb)