一、基础理论
1. 欧氏距离
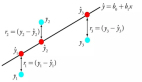
想象你在北京,想要知道离上海有多远,则可以直接计算这个城市(两点)间直线的距离,这就是欧氏距离。
在二维平面上,在二维平面上有两个点A(x1, y1)和B(x2, y2),欧氏距离为:
 图片
图片
欧氏距离衡量的是两点间的真实物理距离,关注的是位置的绝对差异。
2. 曼哈顿距离
想象你在曼哈顿,你想从一个街区走到另外一个街区。你不能走直线,只能沿着街道走,横着走一条街,再竖着走一条街,所行走的路径长度就是曼哈顿距离。
在二维平面上,在二维平面上有两个点A(x1, y1)和B(x2, y2),曼哈顿距离就是:
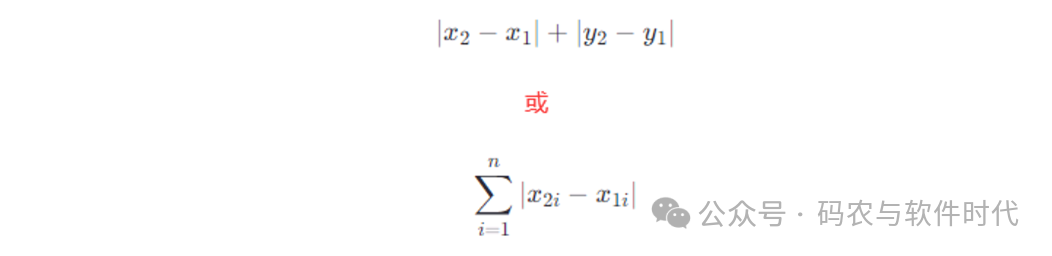 图片
图片
曼哈顿距离考虑的是在各个维度上的绝对差值之和,适用于那些移动只能沿坐标轴进行的情况。
3. 切比雪夫距离
想象你在一个方格化的城市里,每个路口都严格地按照东西南北四个方向排列,就像一个巨大的棋盘。
你现在在一个交叉口,想要去往另一个交叉口,你可以是直行、左转、右转、走对角线(尽管现实中不能这么走),但每次只能走一个街区。
在所有可能的路线中,街区数最大的路线所对应的距离就是切比雪夫距离。
假如在二维平面上有两个点A(x1, y1)和B(x2, y2),切比雪夫距离的公式为:
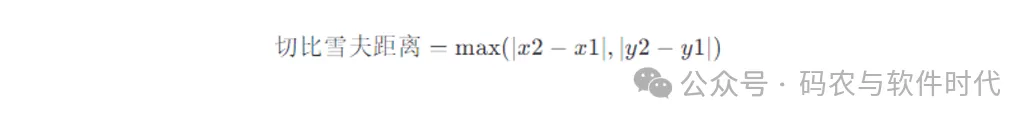
4. 闵可夫斯基距离
假设我们要比较两个点A和B,在n维空间中的坐标分别为
 图片
图片
则闵可夫斯基距离的计算公式是:
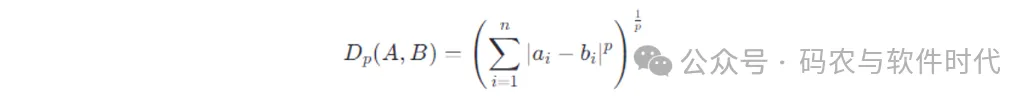 图片
图片
参数𝑝取不同的值时,则就变成了不同的距离:
- 当𝑝=1时,为曼哈顿距离。
- 当𝑝=2时,为欧式距离。
- 当𝑝趋近于无穷大时,为切比雪夫距离。
5. 余弦相似度
余弦相似度是一种衡量两个向量方向相似性的方法。
想象在三维空间有两个向量,一个指向东,另一个指向东北,这两个向量指向角度的接近程度就是余弦相似度。
如果两个向量指向完全相同的方向,相似度为1(即它们的夹角为0度);如果指向完全相反,相似度为-1(180度);如果它们垂直,则相似度为0。
余弦相似度的计算公式:
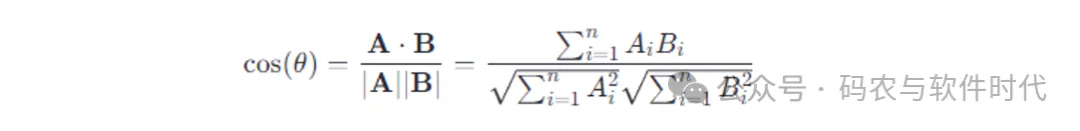 图片
图片
两个向量的点积除以它们各自的长度(模)的乘积。
6. 值差异度量
在讨论距离计算时,特征是要直接比较大小的。
对于连续数值可以直接进行大小比较,如高度、温度、成绩等。
而对于离散特征,又有可以直接比较大小,如教育程度(小学、中学、大学)、服装尺码(S、M、L、XL)等;还有不可以直接比较大小的,如颜色(红、绿、蓝)、国籍(中国、美国、日本)等。
对于不可以直接比较大小的离散特征(离散无序),可以使用值差异度量(Value Difference Metric,VDM)。
VDM的核心思想是离散无序的数据转化为可以量化的差异度量,以进行比较和分析。具体步骤为:
(1)权重分配
A. 频率倒数法:
- 计算频率:对于每个无序特征,统计每个特征值在整个数据集中出现的次数,并计算出频率(出现次数/总样本数)。
- 计算权重:使用频率的倒数或其变形来作为权重。这是因为,频率较高的属性值(即较为常见的值)往往提供较少的区分信息,因此给予较小的权重;反之,频率较低的属性值(罕见值)提供较多区分信息,应给予较高权重。计算公式如 wi=1/fi+ϵ,其中 fi 是特征值i的频率,ϵ 是一个很小的正数(如1e-6),用于防止频率为0时,导致分母为0无法计算的问题。
B. 信息熵或信息增益。
对于两个具体的值 va 和 vb,它们之间的值差异 D(va,vb) 可以直接根据它们的权重 wa 和 wb 计算。如果 va=vb,则差异为0;如果 va不等于vb,差异通常定义为 ∣wa−wb∣。
如果一个样本由多个无序特征组成,比如对象=(特征1,特征2,...,特征𝑛) ,那么可以对每个特征应用上述差异计算方法,然后将所有特征的差异值相加或取平均),以获得两个样本之间的总距离或相似度得分。
假设有一家电商平台想通过分析顾客的购物记录,来发现不同的消费群体。顾客数据包含以下几个无序特征:
(1)性别:男、女。
(2)地区:北京、上海、广州、深圳、其他。
(3)商品类别偏好:电子产品、家居用品、服饰、图书、食品。
VDM计算的过程为:
(1)数据预处理与权重计算
A. 统计频率
- 性别:男(52%),女(48%)
- 地区:北京(25%),上海(29%),广州(18%),深圳(15%),其他(13%)
- 商品类别偏好:电子产品(30%),家居用品(22%),服饰(25%),图书(10%),食品(13%)
B. 计算权重
- 假设采用频率倒数法,加入一个微小常数 ϵ=0.001 。
性别:男(1/0.52 + 0.001)= 1.93, 女(1/0.48 + 0.001)= 2.08。
地区:北京(1/0.25 + 0.001)= 4.04, 上海(1/0.29 + 0.001)= 3.45, 广州(1/0.18 + 0.001)= 5.59, 深圳(1/0.15 + 0.001)= 6.69, 其他(1/0.13 + 0.001)= 7.69。
商品类别偏好:电子产品(1/0.30 + 0.001)= 3.34, 家居用品(1/0.22 + 0.001)= 4.57, 服饰(1/0.25 + 0.001)= 4.04, 图书(1/0.10 + 0.001)= 10.01, 食品(1/0.13 + 0.001)= 7.69。
(2)应用VDM:利用上面计算的权重计算两个顾客间的距离,以进行聚类。
- 假设有两位顾客A和B,A的属性为(男,上海,电子产品),B的属性为(女,北京,图书)。
- 使用VDM计算差异:性别差异 = |1.93 - 2.08| = 0.15;地区差异 = |4.04 - 3.45| = 0.59;商品类别偏好差异 = |3.34 - 10.01| = 6.67。
- 合并差异:总距离 = 0.15 + 0.59 + 6.67 = 7.41。
二、聚类算法
聚类算法是一种无监督学习方法,其主要目的是将一组未标记的数据集分割成多个子集,称为簇(Clusters)。也就是聚类算法并不依赖于预先定义的类别标签,而是通过分析数据本身的特征和结构,自动发现数据中的隐藏模式或群组。
聚类算法的基本思想是基于相似性度量(如欧氏距离、余弦相似性等)来量化数据点之间的相似度,并利用这些度量来优化某个目标函数,从而实现数据的分组。
聚类算法可以根据不同的原则和策略进行分类,主要有:
(1)划分聚类(Partitioning Clustering):将数据集划分为预先指定数量的簇,每个数据点只能属于一个簇。最典型的例子是K-means算法。
(2)层次聚类(Hierarchical Clustering):可以进一步细分为凝聚型(Agglomerative)和分裂型(Divisive)。凝聚型算法从每个数据点作为一个独立的簇开始,然后逐步合并最相似的簇,直到满足某个终止条件;而分裂型则相反,开始时将所有数据视为一个簇,然后逐渐分裂。常见的算法有AGNES(Agglomerative Nesting)、DIANA(Divisive Analysis)、BIRCH等。
(3)基于密度的聚类(Density-Based Clustering):基于数据点的邻域密度来确定簇,能够处理形状不规则的簇和含有噪声的数据。DBSCAN(Density-Based Spatial Clustering of Applications with Noise)是最知名的算法之一,它通过设置邻域半径和最小点数来识别高密度区域。OPTICS、DENCLUE也是基于密度的算法。
(4)基于网格的聚类(Grid-Based Clustering):将数据空间划分为多个单元或网格,然后在网格层次上进行聚类。STING(Statistical Information Grid-based Clustering)、WaveCluster、CLIQUE(Clustering in Quest)是典型代表,它们适合处理大规模空间数据库。
(5)基于模型的聚类(Model-Based Clustering):假设数据由某些数学模型(如高斯分布)生成,并尝试找到最佳的模型参数来描述数据。高斯混合模型(GMM, Gaussian Mixture Model)是最常见的例子,它通过最大似然估计来拟合数据到多个高斯分布上。
三、K-means算法
K-means算法是一种将数据集划分为K个互不相交的子集(簇),使得同一簇内的数据点彼此相似,而不同簇的数据点相异。
K-means(均值)算法的基本操作过程为:
1. 初始设置
(1)数据集:假设我们有一个二维数据集,包含以下五个数据点:{X(1, 2), Y(2, 1), Z(4, 8), W(5, 9), V(6, 7)}。
(2)初始化质心:随机选择两个数据点作为初始聚类中心(质心):C1(2, 3), C2(6, 7)。
2. 执行步骤
步骤1: 数据点分配
- 对于数据集中的每个数据点,计算到C1和C2的距离。
 图片
图片
- 将每个数据点分配给距离最近的质心所在的簇。
假设结果为:
C1簇: {X(1, 2), Y(2, 1)}
C2簇: {Z(4, 8), W(5, 9), V(6, 7)}
步骤2: 更新质心
 图片
图片
步骤3: 迭代与收敛判断
- 重复步骤1和步骤2,直到质心的移动距离小于某个预设的阈值或达到预定的迭代次数。这一步确保算法收敛于一个稳定的聚类结果。
需要注意的是:
(1)初始质心选择:K-means算法对初始质心的选择敏感,不同的初始质心可能导致不同的聚类结果。
(2)簇形状:K-means假设簇为凸形状,可能不适合处理复杂的数据分布,如密度不均或存在异常点的情况。
(3)K值选择:选择合适的K值是关键,常用方法有肘部法则(Elbow Method)和轮廓系数法等。