预测中的不确定性对于决策者了解潜在结果和相关风险的范围非常重要。通过量化不确定性，企业可以做出更明智的决策，并有效地分配资源。关于预测的不确定性，前面有"用于时间序列概率预测的定量回归“ 和 ”时间序列概率预测的共形预测“的介绍。本文将介绍另一项重要技术--共形分位数回归（CQR）。共形分位数回归（CQR）结合了分位数回归（QR）和共形预测（CP），使两者相辅相成。
分位数回归 QR
QR 估算的是目标变量的条件量值，如中位数或第 90 个百分位数，而不是条件均值。通过分别估计不同水平预测变量的条件量值，可以很好地处理异方差。虽然大多数情况下量化值可以提供准确的预测区间，但当模型假设被违反时，量化值预测可能会不准确。
共形预测 CP
另一方面，CP 能确保预测区间中的实际值，而无需明确关注特定的量化值。它根据实际数据而非任何模型规范形成预测区间。对所有数据范围都会产生一个固定的宽度。
共形分位数回归CQR
为什么不同时使用 QR 和 CP 呢？共形分位数回归（CQR）技术提供了一个值得称赞的解决方案，可以提供具有有效覆盖保证的预测区间。这些覆盖保证是由量回归产生的。CQR 调整了预测区间，以确保实际值总是落在预测区间内，并达到所需的置信水平。
什么是CQR
CQR（Conformal Quantile Regression）的基本思想是建立分位数回归（QR）模型用于预测区间，并使用CP技术进行调整。上一章中介绍了CP如何建立预测区间，通过获取点预测值与实际值之间的误差得出容差区间，然后将其与点估计值相连形成预测区间。然而，QR已经给出了预测区间。要调整预测区间，我们需要修改CP方法为CQR，因为在量化预测中，CP以点预测为中心，而应用于预测区间的CQR则以预测区间的两个锚点（下限和上限）为中心。
CQR的发展过程称为一致性得分。符合性得分涉及实际值与预测区间上下限之间的距离。如果实际值持续高于上限或下限，则应根据一致性得分调整预测区间，确保在选定的时间水平下，实际值在预测区间内。一致性得分是大括号中两个项中较大的一项。
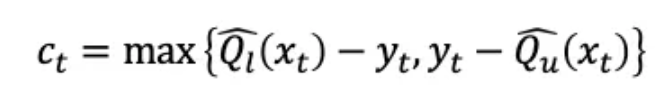公式（1）
其中，yt是实际值，Ql和Qu是低量化值和高量化值（下限和上限），ct是符合性得分
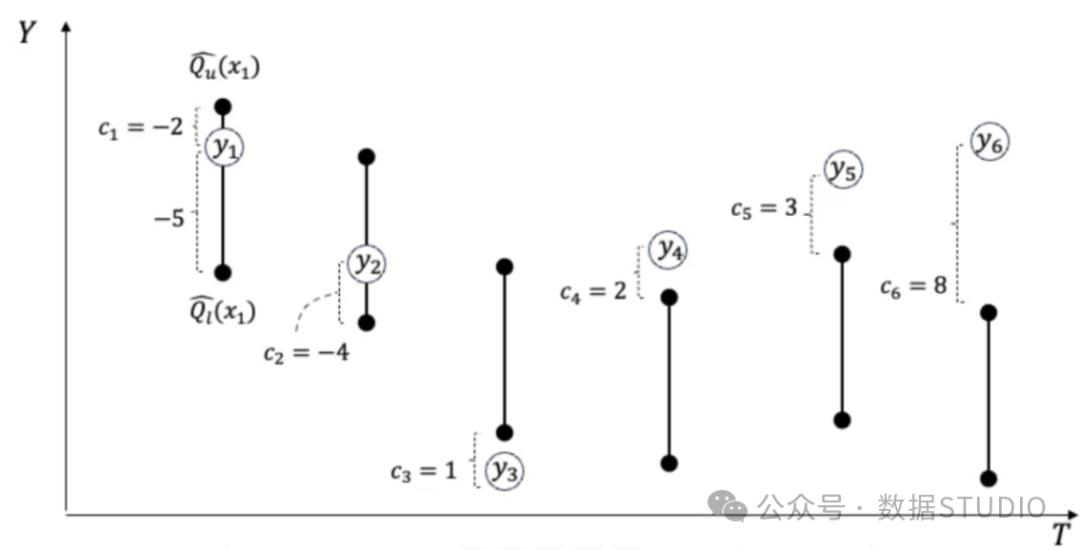
我们以图(A)中的示例来解释等式(1)。假设有六个实际值y1至y6及其相应的预测区间。在第一次预测中，实际值y1的预测区间在下限Ql和上限Qu之间，而y1更接近上限QU。每个预测区间都会有一个一致性得分。根据公式(1)，第一个预测值c1的一致性分值为-2，处于-2和-5之间。当y在预测区间内时，一致性总是负数，而当实际值在预测区间外时，一致性总是正数。
图(A)：一致性得分
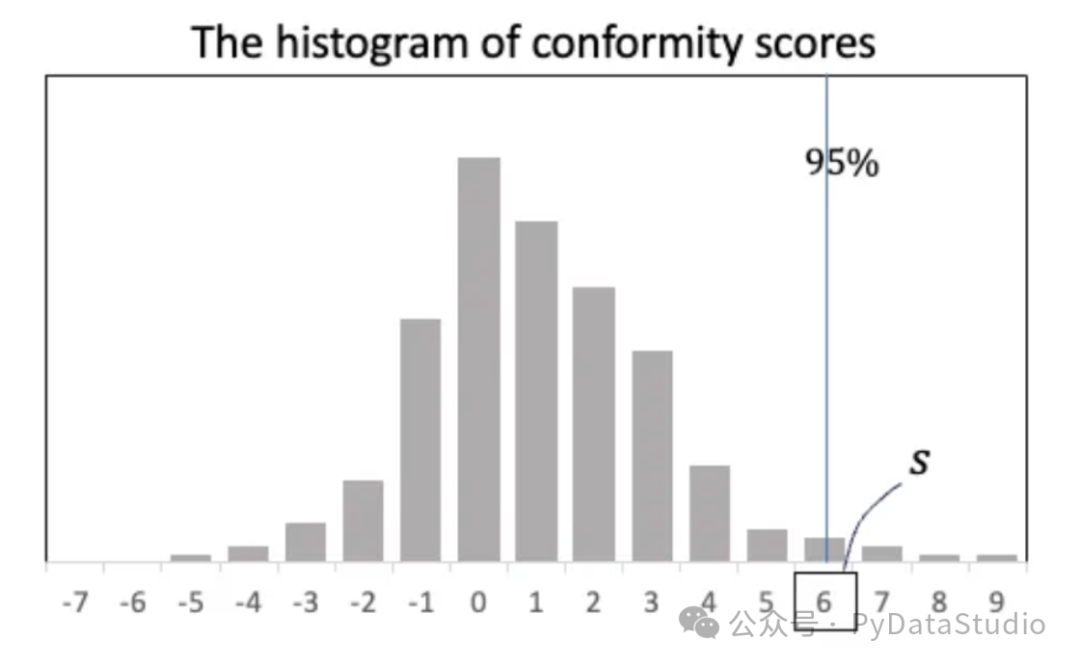
我们将为一致性得分绘制一个直方图，如图（B）所示。左侧的负分表示实际值在预测区间内。右侧的正分数表示预测区间无法捕捉实际值。
图(B)：一致性得分直方图
可以根据容忍度确定一个阈值s。根据图(B)，95% 一致性得分是 6.0。预测区间将会扩大，保证实际值包含在预测区间内。
形式上，CQR 根据下面的公式 (2) 调整分位数回归的预测区间。它从下限Ql中减去阈值s，再将阈值s加到上限QU：
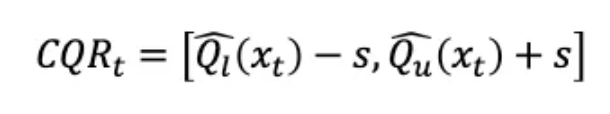公式（2）
一致性得分可为负，表示所有预测区间均包含实际值。在这种情况下，符合性得分的加减可能导致预测区间变短。CQR 会根据 QR 在区间内的表现调整预测区间，对于始终低估或高估的 QR 会做出相应调整。
CQR 的构建
其过程可概括如下：
- 首先，我们将历史时间序列数据分为训练期、校准期和测试期。
- 然后在训练数据上训练分位数回归模型。应用训练模型生成校准数据的量化预测。
- 然后根据公式 (1) 计算一致性得分。绘制符合性得分直方图，以定义容差水平，如图 (B)。
- 然后根据公式 (2) 调整不同量化值的预测区间。
环境要求
NeuralProphet 有三个选项：(i) 分位数回归 (QR)(ii) 保形预测 (CP)(iii) 保形分位数回归 (CQR)，用于处理预测的不确定性。
!pip install neuralprophet
!pip uninstall numpy
!pip install git+https://github.com/ourownstory/neural_prophet.git numpy==1.23.5数据
%matplotlib inline
from matplotlib import pyplot as plt
import pandas as pd
import numpy as np
import logging
import warnings
logging.getLogger('prophet').setLevel(logging.ERROR)
warnings.filterwarnings("ignore")
data = pd.read_csv('/bike_sharing_daily.csv')
# 数据获取：公众号：数据STUDIO 后台回复 云朵君
data.tail()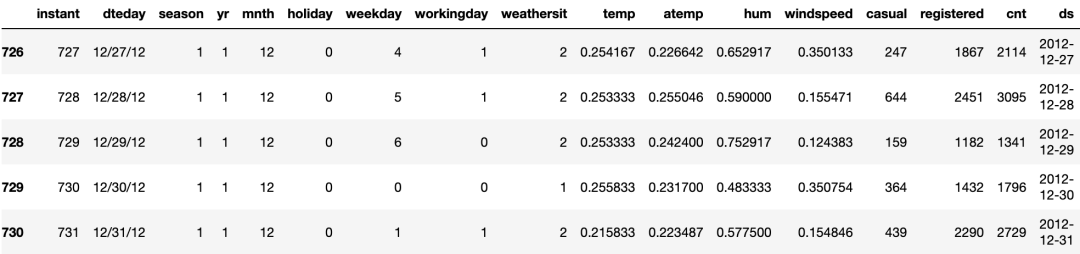
图(C)：自行车租赁数据
数据集包含每日租赁需求、天气信息（如温度和风速）等多变量数据。在进行建模之前，需要对数据进行最基本的准备。NeuralProphet 要求列名为ds和y。
# convert string to datetime64
data["ds"] = pd.to_datetime(data["dteday"])
df = data[['ds','cnt']]
df.columns = ['ds','y']建模
使用具有趋势和季节性模式的NeuralProphet模型，可以添加其他组件，如AR、假期和其他协变量。目前代码已进行了注释。
from neuralprophet import NeuralProphet
quantile_list=[0.05,0.95 ]
# Model and prediction
cqr_model = NeuralProphet(
quantiles=quantile_list,
#n_changepoints=10,
yearly_seasnotallow=True,
weekly_seasnotallow=True,
daily_seasnotallow=False,
# Add the autogression
#n_lags=10,
# Forecast the next 50 days
#n_forecasts= 50
)
cqr_model = cqr_model.add_country_holidays("US")
#cqr_model.set_plotting_backend("matplotlib") # Use matplotlib训练、验证和测试数据
共形分位数回归的一个关键步骤是将训练数据分为训练数据和校准数据，用于构建符合性得分。
df_train, df_test = cqr_model.split_df(df, valid_p=0.2)
df_train, df_cal = cqr_model.split_df(df_train, freq="D", valid_p=1.0 / 11)
[df_train.shape, df_test.shape, df_cal.shape]
# [(532, 2), (146, 2), (53, 2)]用三种颜色绘制不同的数据集。
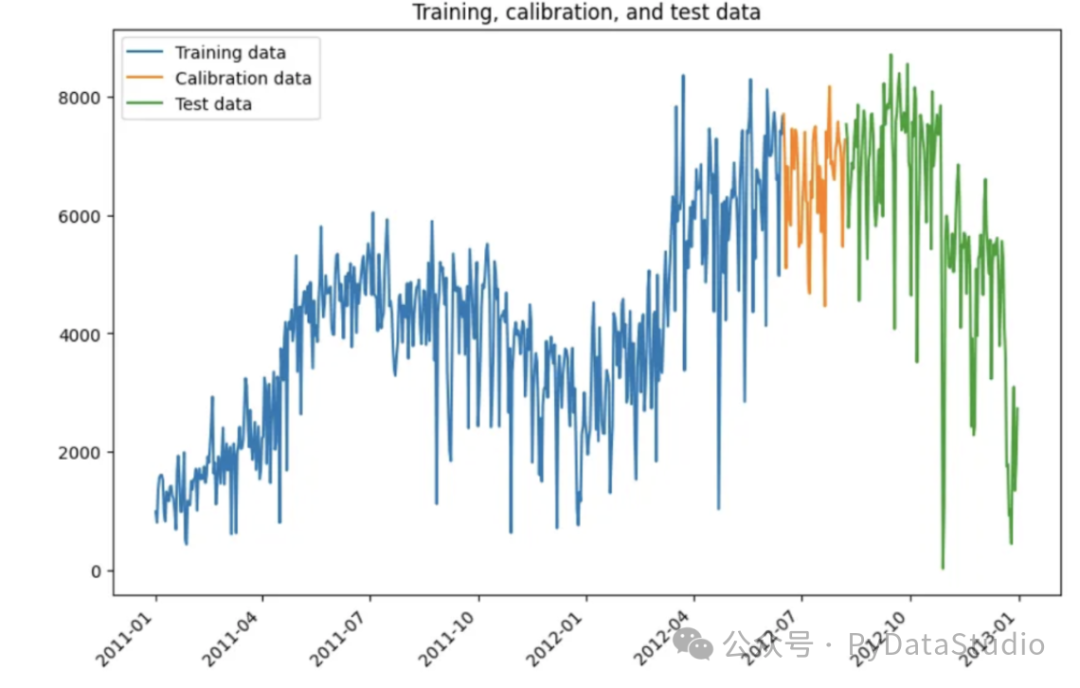图（D）
验证数据作为模型验证集。
metrics = cpr_model.fit(df_train, validation_df=df_cal, progress="bar")
metrics.tail()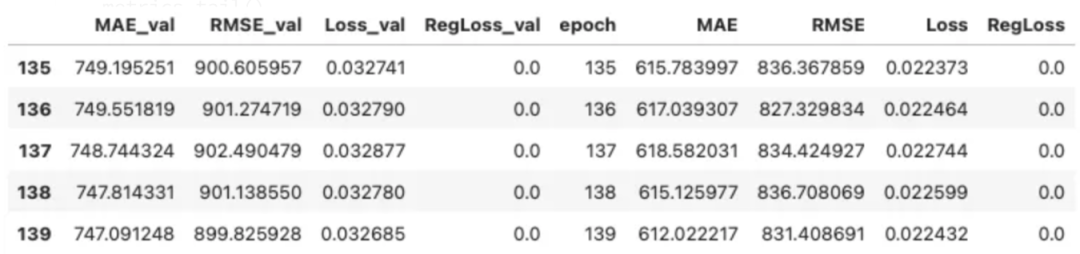
图片
共形分位数回归
创建一个future数据集，在df数据的最后日期之后有50个周期。它将包括所有历史数据的模型预测。或者，如果指定n_historic_predictinotallow=40，它将只包含40个历史数据点及其预测结果。
NeuralProphet 的 CQR 选项是method=cqr。我们将通过.conformal_prediction()启用保形预测。
future = cpr_model.make_future_dataframe(df, periods=50,
n_historic_predictinotallow=True)
# Parameter for CQR
method = "cqr"
alpha = 0.05
# Enable conformal prediction on the pre-trained models
cqr_forecast = cqr_model.conformal_predict(
# df_test, # You can also use df_test
future,
calibration_df=df_cal,
alpha=alpha,
method=method,
show_all_PI=True,
)
cqr_forecast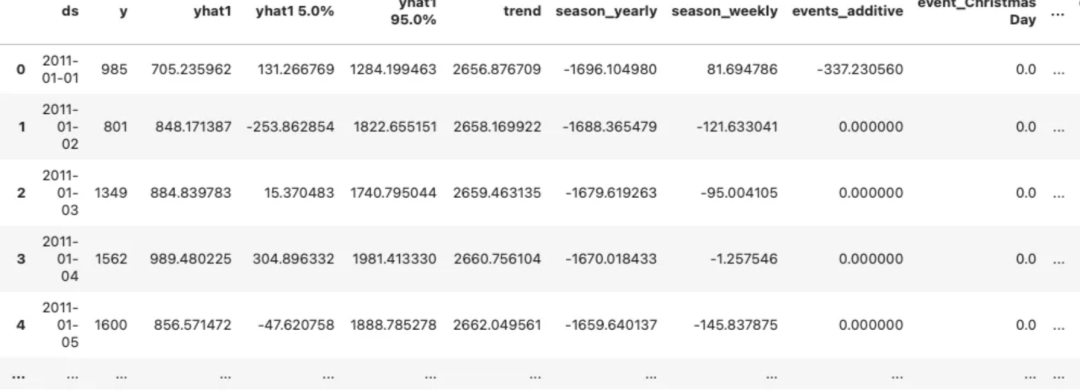
图片
绘制预测结果和预测区间图。CQR 预测区间宽度变化。在图（E）中，95% 的情况下，实际值都在预测区间内，因为 CP 可以确保实际值在预测区间内的时间为95%。
fig = cqr_model.plot(cqr_forecast,
#plotting_backend = "matplotlib"
plotting_backend="plotly-static"
)
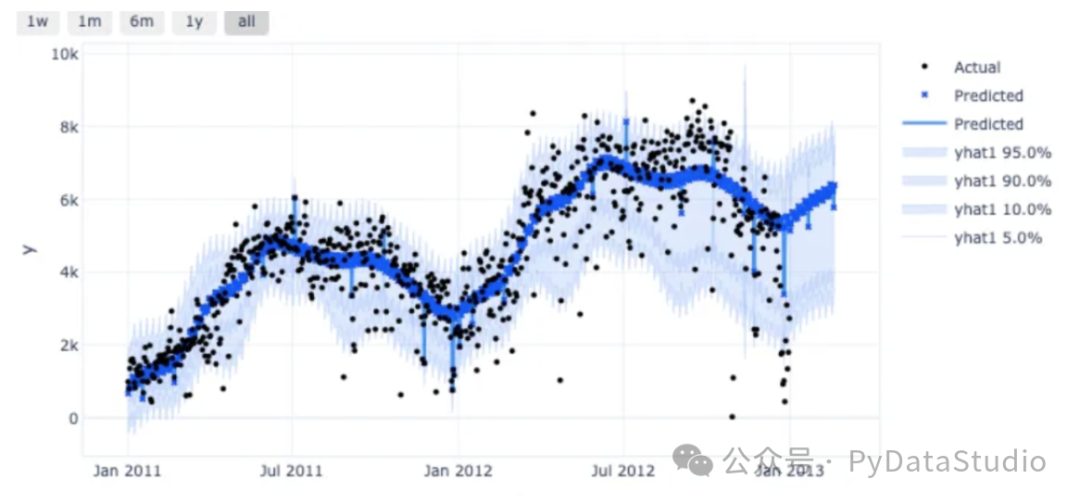图（E）
