时间序列概率预测的共形预测-51CTO.COM

前面我们介绍了用于时间序列概率预测的分位数回归，今天继续学习基于概率预测的时间序列概率预测方法--共形预测。

现实世界中的应用和规划往往需要概率预测，而不是简单的点估计值。概率预测也称为预测区间或预测不确定性，能够提供决策者对未来的不确定性状况有更好的认知。传统的机器学习模型如线性回归、随机森林或梯度提升机等，旨在产生单一的平均估计值，而无法直接给出可能结果的数值范围。如何从点估计扩展到预测区间，正是现代时间序列建模技术所关注的重点。

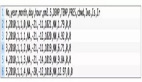
在预测建模中，我们知道模型的目标是为条件均值给出无偏估计。估计值与实际样本值之间的差距被称为误差，体现了模型的不确定性。那么，如何量化这种不确定性呢?由于误差代表了估计值与实际值之间的偏差，因此我们可以通过分析误差的分布来量化不确定性的程度。

共形预测(Conformal Prediction，CP)正是一种基于这一思路的预测方法。它利用历史数据，根据新的预测样本点在已知误差分布中的位置，为这个新预测给出一个范围估计，使其以期望的置信度(如95%)落入此范围内。值得注意的是，CP是一种与具体模型无关的元算法，可以应用于任何机器学习模型，从而将点估计扩展到概率预测区间。

概率预测的优势在于，它不仅给出预测的平均水平，还能提供相应的不确定性量化信息。这种额外的不确定性信息对风险管理、决策优化等应用场景至关重要。比如在供应链、库存管理等领域，通过概率预测可以权衡需求波动的风险，制定更加鲁棒的规划策略。

什么是共形预测

Conformal Prediction是一种非参数方法，用于生成具有概率保证的预测区域。它不依赖于特定的概率分布假设，而是通过计算数据点的“相似性”或“一致性”来产生预测。这种方法可以应用于各种类型的输入数据（如连续变量、分类标签、时间序列等）和输出（如回归、分类、排序等）。

技术分析

该项目实现了一套Python库，包含多种算法，如Inference for Regression, Multi-class Classification等，以支持Conformal Prediction的应用。关键步骤包括：

训练集准备：首先，对数据进行预处理，并将其分为训练集和验证集。
构建基础模型：利用训练集训练一个基础预测模型（如线性回归、决策树或神经网络）。
计算非conformity分数：对于每个验证集样本，使用模型生成预测，并计算其与实际观测值的非conformity分数。
确定阈值：通过将这些非conformity分数排序并应用α-level，确定划分预测区间的阈值。
预测阶段：对于新的未标记数据，根据该阈值生成预测区间。

这种框架允许用户在保持预测性能的同时，为预测误差提供严格的概率保证。

应用场景

金融风险评估：在信贷评分中，可以预测未来的违约概率，并给出置信区间，帮助金融机构做出更稳健的决策。
医学诊断：在医疗预测中，可以估计治疗效果的范围，为医生提供更全面的信息。
市场趋势预测：在商业环境中，可以预测销售量或股票价格，为策略制定者提供可靠参考。

特点

灵活性：适用于不同类型的预测问题和数据类型。
可解释性：提供的预测区间有助于理解模型的不确定性。
无假设：不需要对数据的底层分布做假设，增强了泛化能力。
概率保证：可以量化错误率，提高预测的可靠性。

共形回归(Conformal Regression)是一种获得预测区间的有效方法，其构造过程可以概括为以下几个步骤:

计算误差分布首先计算历史数据中每个样本点的预测误差，即预测值与真实值之间的绝对差值。然后将这些误差值从小到大排序。
确定误差临界值在排序后的误差分布中，选取一个临界值，使得小于等于该临界值的误差所占比例等于期望的置信度(如95%)。该临界值被视为可接受的最大预测误差。
构建预测区间对于新的预测样本点，其预测区间被设定为[预测值-误差临界值，预测值+误差临界值]。根据误差临界值的选取，该预测区间能以期望的置信度(如95%)包含真实值。

共形回归的优势在于，它是一种与具体模型无关的元算法，可以应用于任何机器学习回归模型的结果之上，从点估计扩展到概率预测区间。其关键是利用历史误差分布来量化新预测的不确定性，为决策过程提供了更多不确定性信息。

需要指出的是，共形回归所构建的预测区间是保守的，其宽度会随着置信度的提高而增加。在一些对过度保守不利的应用场景中，可以考虑引入其他校正方法来缩小区间宽度。另一方面，共形技术还可以推广到分类、异常检测等其他机器学习任务。

共形预测的构造

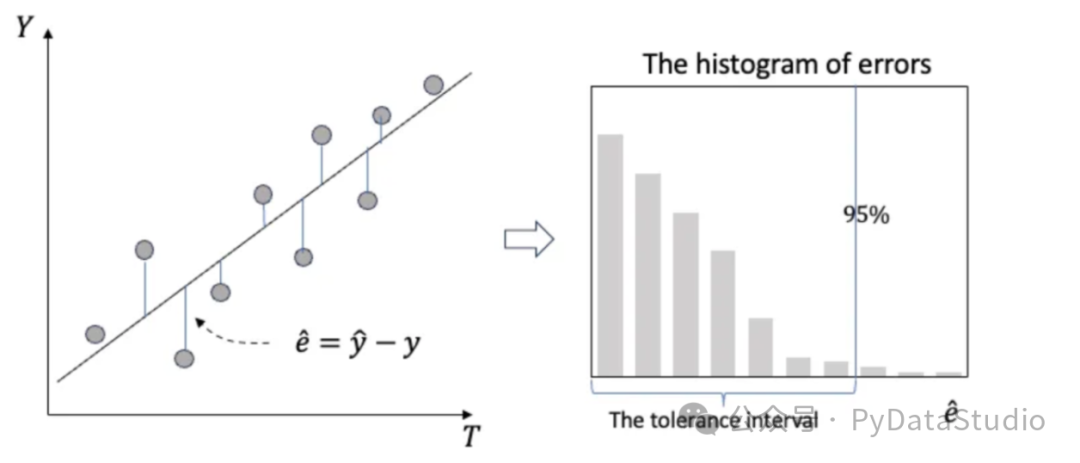
这是在寻找预测区间的程序中使用的共形预测（CP）策略。请注意，它对模型规格和基础数据分布不做任何假设。CP 与模型无关--适用于任何建模技术。共形预测技术由 Volodya Vovk、Alexander Gammerman 和 Craig Saunders（1999 年）以及 Harris Papadopoulos、Kostas Proedrou、Volodya Vovk 和 Alex Gammerman（2002 年）提出。共形预测算法的工作原理如下：

将历史时间序列数据分为训练期、校准期和测试期。
在训练数据上训练模型。
使用训练好的模型对校准数据进行预测。然后绘制预测误差直方图，并定义如图 (A) 所示的容差水平。
将容差区间加减到任何未来点估算中，包括测试数据中的预测，以提供预测区间。

环境要求

在预测区间上，NeuralProphet 有三种选择：(i) 分位数回归 (QR)(ii) 共形预测 (CP)(iii) 共形分位数回归 (CQR)。

你将按照标准安装程序 pip install NeuralProphet 来安装 NeuralProphet。

!pip install neuralprophet
!pip uninstall numpy
!pip install git+https://github.com/ourownstory/neural_prophet.git numpy==1.23.5

数据

这里我们将直接加载数据。这里的数据集可以直接在公众号：数据STUDIO 里搜索开源 23 个优秀的机器学习数据集，这里有提供。

%matplotlib inline
from matplotlib import pyplot as plt
import pandas as pd
import numpy as np
import logging
import warnings
logging.getLogger('prophet').setLevel(logging.ERROR)
warnings.filterwarnings("ignore")
# 数据获取：在公众号：数据STUDIO 后台回复 云朵君
data = pd.read_csv('/bike_sharing_daily.csv')
data.tail()

自行车租赁数据

这个数据集包含多变量数据，每天的租赁需求和其他天气信息（如温度和风速）。我们需要做最基本的数据准备来进行建模。NeuralProphet 要求列名为 ds 和 y。

# convert string to datetime64
data["ds"] = pd.to_datetime(data["dteday"])
df = data[['ds','cnt']]
df.columns = ['ds','y']

建模

使用一个简单的 NeuralProphet 模型，包括趋势和季节性模式，也可以加入其他成分，如 AR、假期和其他协变量。

from neuralprophet import NeuralProphet, set_log_level
cp_model = NeuralProphet(
    yearly_seasnotallow=True,
    weekly_seasnotallow=True,
    daily_seasnotallow=False,
)
cp_model.set_plotting_backend("plotly-static")

训练、验证和测试数据

共形预测或共形分位数回归技术的一个重要的步骤是将训练数据分为训练数据和验证数据，验证数据将用于构建容差统计。

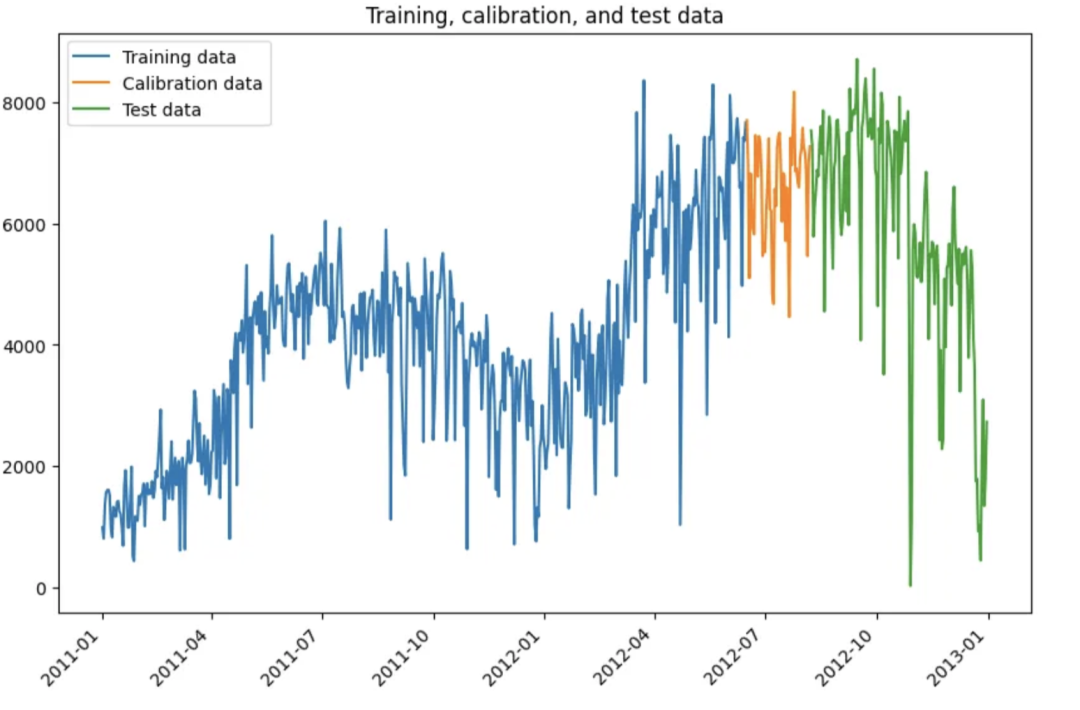
df_train, df_test = cp_model.split_df(df, valid_p=0.2)
df_train, df_cal = cp_model.split_df(df_train, freq="D", valid_p=1.0 / 11)
[df_train.shape, df_test.shape, df_cal.shape]
# [(532, 2), (146, 2), (53, 2)]

我们用三种颜色绘制数据子集。

图片

我们使用验证数据作为模型验证集。

metrics = cp_model.fit(df_train, validation_df=df_cal, progress="bar")
metrics.tail()

图片

然后，我们就可以进行预测并附加预测区间了。虽然 NeuralProphet 可以自动完成 CP，但我们还是要手动操作，以便向您展示操作步骤。

共形预测

我们计划创建一个future数据集，该数据集将在df数据的最后日期之后延续 50 个周期。该数据集将包含模型对所有历史数据的预测，或者如果我们设定n_historic_predictinotallow=40，则将仅包括 40 个历史数据点及其预测结果。

NeuralProphet 的 CP 选项是 method=naive。我们将通过 .conformal_prediction()启用保形预测。

future = cp_model.make_future_dataframe(df, periods=50, 
     n_historic_predictinotallow=True)

# Parameter for naive conformal prediction
method = "naive"
alpha = 0.05

# Enable conformal prediction on the pre-trained models
cp_forecast = cp_model.conformal_predict(
    # df_test, # You can also use df_test
    future,
    calibration_df=df_cal,
    alpha=alpha,
    method=method,
    show_all_PI=True,
)
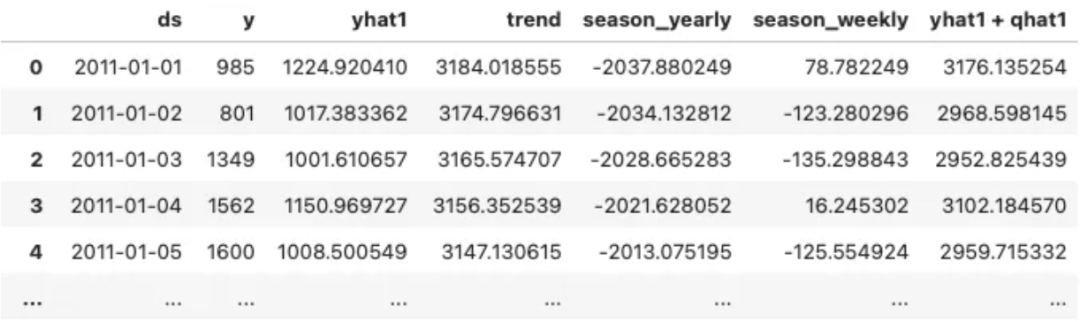
cp_forecast

输出包含预测值 yhat1 和上限 yhat1 + qhat1。qhat1 是根据校准数据得出的容差范围。

图片

从 yhat1+qhat1中减去 yhat1即可得到 qhat1。这是一个 1951.214 的单一值。然后，我们可以通过从 yhat1减去 qhat1 得出下限。

cp_forecast['qhat1'] = cp_forecast['yhat1 + qhat1'] - cp_forecast['yhat1'] 
cp_forecast['yhat1 - qhat1'] = cp_forecast['yhat1'] - cp_forecast['qhat1']
cp_forecast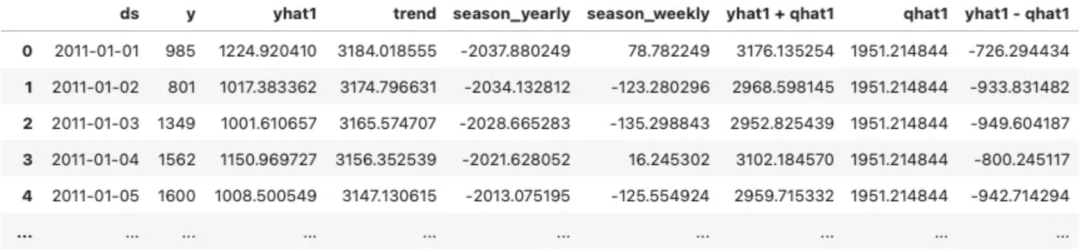

绘制预测值和预测区间图。你会发现CP一直是一个固定值，在所有时段都是如此。它与预测值相加或相减得出上下限。

import matplotlib.pyplot as plt
plt.figure(figsize=(10,6))
#plot each series
plt.plot(df_train['ds'],df_train['y'], label='Training data')
plt.plot(df_cal['ds'],df_cal['y'], label='Calibration data')
plt.plot(df_test['ds'],df_test['y'], label='Test data')

plt.plot(cp_forecast['ds'],cp_forecast['yhat1'], label='Prediction')
plt.plot(cp_forecast['ds'],cp_forecast['yhat1 - qhat1'], label='Lower bound')
plt.plot(cp_forecast['ds'],cp_forecast['yhat1 + qhat1'], label='Upper bound')
plt.legend()
plt.title('Conformal prediction')
plt.xticks(rotatinotallow=45, ha='right')
# Draw a vertical dashed line
plt.axvline(x=df_test['ds'].tail(1), color='r', linestyle='--', linewidth=2) 
plt.show()

共形预测

公差区间是根据校准数据中的实际值得出的。

结论

本文介绍了共形预测技术，提供预测区间。共形预测的构造不依赖于任何模型假设，可适用于任何模型。此外，我们展示了在NeuralProphet中构建预测区间的代码示例。一些人可能已经注意到，预测区间在所有时间段都是相同长度的。在某些情况下，不同的预测间隔可能更有意义。