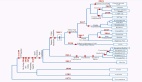
多层感知器(MLP),也被称为全连接前馈神经网络,是当今深度学习模型的基础构建块。MLP 的重要性无论怎样强调都不为过,因为它们是机器学习中用于逼近非线性函数的默认方法。
但是最近,来自 MIT 等机构的研究者提出了一种非常有潜力的替代方法 ——KAN。该方法在准确性和可解释性方面表现优于 MLP。而且,它能以非常少的参数量胜过以更大参数量运行的 MLP。比如,作者表示,他们用 KAN 重新发现了结理论中的数学规律,以更小的网络和更高的自动化程度重现了 DeepMind 的结果。具体来说,DeepMind 的 MLP 有大约 300000 个参数,而 KAN 只有大约 200 个参数。
这些惊人的结果让 KAN 迅速走红,吸引了很多人对其展开研究。很快,有人提出了一些质疑。其中,一篇标题为《KAN is just MLP》的 Colab 文档成为了议论的焦点。
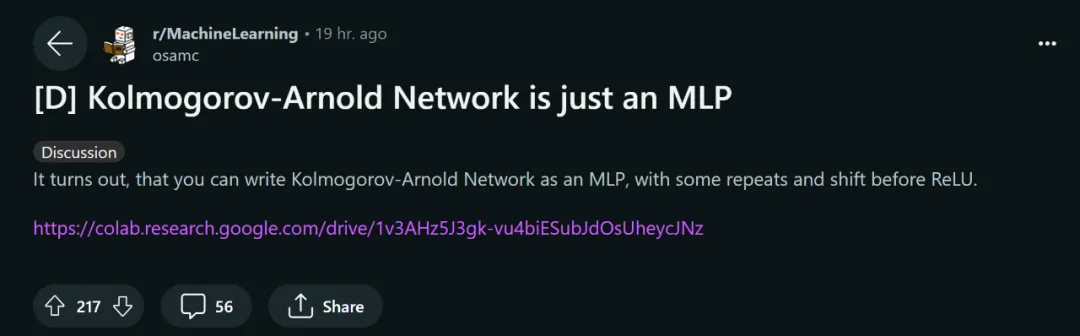
KAN 只是一个普通的 MLP?
上述文档的作者表示,你可以把 KAN 写成一个 MLP,只要在 ReLU 之前加一些重复和移位。
在一个简短的例子中,作者展示了如何将 KAN 网络改写为具有相同数量参数的、有轻微的非典型结构的普通 MLP。
需要记住的是,KAN 在边上有激活函数。它们使用 B - 样条。在展示的例子中,为了简单起见,作者将只使用 piece-wise 线性函数。这不会改变网络的建模能力。
下面是 piece-wise 线性函数的一个例子:
def f(x):
if x < 0:
return -2*x
if x < 1:
return -0.5*x
return 2*x - 2.5
X = torch.linspace(-2, 2, 100)
plt.plot(X, [f(x) for x in X])
plt.grid()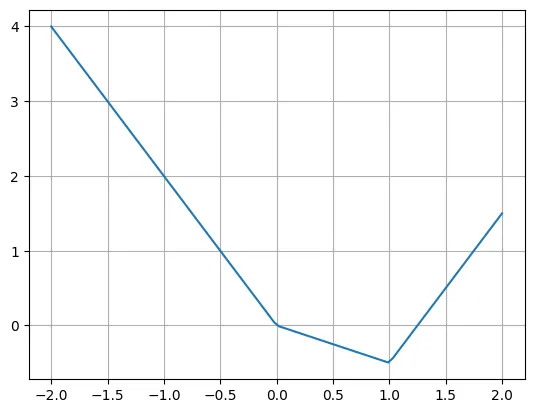
作者表示,我们可以使用多个 ReLU 和线性函数轻松重写这个函数。请注意,有时需要移动 ReLU 的输入。
plt.plot(X, -2*X + torch.relu(X)*1.5 + torch.relu(X-1)*2.5)
plt.grid()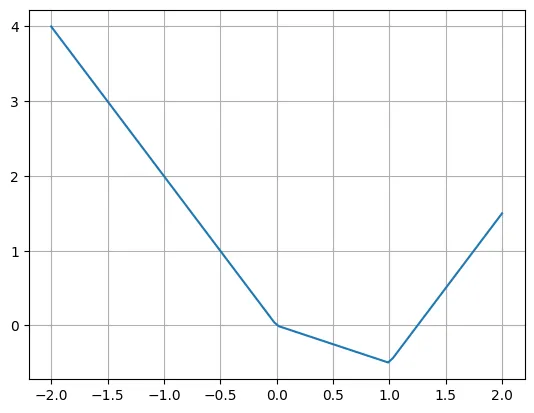
真正的问题是如何将 KAN 层改写成典型的 MLP 层。假设有 n 个输入神经元,m 个输出神经元,piece-wise 函数有 k 个 piece。这需要 n∗m∗k 个参数(每条边有 k 个参数,而你有 n∗m 条边)。
现在考虑一个 KAN 边。为此,需要将输入复制 k 次,每个副本移动一个常数,然后通过 ReLU 和线性层(第一层除外)运行。从图形上看是这样的(C 是常数,W 是权重):
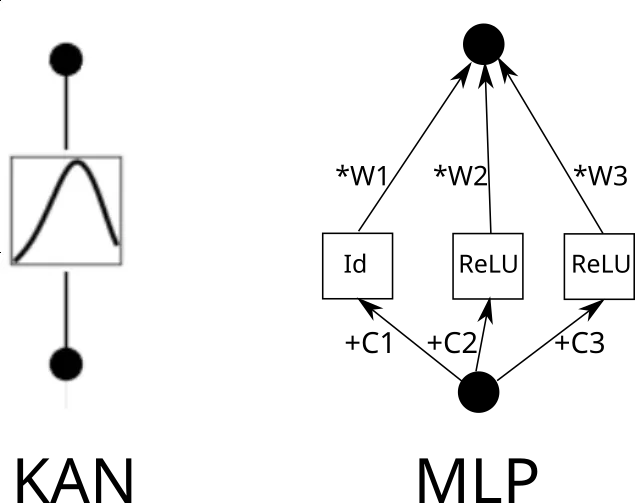
现在,可以对每一条边重复这一过程。但要注意一点,如果各处的 piece-wise 线性函数网格相同,我们就可以共享中间的 ReLU 输出,只需在其上混合权重即可。就像这样:
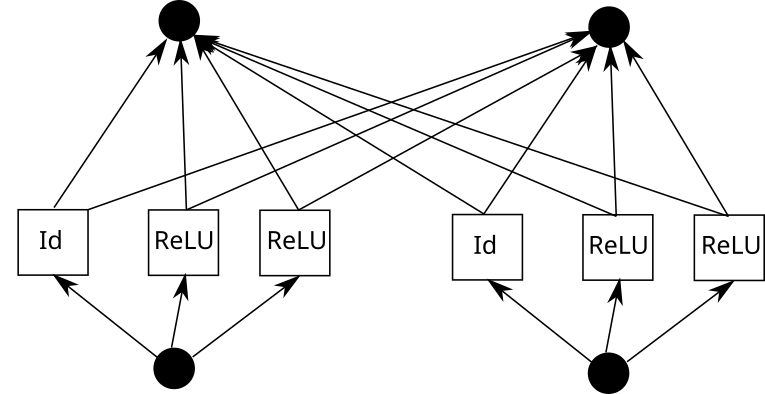
在 Pytorch 中,这可以翻译成以下内容:
k = 3 # Grid size
inp_size = 5
out_size = 7
batch_size = 10
X = torch.randn(batch_size, inp_size) # Our input
linear = nn.Linear(inp_size*k, out_size) # Weights
repeated = X.unsqueeze(1).repeat(1,k,1)
shifts = torch.linspace(-1, 1, k).reshape(1,k,1)
shifted = repeated + shifts
intermediate = torch.cat([shifted[:,:1,:], torch.relu(shifted[:,1:,:])], dim=1).flatten(1)
outputs = linear(intermediate)现在我们的层看起来是这样的:
- Expand + shift + ReLU
- Linear
一个接一个地考虑三个层:
- Expand + shift + ReLU (第 1 层从这里开始)
- Linear
- Expand + shift + ReLU (第 2 层从这里开始)
- Linear
- Expand + shift + ReLU (第 3 层从这里开始)
- Linear
忽略输入 expansion,我们可以重新排列:
- Linear (第 1 层从这里开始)
- Expand + shift + ReLU
- Linear (第 2 层从这里开始)
- Expand + shift + ReLU
如下的层基本上可以称为 MLP。你也可以把线性层做大,去掉 expand 和 shift,获得更好的建模能力(尽管需要付出更高的参数代价)。
- Linear (第 2 层从这里开始)
- Expand + shift + ReLU
通过这个例子,作者表明,KAN 就是一种 MLP。这一说法引发了大家对两类方法的重新思考。

对 KAN 思路、方法、结果的重新审视
其实,除了与 MLP 理不清的关系,KAN 还受到了其他许多方面的质疑。
总结下来,研究者们的讨论主要集中在如下几点。
第一,KAN 的主要贡献在于可解释性,而不在于扩展速度、准确性等部分。
论文作者曾经表示:
- KAN 的扩展速度比 MLP 更快。KAN 比参数较少的 MLP 具有更好的准确性。
- KAN 可以直观地可视化。KAN 提供了 MLP 无法提供的可解释性和交互性。我们可以使用 KAN 潜在地发现新的科学定律。
其中,网络的可解释性对于模型解决现实问题的重要性不言而喻:

但问题在于:「我认为他们的主张只是它学得更快并且具有可解释性,而不是其他东西。如果 KAN 的参数比等效的 NN 少得多,则前者是有意义的。我仍然感觉训练 KAN 非常不稳定。」

那么 KAN 究竟能不能做到参数比等效的 NN 少很多呢?
这种说法目前还存在疑问。在论文中,KAN 的作者表示,他们仅用 200 个参数的 KAN,就能复现 DeepMind 用 30 万参数的 MLP 发现数学定理研究。在看到该结果后,佐治亚理工副教授 Humphrey Shi 的两位学生重新审视了 DeepMind 的实验,发现只需 122 个参数,DeepMind 的 MLP 就能媲美 KAN 81.6% 的准确率。而且,他们没有对 DeepMind 代码进行任何重大修改。为了实现这个结果,他们只减小了网络大小,使用随机种子,并增加了训练时间。

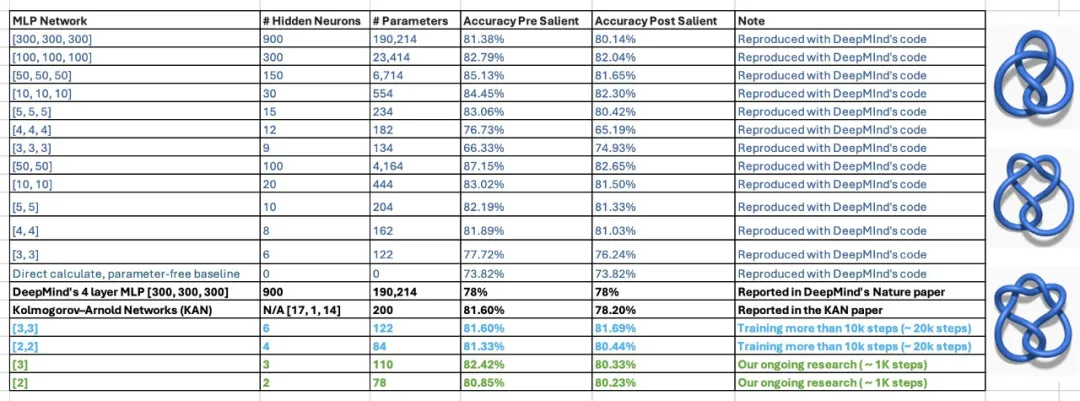
对此,论文作者也给出了积极的回应:
第二,KAN 和 MLP 从方法上没有本质不同。

「是的,这显然是一回事。他们在 KAN 中先做激活,然后再做线性组合,而在 MLP 中先做线性组合,然后再做激活。将其放大,基本上就是一回事。据我所知,使用 KAN 的主要原因是可解释性和符号回归。」
除了对方法的质疑之外,研究者还呼吁对这篇论文的评价回归理性:
「我认为人们需要停止将 KAN 论文视为深度学习基本单元的巨大转变,而只是将其视为一篇关于深度学习可解释性的好论文。在每条边上学习到的非线性函数的可解释性是这篇论文的主要贡献。」
第三,有研究者表示,KAN 的思路并不新奇。
「人们在 20 世纪 80 年代对此进行了研究。Hacker News 的讨论中提到了一篇意大利论文讨论过这个问题。所以这根本不是什么新鲜事。40 年过去了,这只是一些要么回来了,要么被拒绝的东西被重新审视的东西。」
但可以看到的是,KAN 论文的作者也没有掩盖这一问题。
「这些想法并不新鲜,但我不认为作者回避了这一点。他只是把所有东西都很好地打包起来,并对 toy 数据进行了一些很好的实验。但这也是一种贡献。」
与此同时,Ian Goodfellow、Yoshua Bengio 十多年前的论文 MaxOut(https://arxiv.org/pdf/1302.4389)也被提到,一些研究者认为二者「虽然略有不同,但想法有点相似」。
作者:最初研究目标确实是可解释性
热烈讨论的结果就是,作者之一 Sachin Vaidya 站出来了。
作为该论文的作者之一,我想说几句。KAN 受到的关注令人惊叹,而这种讨论正是将新技术推向极限、找出哪些可行或不可行所需要的。
我想我应该分享一些关于动机的背景资料。我们实现 KAN 的主要想法源于我们正在寻找可解释的人工智能模型,这种模型可以「学习」物理学家发现自然规律的洞察力。因此,正如其他人所意识到的那样,我们完全专注于这一目标,因为传统的黑箱模型无法提供对科学基础发现至关重要的见解。然后,我们通过与物理学和数学相关的例子表明,KAN 在可解释性方面大大优于传统方法。我们当然希望,KAN 的实用性将远远超出我们最初的动机。
在 GitHub 主页中,论文作者之一刘子鸣也对这项研究受到的评价进行了回应:
最近我被问到的最常见的问题是 KAN 是否会成为下一代 LLM。我对此没有很清楚的判断。
KAN 专为关心高精度和可解释性的应用程序而设计。我们确实关心 LLM 的可解释性,但可解释性对于 LLM 和科学来说可能意味着截然不同的事情。我们关心 LLM 的高精度吗?缩放定律似乎意味着如此,但可能精度不太高。此外,对于 LLM 和科学来说,准确性也可能意味着不同的事情。
我欢迎人们批评 KAN,实践是检验真理的唯一标准。很多事情我们事先并不知道,直到它们经过真正的尝试并被证明是成功还是失败。尽管我愿意看到 KAN 的成功,但我同样对 KAN 的失败感到好奇。
KAN 和 MLP 不能相互替代,它们在某些情况下各有优势,在某些情况下各有局限性。我会对包含两者的理论框架感兴趣,甚至可以提出新的替代方案(物理学家喜欢统一理论,抱歉)。

KAN 论文一作刘子鸣。他是一名物理学家和机器学习研究员,目前是麻省理工学院和 IAIFI 的三年级博士生,导师是 Max Tegmark。他的研究兴趣主要集中在人工智能 AI 和物理的交叉领域。