昨天在群里面看到耳濡目染同志发了这么一张图。
 图片
图片
问的是 -1155459666 怎么变成 3139507630,这个问题比较有意思,虽然简单,但涉及到了原码、反码、补码相关的知识,本篇文章就来详细解释一下。
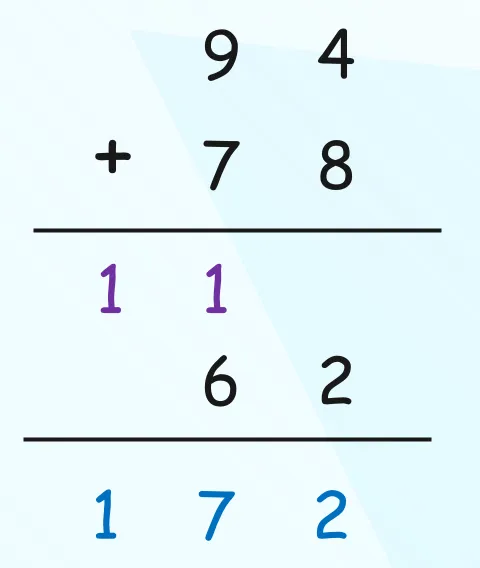
抛出一个问题,有两个整数 94、78,如果让你计算它们的和,你会怎么做?不用想,我们都会像下面这样。
 图片
图片
十进制是逢十进一,当产生溢出时会往前进一位,因此结果就是 110 + 062 等于 172。但计算机在运算时会使用二进制,本质是一样的,只不过二进制是逢二进一。
 图片
图片
我们验证一下。
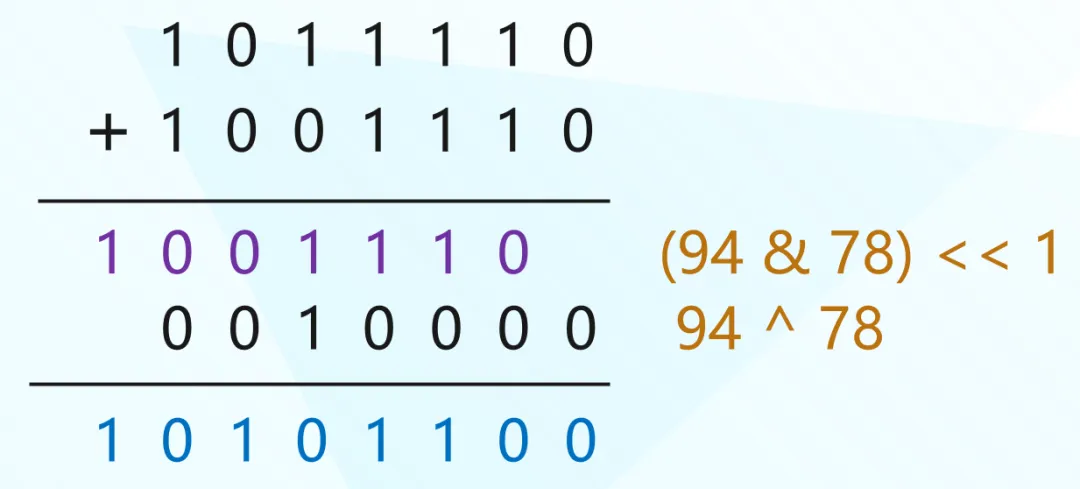
另外我们知道,与运算时,如果两个二进制位均是 1,那么结果是 1,否则结果是 0;异或运算时,如果两个二进制位相同,结果是 0,否则结果是 1。
然后再观察一下之前的式子。
 图片
图片
所以当两个整数相加时,我们还可以这么做。
当然两个整数直接相加的话,这么做没啥意义,它一般会应用于二分查找。在二分查找中,为了避免两个整数相加溢出,求平均值的时候一般会这么做。
然后来说一说原码、反码和补码,不过首先我们要知道负数是如何表示的,对于一个有符号整数来说,它的最高位表示符号位。比如一个 8 位整数:
 图片
图片
开头的符号位如果为 0,则表示正数,为 1 则表示负数,然后剩余的有效位则表示具体的数值。比如 15 的二进制是 1111,那么:
- 八位整数 15 的二进制就是 00001111;
- 八位整数 -15 的二进制就是 10001111;
由于 7 个位能表示的最大整数是 2 的 7 次方减 1,所以八位整数的最大值就是 127,而最小值是 -128。那么问题来了,为什么最小值是 -128 呢?这就涉及到原码、反码和补码了。
计算机为了人类阅读方便,会以原码的形式展示,但在计算和存储的时候则是以补码的形式。
- 对于正数来说,它的原码、反码、补码是相同的。
- 对于负数来说,它的反码等于原码的符号位不变、其它位取反(1 变 0,0 变 1),而补码则等于反码加 1。当然这是基于原码求补码,反过来也是一样。反码也等于补码的符号位不变、其它位取反,然后再加 1 得到原码,过程是一样的。
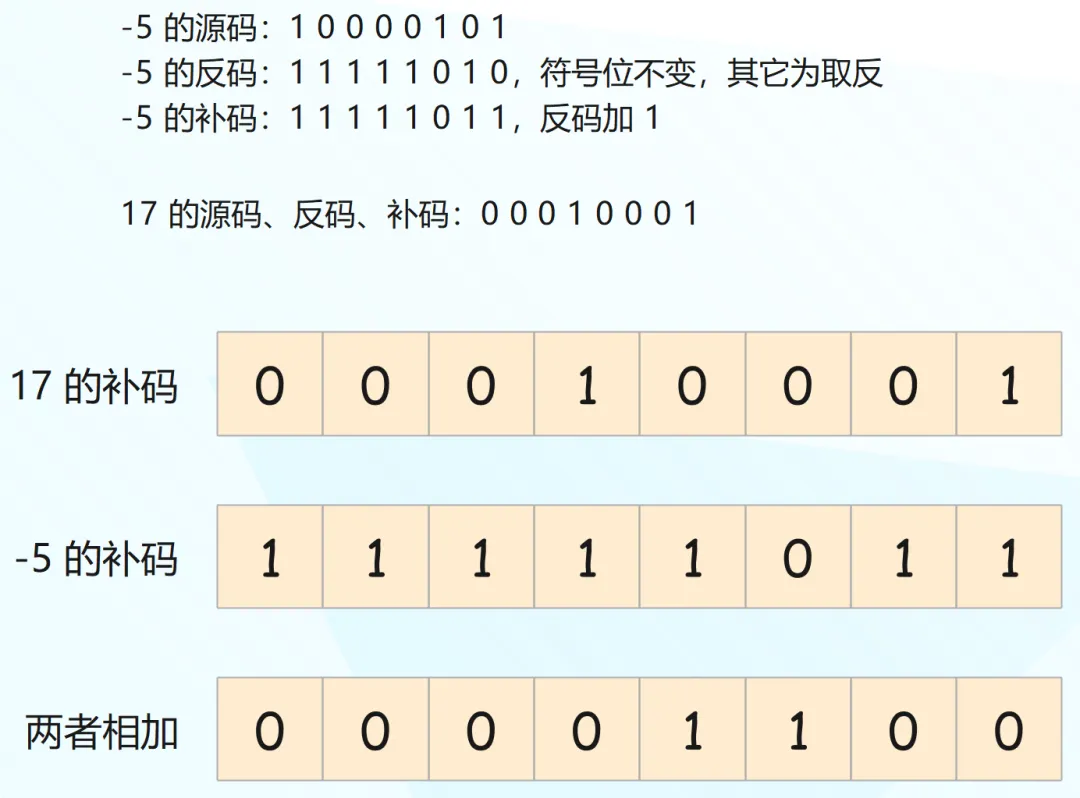
我们举个例子,假设两个八位整数 17 和 -5 相加。
 图片
图片
因此 00001100 就是两个整数的补码相加之后的结果,也就是 12,由于是正数,它的原码和反码也是 12。
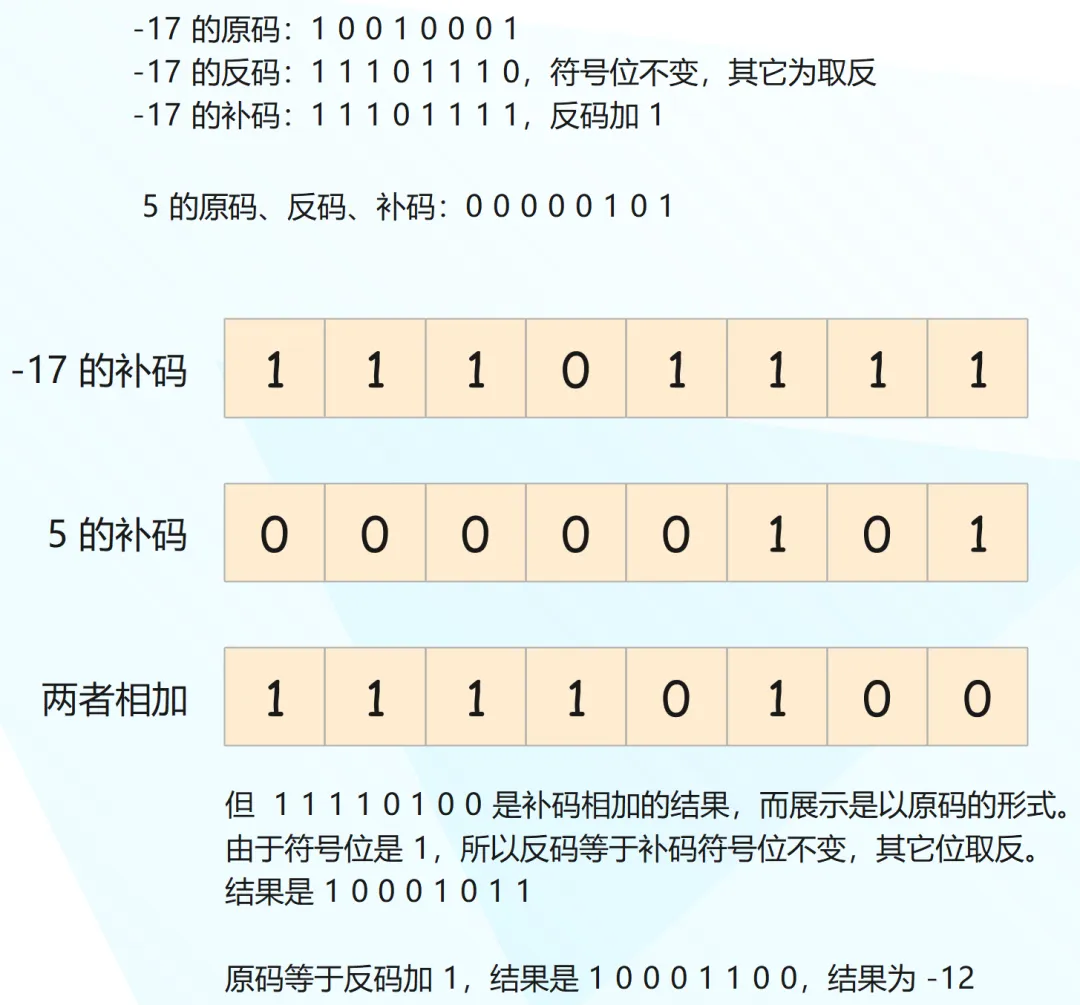
再举个例子,假设两个八位整数 -17 和 5 相加。
 图片
图片
相信你应该明白整个逻辑了,计算机在存储整数时会以补码存储,运算也是以补码的形式,但展示则是以原码的形式。我们以 C 语言为例,来直观感受一下这个过程。
我们再举个例子:
总结,对于一个有符号整数来说:
- 如果是正数(符号位是 0),它的原码、反码、补码是一致的。
- 如果是负数(符号位是 1),反码等于原码的符号位不变、其它位取反,补码等于反码加 1;或者反码等于补码的符号位不变、其它位取反,原码等于反码加 1。
计算机存储和运算使用的都是补码,但展示的是原码。
现在回到开头的问题了,-1155459666 是怎么变成 3139507630 的。
 图片
图片
还是那句话,不看你怎么存,就看你怎么读,反正存储的就是这一坨二进制。如果以有符号格式读取,最高位是符号位,结果就是 -1155459666;以无符号格式读取,最高位也是有效位,结果就是 3139507630。
那么问题来了,为什么要整出补码这个东西出来呢?很好理解,有了补码,加法和减法可以共用一套逻辑,无论是 a + b 还是 a - b,底层的运算逻辑是相同的。
最后再来解释一下,为什么有符号八位整数的最大值是 127,最小值是 -128。
 图片
图片
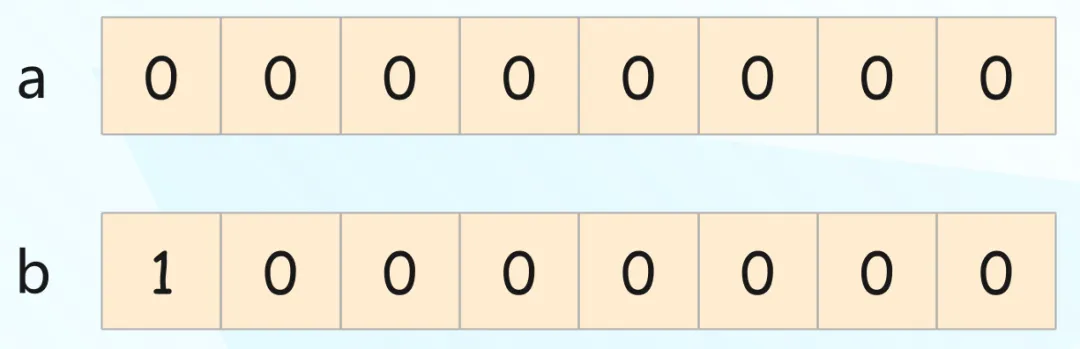
两个整数 a 和 b,首先 a 的值肯定是 0,但问题是 b 的值是多少?难道是 -0 吗?如果不考虑 0,那么有符号八位整数能表达的正数范围是 1 ~ 127,负数范围是 -1 ~ -127,然后还剩下两个 0。于是让 00000000 表示 0,让 10000000 表示 -128。
 图片
图片
不管是多少位的有符号整数,它的最小值的绝对值一定比最大值多 1,因此八位整数的最小值是 -128,最大值是 127。
事实上 10000000 表示 -128 有些人为规定的意思,但它确保了数字范围的对称性,并允许有效地利用二进制位来表达整数。
以上就是整数在底层的存储方式,以及原码、反码、补码之间的关系。































