本文经自动驾驶之心公众号授权转载,转载请联系出处。
0.简介
本文介绍了BEVTrack:鸟瞰图中点云跟踪的简单基线。由于点云的外观变化、外部干扰和高度稀疏性,点云的3D单目标跟踪(SOT)仍然是一个具有挑战性的问题。值得注意的是,在自动驾驶场景中,目标物体通常在连续帧间保持空间邻接,多数情况下是水平运动。这种空间连续性为目标定位提供了有价值的先验知识。然而,现有的跟踪器通常使用逐点表示,难以有效利用这些知识,这是因为这种表示的格式不规则。因此,它们需要精心设计并且解决多个子任务以建立空间对应关系。本文《BEVTrack: A Simple Baseline for 3D Single Object Tracking in Bird’s-Eye View》(https://arxiv.org/pdf/2309.02185.pdf)中的BEVTrack是一种简单而强大的三维单目标跟踪基线框架。在将连续点云转换为常见的鸟瞰图表示后,BEVTrack固有地对空间近似进行编码,并且通过简单的逐元素操作和卷积层来熟练捕获运动线索进行跟踪。此外,为了更好地处理具有不同大小和运动模式的目标,BEVTrack直接学习潜在的运动分布,而不像先前的工作那样做出固定的拉普拉斯或者高斯假设。BEVTrack在KITTI和NuScenes数据集上实现了最先进的性能,同时维持了122FPS的高推理速度。目前这个项目已经在Github(https://github.com/xmm-prio/BEVTrack)上开源了。
1.主要贡献
本文的贡献总结如下:
1)本文提出了BEVTrack,这是一种简单而强大的三维单目标跟踪的基线框架。这种开创性的方法通过BEV表示有效地利用了空间信息,从而简化了跟踪流程设计;
2)本文提出了一种新型的分布感知回归策略,其直接学习具有不同大小和各种运动模式的目标的潜在运动分布。该策略为跟踪提供准确的指导,从而提供了性能,同时避免了额外的计算开销;
3)BEVTrack在保持高推理速度的同时,在两个主流的基准上实现了最先进的性能
2.概述

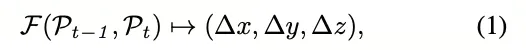
其中F是跟踪器学习到的映射函数。
根据公式(1),我们提出了BEVTrack,这是一个简单但强大的3D单目标跟踪基准框架。BEVTrack的整体架构如图2所示。它首先利用共享的VoxelNext [29]提取3D特征,然后将其压缩以获得BEV表示。随后,BEVTrack通过串联和多个卷积层融合BEV特征,并通过MLP回归目标的平移。为了实现准确的回归,我们采用了一种新颖的分布感知回归策略来优化BEVTrack的训练过程。
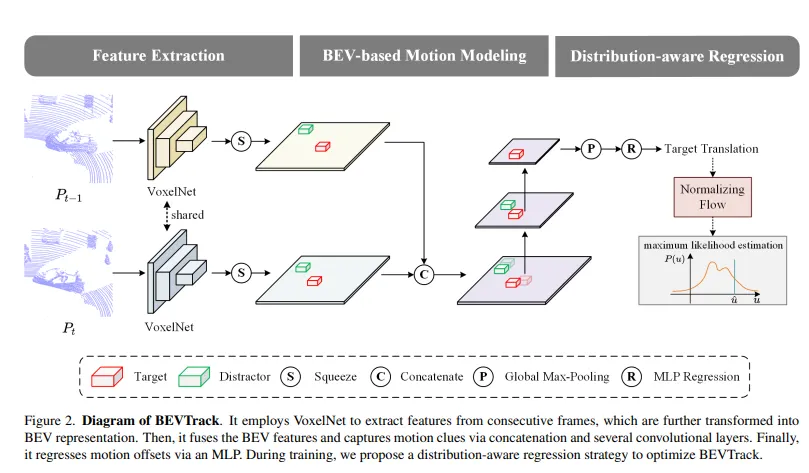
图2. BEVTrack的示意图。它使用VoxelNet从连续帧中提取特征,进一步将其转换为BEV表示。然后,通过串联和几个卷积层,它融合BEV特征并捕捉运动线索。最后,通过多层感知机(MLP)回归运动偏移量。在训练过程中,我们提出了一种分布感知回归策略来优化BEVTrack。
3.特征提取

4.基于BEV的运动建模

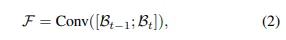
其中Conv表示BMM中的卷积块,[;][;]表示连接运算符。
其中H^′、W^′和C^′分别表示空间维度和特征通道数。
最后,我们使用最大池化层和多层感知器(MLP)来预测目标平移偏移,即,
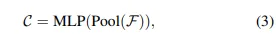
其中C ∈ \mathbb{R}^6表示目标平移偏移\bar{u} ∈ \mathbb{R}^3的期望值和标准差σ ∈ \mathbb{R}^3,这将在第5节中详细介绍。通过将平移应用于目标的最后状态,我们可以在当前帧中定位目标。
5.分布感知回归
在先前的工作中,通常在训练过程中使用传统的L1或L2损失来进行目标位置回归,这实际上对目标位置的分布做出了固定的拉普拉斯或高斯假设。与之相反,我们提出直接学习底层运动分布,并引入一种新颖的分布感知回归策略。通过这种方式,可以为跟踪提供更准确的指导,使BEVTrack能够更好地处理具有不同大小和移动模式的物体。
在[11]的基础上,我们使用重新参数化来建模目标平移偏移u∼P(u)的分布。具体而言,P(u)可以通过对来自零均值分布z∼P_Z(z)进行缩放和平移得到,其中u=\bar{u}+σ·z,其中\bar{u}表示目标平移偏移的期望,σ表示分布的尺度。P_Z(z)可以通过归一化流模型(例如,real NVP [2])进行建模。给定这个变换函数,可以计算出P(u)的密度函数:
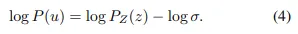
与之前仅回归确定性目标翻译偏移量u的方法相比,我们的方法专注于回归两个不同的参数:目标翻译偏移量u的期望值\bar{u}和其标准差σ。
在这项工作中,我们采用了[11]中的残差对数似然估计(RLE)来估计上述参数。RLE将分布P_Z(z)分解为一个先验分布Q_Z(z)(例如,拉普拉斯分布或高斯分布)和一个学习到的分布G_Z(z | θ)。为了最大化方程(4)中的似然函数,我们可以最小化以下损失函数: