以神经网络为基础的深度学习技术已经在诸多应用领域取得了有效成果。在实践中，网络架构可以显著影响学习效率，一个好的神经网络架构能够融入问题的先验知识，稳定网络训练，提高计算效率。目前，经典的网络架构设计方法包括人工设计、神经网络架构搜索（NAS）[1]、以及基于优化的网络设计方法 [2]。人工设计的网络架构如 ResNet 等；神经网络架构搜索则通过搜索或强化学习的方式在搜索空间中寻找最佳网络结构；基于优化的设计方法中的一种主流范式是算法展开（algorithm unrolling），该方法通常在有显式目标函数的情况下，从优化算法的角度设计网络结构。
然而，现有经典神经网络架构设计大多忽略了网络的万有逼近性质 —— 这是神经网络具备强大性能的关键因素之一。因此，这些设计方法在一定程度上失去了网络的先验性能保障。尽管两层神经网络在宽度趋于无穷的时候就已具有万有逼近性质 [3]，在实际中，我们通常只能考虑有限宽的网络结构，而这方面的表示分析的结果十分有限。实际上，无论是启发性的人工设计，还是黑箱性质的神经网络架构搜索，都很难在网络设计中考虑万有逼近性质。基于优化的神经网络设计虽然相对更具解释性，但其通常需要一个显式的目标函数，这使得设计的网络结构种类有限，限制了其应用范围。如何系统性地设计具有万有逼近性质的神经网络架构，仍是一个重要的问题。
为了解决这个问题，北京大学林宙辰教授团队提出了一种易于操作的基于优化算法设计具有万有逼近性质保障的神经网络架构的方法，其通过将基于梯度的一阶优化算法的梯度项映射为具有一定性质的神经网络模块，再根据实际应用问题对模块结构进行调整，就可以系统性地设计具有万有逼近性质的神经网络架构，并且可以与现有大多数基于模块的网络设计的方法无缝结合。论文还通过分析神经网络微分方程（NODE）的逼近性质首次证明了具有一般跨层连接的神经网络的万有逼近性质，并利用提出的框架设计了 ConvNext、ViT 的变种网络，取得了超越 baseline 的结果。论文被人工智能顶刊 TPAMI 接收。
- 论文：Designing Universally-Approximating Deep Neural Networks: A First-Order Optimization Approach
- 论文地址：https://ieeexplore.ieee.org/document/10477580
方法简介
传统的基于优化的神经网络设计方法通常从一个具有显式表示的目标函数出发，采用特定的优化算法进行求解，再将优化迭代格式映射为神经网络架构，例如著名的 LISTA-NN 就是利用 LISTA 算法求解 LASSO 问题所得 [4]，这种方法受限于目标函数的显式表达式，可设计得到的网络结构有限。一些研究者尝试通过自定义目标函数，再利用算法展开等方法设计网络结构，但他们也需要如权重绑定等与实际情况可能不符的假设。
论文提出的易于操作的网络架构设计方法从一阶优化算法的更新格式出发，将梯度或邻近点算法写成如下的更新格式：
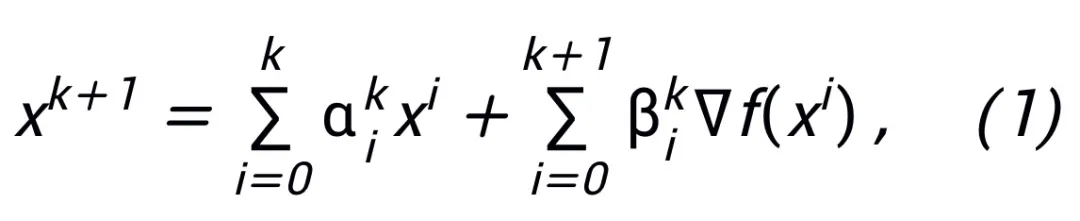
其中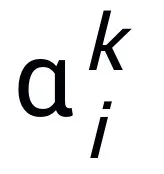
、
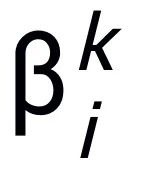表示第 k 步更新时的（步长）系数，再将梯度项替换为神经网络中的可学习模块 T，即可得到 L 层神经网络的骨架：
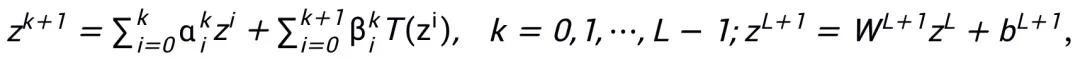
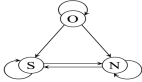
整体方法框架见图 1。
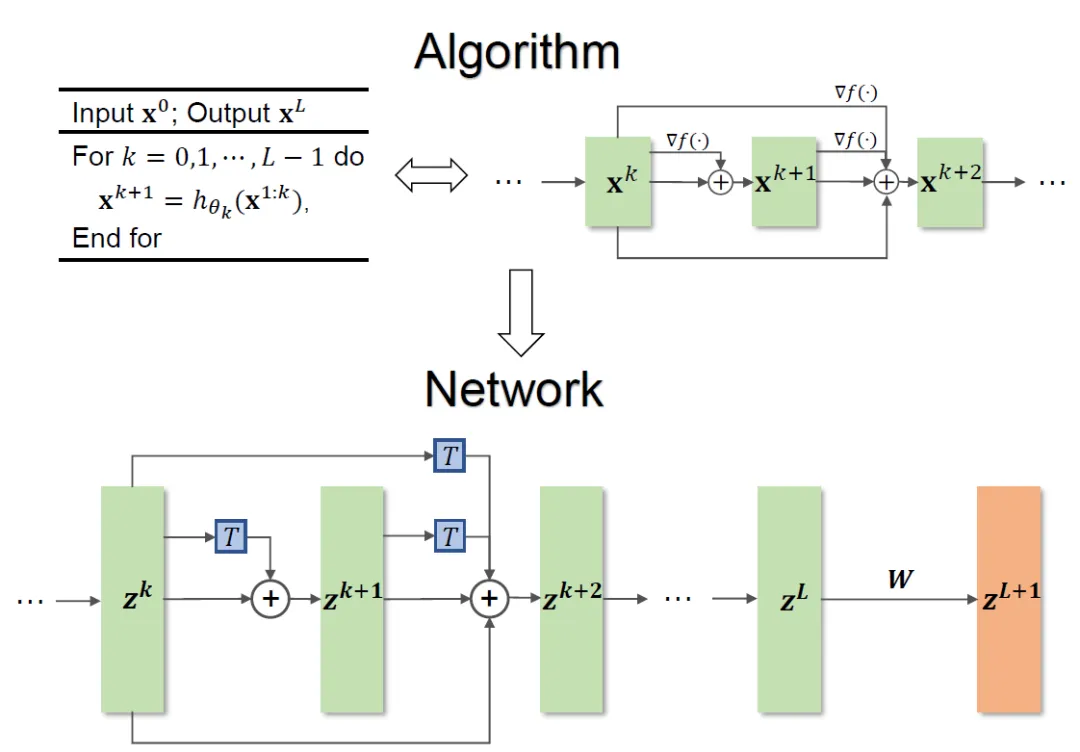
图 1 网络设计图示
论文提出的方法可以启发设计 ResNet、DenseNet 等经典网络，并且解决了传统基于优化设计网络架构的方法局限于特定目标函数的问题。
模块选取与架构细节
该方法所设计的网络模块 T 只要求有包含两层网络结构，即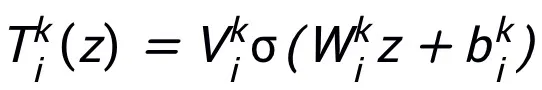
，作为其子结构，即可保证所设计的网络具有万有逼近性质，其中所表达的层的宽度是有限的（即不随逼近精度的提高而增长），整个网络的万有逼近性质不是靠加宽
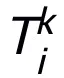的层来获得的。模块 T 可以是 ResNet 中广泛运用的 pre-activation 块，也可以是 Transformer 中的注意力 + 前馈层的结构。T 中的激活函数可以是 ReLU、GeLU、Sigmoid 等常用激活函数。还可以根据具体任务在中添加对应的归一化层。另外，
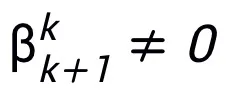时，设计的网络是隐式网络 [5]，可以用不动点迭代的方法逼近隐格式，或采用隐式微分（implicit differentiation）的方法求解梯度进行更新。
通过等价表示设计更多网络
该方法不要求同一种算法只能对应一种结构，相反，该方法可以利用优化问题的等价表示设计更多的网络架构，体现其灵活性。例如，线性化交替方向乘子法通常用于求解约束优化问题：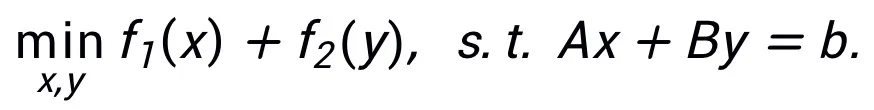
通过令
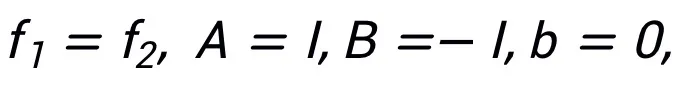即可得到一种可启发网络的更新迭代格式：
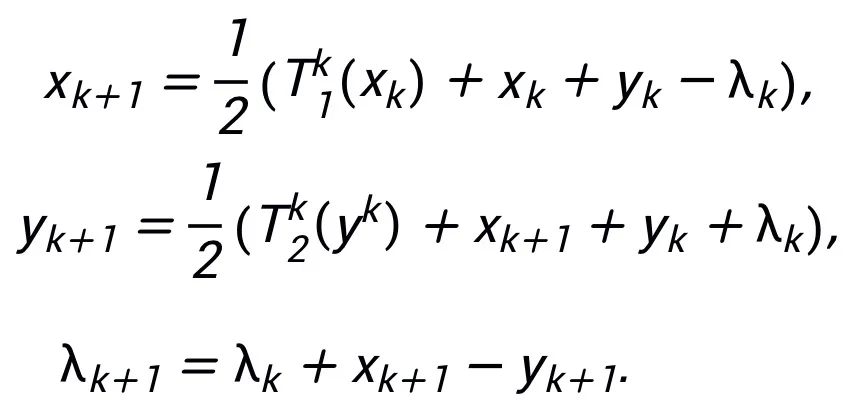
其启发的网络结构可见图 2。
图 2 线性化交替方向乘子法启发的网络结构
启发的网络具有万有逼近性质
对该方法设计的网络架构，可以证明，在模块满足此前条件以及优化算法（在一般情况下）稳定、收敛的条件下，任意一阶优化算法启发的神经网络在高维连续函数空间具有万有逼近性质，并给出了逼近速度。论文首次在有限宽度设定下证明了具有一般跨层连接的神经网络的万有逼近性质（此前研究基本集中在 FCNN 和 ResNet，见表 1），论文主定理可简略叙述如下：
主定理（简略版）：设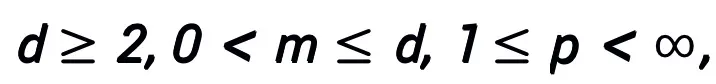
A 是一个梯度型一阶优化算法。若算法 A 具有公式 (1) 中的更新格式，且满足收敛性条件（优化算法的常用步长选取均满足收敛性条件。若在启发网络中均为可学习的，则可以不需要该条件），则由算法启发的神经网络：
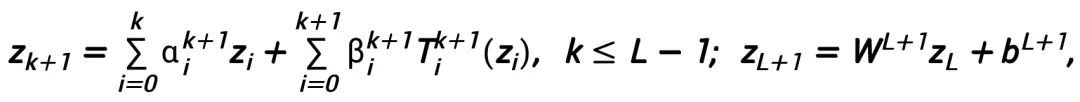
在连续（向量值）函数空间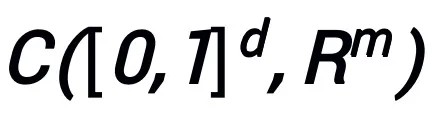
以及范数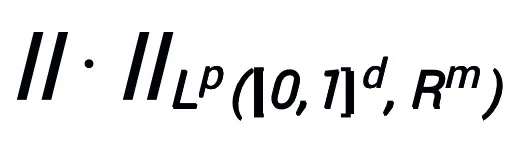
下具有万有逼近性质，其中可学习模块 T 只要有包含两层形如
的结构（σ 可以是常用的激活函数）作为其子结构都可以。
常用的 T 的结构如：
1）卷积网络中，pre-activation 块：BN-ReLU-Conv-BN-ReLU-Conv (z),
2）Transformer 中：Attn (z) + MLP (z+Attn (z)).
主定理的证明利用了 NODE 的万有逼近性质以及线性多步方法的收敛性质，核心是证明优化算法启发设计的网络结构恰对应一种收敛的线性多步方法对连续的 NODE 的离散化，从而启发的网络 “继承” 了 NODE 的逼近能力。在证明中，论文还给出了 NODE 逼近 d 维空间连续函数的逼近速度，解决了此前论文 [6] 的一个遗留问题。
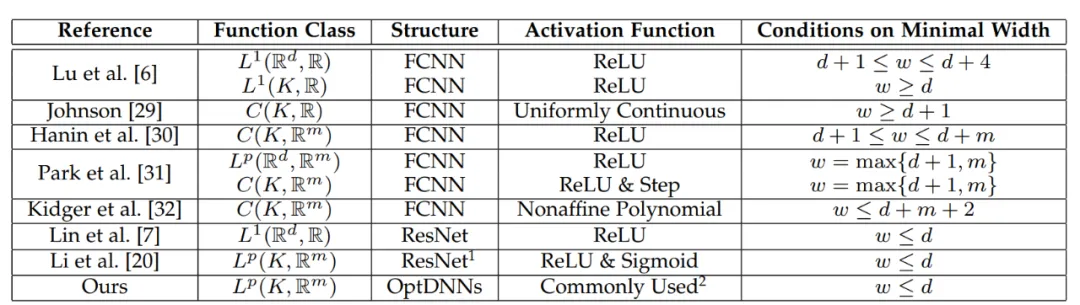
表 1 此前万有逼近性质的研究基本集中在 FCNN 和 ResNet
实验结果
论文利用所提出的网络架构设计框架设计了 8 种显式网络和 3 种隐式网络（称为 OptDNN），网络信息见表 2，并在嵌套环分离、函数逼近和图像分类等问题上进行了实验。论文还以 ResNet, DenseNet, ConvNext 以及 ViT 为 baseline，利用所提出的方法设计了改进的 OptDNN，并在图像分类的问题上进行实验，考虑准确率和 FLOPs 两个指标。
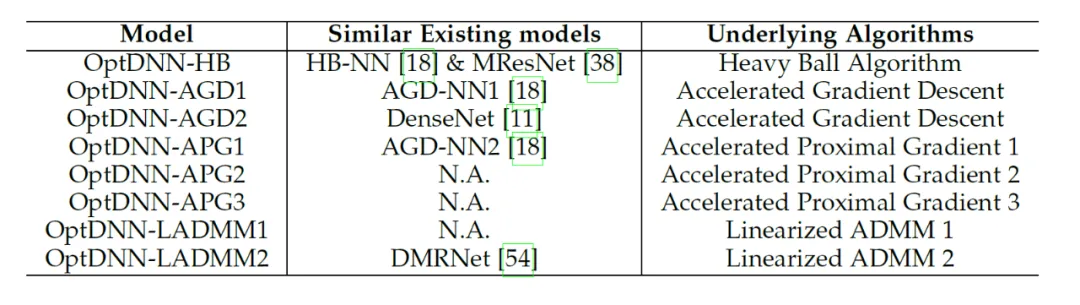
表 2 所设计网络的有关信息
首先，OptDNN 在嵌套环分离和函数逼近两个问题上进行实验，以验证其万有逼近性质。在函数逼近问题中，分别考虑了逼近 parity function 和 Talgarsky function，前者可表示为二分类问题，后者则是回归问题，这两个问题都是浅层网络难以逼近的问题。OptDNN 在嵌套环分离的实验结果如图 3 所示，在函数逼近的实验结果如图 3 所示，OptDNN 不仅取得了很好的分离 / 逼近结果，而且比作为 baseline 的 ResNet 取得了更大的分类间隔和更小的回归误差，足以验证 OptDNN 的万有逼近性质。
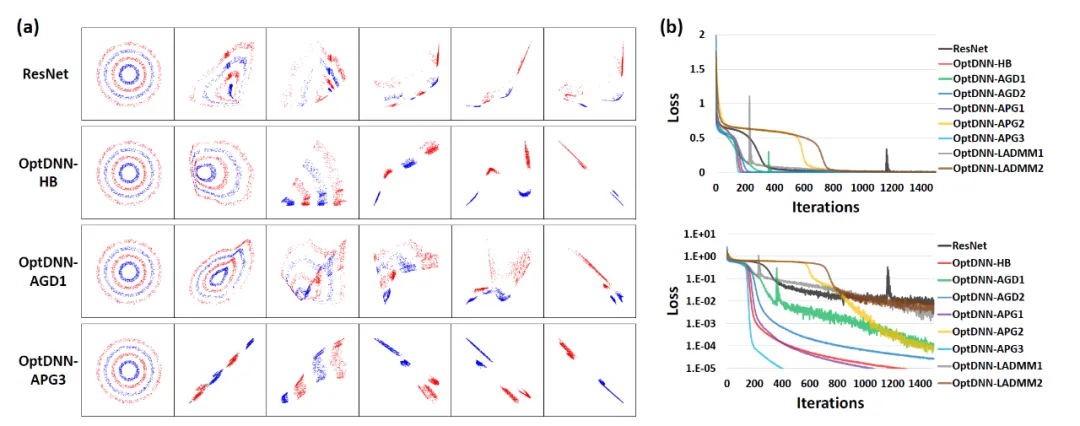
图 3 OptNN 逼近 parity function
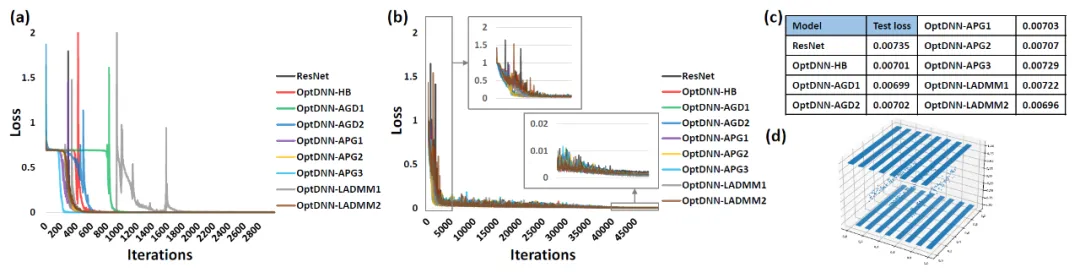
图 4 OptNN 逼近 Talgarsky function
然后，OptDNN 分别在宽 - 浅和窄 - 深两种设定下在 CIFAR 数据集上进行了图像分类任务的实验，结果见表 3 与 4。实验均在较强的数据增强设定下进行，可以看出，一些 OptDNN 在相同甚至更小的 FLOPs 开销下取得了比 ResNet 更小的错误率。论文还在 ResNet 和 DenseNet 设定下进行了实验，也取得了类似的实验结果。
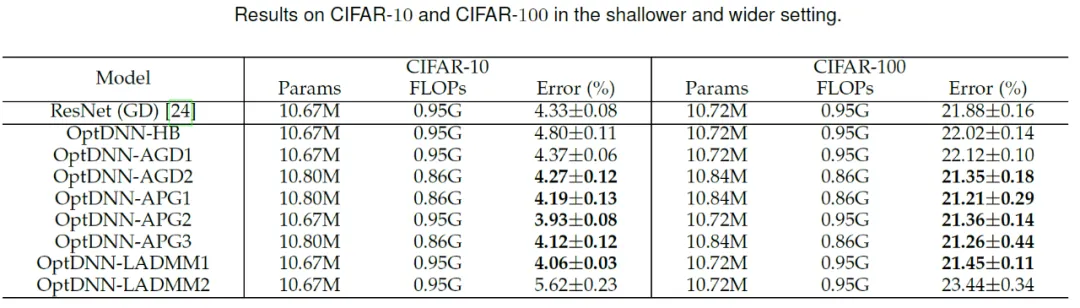
表 3 OptDNN 在宽 - 浅设定下的实验结果
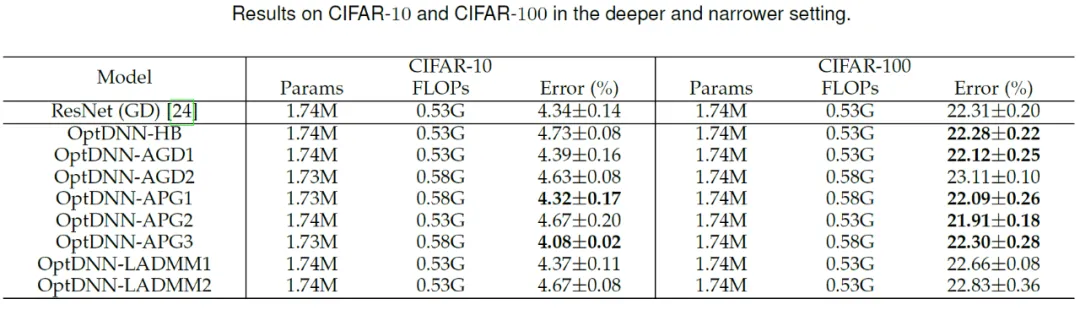
表 4 OptDNN 在窄 - 深设定下的实验结果
论文进一步选取了此前表现较好的 OptDNN-APG2 网络，进一步在 ConvNext 和 ViT 的设定下在 ImageNet 数据集上进行了实验，OptDNN-APG2 的网络结构见图 5，实验结果表 5、6。OptDNN-APG2 取得了超过等宽 ConvNext、ViT 的准确率，进一步验证了该架构设计方法的可靠性。
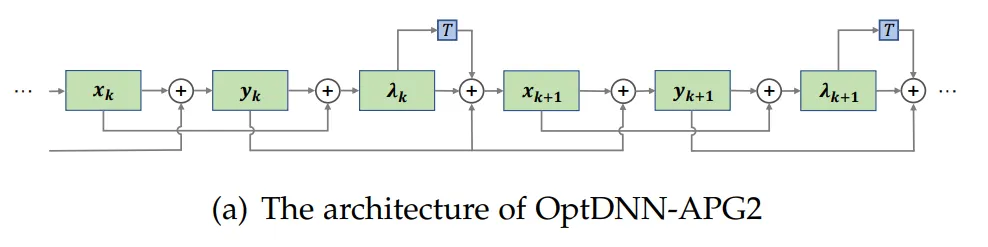
图 5 OptDNN-APG2 的网络结构
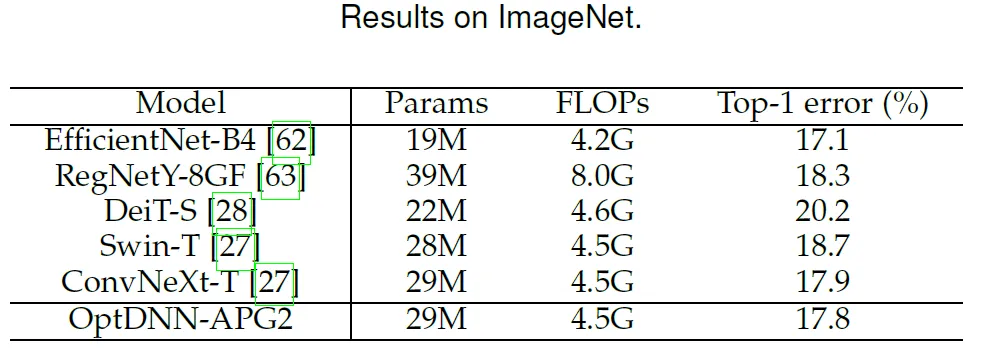
表 5 OptDNN-APG2 在 ImageNet 上的性能比较
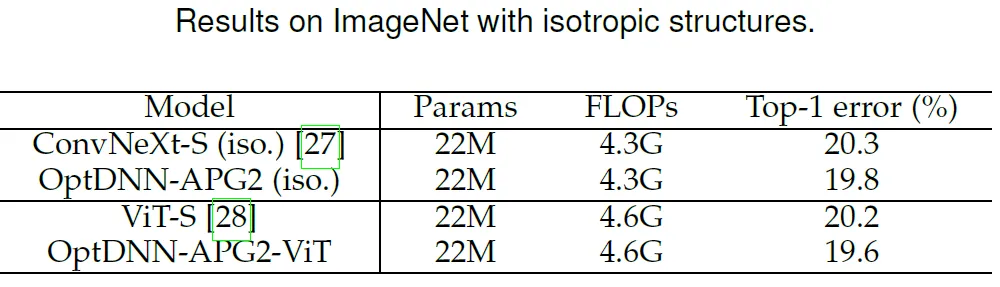
表 6 OptDNN-APG2 与等宽（isotropic）的 ConvNeXt 和 ViT 的性能比较
最后，论文依照 Proximal Gradient Descent 和 FISTA 等算法设计了 3 个隐式网络，并在 CIFAR 数据集上和显式的 ResNet 以及一些常用的隐式网络进行了比较，实验结果见表 7。三个隐式网络均取得了与先进隐式网络相当的实验结果，也说明了方法的灵活性。
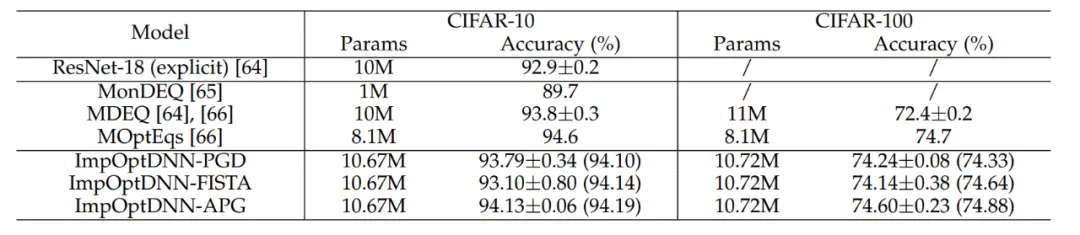
表 7 隐式网络的性能比较
总结
神经网络架构设计是深度学习中的核心问题之一。论文提出了一个利用一阶优化算法设计具有万有逼近性质保障的神经网络架构的统一框架，拓展了基于优化设计网络架构范式的方法。该方法可以与现有大部分聚焦网络模块的架构设计方法相结合，可以在几乎不增加计算量的情况下设计出高效的模型。在理论方面，论文证明了收敛的优化算法诱导的网路架构在温和条件下即具有万有逼近性质，并弥合了 NODE 和具有一般跨层连接网络的表示能力。该方法还有望与 NAS、 SNN 架构设计等领域结合，以设计更高效的网络架构。
