在这篇文章,我不仅会具体介绍之前没有讲到的回溯算法写法,还会告诉你为什么可以那样写,两种写法的本质区别是什么。
先说结论:
1、回溯算法穷举的本质思维模式是「球盒模型」,一切回溯算法,皆从此出,别无二法。
2、球盒模型,必然有两种穷举视角,分别为「球」的视角穷举和「盒」的视角穷举,对应的,就是两种不同的代码写法。
3、从理论上分析,两种穷举视角本质上是一样的。但是涉及到具体的代码实现,两种写法的复杂度可能有优劣之分。你需要选择效率更高的写法。
球盒模型这个词是我随口编的,因为下面我会用「球」和「盒」两种视角来解释,你理解就好。
暴力穷举思维方法:球盒模型
一切暴力穷举算法,都从球盒模型开始,没有例外。
你懂了这个,就可以随心所欲运用暴力穷举算法,下面的内容,请你仔细看,认真想。
首先,我们回顾一下以前学过的排列组合知识:
1、P(n, k)(也有很多书写成A(n, k))表示从n个不同元素中拿出k个元素的排列(Permutation/Arrangement)总数;C(n, k)表示从n个不同元素中拿出k个元素的组合(Combination)总数。
2、「排列」和「组合」的主要区别在于是否考虑顺序的差异。
3、排列、组合总数的计算公式:
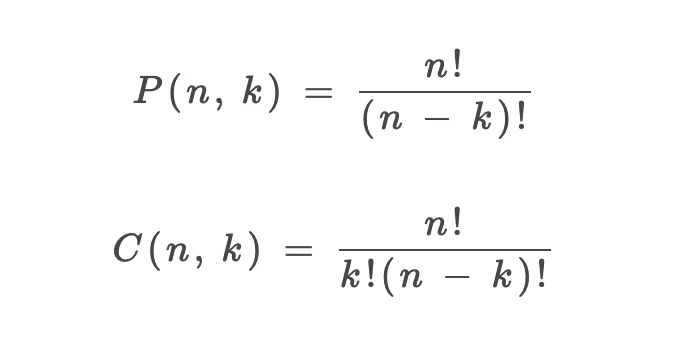 图片
图片
好,现在我问一个问题,这个排列公式P(n, k)是如何推导出来的?为了搞清楚这个问题,我需要讲一点组合数学的知识。
排列组合问题的各种变体都可以抽象成「球盒模型」,P(n, k)就可以抽象成下面这个场景:
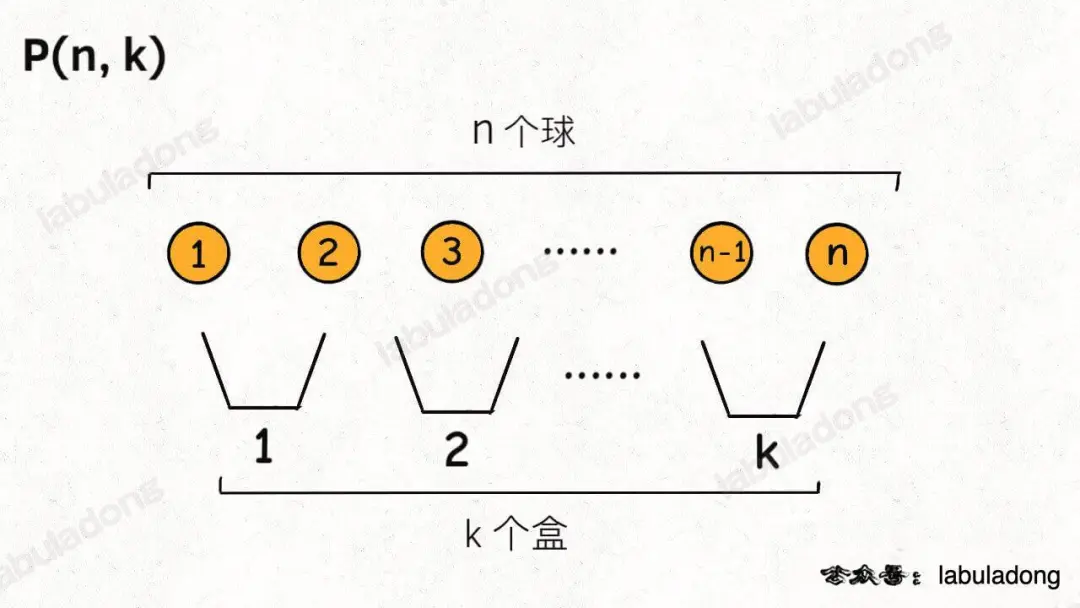 图片
图片
即,将n个标记了不同序号的球(标号为了体现顺序的差异),放入k个标记了不同序号的盒子中(其中n >= k,每个盒子最终都装有恰好一个球),共有P(n, k)种不同的方法。
现在你来,往盒子里放球,你怎么放?其实有两种视角。
首先,你可以站在盒子的视角,每个盒子必然要选择一个球。
这样,第一个盒子可以选择n个球中的任意一个,然后你需要让剩下k - 1个盒子在n - 1个球中选择:
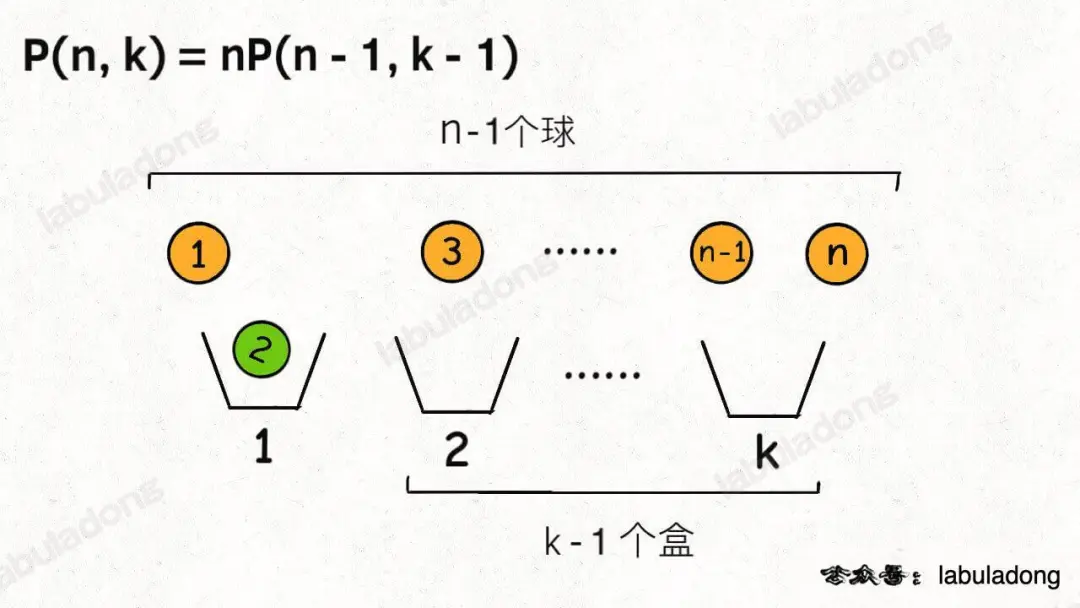 图片
图片
另外,你也可以站在球的视角,因为并不是每个球都会被装进盒子,所以球的视角分两种情况:
1、第一个球可以不装进任何一个盒子,这样的话你就需要将剩下n - 1个球放入k个盒子。
2、第一个球可以装进k个盒子中的任意一个,这样的话你就需要将剩下n - 1个球放入k - 1个盒子。
结合上述两种情况,可以得到:
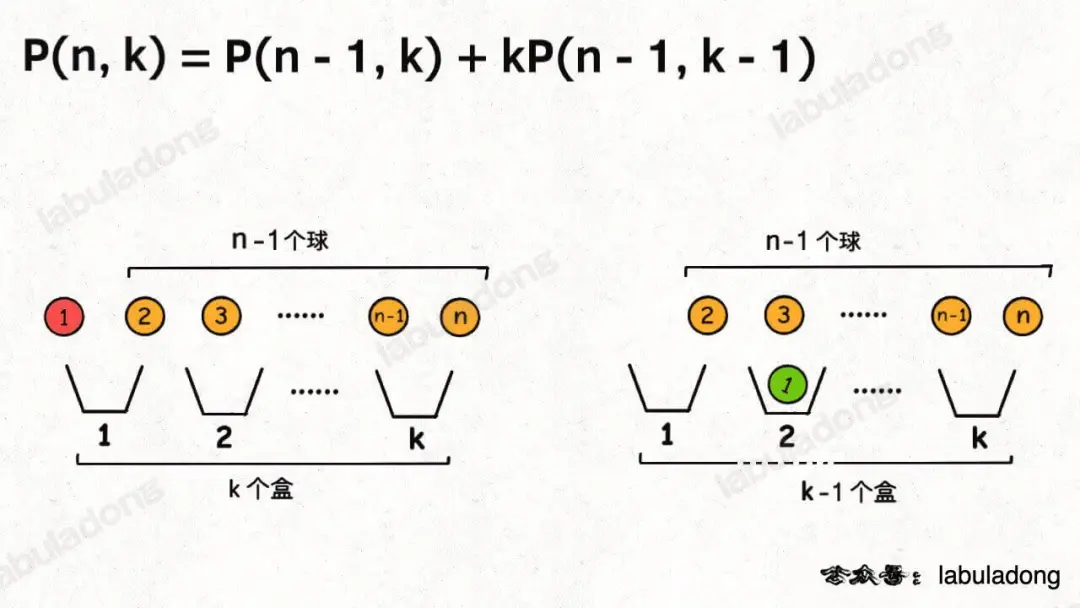 图片
图片
你看,两种视角得到两个不同的递归式,但这两个递归式解开的结果都是我们熟知的阶乘形式:
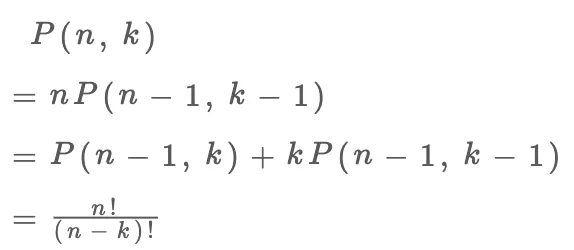 图片
图片
至于如何解递归式,涉及数学的内容比较多,这里就不做深入探讨了,有兴趣的读者可以自行学习组合数学相关知识。
用球盒模型重新理解全排列问题
好,上面从数学的角度介绍了全排列穷举的两种视角,现在回归到代码上,我要考你了哦。
前文 回溯算法核心框架 和 回溯算法秒杀排列/组合/子集的九种变体 都给出过全排列的代码。
就以最基本的元素无重不可复选的全排列为例,我直接把代码 copy 过来:
class Solution {
List<List<Integer>> res = new LinkedList<>();
// 记录回溯算法的递归路径
LinkedList<Integer> track = new LinkedList<>();
// track 中的元素会被标记为 true
boolean[] used;
/* 主函数,输入一组不重复的数字,返回它们的全排列 */
public List<List<Integer>> permute(int[] nums) {
used = new boolean[nums.length];
backtrack(nums);
return res;
}
// 回溯算法核心函数
void backtrack(int[] nums) {
// base case,到达叶子节点
if (track.size() == nums.length) {
// 收集叶子节点上的值
res.add(new LinkedList(track));
return;
}
// 回溯算法标准框架
for (int i = 0; i < nums.length; i++) {
// 已经存在 track 中的元素,不能重复选择
if (used[i]) {
continue;
}
// 做选择
used[i] = true;
track.addLast(nums[i]);
// 进入下一层回溯树
backtrack(nums);
// 取消选择
track.removeLast();
used[i] = false;
}
}
}请问,这个解法是以什么视角进行穷举的?是以球的视角还是盒的视角?给你三分钟思考,请回答!
这个代码是以盒的视角进行穷举的,即站在每个位置的角度来选择球,站在nums中的每个索引,来选择不同的元素放入这个索引位置。
为什么是这个答案呢?假设nums里面有n个数字,那么全排列问题相当于把n个球放到包含n个位置的盒子里,要求盒子必须装满,问你有几种不同的装法。
以盒的视角理解,盒子的第一个位置可以接收n个球的任意一个,有n种选择,第二个位置可以接收n - 1个球的任意一个,有n - 1种选择,第三个位置有n - 2种选择,以此类推。
我直接用 算法可视化面板 把递归树画出来,你一眼就可以看懂了。请你把进度条拖到最后让整棵回溯树显示出来,然后把鼠标在每一层节点上横向移动,观察递归树节点和树枝上的值:
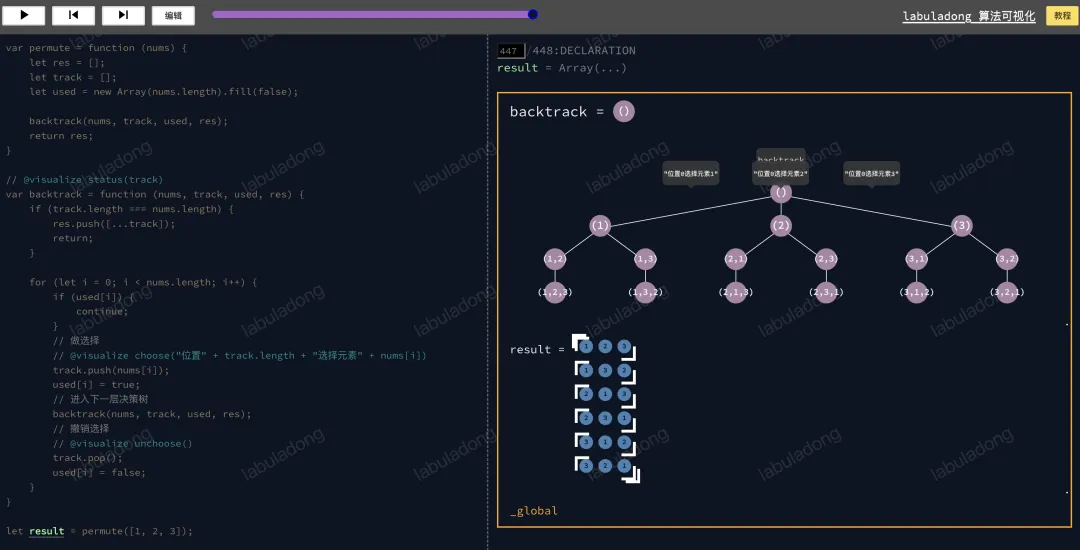 图片
图片
这个可视化面板的网页地址,你可以自己去试试:
https://labuladong.online/algo/practice-in-action/two-views-of-backtrack/#div_box-view-of-permute
其实这个算法还可以优化,也就是用 swap 的写法。
我在 回溯算法核心框架 和 回溯算法秒杀排列/组合/子集的九种变体 中都写了上面这段代码,很多读者看了之后就跑来跟我说啊,他看的那个全排列算法是通过swap操作来计算的,不需要used数组的额外空间,比我讲解的回溯算法框架效率高,怎么怎么的。
是的,我之所以不用那个swap的解法,是因为前面那两篇文章的重点在于实践回溯算法「做选择」和「撤销选择」的思维框架,用used数组的解法更容易让初学者理解。但从算法效率上说,确实有更高效的代码实现方法。
下面就满足大家的好奇心,跟大家讲讲那个传说中的swap的解法,到底是何方神圣。
首先,我列出那个使用swap计算全排列的解法代码,请你先看一下:
class Solution {
List<List<Integer>> result = new ArrayList<>();
public List<List<Integer>> permute(int[] nums) {
backtrack(nums, 0);
return result;
}
// 回溯算法核心框架
void backtrack(int[] nums, int start) {
if (start == nums.length) {
// 找到一个全排列,Java 需要转化成 List 类型
List<Integer> list = new ArrayList<>();
for (int num : nums) {
list.add(num);
}
result.add(list);
return;
}
for (int i = start; i < nums.length; i++) {
// 做选择
swap(nums, start, i);
// 递归调用,传入 start + 1
backtrack(result, nums, start + 1);
// 撤销选择
swap(nums, start, i);
}
}
void swap(int[] nums, int i, int j) {
int temp = nums[i];
nums[i] = nums[j];
nums[j] = temp;
}
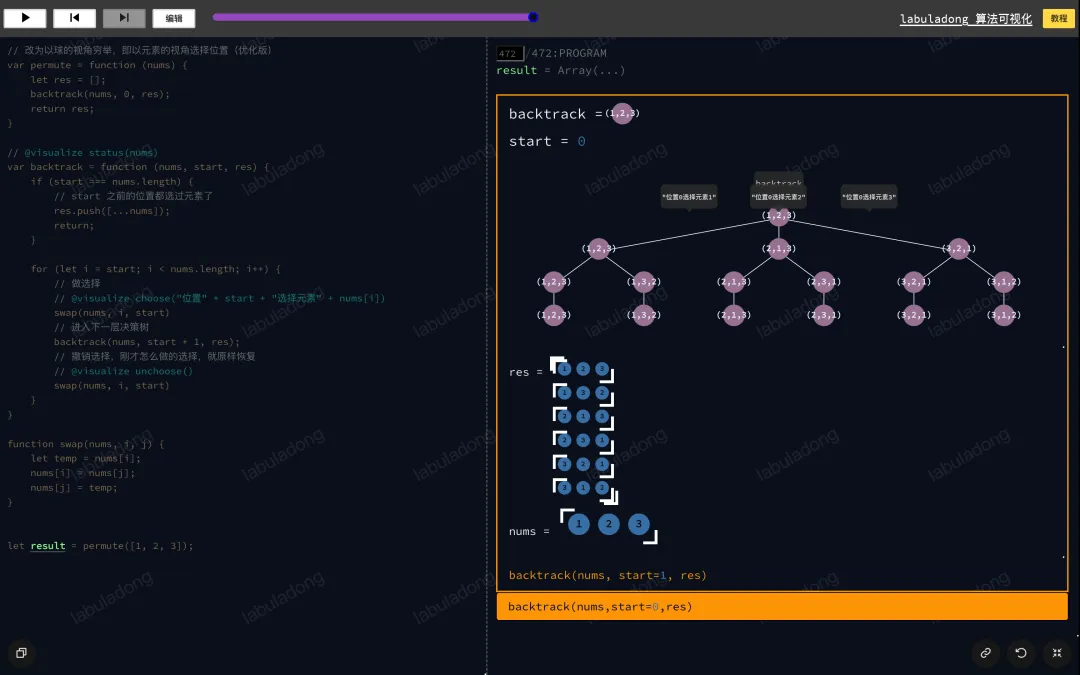
}这个解法也可以正确计算全排列,请你思考,这段代码是以什么视角进行穷举的?是以球的视角还是盒的视角?
答案是,这个解法是以盒的视角进行穷举的。即nums数组中的每个索引位置,来选择不同的元素放入这个索引位置。
你看解法代码也可以看出来,那个start参数就是当前在选择元素的索引位置,在start之前的元素已经心有所属,被其他位置挑走了,所以start位置只能从nums[start..]中选择元素。
我可以用 算法可视化面板 把递归树画出来,你一眼就可以看懂了。请你把进度条拖到最后让整棵回溯树显示出来,然后把鼠标在每一层节点上横向移动,观察递归树节点和树枝上的值:
 图片
图片
这个可视化面板的网页地址,你可以自己去试试:
https://labuladong.online/algo/practice-in-action/two-views-of-backtrack/#div_box-view-of-permute-improved
接下来一个很自然的问题,能不能写出一个以球的视角理解的全排列问题的解法?
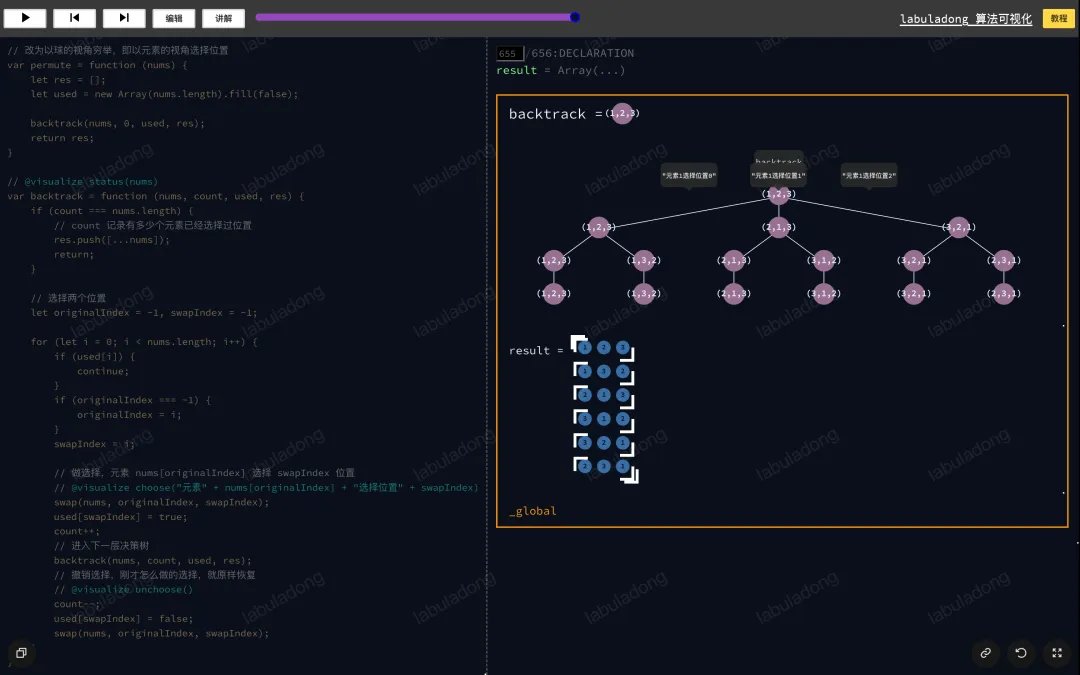
当然可以,以球的视角来写全排列的解法代码,就是说nums中的每个元素来选择自己想去的索引,对吧。有了这个思路,代码还有何难写。
我先用 算法可视化面板 把递归树画出来,请你把进度条拖到最后让整棵回溯树显示出来,然后把鼠标在每一层节点上横向移动,观察递归树节点和树枝上的值,验证一下是不是元素在选索引:
 图片
图片
这个可视化面板的网页地址,你可以自己去试试:
https://labuladong.online/algo/practice-in-action/two-views-of-backtrack/#div_ball-view-of-permute
当然我写的代码还有一些小优化的空间,比如说这个swapIndex其实就是i,而且我们其实不用等到count == nums.length,当count == nums.length - 1时就可以 return 了,因为最后剩的那个元素的位置不会找不到其他位置了。这些留给你优化吧。
class Solution {
List<List<Integer>> res; // 结果列表
boolean[] used; // 标记元素是否已被使用
int count; // 记录有多少个元素已经选择过位置
public List<List<Integer>> permute(int[] nums) {
res = new ArrayList<>();
used = new boolean[nums.length];
count = 0;
backtrack(nums);
return res;
}
// 回溯算法框架
void backtrack(int[] nums) {
if (count == nums.length) {
List<Integer> temp = new ArrayList<>();
for (int num : nums) {
temp.add(num);
}
res.add(temp);
return;
}
// 找两个未被选择的位置
int originalIndex = -1, swapIndex = -1;
for (int i = 0; i < nums.length; i++) {
if (used[i]) {
continue;
}
if (originalIndex == -1) {
originalIndex = i;
}
swapIndex = i;
// 做选择,元素 nums[originalIndex] 选择 swapIndex 位置
swap(nums, originalIndex, swapIndex);
used[swapIndex] = true;
count++;
// 进入下一层决策树
backtrack(nums);
// 撤销选择,刚才怎么做的选择,就原样恢复
count--;
used[swapIndex] = false;
swap(nums, originalIndex, swapIndex);
}
}
void swap(int[] nums, int i, int j) {
int temp = nums[i];
nums[i] = nums[j];
nums[j] = temp;
}
}用球盒模型重新理解子集问题
有了前面的铺垫,我又要进一步为难你了。回溯算法秒杀排列/组合/子集的九种变体 都给出过子集问题的代码。
就以最基本的元素无重不可复选的子集为例,我直接把代码 copy 过来:
class Solution {
List<List<Integer>> res = new LinkedList<>();
// 记录回溯算法的递归路径
LinkedList<Integer> track = new LinkedList<>();
// 主函数
public List<List<Integer>> subsets(int[] nums) {
backtrack(nums, 0);
return res;
}
// 回溯算法核心函数,遍历子集问题的回溯树
void backtrack(int[] nums, int start) {
// 前序位置,每个节点的值都是一个子集
res.add(new LinkedList<>(track));
// 回溯算法标准框架
for (int i = start; i < nums.length; i++) {
// 做选择
track.addLast(nums[i]);
// 通过 start 参数控制树枝的遍历,避免产生重复的子集
backtrack(nums, i + 1);
// 撤销选择
track.removeLast();
}
}
}请问,这个解法是以什么视角进行穷举的?是以球的视角还是盒的视角?给你三分钟思考,请回答!
这个解法是以盒的视角穷举的,即站在nums中的每个索引的视角,来选择不同的元素放入这个索引位置。
因为刚才讲的全排列问题会考虑顺序的差异,而子集问题不考虑顺序的差异。为了方便理解,我们这里干脆不说「球盒模型」了,说「球桶模型」吧,因为放进盒子的求给人感觉是有顺序的,而丢进桶里的东西给人感觉是无所谓顺序的。
那么,以桶的视角理解,子集问题相当于把n个球丢到容量为n的桶里,桶可以不装满。
这样,桶的第一个位置可以选择n个球中的任意一个,比如选择了球i,然后桶的第二个位置可以选择球i后面的球中的任意一个(通过固定相对顺序保证不会出现重复的子集),以此类推。
你看代码也能体现出来这种穷举过程:
// 回溯算法框架核心代码
void backtrack(int[] nums, int start) {
for (int i = start; i < nums.length; i++) {
track.addLast(nums[i]);
// 通过 start 参数控制树枝的生长
backtrack(nums, i + 1);
track.removeLast();
}
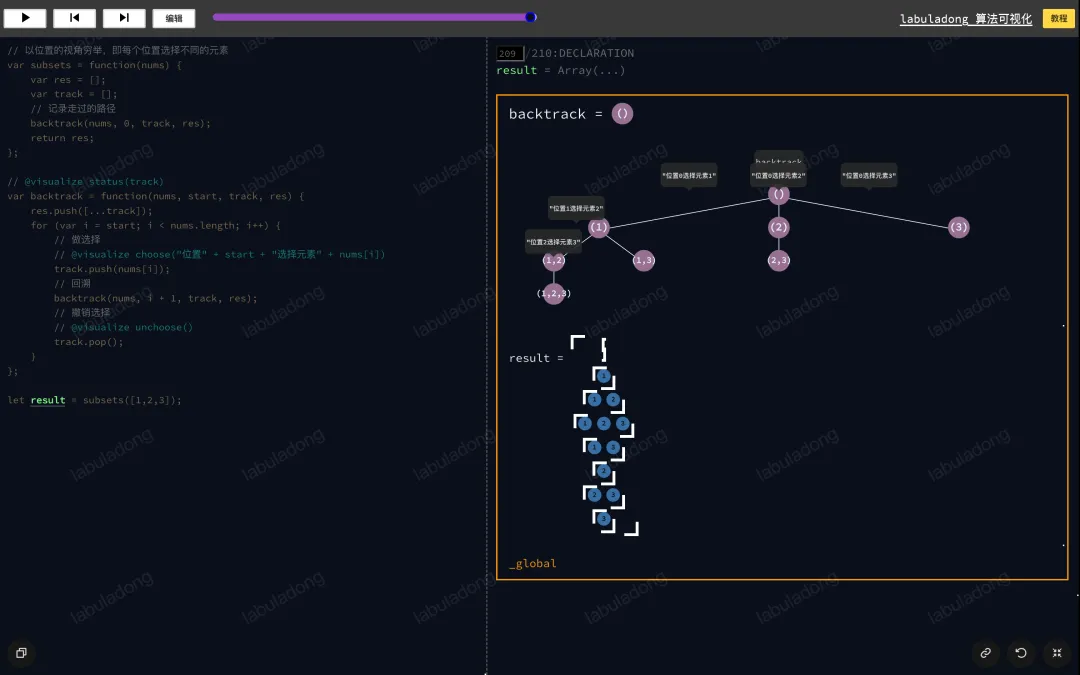
}我继续用 算法可视化面板 来论证我的答案,请你把进度条拖到最后让整棵回溯树显示出来,然后把鼠标在每一层节点上横向移动,观察递归树节点和树枝上的值,你可以很直观地看明白,是桶的位置在选择球:
 图片
图片
这个可视化面板的网页地址,你可以自己去试试:
https://labuladong.online/algo/practice-in-action/two-views-of-backtrack/#div_box-view-of-subsets
既然上面说了,我给的子集问题解法是以桶的视角理解的,那么你能不能写出一个以球的视角理解的子集问题的解法?给你十分钟写代码。
如果你有这个时间,一定要亲自动手尝试一下,不要着急看我的答案。你能认真看到这里,肯定可以写出来的。
从球的视角理解,每个球都有两种选择,要么在桶中,要么不在桶中。这样,我们可以写出下面的代码:
class Solution {
List<List<Integer>> res; // 用于存储所有子集的结果
List<Integer> track; // 用于存储当前递归路径的子集
public List<List<Integer>> subsets(int[] nums) {
res = new ArrayList<>();
track = new ArrayList<>();
backtrack(nums, 0);
return res;
}
void backtrack(int[] nums, int i) {
if (i == nums.length) {
res.add(new ArrayList<>(track));
return;
}
// 做第一种选择,元素在子集中
track.add(nums[i]);
backtrack(nums, i + 1);
// 撤销选择
track.remove(track.size() - 1);
// 做第二种选择,元素不在子集中
backtrack(nums, i + 1);
}
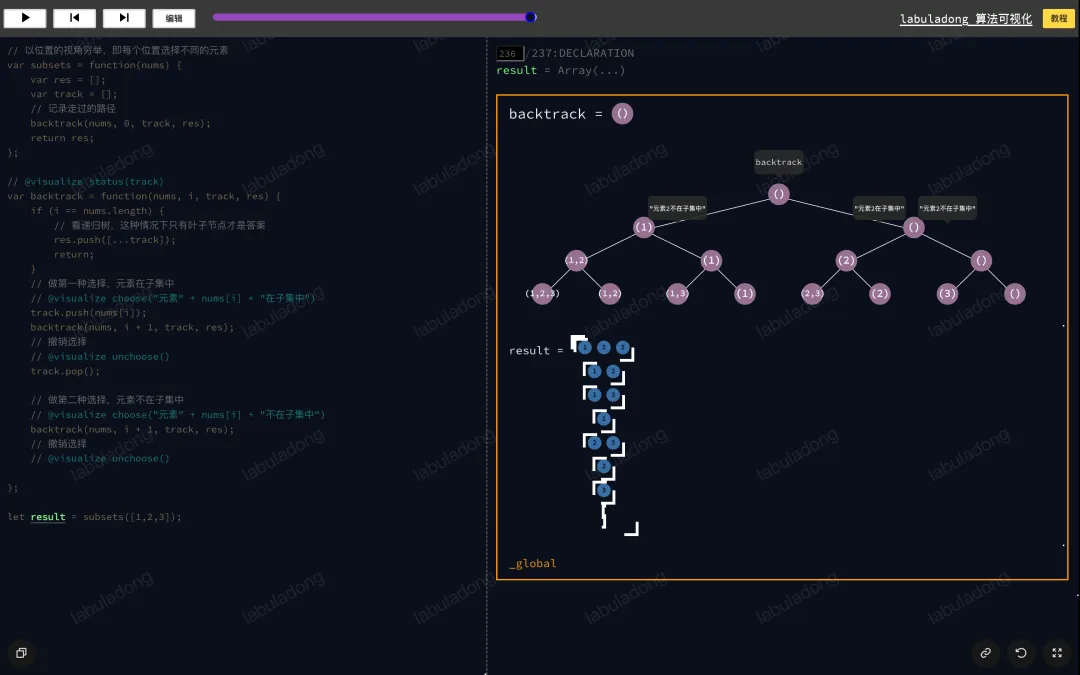
}我继续用 算法可视化面板 来论证我的答案,请你把进度条拖到最后让整棵回溯树显示出来,然后把鼠标在节点上移动,观察递归树节点和树枝上的值:
 图片
图片
这个可视化面板的网页地址,你可以自己去试试:
https://labuladong.online/algo/practice-in-action/two-views-of-backtrack/#div_ball-view-of-subsets
这也解释了,为什么所有子集(幂集)的数量是2^n,因为每个元素都有两种选择,要么在子集中,要么不在子集中,所以其递归树就是一棵满二叉树,一共有2^n个叶子节点。
结论
照应一下开头,把几个结论再重写一遍,你现在应该更理解了。
1、回溯算法穷举的本质思维模式是「球盒模型」,一切回溯算法,皆从此出,别无二法。
你现在就去做 100 道回溯算法的题目,看看有没有意外,有意外你来打我。
2、球盒模型,必然有两种穷举视角,分别为「球」的视角穷举和「盒」的视角穷举,对应的,就是两种不同的代码写法。
暴力穷举就是如此朴实无华且枯燥,看起来花里胡哨,实则只有两种视角。
3、从理论上分析,两种穷举视角本质上是一样的。但是涉及到具体的代码实现,两种写法的复杂度可能有优劣之分。
进一步想想,为啥用「盒」的视角,即让索引取选元素的视角,可以用swap的方法把used数组给优化掉呢?
因为索引容易处理,如果你按顺序从小到大让每个索引去选元素,那么一个start变量作为分割线就能把已选元素和未选元素分开。
反过来,如果你让元素去选索引,那就只能依赖额外的数据结构来记录那些索引已经被选过了,这样就会增加额外的空间复杂度。
所以说,在开头的数学分析中,两种视角在数学上虽然是等价的,但具体到代码实现上,最优复杂度就可能不一样。
好的,最后留个悬念:只有写回溯算法时才会用到「球盒模型」这种思想吗?
你可以读一读 动态规划算法的两种视角,思考一下这个问题。