机器学习的最优化算法是用于找到最佳模型参数,以最小化预测误差的算法。这些算法通过迭代地调整模型参数,以不断改进模型的性能。
本文系统地介绍了优化算法,基本脉络是从优化的基础知识,到各种优化算法原理的介绍及代码示例,最后放上各种算法的对比及实践经验总结!
一、基础知识
1.1 梯度(一阶导数)
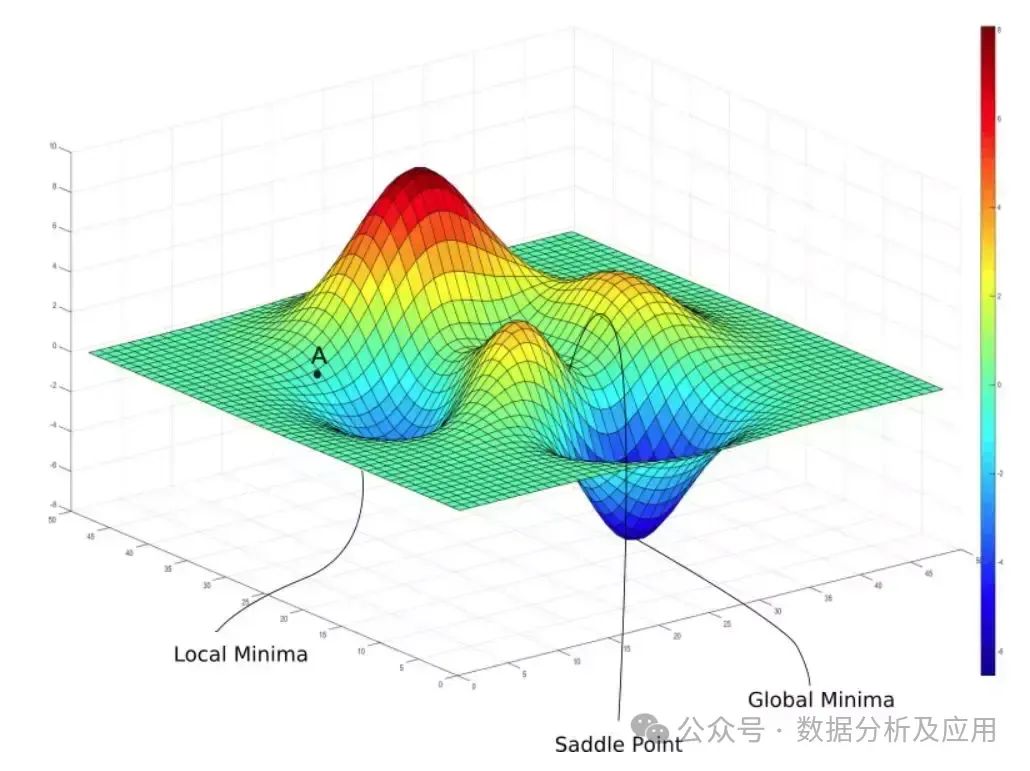
考虑一座在 (x1, x2) 点高度是 f(x1, x2) 的山。那么,某一点的梯度方向是在该点坡度最陡的方向,而梯度的大小告诉我们坡度到底有多陡。注意,梯度也可以告诉我们不在最快变化方向的其他方向的变化速度(二维情况下,按照梯度方向倾斜的圆在平面上投影成一个椭圆)。对于一个含有 n 个变量的标量函数,即函数输入一个 n 维 的向量,输出一个数值,梯度可以定义为:
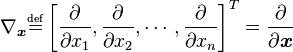
1.2 Hesse 矩阵(二阶导数)
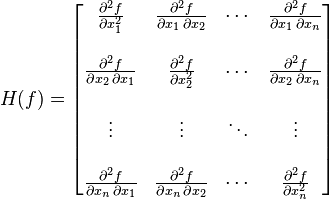
Hesse 矩阵常被应用于牛顿法解决的大规模优化问题(后面会介绍),主要形式如下:
当 f(x) 为二次函数时,梯度以及 Hesse 矩阵很容易求得。二次函数可以写成下列形式:
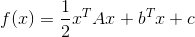
其中 A 是 n 阶对称矩阵,b 是 n 维列向量, c 是常数。f(x) 梯度是 Ax+b, Hesse 矩阵等于 A。
1.3 Jacobi 矩阵
Jacobi 矩阵实际上是向量值函数的梯度矩阵,假设F:Rn→Rm 是一个从n维欧氏空间转换到m维欧氏空间的函数。这个函数由m个实函数组成:
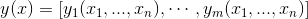
。这些函数的偏导数(如果存在)可以组成一个m行n列的矩阵(m by n),这就是所谓的雅可比矩阵:
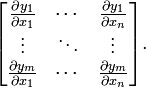
二、机器学习的优化算法
2.1 梯度下降法(Gradient Descent)
梯度下降法是最常用的一种优化算法,通过迭代地沿着梯度的负方向来寻找最优解。
在机器学习中,梯度下降法通常用于求解损失函数的最小值,通过不断更新模型的参数来逐渐减小损失函数的值。
梯度下降法的优点是简单、稳定且容易实现,适用于大规模数据集和复杂的模型。
梯度下降是一个大类,常见的梯度下降类算法如下图:
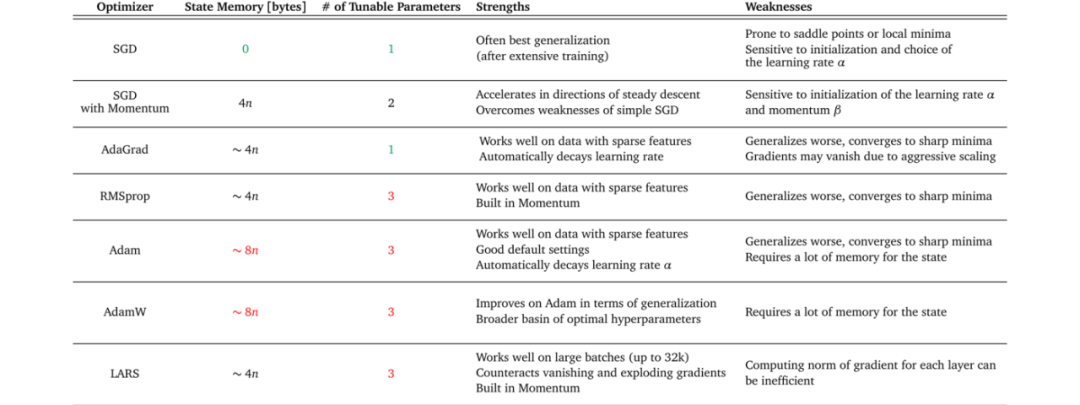
2.2 随机梯度下降法(Stochastic Gradient Descent, SGD)
随机梯度下降是在梯度下降算法效率上做了优化,不使用全量样本计算当前的梯度,而是使用小批量(mini-batch)样本来估计梯度,大大提高了效率。
原因在于使用更多样本来估计梯度的方法的收益是低于线性的,对于大多数优化算法基于梯度下降,如果每一步中计算梯度的时间大大缩短,则它们会更快收敛。且训练集通常存在冗余,大量样本都对梯度做出了非常相似的贡献。此时基于小批量样本估计梯度的策略也能够计算正确的梯度,但是节省了大量时间。
SGD具有快速收敛的特点,适用于处理大规模数据集和分布式计算环境。
SGD的缺点是容易陷入局部最优解,可结合其他优化算法如动量法或Adam等来提高收敛效果。
import numpy as np
# 定义损失函数
def loss_function(w, X, y):
return np.sum(np.square(X.dot(w) - y)) / len(y)
# 定义梯度函数
def gradient(w, X, y):
return X.T.dot((X.dot(w) - y)) / len(y)
# 定义SGD优化器
def sgd(X, y, learning_rate=0.01, epochs=100):
n_features = X.shape[1]
w = np.zeros(n_features)
for epoch in range(epochs):
for i in range(len(X)):
grad = gradient(w, X[i], y[i])
w -= learning_rate * grad
print("Epoch %d loss: %f" % (epoch+1, loss_function(w, X, y)))
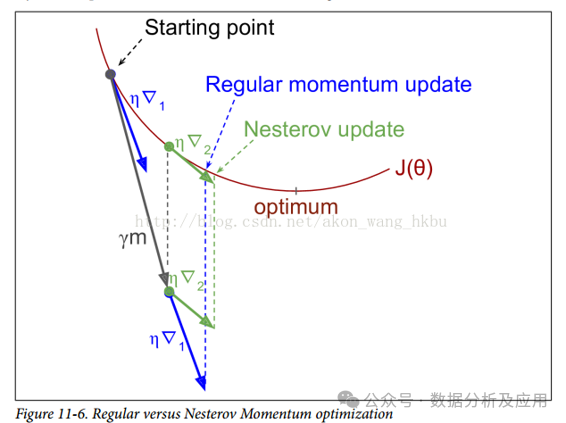
return w2.3 动量法(Momentum)和Nesterov 动量法
动量法通过引入一个动量项来加速梯度下降法的收敛速度。
Nesterov 动量法是对动量法的改进,在每一步迭代中考虑了未来的信息,从而更好地指导参数的更新方向。
动量法和Nesterov 动量法适用于非凸优化问题,能够跳出局部最优解并加速收敛。
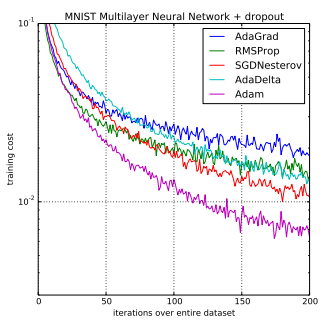
2.4 Adam(Adaptive Moment Estimation)
Adam是最常用的优化算法之一,是一种自适应学习率的优化算法,结合了动量法和RMSprop的思想。

Adam能够自动调整学习率,并且在不同的数据分布和模型结构下具有良好的收敛效果。(虽然说已经简化了调参,但是并没有一劳永逸地解决问题,默认的参数虽然好,但也不是放之四海而皆准。因此,在充分理解数据的基础上,依然需要根据数据特性、算法特性进行充分的调参实验。)
Adam适用于处理高维特征和稀疏数据集,非常适用于深度学习模型中的参数优化。在使用大型模型和数据集的情况下,Adam 优化算法在解决局部深度学习问题上是很高效的。
import torch
import torch.optim as optim
import numpy as np
# 定义损失函数和梯度函数(这里使用PyTorch的自动梯度计算)
loss_function = torch.nn.MSELoss() # 均方误差损失函数
gradient = torch.autograd.grad # 自动梯度计算函数
# 定义Adam优化器(这里使用了PyTorch的Adam类)
optimizer = optim.Adam([torch.Tensor([0.])], lr=0.01) # 学习率设置为0.01,初始权重为0向量(注意:PyTorch中优化器的权重参数需要是tensor对象)
optimizer.zero_grad() # 清除历史梯度信息(如果使用其他优化器,可能需要手动清除梯度)
output = loss_function(torch.Tensor([1]), torch.Tensor([[1, 2], [3, 4]]), torch.Tensor([[2], [4]])) # 计算损失函数值(这里使用了PyTorch的Tensor类,模拟了线性回归问题的数据和目标)
output.backward() # 反向传播计算梯度(这里使用了PyTorch的backward方法)
optimizer.step() # 更新权重(这里使用了PyTorch的step方法)2.5 AdaGrad(Adaptive Gradient Algorithm)和RMSprop
AdaGrad是一种自适应学习率的优化算法,能够根据参数的历史梯度来动态调整学习率。
RMSprop则是对AdaGrad的改进,通过引入一个指数衰减的平均来平滑历史梯度的方差。
AdaGrad和RMSprop适用于处理稀疏数据集和具有非平稳目标函数的优化问题。
2.6 牛顿法(Newton's Method)和拟牛顿法(Quasi-Newton Methods)
牛顿法是一种基于目标函数的二阶导数信息的优化算法,通过构建二阶导数矩阵并对其进行求解来逼近最优解。
拟牛顿法是牛顿法的改进,通过构造一个对称正定的矩阵来逼近目标函数的二阶导数矩阵的逆矩阵,从而避免了直接计算二阶导数矩阵的逆矩阵。
牛顿法和拟牛顿法适用于二阶可导的目标函数,具有较快的收敛速度,但在计算二阶导数矩阵时需要较大的存储空间。
import numpy as np
from scipy.linalg import inv
# 定义损失函数和Hessian矩阵
def loss_function(w, X, y):
return np.sum(np.square(X.dot(w) - y)) / len(y)
def hessian(w, X, y):
return X.T.dot(X) / len(y)
# 定义牛顿法优化器
def newton(X, y, learning_rate=0.01, epochs=100):
n_features = X.shape[1]
w = np.zeros(n_features)
for epoch in range(epochs):
H = hessian(w, X, y)
w -= inv(H).dot(gradient(w, X, y))
print("Epoch %d loss: %f" % (epoch+1, loss_function(w, X, y)))
return w2.7 共轭梯度法(Conjugate Gradient)
共轭梯度法是介于梯度下降法和牛顿法之间的一种方法,利用共轭方向进行搜索。
共轭梯度法的优点是在每一步迭代中不需要计算完整的梯度向量,而是通过迭代的方式逐步逼近最优解。
该方法适用于大规模问题,尤其是稀疏矩阵和对称正定的问题。
2.8 LBFGS(Limited-memory Broyden–Fletcher–Goldfarb–Shanno)
一种有限内存的Broyden-Fletcher-Goldfarb-Shanno(BFGS)算法,主要用于解决大规模优化问题。由于它只需要有限数量的计算机内存,因此特别适合处理大规模问题。LBFGS算法的目标是最小化一个给定的函数,通常用于机器学习中的参数估计。
import numpy as np
from scipy.optimize import minimize
# 目标函数
def objective_function(x):
return x**2 - 4*x + 4
# L-BFGS算法求解最小值
result = minimize(objective_function, x0=1, method='L-BFGS-B')
x_min = result.x
print(f"L-BFGS的最小值为:{objective_function(x_min)}")2.9 SA(Simulated Annealing)
一种随机搜索算法,其灵感来源于物理退火过程。该算法通过接受或拒绝解的移动来模拟退火过程,以避免陷入局部最优解并寻找全局最优解。在模拟退火算法中,接受概率通常基于解的移动的优劣和温度的降低,允许在搜索过程中暂时接受较差的解,这有助于跳出局部最优,从而有可能找到全局最优解。
import numpy as np
from scipy.optimize import anneal
# 目标函数
def objective_function(x):
return (x - 2)**2
# SA算法求解最小值
result = anneal(objective_function, x0=0, lower=-10, upper=10, maxiter=1000)
x_min = result.x
print(f"SA的最小值为:{objective_function(x_min)}")2.10 AC-SA(Adaptive Clustering-based Simulated Annealing)
一种基于自适应聚类的模拟退火算法。通过模拟物理退火过程,利用聚类技术来组织解空间并控制解的移动。该方法适用于处理大规模、高维度的优化问题,尤其适用于那些具有多个局部最优解的问题。
遗传算法是一种基于自然选择和遗传学机理的生物进化过程的模拟算法,适用于解决优化问题,特别是组合优化问题。该算法通过数学的方式,利用计算机仿真运算,将问题的求解过程转换成类似生物进化中的染色体基因的交叉、变异等过程。在求解较为复杂的组合优化问题时,相对一些常规的优化算法,通常能够较快地获得较好的优化结果。
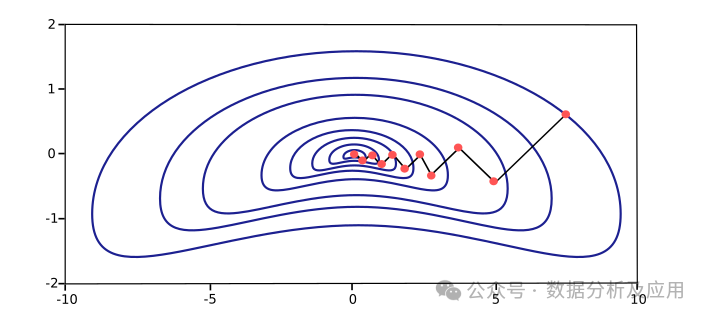
2.11 PSO(Particle Swarm Optimization)
PSO是一种基于种群的随机优化技术,模拟了鸟群觅食的行为(吐槽下,智能优化算法的领域真是卷麻了!!!)。粒子群算法模仿昆虫、兽群、鸟群和鱼群等的群集行为,这些群体按照一种合作的方式寻找食物,群体中的每个成员通过学习它自身的经验和其他成员的经验来不断改变其搜索模式。PSO算法适用于处理多峰函数和离散优化问题,具有简单、灵活和容易实现的特点。
回顾下各类算法的优缺点:
- 梯度下降类的优化算法:优点是简单、快速,常用于深度神经网络模型;缺点是可能得到的是局部最优解。
- 牛顿法:优点是二阶收敛,收敛速度快;缺点是需要计算目标函数的Hessian矩阵,计算复杂度高。
- 模拟退火算法:优点是避免陷入局部最优解,能够找到全局最优解;缺点是收敛速度慢,需要大量时间。
- 遗传算法:优点是通过变异机制避免陷入局部最优解,搜索能力强;缺点是编程复杂,需要设置多个参数,实现较为复杂。
- 粒子群优化算法:优点是简单、收敛快、计算复杂度低;缺点是多样性丢失、容易陷入局部最优,实现较为复杂。
三、优化算法的小结
本文介绍了梯度下降类、牛顿法、模拟退火、遗传算法和粒子群优化等常用的机器学习优化算法。这些算法各有特点和适用范围,选择合适的算法需要根据具体的问题、数据集和模型来进行权衡的。
最后,结合经验分享一些常用梯度下降类优化算法的选择和使用技巧:
首先,没有一种算法是普遍适用于所有情况的。如果你是初学者,建议从SGD+Nesterov Momentum或Adam开始。
选择你熟悉的算法,这样你可以更熟练地调整参数并利用经验。
充分了解你的数据。如果模型非常稀疏,优先考虑使用自适应学习率的算法。
根据你的需求选择算法。在模型设计实验阶段,为了快速验证新模型的效果,可以使用Adam进行快速实验优化。在模型上线或发布之前,使用经过微调的SGD进行模型的精细优化。
先用小数据集进行实验。有研究指出,随机梯度下降算法的收敛速度与数据集的大小关系不大。因此,可以使用具有代表性的小数据集进行实验,测试最佳优化算法,并通过参数搜索找到最优的训练参数。
考虑不同算法的组合。先用Adam进行快速下降,然后再切换到SGD进行充分调优。切换策略可以参考本文介绍的方法。
确保数据集充分打散(shuffle)。这样在使用自适应学习率算法时,可以避免某些特征集中出现,导致学习过度或不足,使下降方向出现偏差。
在训练过程中持续监控训练数据和验证数据上的目标函数值以及精度或AUC等指标的变化情况。对训练数据的监控是为了确保模型进行了充分训练——下降方向正确且学习率足够高。对验证数据的监控是为了避免过拟合。
制定合适的学习率衰减策略。可以使用定期衰减策略,例如每过几个epoch就衰减一次;或者利用精度或AUC等性能指标进行监控。当测试集上的指标不再改善或下降时,降低学习率。