我们人类可能要养不起AI了!
近日,来自MIT FutureTech的研究人员发表了一项关于大模型能力增长速度的研究,
结果表明:LLM的能力大约每8个月就会翻一倍,速度远超摩尔定律!

论文地址:https://arxiv.org/pdf/2403.05812.pdf
LLM的能力提升大部分来自于算力,而摩尔定律代表着硬件算力的发展,
——也就是说,随着时间的推移,终有一天我们将无法满足LLM所需要的算力!
如果那个时候AI有了意识,不知道会不会自己想办法找饭吃?
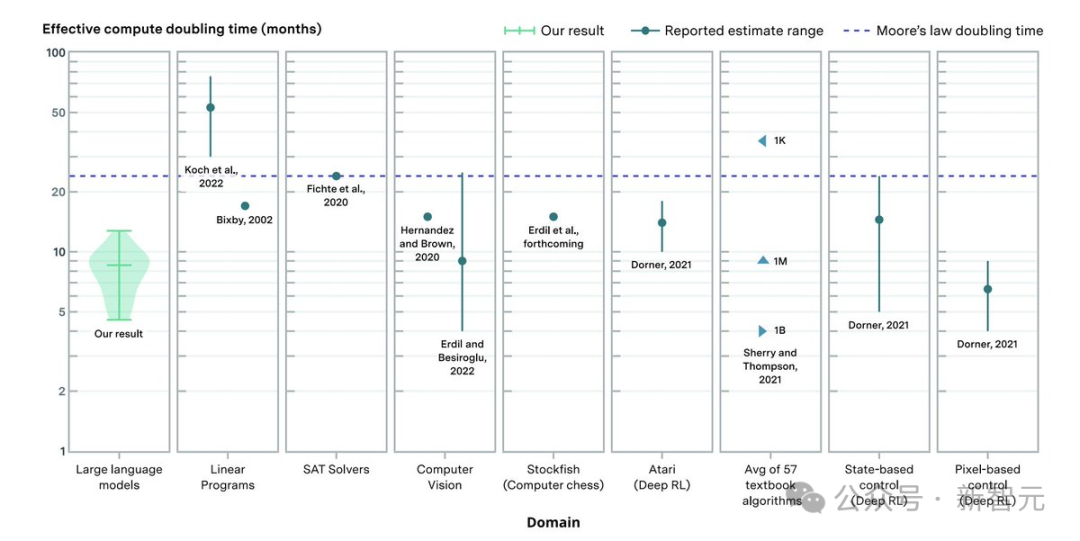
上图表示不同领域的算法改进对有效计算翻倍的估计。蓝点表示中心估计值或范围;蓝色三角形对应于不同大小(范围从1K到1B)的问题的倍增时间;紫色虚线对应于摩尔定律表示的2年倍增时间。
摩尔定律和比尔盖茨
摩尔定律(Moore's law)是一种经验或者观察结果,表示集成电路(IC)中的晶体管数量大约每两年翻一番。
1965年,仙童半导体(Fairchild Semiconductor)和英特尔的联合创始人Gordon Moore假设集成电路的组件数量每年翻一番,并预测这种增长率将至少再持续十年。

1975年,展望下一个十年,他将预测修改为每两年翻一番,复合年增长率(CAGR)为41%。
虽然Moore没有使用经验证据来预测历史趋势将继续下去,但他的预测自1975年以来一直成立,所以也就成了“定律”。
因为摩尔定律被半导体行业用于指导长期规划和设定研发目标,所以在某种程度上,成了一种自我实现预言。
数字电子技术的进步,例如微处理器价格的降低、内存容量(RAM 和闪存)的增加、传感器的改进,甚至数码相机中像素的数量和大小,都与摩尔定律密切相关。
数字电子的这些持续变化一直是技术和社会变革、生产力和经济增长的驱动力。
不过光靠自我激励肯定是不行的,虽然行业专家没法对摩尔定律能持续多久达成共识,但根据微处理器架构师的报告,自2010年左右以来,整个行业的半导体发展速度已经放缓,略低于摩尔定律预测的速度。
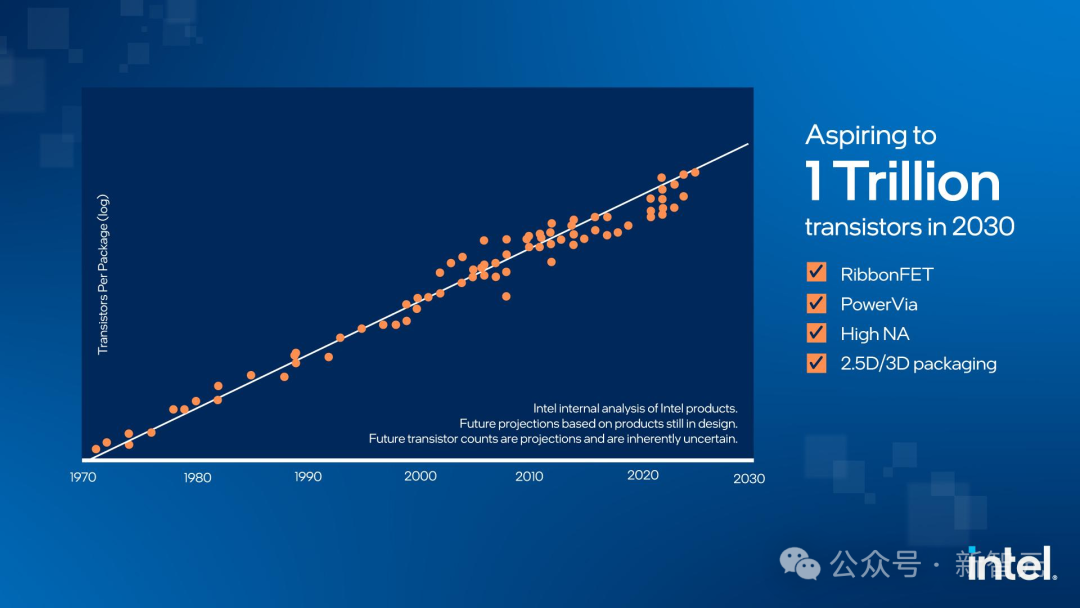
下面是维基百科给出的晶体管数量增长趋势图:
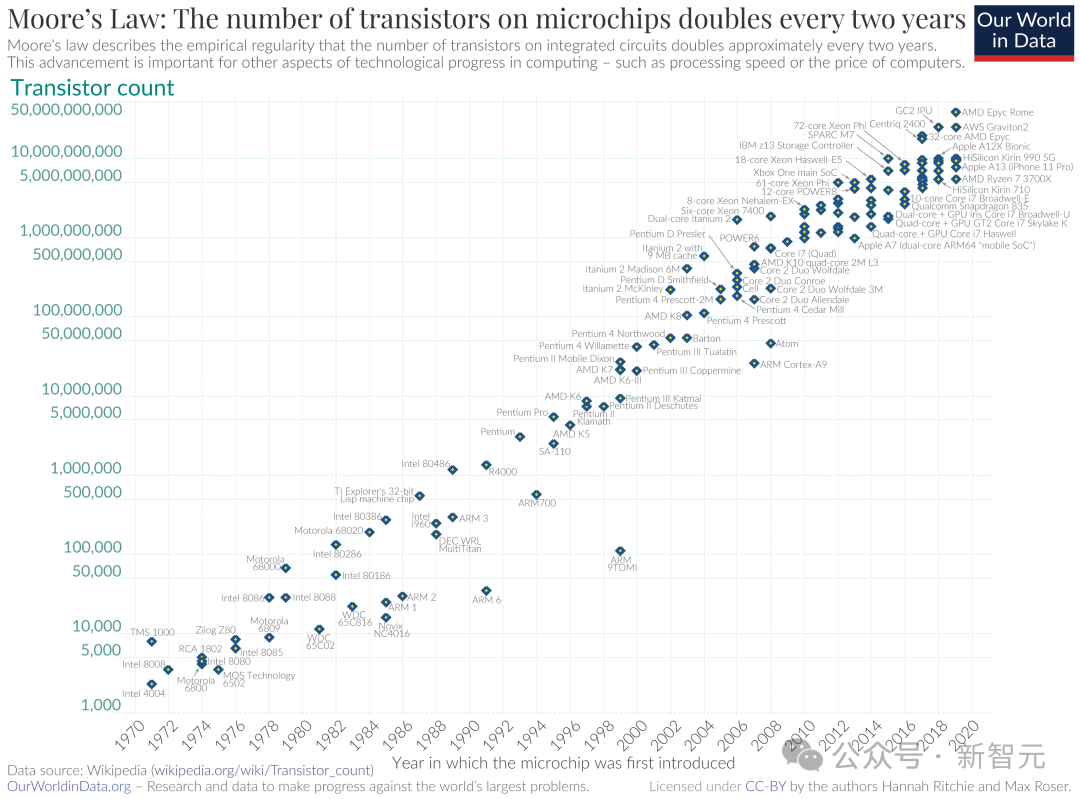
到了2022年9月,英伟达首席执行官黄仁勋直言“摩尔定律已死”,不过英特尔首席执行官Pat Gelsinger则表示不同意。
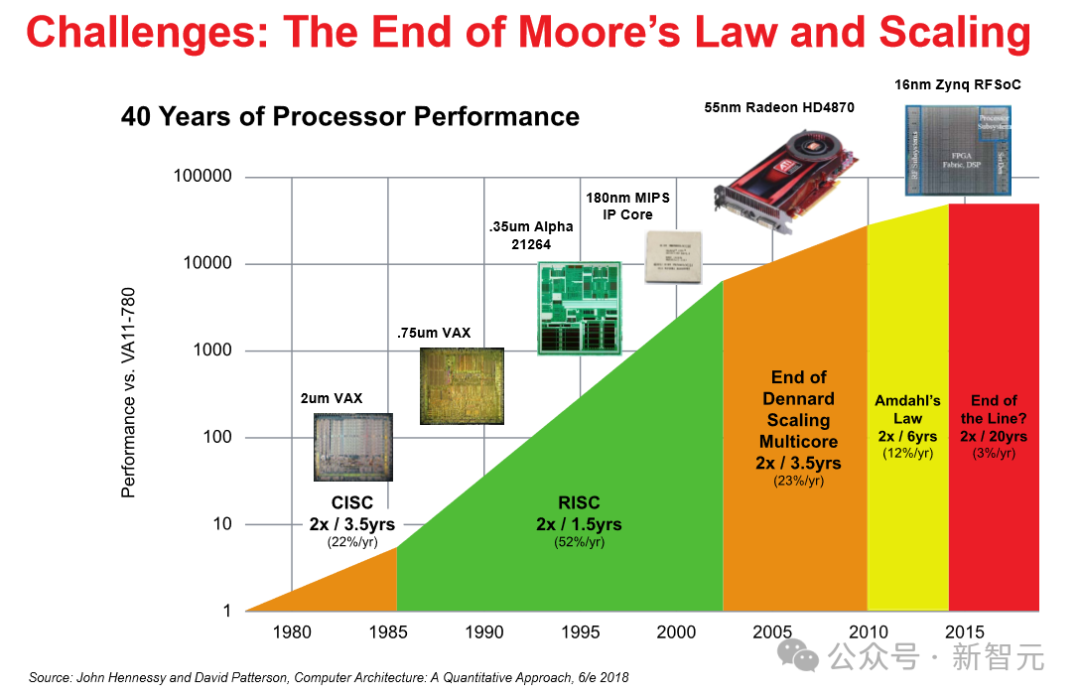
从下图我们可以看出,英特尔还在努力用各种技术和方法为自己老祖宗提出的定律续命,并表示,问题不大,你看我们还是直线没有弯。
Andy and Bill's Law
关于算力的增长,有一句话是这样说的:“安迪给的,比尔都拿走(What Andy giveth, Bill taketh away)”。

这反映了当时的英特尔首席执行官Andy Grove每次向市场推出新芯片时,微软的CEO比尔·盖茨(Bill Gates)都会通过升级软件来吃掉芯片提升的性能。
——而以后吃掉芯片算力的就是大模型了,而且根据MIT的这项研究,大模型以后根本吃不饱。
研究方法
如何定义LLM的能力提升?首先,研究人员对模型的能力进行了量化。
基本的思想就是:如果一种算法或架构在基准测试中以一半的计算量获得相同的结果,那么就可以说,它比另一种算法或架构好两倍。
有了比赛规则之后,研究人员招募了200多个语言模型来参加比赛,同时为了确保公平公正,比赛所用的数据集是WikiText-103和WikiText-2以及Penn Treebank,代表了多年来用于评估语言模型的高质量文本数据。
专注于语言模型开发过程中使用的既定基准,为比较新旧模型提供了连续性。
需要注意的是,这里只量化了预训练模型的能力,没有考虑一些“训练后增强”手段,比如思维链提示(COT)、微调技术的改进或者集成搜索的方法(RAG)。
模型定义
研究人员通过拟合一个满足两个关键目标的模型来评估其性能水平:
(1)模型必须与之前关于神经标度定律的工作大致一致;
(2)模型应允许分解提高性能的主要因素,例如提高模型中数据或自由参数的使用效率。
这里采用的核心方法类似于之前提出的缩放定律,将Dense Transformer的训练损失L与其参数N的数量和训练数据集大小D相关联:
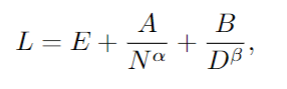
其中L是数据集上每个token的交叉熵损失,E、A、B、α和β是常数。E表示数据集的“不可减少损失”,而第二项和第三项分别代表由于模型或数据集的有限性而导致的错误。
因为随着时间的推移,实现相同性能水平所需的资源(N 和 D)会减少。为了衡量这一点,作者在模型中引入了“有效数据”和“有效模型大小”的概念:
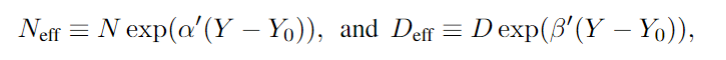
其中的Y表示年份,前面的系数表示进展率,代入上面的缩放定律,可以得到:
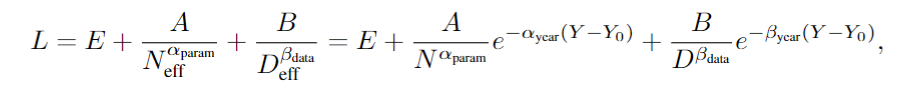
通过这个公式,就可以估计随着时间的推移,实现相同性能水平所需的更少资源(N和D)的速度。
数据集
参与测评的包含400多个在WikiText-103(WT103)、WikiText-2(WT2)和Penn Treebank(PTB)上评估的语言模型,其中约60%可用于分析。
研究人员首先从大约200篇不同的论文中检索了相关的评估信息,又额外使用框架执行了25个模型的评估。
然后,考虑数据的子集,其中包含拟合模型结构所需的信息:token级测试困惑度(决定交叉熵损失)、发布日期、模型参数数量和训练数据集大小,最终筛选出231个模型供分析。
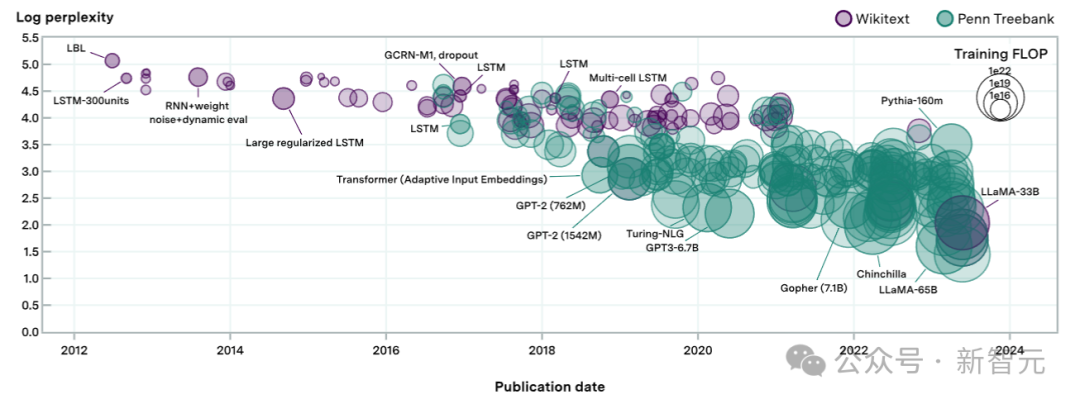
这231个语言模型,跨越了超过8个数量级的计算,上图中的每个形状代表一个模型。
形状的大小与训练期间使用的计算成正比,困惑度评估来自于现有文献以及作者自己的评估测试。
在某些情况下,会从同一篇论文中检索到多个模型,为了避免自相关带来的问题,这里每篇论文最多只选择三个模型。
实证结果
根据缩放定律,以及作者引入的有效数据、有效参数和有效计算的定义来进行评估,结果表明:有效计算的中位倍增时间为8.4个月,95%置信区间为4.5至14.3个月。
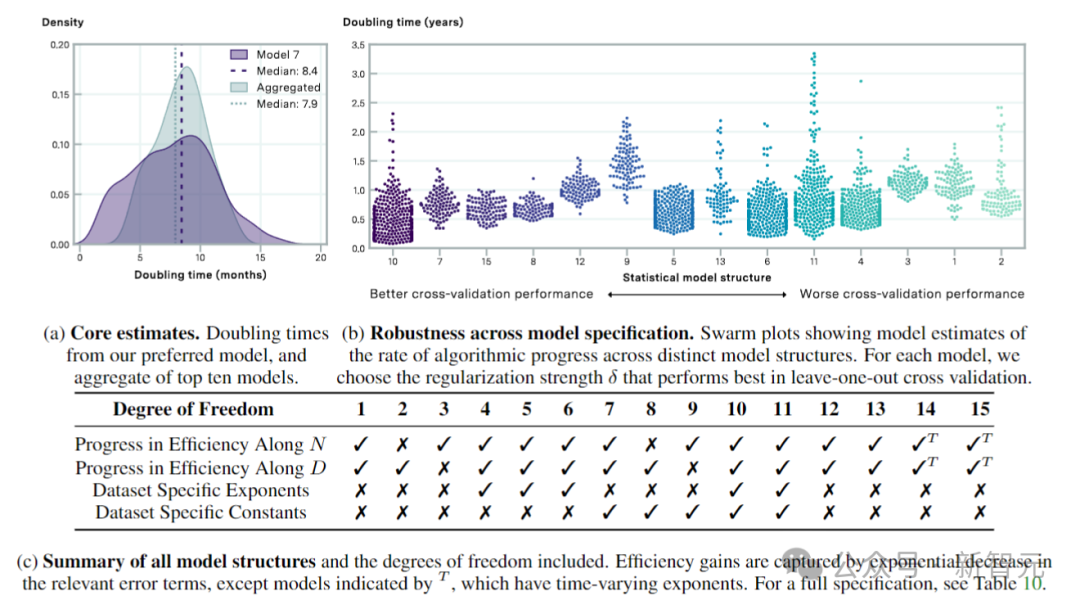
上图表示通过交叉验证选择的模型的算法进度估计值。图a显示了倍增时间的汇总估计值,图b显示了从左到右按交叉验证性能递减(MSE测试损耗增加)排序。
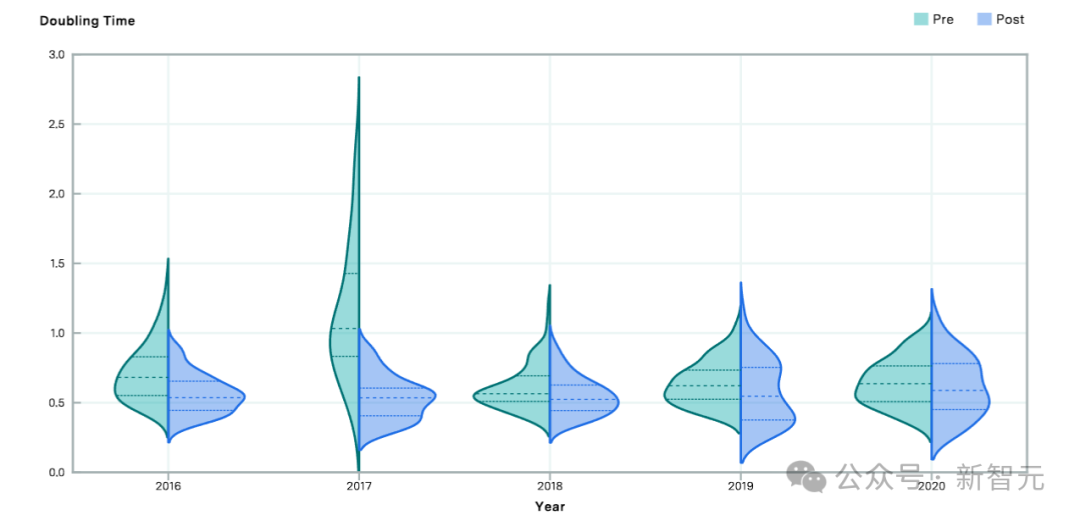
上图比较了2016年至2020年前后的算法有效计算的估计倍增时间。相对于前期,后期的倍增时间较短,表明在该截止年之后算法进步速度加快。