合成数据持续解锁大模型的数学推理潜力!
数学问题解决能力一直被视为衡量语言模型智能水平的重要指标。通常只有规模极大的模型或经过大量数学相关预训练的模型才能有机会在数学问题上表现出色。
近日,一项由 Swin-Transformer 团队打造,来自西安交通大学、中国科学技术大学、清华大学和微软亚洲研究院的学者共同完成的研究工作 Xwin 颠覆了这一认知,揭示了通用预训练下 7B(即 70 亿参数)规模的语言模型(LLaMA-2-7B)在数学问题解决方面已经展现出较强的潜力,并可使用基于合成数据的有监督微调方法促使模型愈发稳定地将数学能力激发出来。
这项研究发布在 arXiv 上,题为《Common 7B Language Models Already Possess Strong Math Capabilities》。

- 论文链接:https://arxiv.org/pdf/2403.04706.pdf
- 代码链接:https://github.com/Xwin-LM/Xwin-LM
研究团队首先仅使用 7.5K 数据,对 LLaMA-2-7B 模型指令微调,进而测评模型在 GSM8K 和 MATH 的表现。实验结果表明,当对每一个测试集中的问题从 256 个生成的答案中选择最佳答案时,测试准确率可分别高达 97.7% 和 72.0%,这一结果说明即使是通用预训练下 7B 量级的小模型,也具备生成优质回答的巨大潜力,这一发现挑战了以往的观点,即强大的数学推理潜力并非仅限于大规模和数学相关预训练模型。
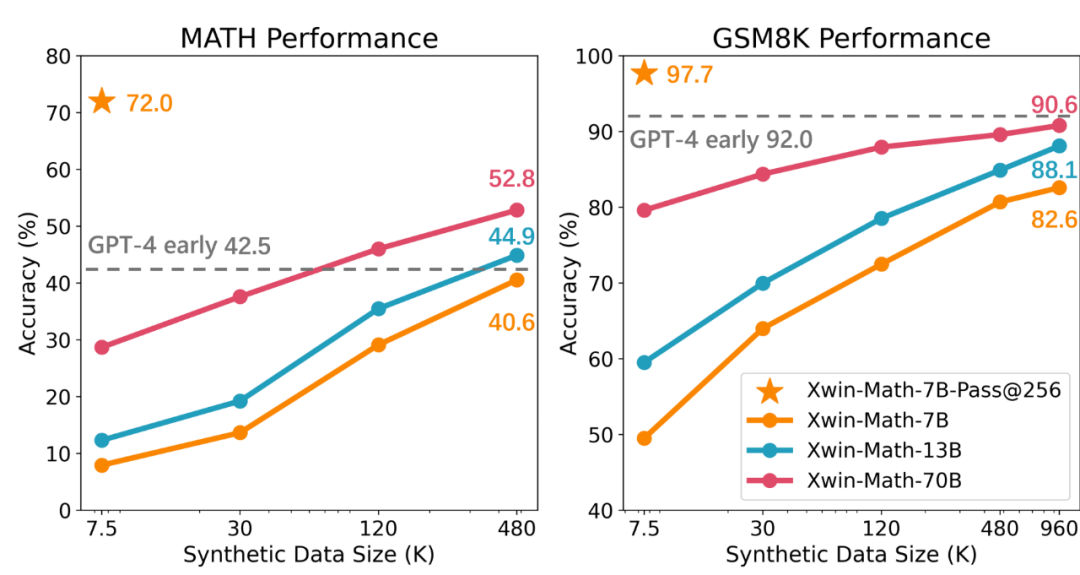
然而研究也指出,尽管已具备强大的数学推理潜力,但当前语言模型的主要问题是难以一致地激发其内在的数学能力。例如,在前面的实验中如果只考虑每个问题的一次生成的答案,那么在 GSM8K 和 MATH 基准测试上的准确率会分别降至 49.5% 和 7.9%。这体现出模型数学能力的不稳定性问题。为了解决这一问题,研究团队采用了扩大有监督微调(SFT)数据集的方法,并发现随着 SFT 数据的增多,模型生成正确答案的可靠性被显著提升。
研究中还提到,通过使用合成数据,可以有效地扩大 SFT 数据集,而且这种方法几乎与真实数据一样有效。研究团队利用 GPT-4 Turbo API 生成了合成的数学问题与解题过程,并通过简单的验证提示词来确保问题的质量。通过这种方法,团队成功地将 SFT 数据集从 7.5K 扩展到约一百万样本,实现了近乎完美的缩放定律(Scaling Law)。最终获得的 Xwin-Math-7B 模型在 GSM8K 和 MATH 上分别达到了 82.6% 和 40.6% 的准确率,大幅超越此前的 SOTA 模型,甚至可超越一些 70B 量级模型,实现越级提升。而 Xwin-Math-70B 模型在 MATH 评测集上的结果可达 52.8%,显著超越了 GPT-4 的早期版本。这是基于 LLaMA 系列基础模型的研究第一次在 MATH 上超越 GPT-4。
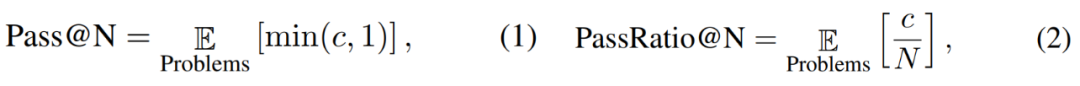
研究人员还定义了 Pass@N 和 PassRatio@N 评测指标,意图分别测评模型的 N 次输出中,是否能够输出正确答案(表示模型潜在的数学能力),以及正确答案的所占比例(表示模型数学能力的稳定性)。当 SFT 数据量较小时,模型的 Pass@256 已经很高,进一步扩大 SFT 数据规模后,模型的 Pass@256 提升极小,而 PassRatio@256 则获得显著增长。这表明基于合成数据的有监督微调是提升模型数学能力稳定性的有效方式。
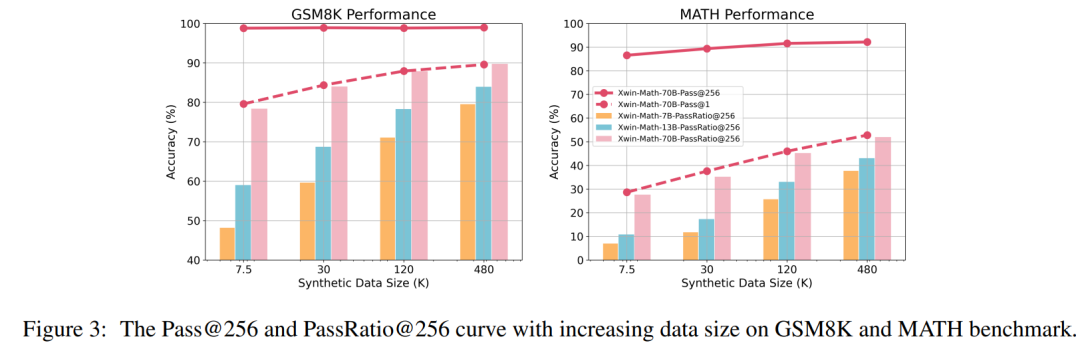
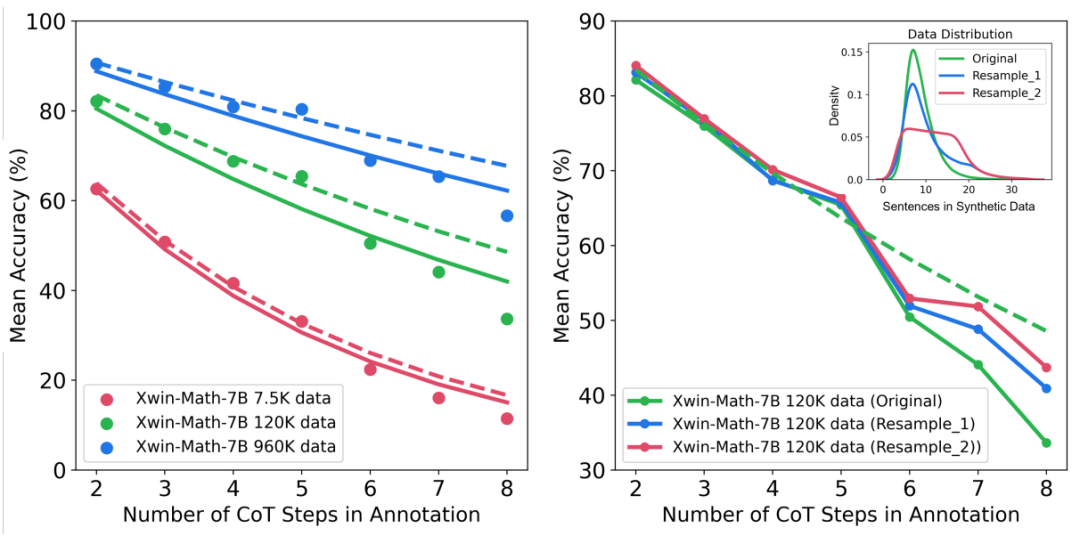
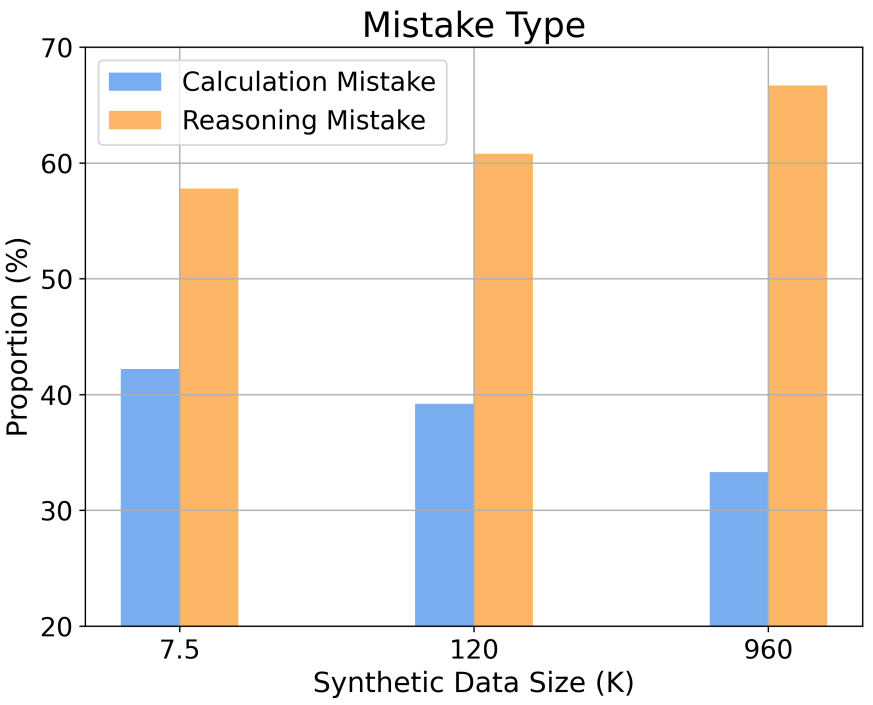
此外,研究还提供了对不同推理复杂性和错误类型下扩展行为的洞察。例如,随着 SFT 数据集规模的增加,模型在解决数学问题时的准确率遵循与推理步骤数量相关的幂律关系。通过增加训练样本中长推理步骤的比例,可以显著提高模型解决难题的准确率。同时,研究还发现,计算错误比推理错误更容易被缓解。
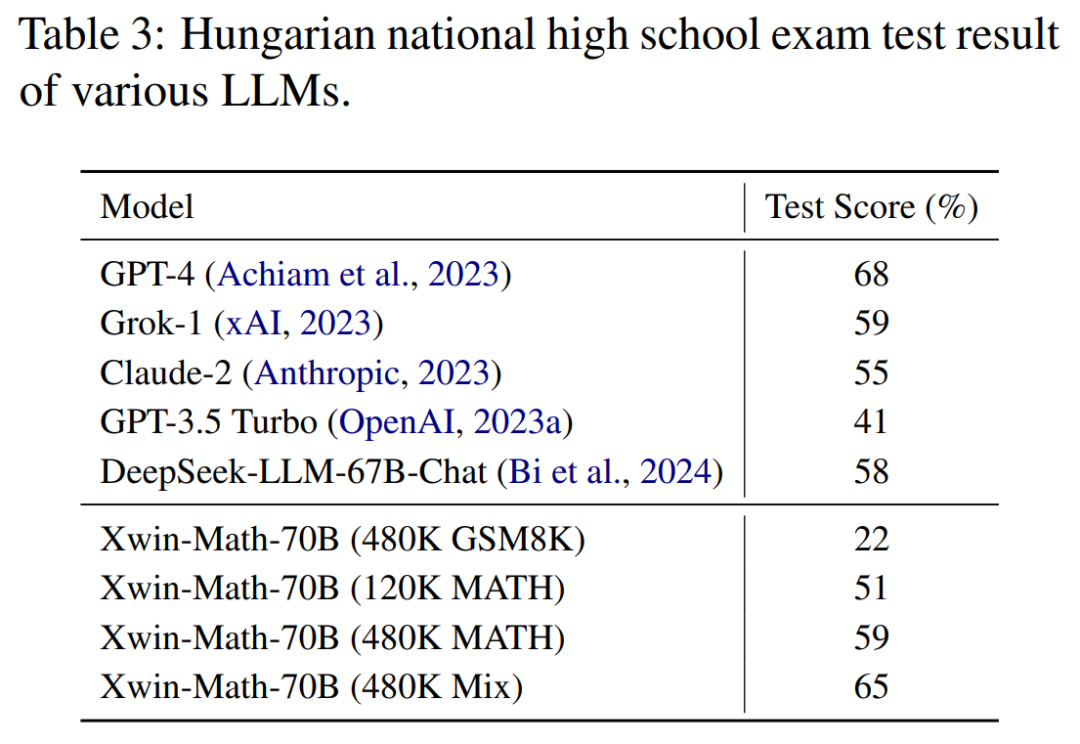
在表现模型数学推理泛化能力的匈牙利高中数学考试中,Xwin-Math 也拿到了 65% 的分数,仅次于 GPT-4。这表明研究中合成数据的方式并没有显著地过拟合到评测集中,展现出良好的泛化能力。

这项研究不仅展示了合成数据在扩展 SFT 数据方面的有效性,而且为大型语言模型在数学推理能力方面的研究提供了新的视角。研究团队表示,他们的工作为未来在这一领域的探索和进步奠定了基础,并期待能够推动人工智能在数学问题解决方面取得更大的突破。随着人工智能技术的不断进步,我们有理由期待 AI 在数学领域的表现将更加出色,为人类解决复杂数学问题提供更多帮助。










































