一、归因诊断
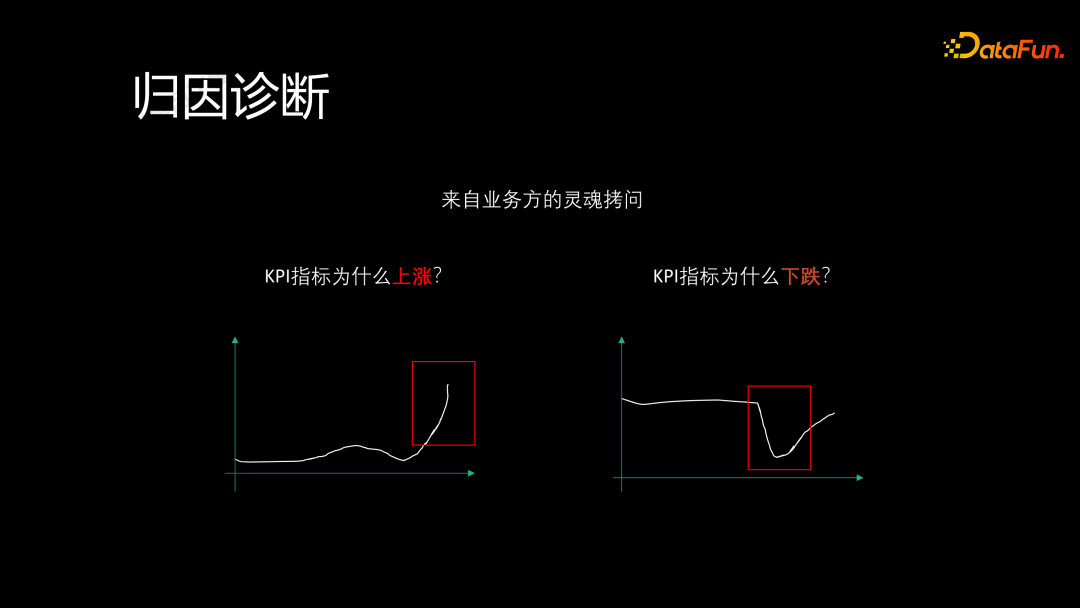
在实际工作中,我们常常受到业务方对关键绩效指标(KPI)的灵魂拷问:某个 KPI 指标为什么会上升或下降?归因诊断的任务就是解释这些指标变化的原因。
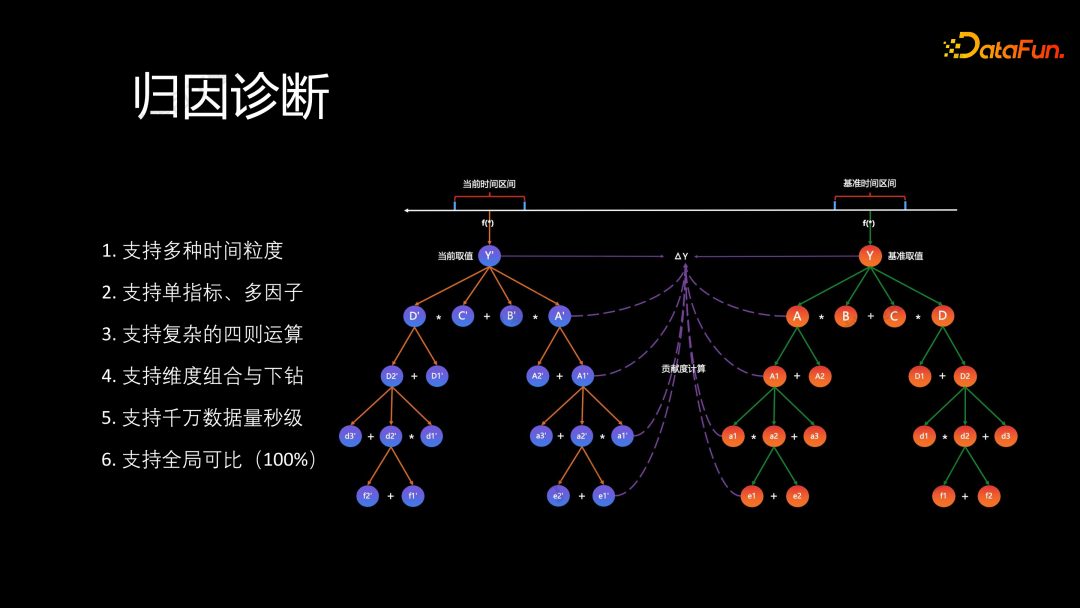
归因诊断把问题的定位过程看作是一个因子对比的过程:指标在基准时间区间的值为 y,在当前时间区间的值为 y^',两个时间点相差 ∆y。基于这个变化量 ∆y 进行因子的拆解,生成一个因子指标树。在每个叶子节点处,都计算其对整体 ∆y 的贡献度,从而确定哪个因子对整体贡献最大。
通过以上过程,就能够解释 KPI 波动的原因。在实际应用中,可以支持:
- 多时间粒度的对比,包括单天和多天的对比。
- 单指标的对比、多因子的归因以及复杂的四则运算。
- 维度的组合与下钻。
- 千万级数据量级上秒级的智能返回。
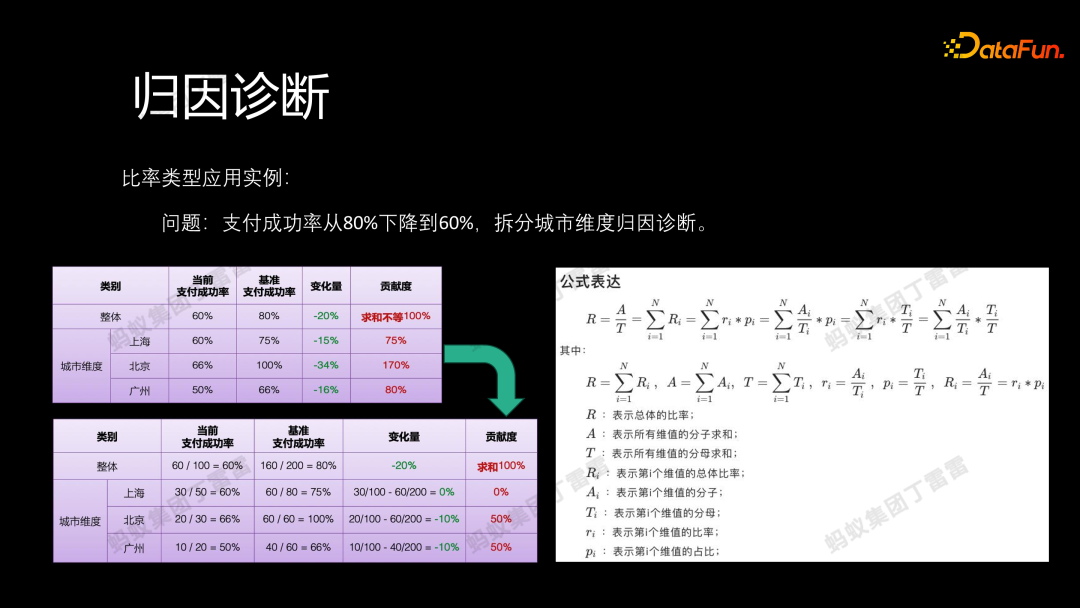
接下来举例说明上述归因过程。在实际业务中,假设支付成功率从 80% 下降到 60%,如果按照城市的维度,通过将变化量分配给各个城市从而进行归因诊断,即先计算上海 -15%,北京 -34%,广州 -16%。然后,将这些城市的变化量除以整体变化量(-20%),得到上海为支付成功率下降贡献了 75%,北京贡献了 170%,广州贡献了 80% 的结论。这样的计算方法是存在问题的,因为城市的贡献求和并不等于 100%。正确的逻辑应该是在计算每个城市的贡献时,考虑每个城市的分子分母的情况。因此,上海实际在支付成功率上没有变化,是一个分子分母等比率缩放的情况;而北京和广州则是都下降了10%,为整体变化量(-20%)各自贡献了 50%。
通过这样逐层拆解,可以清晰地看到每个因子对整体的贡献,解释具体的变化是由分子还是分母引起的,是由比率变化还是占比变化引起的。这种逐层拆解的逻辑为我们提供了一个全局可比的归因结论,有助于向业务做出清晰的解释。
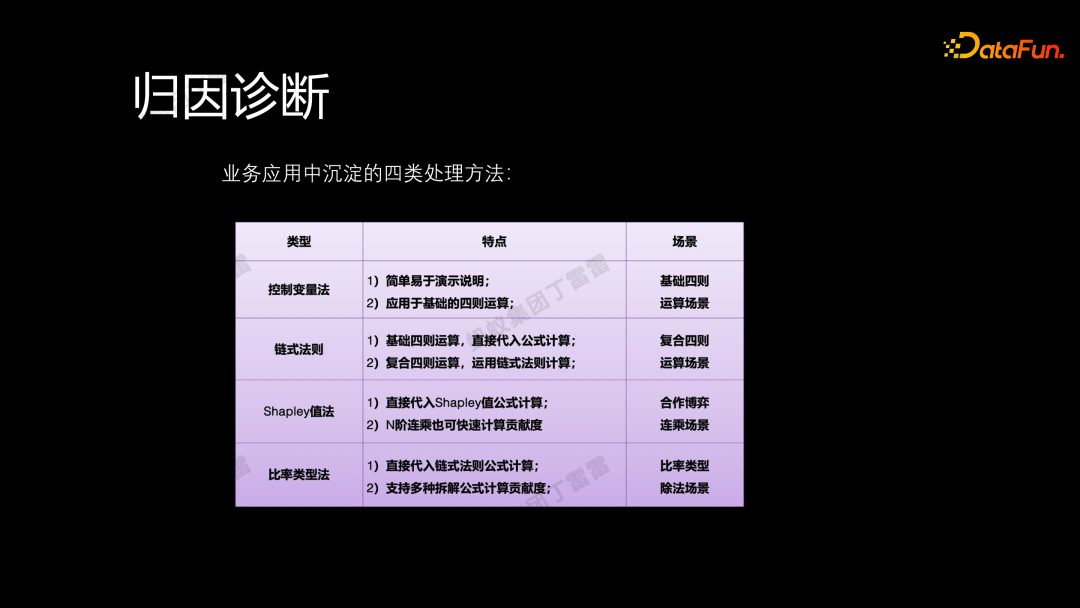
在实际应用中,我们总结出四类方法,用于处理不同的业务场景:
- 控制变量法,适用于简单的四则运算场景。
- 链式法则,可用于处理复杂的四则运算。
- Shapley 值法,适用于连乘场景,我们将其视为合作博弈问题来解决。
- 比率类型法(前文讲述的内容)。
这些方法在业务的实际应用中表现出色,取得了显著的效果。
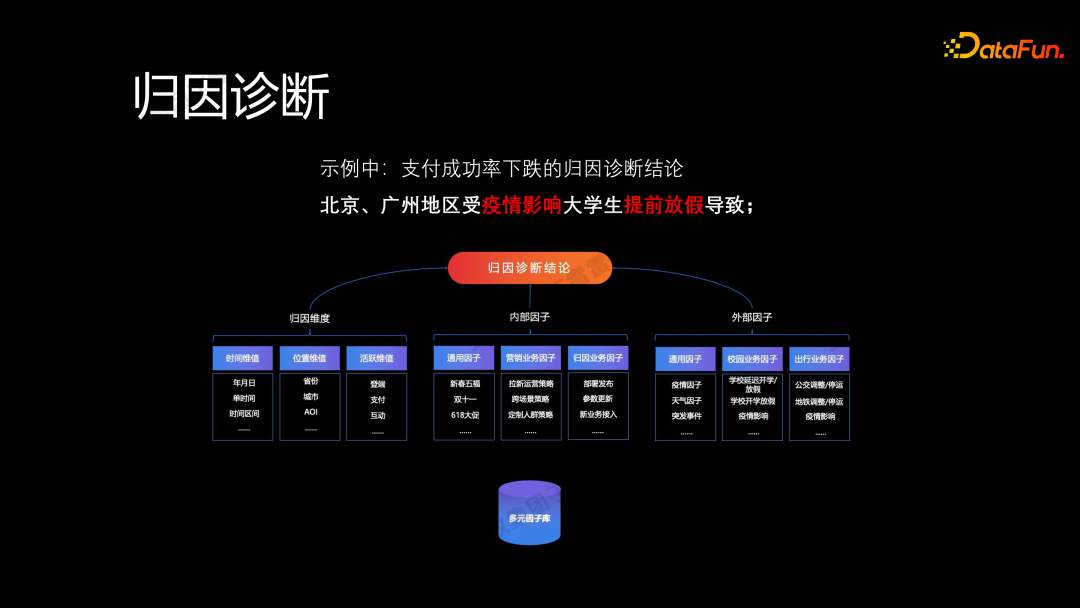
在刚刚的归因过程中,虽然将问题归因到城市维度,但并没有明确解释支付成功率下降的具体原因。因此,需要进一步对因子进行归因,主要分为三个部分:
- 首先是归因的维度,包括城市等。
- 其次是内部因子,如促销活动、营销手段以及运维场景中的一些动作。
- 最后是外部因子,包括通用因素,如疫情、天气、突发事件等,还包括特殊业务场景、出行场景等。
整个归因过程会生成一个多元因子库,基于这个库,我们重新审视支付成功率下降的问题,得出结论。例如,我们发现北京和广州的下降是因为受到疫情影响,大学生提前放假导致支付成功率下降。业务方得到这一结论后,可以做出相应的判断和策略调整,采取营销手段或其他措施,以解决支付成功率下降的问题,重新提升业务。
二、异常检测
1. 单指标异常检测

接下来介绍一下异常检测,首先从单指标异常检测入手。在实际业务中,业务方关心的是监控指标何时开始异常告警,以及异常告警何时结束。如果我们能够了解指标的正常波动区间,就能够解决这个问题,将告警信息实时、准确地反馈给业务方。
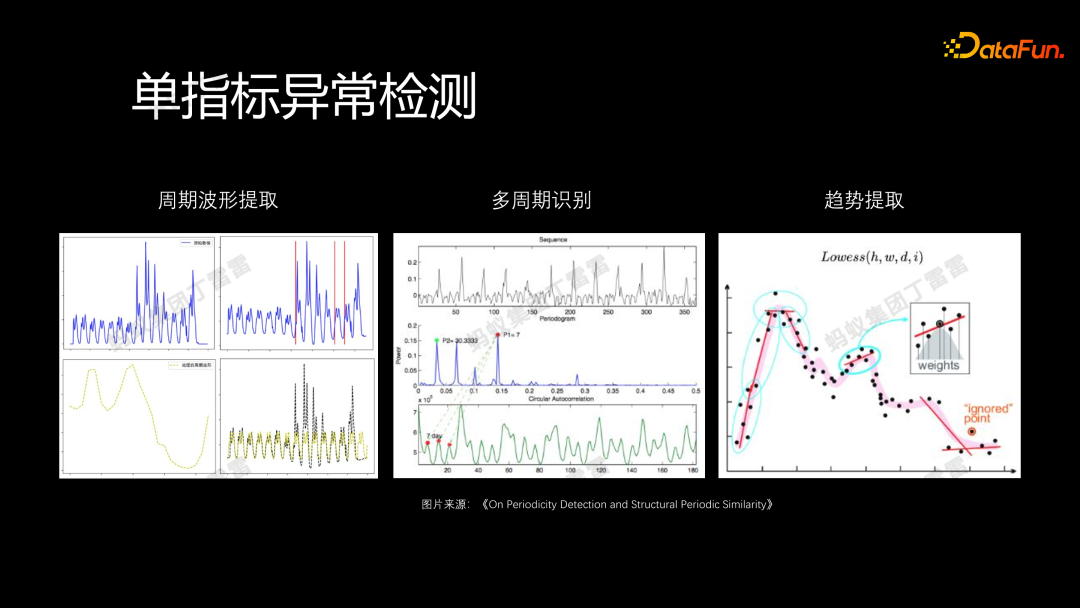
计算一个指标的正常波动区间可以借鉴 STL 时区分解的思路:
首先采用 STL 中通用的 lowess 函数进行趋势提取,同时提取周期信息,即识别时序中包含的周期以及周期的长度(例如,7 天、30 天、周、月、季度、年、小时等),这里我们借鉴论文中的 FFT 加 ACF 处理逻辑,可以识别出周期。
识别了周期后,下一步是提取周期波形。通过很好地提取周期波形并叠加周期,就能够有效地进行检测。
在提取周期波形时,由于周期波形受到营销活动的影响,振幅可能发生变化,因此还需要引入一些检测方法进行分段处理,最终获得相对完整的周期波形进行后续处理。
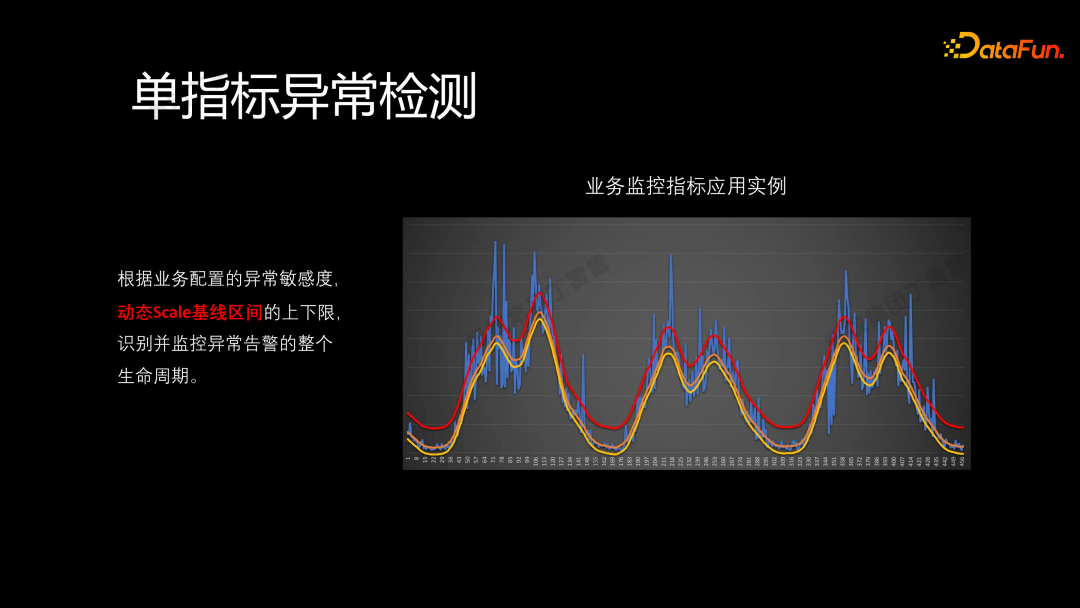
上图展示了一个真实案例:根据业务配置的异常敏感度动态调整基线的上下限,识别并监控异常告警的整个生命周期。我们能够清晰地追踪何时进入异常状态,以及何时恢复正常。整个过程都能够被有效监控。

在这个智能告警的案例中,当系统触发告警时,可以追溯到异常发生的时刻,随着告警持续推移,最终系统恢复正常,即自动关闭相应的告警单。这样一来,运维团队就不必花费过多精力处理那些自动关闭的告警,而能够集中精力处理更为紧急的运维任务。
在实际应用中,我们的系统在异常检测方面有着优异的表现:
- 支持多敏感度的调控,用户可以根据需要调整异常检测的敏感度,以求告警更少或更精准。
- 支持在线实时的反馈调优机制,用户可以通过打标告诉我们单子是否已经恢复,是否是误报或者是精准的,从而实时调整正常指标的波动区间。
- 支持无监督的增量指标接入,能够快速接入并实时进行检测。
- 系统支持全生命周期的监控,并能够毫秒级地处理,满足业务性能要求。
2. 多指标异常检测
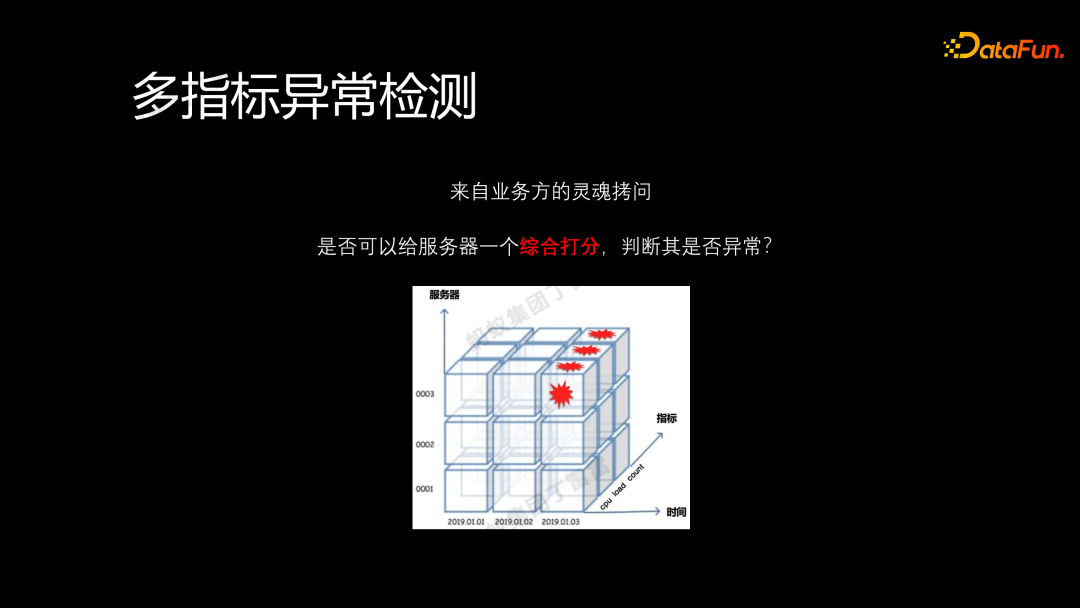
接下来介绍多指标异常检测的应用。在业务中,面对多个服务器每天产生大量的指标数据,业务方通常关心如何对每台服务器进行综合评分,以判断其是否异常。如图中,纵轴表示不同的服务器,每层代表一个服务器,横轴表示时间。随着时间的推移,每台服务器都会产生多个指标的数据值。

我们把这个问题定义一下:
- X^j:第 j 个服务器的时间序列数据矩阵。
- X ⃗_k^j:第 j 个服务器的第 k 个指标时序数据。
- X ⃗_ki^j:第 j 个服务器的第 k 个指标 i 时刻取值。
上述由时间序列构成的数据矩阵 X^j 能够全面描述一台服务器在每个时刻的状态。那么问题就转化成了:如果我们能够表征出一个整体评分,即为每台服务器 X^j 打一个分数,那么就能综合反映出该服务器是否出现异常。
接下来将介绍三种方法:
- VBEM 算法
- AnoSVGD 算法
- Autoformer 算法
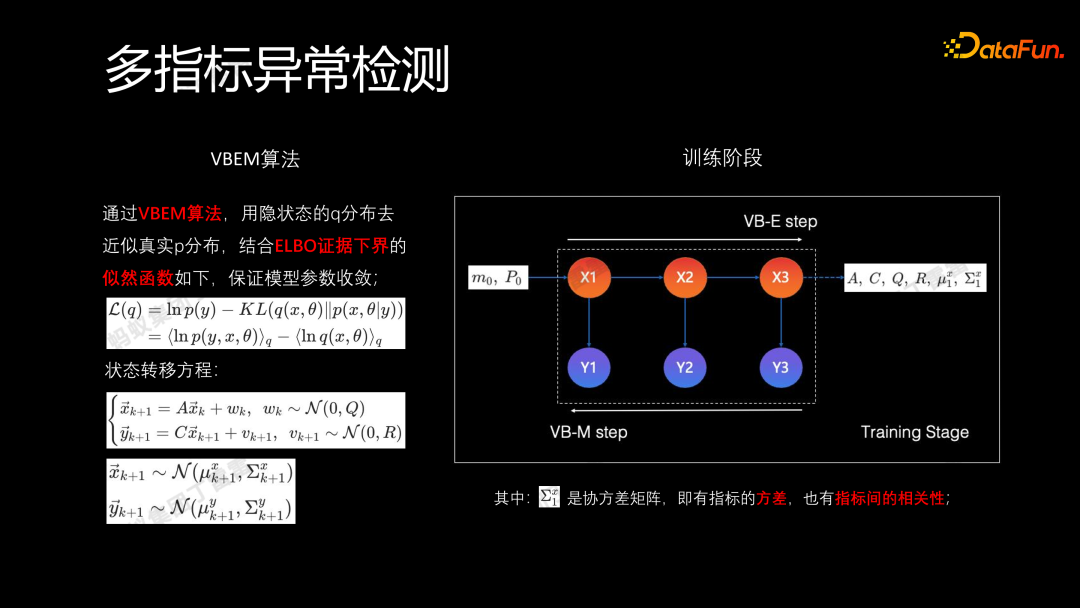
VBEM 是基于变分推断(Variational Inference)的期望最大化(Expectation-Maximization)算法。通过隐状态 q 分布来逼近真实后验 p 的分布,结合 ELBO 证据下接的似然函数保证模型参数的收敛,整个过程是一个状态转移过程。如图中,x_i 表示学习到的隐状态,m_0 和 P_0 是模型的初始参数(均值和斜方差)。最终要学到的参数是 A、C、Q、R、μ_1^x、Σ_1^x,分别对应状态转移中的权重、均值和协方差的分布,其中 Σ_1^x 是协方差矩阵,包含方差信息和指标之间的相关性,可以很好地表征多指标的信息。
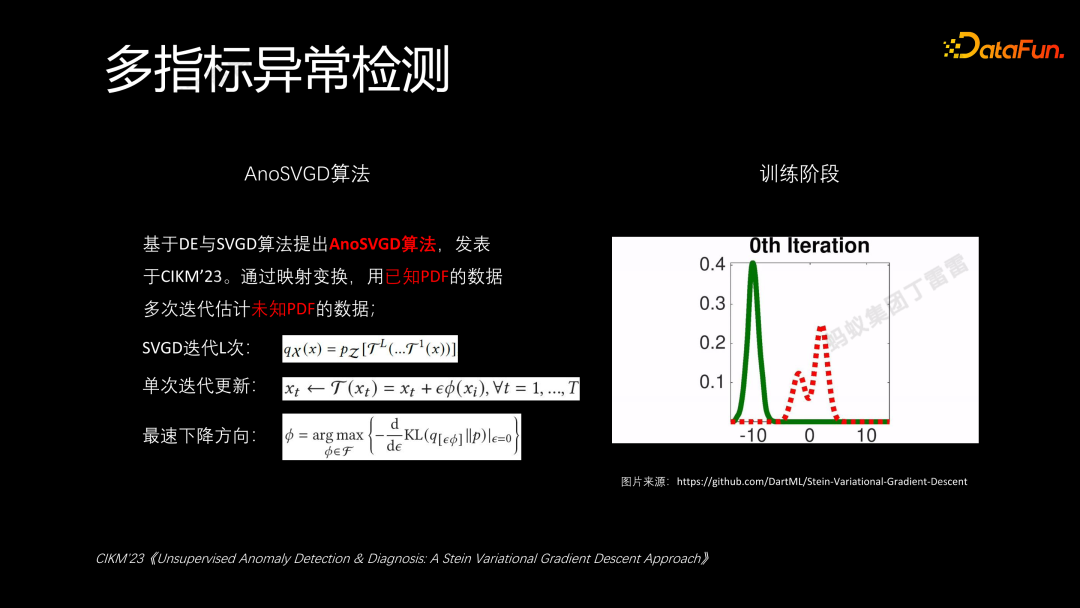
AnoSVGD 方法是我们在 CIKM 2023 年会议上发表的一篇论文。其核心思想是通过映射变换,用已知数据的概率密度函数(Probability Density Function,PDF),多次迭代估计未知数据的概率密度函数(PDF)。通过观察右侧的图可以看到,在多次迭代之后,模型能够有效地表征未知数据的分布。每次迭代时,基于前一次的结果,加上一个小的步长和下降方向 θ,通过梯度下降找到最快的下降方向,从而进行迭代。这样,我们能够快速地找到未知数据的分布,并在达到目标后停止迭代。
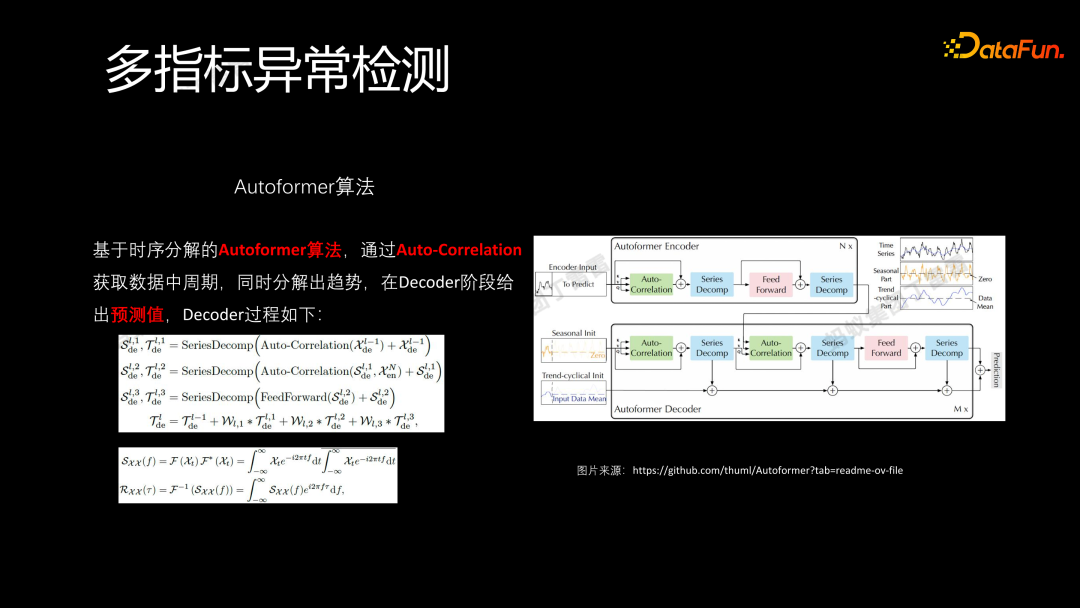
Autoformer 算法的核心在于采用了时序分解的思想,类似于 Transformer 中的self-attention 机制:
- Autoformer 通过 Auto-Correlation 获取数据中的周期信息。
- 有了周期信息,Autoformer 通过分解的方式将周期波形和趋势提取出来。
- 在 decoder 阶段,通过多次迭代输出预测值。这里计算 auto collaboration 时采用了与之前周期识别相一致的思想,即使用 FFT 和 ACF。
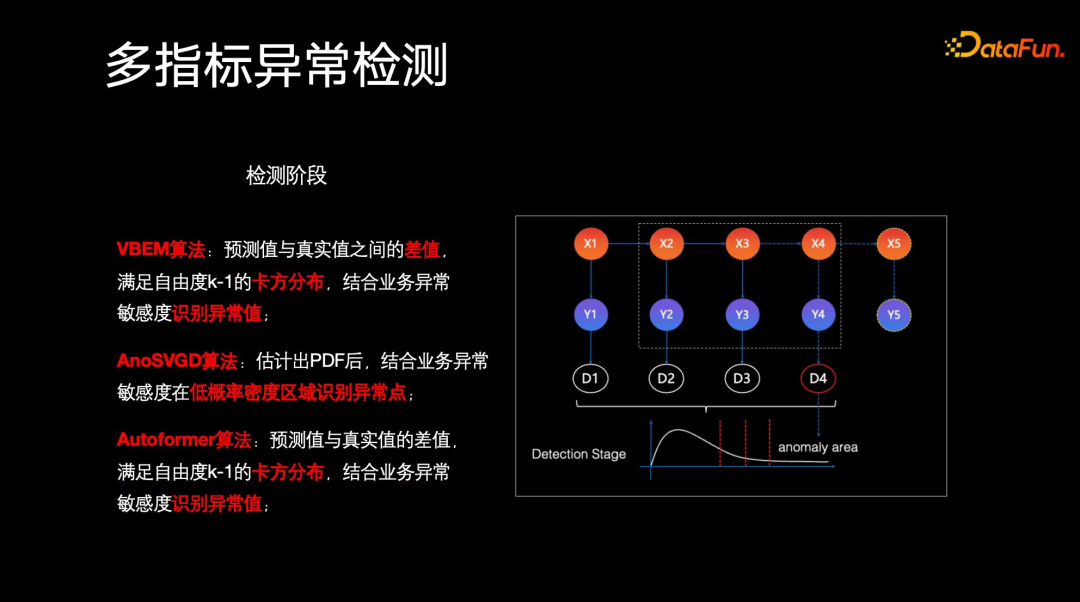
以上三种方法在完成训练之后,检测阶段分别需要处理的操作是:
- VBEM 算法,通过训练隐状态来生成下一个时刻的预测值,该预测值与真实值之间的差值满足自由度为 k-1 的卡方分布。结合业务配置的异常敏感度,我们可以识别出哪些点属于异常点,即是否落在异常区域内。这里的 k-1 的自由度相当于是服务器上不同监控指标的数量。
- AnoSVGD 算法,估计概率密度函数(PDF)后,结合业务敏感度来判断哪些值位于低概率密度区域,从而进行异常点识别。
- Autoformer 算法,与 VBEM 方法类似,也关注预测值和真实值之间的差异,满足自由度为 k-1 的卡方分布。在这个基础上结合业务敏感度来识别异常点。
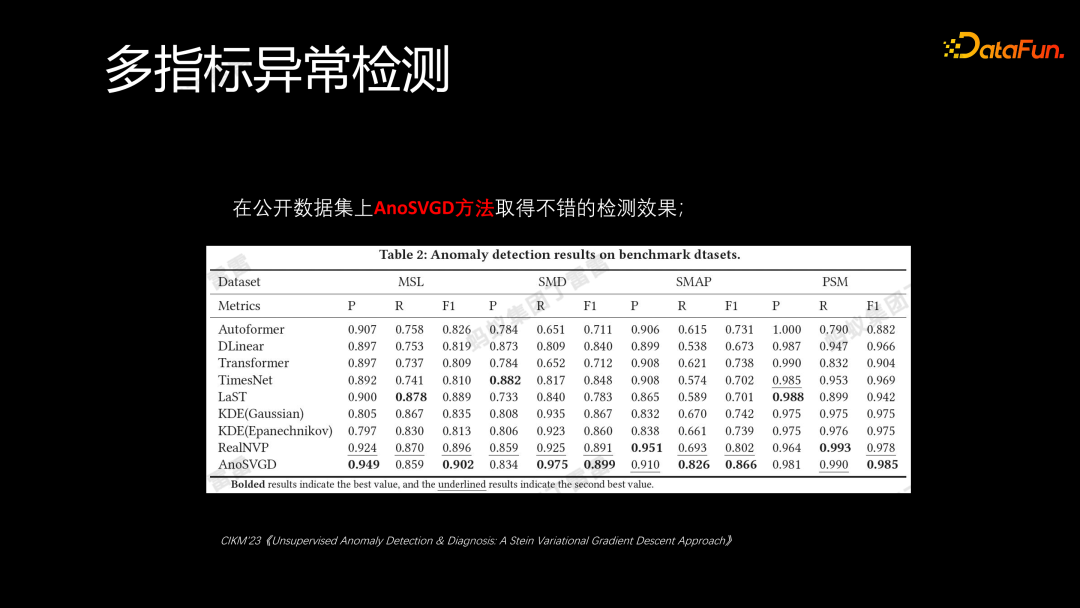
上述内容为我们在 CIKM 会议上发表的AnoSVGD 方法与其他方法例如 Autoformer、KDE 等方法在公开数据集上的对比结果,我们的 AnoSVGD 取得了非常出色的效果。
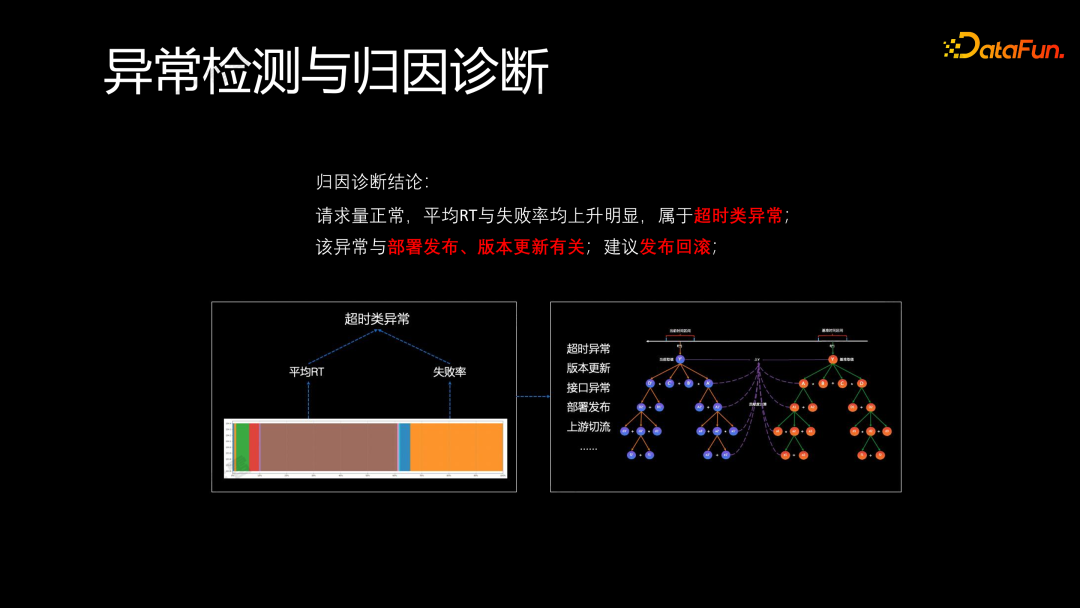
在多指标异常检测之后,仍然需要了解每个指标对当前异常的贡献度,这就要结合之前提到的归因诊断能力。例如,在一台机器上发生了多个指标的异常,发现平均响应时间(RT)和失败率是主要贡献异常的核心指标。通过归因诊断,就可以得出结论:在请求量正常的情况下,平均响应时间和失败率上升,明显属于超时类异常。这种异常一般与部署发布版本更新相关,因此建议 SRE(运维同学)执行发布回滚操作。
在实际应用中,我们已经实现了一些常规操作的自动执行,例如回滚操作。一旦检测到异常并关联到归因结论后,可以通过自动化手段自动回滚机器,恢复到正常状态。

整体的异常检测和归因诊断的过程总结如下:
- 模型训练、使用不同的算法模型进行训练。
- 最终进行模型预测,进行异常点检测。
- 获得检测结果后,计算其贡献度并进行归因诊断,找出导致异常的具体原因。
再次强调,当前我们的系统:
- 支持多敏感度调控
- 支持在线实时调优,用户可以实时反馈,在线实时进行调优
- 支持无监督增量指标的快速接入
- 支持多粒度的时间数据,目前主要以分钟级和小时级为主
- 支持实时归因诊断
- 支持秒级性能要求
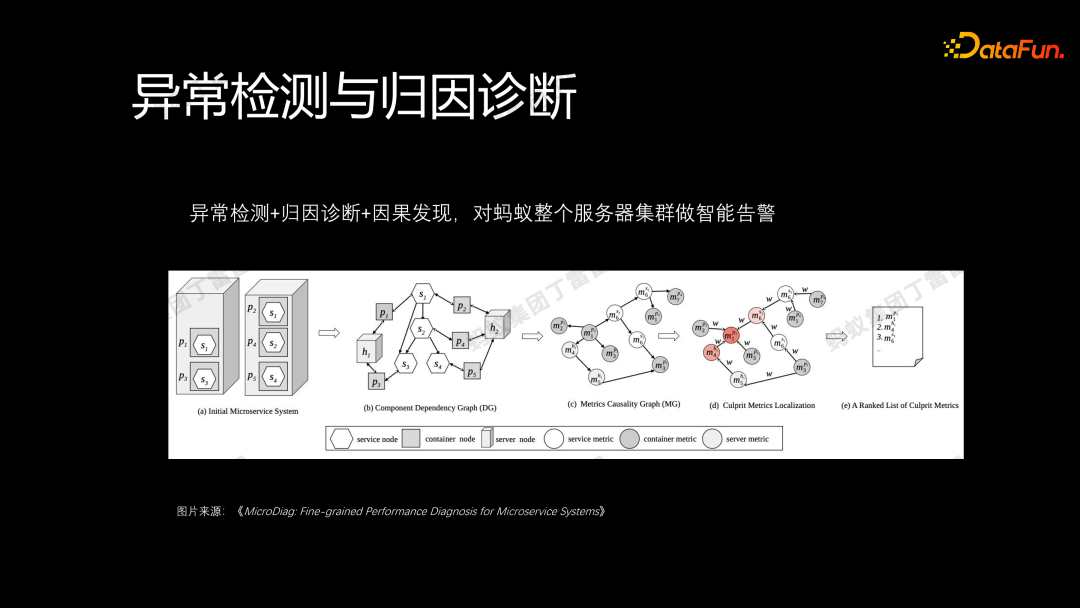
除了之前提到的内容,异常检测和归因诊断不仅可以应用于单个业务或机器的异常,还可以应用于整个集群。我们可以通过历史告警信息,挖掘告警之间的因果关系图,并结合服务调用图,当某台服务器发生告警时,就可以通过异常检测、归因诊断和因果发现来分析整个服务器集群链路,快速定位整个服务集群中的问题链路,确定核心原因和根因。
三、问题与挑战

最后,总结一下我们所面对的问题和挑战:
- 在归因诊断方面,存在辛普森悖论问题,即如何确保在对比时间区间内我们所对比的人群是同质的。如果人群不同质,那么我们得出的结论可能就失去了可信度。
- 在异常检测方面,在单指标异常检测中,可能会遇到频幅泄露问题,导致趋势周期的错误识别和不准确性。此外,无论是单指标还是多指标,都面临非平稳时序的问题。当时序的趋势和周期不断变化时,我们需要思考如何解决这一问题。