元老与新秀：Go sort.Search()和sort.Find()-51CTO.COM

sort.Search()

sort.Search() 提交于遥远的2010年11月11日,提交者是Go三位创始人之一的Robert Griesemer[1], 随Go第一个正式版本一起发布

从这个意义上说,是标准库元老级的函数了~

sort.Search()[2] 用于在排序的切片或数组中查找元素

// Search uses binary search to find and return the smallest index i
// in [0, n) at which f(i) is true, assuming that on the range [0, n),
// f(i) == true implies f(i+1) == true. That is, Search requires that
// f is false for some (possibly empty) prefix of the input range [0, n)
// and then true for the (possibly empty) remainder; Search returns
// the first true index. If there is no such index, Search returns n.
// (Note that the "not found" return value is not -1 as in, for instance,
// strings.Index.)
// Search calls f(i) only for i in the range [0, n).
//
// A common use of Search is to find the index i for a value x in
// a sorted, indexable data structure such as an array or slice.
// In this case, the argument f, typically a closure, captures the value
// to be searched for, and how the data structure is indexed and
// ordered.
//
// For instance, given a slice data sorted in ascending order,
// the call Search(len(data), func(i int) bool { return data[i] >= 23 })
// returns the smallest index i such that data[i] >= 23. If the caller
// wants to find whether 23 is in the slice, it must test data[i] == 23
// separately.
//
// Searching data sorted in descending order would use the <=
// operator instead of the >= operator.
//
// To complete the example above, the following code tries to find the value
// x in an integer slice data sorted in ascending order:
//
// x := 23
// i := sort.Search(len(data), func(i int) bool { return data[i] >= x })
// if i < len(data) && data[i] == x {
//  // x is present at data[i]
// } else {
//  // x is not present in data,
//  // but i is the index where it would be inserted.
// }
//
// As a more whimsical example, this program guesses your number:
//
// func GuessingGame() {
//  var s string
//  fmt.Printf("Pick an integer from 0 to 100.\n")
//  answer := sort.Search(100, func(i int) bool {
//   fmt.Printf("Is your number <= %d? ", i)
//   fmt.Scanf("%s", &s)
//   return s != "" && s[0] == 'y'
//  })
//  fmt.Printf("Your number is %d.\n", answer)
// }
func Search(n int, f func(int) bool) int {
 // Define f(-1) == false and f(n) == true.
 // Invariant: f(i-1) == false, f(j) == true.
 i, j := 0, n
 for i < j {
  h := int(uint(i+j) >> 1) // avoid overflow when computing h
  // i ≤ h < j
  if !f(h) {
   i = h + 1 // preserves f(i-1) == false
  } else {
   j = h // preserves f(j) == true
  }
 }
 // i == j, f(i-1) == false, and f(j) (= f(i)) == true  =>  answer is i.
 return i
}

这段代码是一个实现了二分查找算法的函数，名为 Search。这个函数用于在一个有序的范围内寻找满足特定条件的最小索引 i。以下是对这个函数的详细解释：

函数定义：Search(n int, f func(int) bool) int 定义了一个名为 Search 的函数，接收两个参数：一个整数 n 和一个函数 f。n 定义了搜索范围的大小（从 0 到 n，不包括 n），而 f 是一个接受整数输入并返回布尔值的函数。Search 函数返回一个整数，表示满足 f 条件的最小索引。
**条件函数 f**：f 函数定义了查找的条件。对于索引 i，如果 f(i) 为真，则对于所有 j > i，f(j) 也应为真。这意味着 f 在某点之前为假，之后变为真。Search 函数查找的是这个转变发生的点。
二分查找逻辑：

初始化两个指针 i 和 j，分别代表搜索范围的开始和结束。开始时，i 为 0，j 为 n。
在 i < j 的条件下循环执行。计算中点 h，并判断 f(h) 的值。
如果 f(h) 为假（false），则说明满足条件的索引在 h 的右侧，将 i 设置为 h + 1。
如果 f(h) 为真（true），则说明满足条件的索引可能是 h 或在 h 的左侧，将 j 设置为 h。
这个过程不断缩小搜索范围，直到找到转变点，即 f(i-1) 为假而 f(i) 为真的位置。

结果返回：当 i 与 j 相遇时，i 就是满足 f(i) 为真的最小索引。如果整个范围内没有找到满足条件的索引，则返回 n。

会在一个已排序的切片中进行二分查找(因此比线性搜索要快得多，尤其是在处理大型数据集时性能尤其明显), 最后返回一个索引，这个索引指向切片中第一个不小于指定值的元素。如果没有找到符合条件的元素，则返回的索引等于切片的长度。

使用时首先需要确保切片或数组已经是排序过的。其次需提供一个函数，这个函数定义了怎样判断切片中的元素是否满足自定义的查找条件。

如下,假设有一个整数切片，已经按升序排序，想找到第一个不小于某个给定值的元素的位置。

package main

import (
 "fmt"
 "sort"
)

func main() {
 // 已排序的切片
 numbers := []int{1, 2, 4, 6, 8, 10}

 // 要查找的值
 target := 5

 // 使用 sort.Search
 index := sort.Search(len(numbers), func(i int) bool {
  return numbers[i] >= target
 })

 // 输出结果
 if index < len(numbers) {
  fmt.Printf("找到了不小于 %d 的元素，索引为 %d，值为 %d\n", target, index, numbers[index])
 } else {
  fmt.Printf("没有找到不小于 %d 的元素，索引为 %d\n", target, index)
 }
}

在线运行[3]

输出:

找到了不小于 5 的元素，索引为 3，值为 6

上面代码中,sort.Search() 用于在 numbers 切片中查找第一个不小于 5 的元素。由于 4 后面的元素是 6，所以函数返回 6 的索引，即 3。

更多例子:

Go语言中sort.Search()的使用方法（数组中通过值来取索引）[4]

golang 中sort包sort.search()使用教程[5]

sort.Find()

而sort.Find() 则首次提交[6]于2022年3月30日, 随2022年8月2号发布的Go 1.19[7]一起发布

// Find uses binary search to find and return the smallest index i in [0, n)
// at which cmp(i) <= 0. If there is no such index i, Find returns i = n.
// The found result is true if i < n and cmp(i) == 0.
// Find calls cmp(i) only for i in the range [0, n).
//
// To permit binary search, Find requires that cmp(i) > 0 for a leading
// prefix of the range, cmp(i) == 0 in the middle, and cmp(i) < 0 for
// the final suffix of the range. (Each subrange could be empty.)
// The usual way to establish this condition is to interpret cmp(i)
// as a comparison of a desired target value t against entry i in an
// underlying indexed data structure x, returning <0, 0, and >0
// when t < x[i], t == x[i], and t > x[i], respectively.
//
// For example, to look for a particular string in a sorted, random-access
// list of strings:
//
// i, found := sort.Find(x.Len(), func(i int) int {
//     return strings.Compare(target, x.At(i))
// })
// if found {
//     fmt.Printf("found %s at entry %d\n", target, i)
// } else {
//     fmt.Printf("%s not found, would insert at %d", target, i)
// }
func Find(n int, cmp func(int) int) (i int, found bool) {
 // The invariants here are similar to the ones in Search.
 // Define cmp(-1) > 0 and cmp(n) <= 0
 // Invariant: cmp(i-1) > 0, cmp(j) <= 0
 i, j := 0, n
 for i < j {
  h := int(uint(i+j) >> 1) // avoid overflow when computing h
  // i ≤ h < j
  if cmp(h) > 0 {
   i = h + 1 // preserves cmp(i-1) > 0
  } else {
   j = h // preserves cmp(j) <= 0
  }
 }
 // i == j, cmp(i-1) > 0 and cmp(j) <= 0
 return i, i < n && cmp(i) == 0
}

这段代码是一个实现二分查找的算法函数，名为 Find。它的目的是在一个满足特定条件的有序集合中查找一个元素，并返回该元素的索引和一个布尔值，表示是否找到了该元素。以下是对该函数及其组成部分的详细解释：

函数定义：Find(n int, cmp func(int) int) (i int, found bool) 定义了一个名为 Find 的函数，它接受一个整数 n 和一个比较函数 cmp 作为参数。n 表示搜索范围的大小，而 cmp 是一个用于比较元素的函数。函数返回两个值：i（找到的元素的索引）和 found（一个布尔值，表示是否找到了元素）。
**比较函数 cmp**：这个函数接受一个整数索引作为输入，并返回一个整数。返回值的意义是基于目标值 t 与索引 i 处元素的比较：如果 t 小于元素，则返回小于 0 的值；如果 t 等于元素，则返回 0；如果 t 大于元素，则返回大于 0 的值。
二分查找逻辑：

初始化两个指针 i 和 j，分别指向搜索范围的开始和结束。i 初始化为 0，j 初始化为 n。
循环执行，直到 i 不小于 j。在每次迭代中，计算中点 h，并使用 cmp 函数比较中点处的元素。
如果 cmp(h) 的结果大于 0，说明目标值 t 在中点的右侧，因此将 i 更新为 h + 1。
如果 cmp(h) 的结果不大于 0，说明目标值 t 在中点或中点的左侧，因此将 j 更新为 h。
这个过程不断缩小搜索范围，直到 i 和 j 相遇。

结果返回：当循环结束时，i 和 j 相等。这时，如果 i 小于 n 且 cmp(i) 等于 0，则说明找到了目标元素，函数返回 i 和 found 为 true。否则，表示没有找到目标元素，函数返回 i（此时 i 表示目标值应该插入的位置，以保持序列的有序性）和 found 为 false。

Find uses binary search to find and return the smallest index i in [0, n) at which cmp(i) <= 0. If there is no such index i, Find returns i = n. The found result is true if i < n and cmp(i) == 0. Find calls cmp(i) only for i in the range [0, n).To permit binary search, Find requires that cmp(i) > 0 for a leading prefix of the range, cmp(i) == 0 in the middle, and cmp(i) < 0 for the final suffix of the range. (Each subrange could be empty.) The usual way to establish this condition is to interpret cmp(i) as a comparison of a desired target value t against entry i in an underlying indexed data structure x, returning <0, 0, and >0 when t < x[i], t == x[i], and t > x[i], respectively.

Find 使用二分查找来查找并返回 [0, n) 中 cmp(i) <= 0 的最小索引 i。如果不存在这样的索引 i，Find 将返回 i = n。如果 i < n 且 cmp(i) == 0，则找到的结果为 true。Find 仅针对 [0, n) 范围内的 i 调用 cmp(i)。

为了允许二分搜索，Find 要求 cmp(i) > 0 作为范围的前导前缀，cmp(i) == 0 在中间，cmp(i) < 0 作为范围的最后后缀。（每个子范围可以为空。）建立此条件的常用方法是将 cmp(i) 解释为所需目标值 t 与基础索引数据结构 x 中的条目 i 的比较，返回 <0、0 和 > 当 t < x[i]、t == x[i] 和 t > x[i] 时，分别为 0。

图片

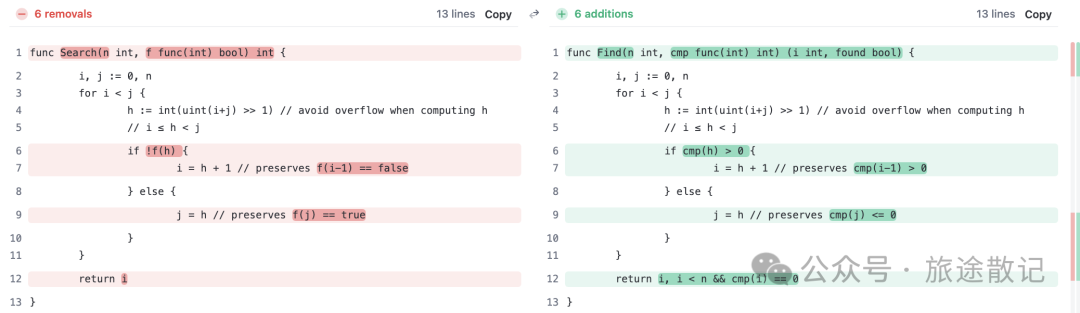
二者实现非常相近,都有用二分搜索

Find的第二个入参,也是一个func,但要求这个func的返回值是int而不是bool.另外Find的返回值有两个,第二个返回值是bool,代表没有找到指定元素

sort.Find()[8] 看起来和sort.Search()很像,为什么有了Search还需要Find?二者有什么不同?

回溯一下Find的历史, 提案sort: add Find #50340[9]是Go三位创始人之一的另一位Rob Pike[10]提出

从讨论中[11]:

It sounds like we agree that sort.Search is hard to use, but there's not an obvious replacement. In particular, anything that can report an exact position has to take a different function (a 3-way result like strings.Compare, or multiple functions).

"听起来我们都同意 sort.Search 很难使用，但没有明显的替代品。特别是，任何可以报告精确位置的东西都必须采用不同的函数（3 路结果，如 strings.Compare 或多个函数）"

slices: add Sort, SortStable, IsSorted, BinarySearch, and func variants #47619[12]

The difference between Search and Find in all cases would be that Find returns -1 when the element is not present,whereas Search returns the index in the slice where it would be inserted.

"在所有情况下，Search 和 Find 之间的区别在于，当元素不存在时，Find 返回 -1，而 Search 返回要插入元素的切片中的索引"

之所以Search大家感觉不够好用,是因为如果要查找的元素没在slice里面，Search会返回要插入元素的切片中的索引(并不一定是slice的长度,只有当元素比切片最后一个元素还大时,此时返回值才正好等于切片长度)，而绝对不是-1, 这样就没法判断某个元素是否在切片中, 可看下面的例子:

package main

import (
 "fmt"
 "sort"
)

func main() {

 data := []int{1, 2, 3, 5, 10}

 target0 := 4
 index0 := sort.Search(len(data), func(i int) bool {
  return data[i] >= target0
 })
 fmt.Println(index0) //3

 target1 := 5
 index1 := sort.Search(len(data), func(i int) bool {
  return data[i] >= target1
 })
 fmt.Println(index1) //3

 target2 := 6
 index2 := sort.Search(len(data), func(i int) bool {
  return data[i] >= target2
 })
 fmt.Println(index2) //4

 target3 := 11
 index3 := sort.Search(len(data), func(i int) bool {
  return data[i] >= target3
 })
 fmt.Println(index3) //5

}

正如Rob Pike所说,他想用sort.Search来做搜索,判断某个元素是否在(已排序的)切片中,但实际上,如target2的6, sort.Search()得到结果4, 是说如果把这个元素插入这个有序切片,需要插入在data[4]这个位置,并不一定是说data[4]=6

即通过sort.Search无法直接判断某个元素是否在切片中,还需要补一个 data[index]和target是否相等的判断

而Find则不然,

package main

import (
 "fmt"
 "sort"
 "strings"
)

func main() {

 x := []string{"a", "e", "h", "s", "v"}

 target := "e"
 i, found := sort.Find(len(x), func(i int) int {
  return strings.Compare(target, x[i])
 })
 if found {
  fmt.Printf("found %s at entry %d\n", target, i)
 } else {
  fmt.Printf("%s not found, would insert at %d\n", target, i)
 }

 target2 := "g"
 j, found2 := sort.Find(len(x), func(j int) int {
  return strings.Compare(target2, x[j])
 })
 if found2 {
  fmt.Printf("found %s at entry %d\n", target2, j)
 } else {
  fmt.Printf("%s not found, would insert at %d\n", target2, j)
 }

}

输出:

found e at entry 1
g not found, would insert at 2

即不光返回了应该插入到哪个位置,还把目标元素是否在切片中也返回了~

一定程度上,Find似乎放在slices包更合适:

https://github.com/golang/go/issues/50340#issuecomment-1034071670

https://github.com/golang/go/issues/50340#issuecomment-1034341823

我同意将 sort 和 slices 包的接口解耦。前者适用于抽象索引，而后者适用于实际切片

sort.Find 和 slices.BinarySearchFunc

其实,我觉得很大程度,是因为slices.Contains性能不够好(调用了slices.Index,即遍历检测), 而用sort.Find前提是一个已排序的切片,即可以用二分查找,肯定比用现在的slices.Contains暴力遍历要好

但其实,Contains不需要知道index,只需要知道在不在,有没有...可以考虑用map,虽然map的创建等需要一定的开销,但是对于元素数量非常多的case,hash查找的O(1)的优势就体现出来了~而且不需要切片的有序的

应该提一个提案,来优化现有的slices.Contains

Reference

[1]Robert Griesemer: https://github.com/griesemer

[2]sort.Search(): https://github.com/golang/go/blob/master/src/sort/search.go#L58

[3]在线运行: https://go.dev/play/p/6dlo5pwcNXy

[4]Go语言中sort.Search()的使用方法（数组中通过值来取索引）: https://blog.csdn.net/hty46565/article/details/109689515

[5]golang 中sort包sort.search()使用教程: https://studygolang.com/articles/14087

[6]首次提交: https://go-review.googlesource.com/c/go/+/396514

[7]2022年8月2号发布的Go 1.19: https://golang.google.cn/doc/devel/release

[8]sort.Find(): https://github.com/golang/go/blob/master/src/sort/search.go#L99

[9]sort: add Find #50340: https://github.com/golang/go/issues/50340

[10]Rob Pike: https://github.com/robpike

[11]讨论中: https://github.com/golang/go/issues/50340#issuecomment-1016736447

[12]slices: add Sort, SortStable, IsSorted, BinarySearch, and func variants #47619: https://github.com/golang/go/issues/47619#issuecomment-915428658