优化语义分割模型常用的损失有Soft Jaccard损失,Soft Dice损失和Soft Tversky损失,但它们都和软标签不兼容,所以无法支持一些重要的训练技术(例如标签平滑,知识蒸馏,半监督学习,多标注员等)。
另一方面,语义分割常用的评价指标有mAcc和mIoU,但是因为它们都会偏向数据集中尺寸较大的物体,所以会严重的影响它们对模型安全性能的评估。
为了解决这些问题,鲁汶大学和清华的研究人员首先提出了JDT损失。JDT损失是原有损失函数的变体,包括了Jaccard Metric损失,Dice Semimetric损失和Compatible Tversky损失。JDT损失在硬标签下与原有的损失函数等价,但能完全兼容软标签。
研究人员将JDT损失应用于软标签的四个重要场景:标签平滑、知识蒸馏、半监督学习和多标注员,展示了它们提高模型准确性和校准性的能力。
 图片
图片
论文链接:https://arxiv.org/pdf/2302.05666.pdf
 图片
图片
论文链接:https://arxiv.org/pdf/2303.16296.pdf
除此之外,研究人员还提出了细粒度的评价指标。这些细粒度的评价指标对大尺寸物体的偏见较小,能提供更丰富的统计信息,并能为模型和数据集审计提供有价值的见解。
并且,研究人员进行了一项广泛的基准研究,强调了不应基于单个指标进行评估的必要性,并发现了神经网络结构和JDT损失对优化细粒度指标的重要作用。
 图片
图片
论文链接:https://arxiv.org/pdf/2310.19252.pdf
代码链接:https://github.com/zifuwanggg/JDTLosses
现有的损失函数
由于Jaccard Index和Dice Score是定义在集合上的,所以并不可导。为了使它们可导,目前常见的做法有两种:一种是利用集合和相应向量的Lp模之间的关系,例如Soft Jaccard损失(SJL),Soft Dice损失(SDL)和Soft Tversky损失(STL)。
它们把集合的大小写成相应向量的L1模,把两个集合的交集写成两个相应向量的内积。另一种则是利用Jaccard Index的submodular性质,在集合函数上做Lovasz拓展,例如Lovasz-Softmax损失(LSL)。
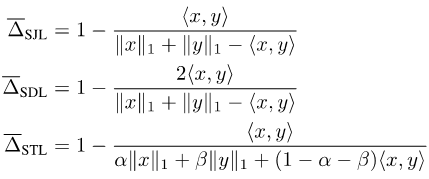 图片
图片
这些损失函数都假定神经网络的输出x是一个连续的向量,而标签y则是一个离散的二值向量。如果标签为软标签,即y不再是一个离散的二值向量,而是一个连续向量时,这些损失函数就不再兼容。
以SJL为例,考虑一个简单的单像素情况:
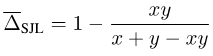 图片
图片
可以发现,对于任意的y > 0,SJL都将在x = 1时最小化,而在x = 0时最大化。因为一个损失函数应该在x = y时最小化,所以这显然是不合理的。
与软标签兼容的损失函数
为了使原有的损失函数与软标签兼容,需要在计算两个集合的交集和并集时,引入两个集合的对称差:
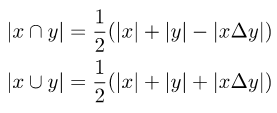 图片
图片
注意两个集合的对称差可以写成两个相应向量的差的L1模:
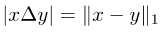 图片
图片
把以上综合起来,我们提出了JDT损失。它们分别是SJL的变体Jaccard Metric损失(JML),SDL的变体Dice Semimetric 损失(DML)以及STL的变体Compatible Tversky损失(CTL)。
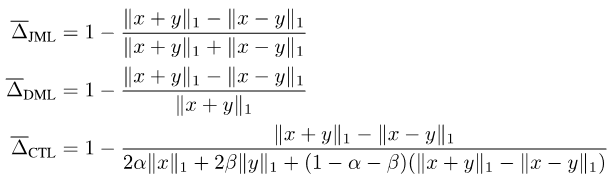 图片
图片
JDT损失的性质
我们证明了JDT损失有着以下的一些性质。
性质1:JML是一个metric,DML是一个semimetric。
性质2:当y为硬标签时,JML与SJL等价,DML与SDL等价,CTL与STL等价。
性质3:当y为软标签时,JML,DML,CTL都与软标签兼容,即x = y ó f(x,y) = 0。
由于性质1,它们也因此被称为Jaccard Metric损失和Dice Semimetric损失。性质2说明在仅用硬标签进行训练的一般场景下,JDT损失可以直接用来替代现有的损失函数,而不会引起任何的改变。
如何使用JDT损失
我们进行了大量的实验,总结出了使用JDT损失的一些注意事项。
注意1:根据评价指标选择相应的损失函数。如果评价指标是Jaccard Index,那么应该选择JML;如果评价指标是Dice Score,那么应该选择DML;如果想给予假阳性和假阴性不同的权重,那么应该选择CTL。其次,在优化细粒度的评价指标时,JDT损失也应做相应的更改。
注意2:结合JDT损失和像素级的损失函数(例如Cross Entropy损失,Focal损失)。本文发现0.25CE + 0.75JDT一般是一个不错的选择。
注意3:最好采用一个较短的epoch来训练。加上JDT损失后,一般只需要Cross Entropy损失训练时一半的epoch。
注意4:在多个GPU上进行分布式训练时,如果GPU之间没有额外的通信,JDT损失会错误的优化细粒度的评价指标,从而导致其在传统的mIoU上效果变差。
注意5:在极端的类别不平衡的数据集上进行训练时,需注意JDL损失是在每个类别上分别求损失再取平均,这可能会使训练变得不稳定。
实验结果
实验证明,与Cross Entropy损失的基准相比,在用硬标签训练时,加上JDT损失可以有效提高模型的准确性。引入软标签后,可以进一步提高模型的准确性和校准性。
 图片
图片
只需在训练时加入JDT损失项,本文取得了语义分割上的知识蒸馏,半监督学习和多标注员的SOTA。
 图片
图片
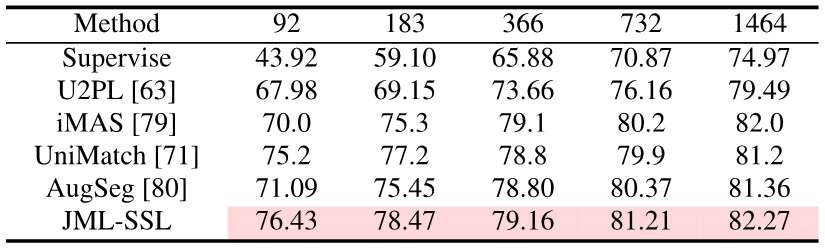 图片
图片
 图片
图片
现有的评价指标
语义分割是一个像素级别的分类任务,因此可以计算每个像素的准确率:overall pixel-wise accuracy(Acc)。但因为Acc会偏向于多数类,所以PASCAL VOC 2007采用了分别计算每个类别的像素准确率再取平均的评价指标:mean pixel-wise accuracy(mAcc)。
但由于mAcc不会考虑假阳性,从PASCAL VOC 2008之后,就一直采用平均交并比(per-dataset mIoU, mIoUD)来作为评价指标。PASCAL VOC是最早的引入了语义分割任务的数据集,它使用的评价指标也因此被之后的各个数据集所广泛采用。
具体来说,IoU可以写成:
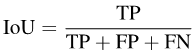 图片
图片
为了计算mIoUD,我们首先需要对每一个类别c统计其在整个数据集上所有I张照片的true positive(真阳性,TP),false positive(假阳性,FP)和false negative(假阴性,FN):
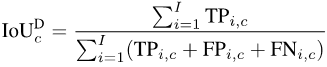 图片
图片
有了每个类别的数值之后,我们按类别取平均,从而消除对多数类的偏好:
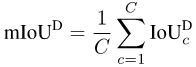 图片
图片
因为mIoUD把整个数据集上所有像素的TP,FP和FN合计在一起,它会不可避免的偏向于那些大尺寸的物体。
在一些对安全要求较高的应用场景中,例如自动驾驶和医疗图像,经常会存在一些尺寸小但是不可忽略的物体。
如下图所示,不同照片上的汽车的大小有着明显的不同。因此,mIoUD对大尺寸物体的偏好会严重的影响其对模型安全性能的评估。

细粒度的评价指标
为了解决mIoUD的问题,我们提出细粒度的评价指标。这些指标在每张照片上分别计算IoU,从而能有效的降低对大尺寸物体的偏好。
mIoUI
对每一个类别c,我们在每一张照片i上分别计算一个IoU:
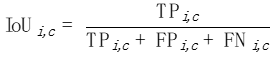 图片
图片
接着,对每一张照片i,我们把这张照片上出现过的所有类别进行平均:
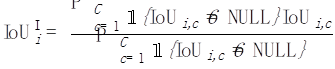 图片
图片
最后,我们把所有照片的数值再进行平均:
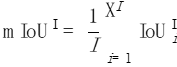 图片
图片
mIoUC
类似的,在计算出每个类别c在每一张照片i上的IoU之后,我们可以把每一个类别c出现过的所有照片进行平均:
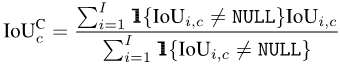
最后,把所有类别的数值再进行平均:
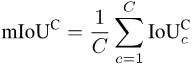
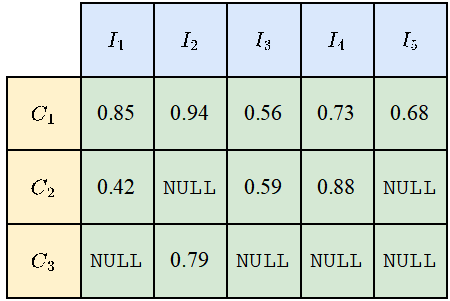
由于不是所有的类别都会出现在所有的照片上,所以对于一些类别和照片的组合,会出现NULL值,如下图所示。计算mIoUI时先对类别取平均再对照片取平均,而计算mIoUC时先对照片取平均再对类别取平均。
这样的结果是mIoUI可能会偏向那些出现得很频繁的类别(例如下图的C1),而这一般是不好的。但另一方面,在计算mIoUI时,因为每张照片都有一个IoU数值,这能帮助我们对模型和数据集进行一些审计和分析。
 图片
图片
最差情况的评价指标
对于一些很注重安全的应用场景,我们很多时候更关心的是最差情况的分割质量,而细粒度指标的一个好处就是能计算相应的最差情况指标。我们以mIoUC为例,类似的方法也可以计算mIoUI相应的最差情况指标。
对于每一个类别c,我们首先把其出现过的所有照片(假设有Ic个这样的照片)的IoU数值进行升序排序。接着,我们设q为一个很小的数字,例如1或者5。然后,我们仅用排序好的前Ic * q%张照片来计算最后的数值:
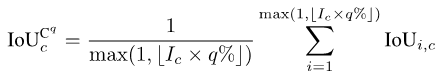 图片
图片
有了每个类c的数值之后,我们可以像之前那样按类别取平均,从而得到mIoUC的最差情况指标。
实验结果
我们在12个数据集上训练了15个模型,发现了如下的一些现象。
现象1:没有一个模型在所有的评价指标上都能取得最好的效果。每个评价指标都有着不同的侧重点,因此我们需要同时考虑多个评价指标来进行综合的评估。
现象2:一些数据集上存在部分照片使得几乎所有的模型都取得一个很低的IoU数值。这一方面是因为这些照片本身就很有挑战性,例如一些很小的物体和强烈的明暗对比,另一方面也是因为这些照片的标签存在问题。因此,细粒度的评价指标能帮助我们进行模型审计(发现模型会犯错的场景)和数据集审计(发现错误的标签)。
现象3:神经网络的结构对优化细粒度的评价指标有着至关重要的作用。一方面,由ASPP(被DeepLabV3和DeepLabV3+采用)等结构所带来的感受野的提升能帮助模型识别出大尺寸的物体,从而能有效提高mIoUD的数值;另一方面,encoder和decoder之间的长连接(被UNet和DeepLabV3+采用)能使模型识别出小尺寸的物体,从而提高细粒度评价指标的数值。
现象4:最差情况指标的数值远远低于相应的平均指标的数值。下表展示了DeepLabV3-ResNet101在多个数据集上的mIoUC和相应的最差情况指标的数值。一个值得以后考虑的问题是,我们应该如何设计神经网络结构和优化方法来提高模型在最差情况指标下的表现?
 图片
图片
现象5:损失函数对优化细粒度的评价指标有着至关重要的作用。与Cross Entropy损失的基准相比,如下表的(0,0,0)所示,当评价指标变得细粒度,使用相应的损失函数能极大的提升模型在细粒度评价指标上的性能。例如,在ADE20K上,JML和Cross Entropy损失的mIoUC的差别会大于7%。
 图片
图片
未来工作
我们只考虑了JDT损失作为语义分割上的损失函数,但它们也可以应用在其他的任务上,例如传统的分类任务。
其次,JDT损失只被用在标签空间中,但我们认为它们能被用于最小化任意两个向量在特征空间上的距离,例如用来替代Lp模和cosine距离。
参考资料:
https://arxiv.org/pdf/2302.05666.pdf
https://arxiv.org/pdf/2303.16296.pdf
https://arxiv.org/pdf/2310.19252.pdf
































