排序是一种组织数据的方式，目的是确保数据元素之间的相对顺序正确。当我们提到比较排序，意味着我们通过两两比较来确定元素之间的顺序。
理论上，一个最优的比较排序算法应该在每次比较后尽量减少剩余的可能性。
为了理解这点，考虑一个 N 个元素的所有 N! 种排列方式。在最优的方法中，每次比较都能使剩下的可能性减半，从 N!/2，N!/4，N!/8，...，N!/（2^k），……，1。
所以，对于 N 个元素的序列，为了确定一个特定的排列，最下限的情况下，我们需要进行 log(N!) 次比较。这是因为当 2^k = N! 时，k = log(N!)。
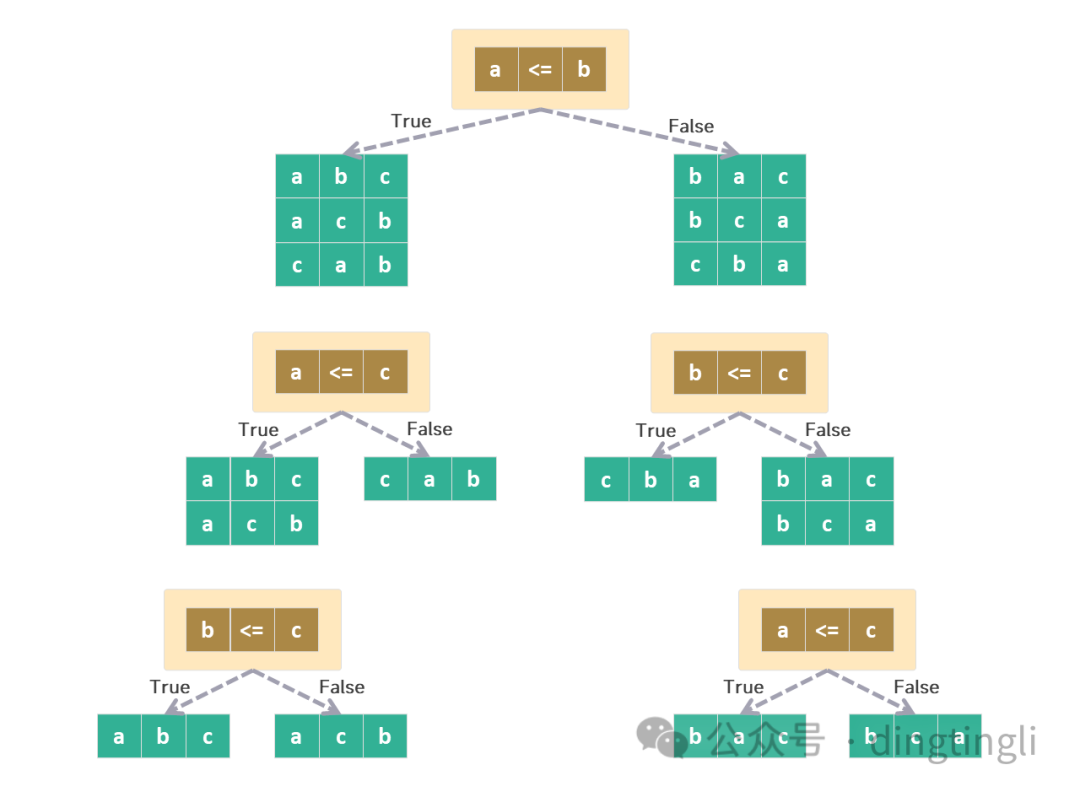
三个元素 a，b，c 序列的排序
但为什么现有的排序算法还不能达到这种理想状态呢？
为什么堆排序（HEAPSORT）不够快
首先，让我们回顾一下堆排序的实现：
- 建立最大堆： 将任意数组转化为最大堆。
- 找到最大元素并交换： 最大的元素始终位于数组的第一个位置，将数组的第一个元素与最后一个元素交换。
- 重建最大堆： 排除最后一个元素，并在剩余的元素中重新构建最大堆。
- 重复上述过程： 继续交换、排除和重建。
详情可以阅读之前的文章：堆排序的原理与实现。
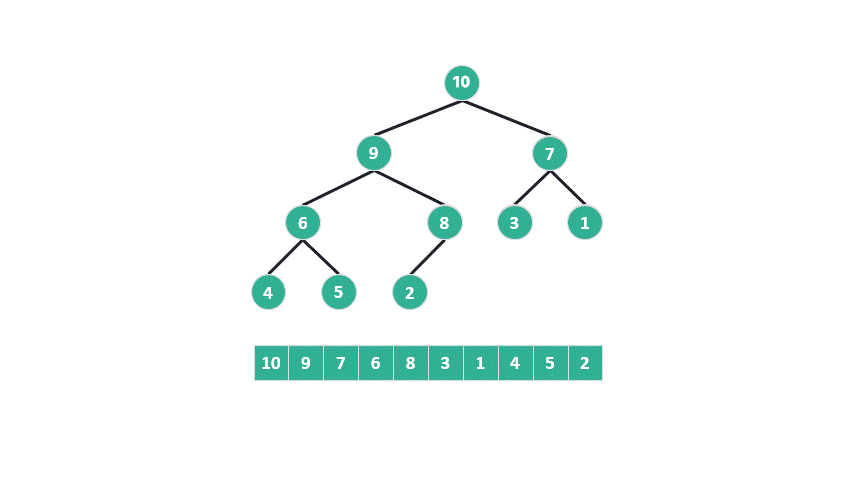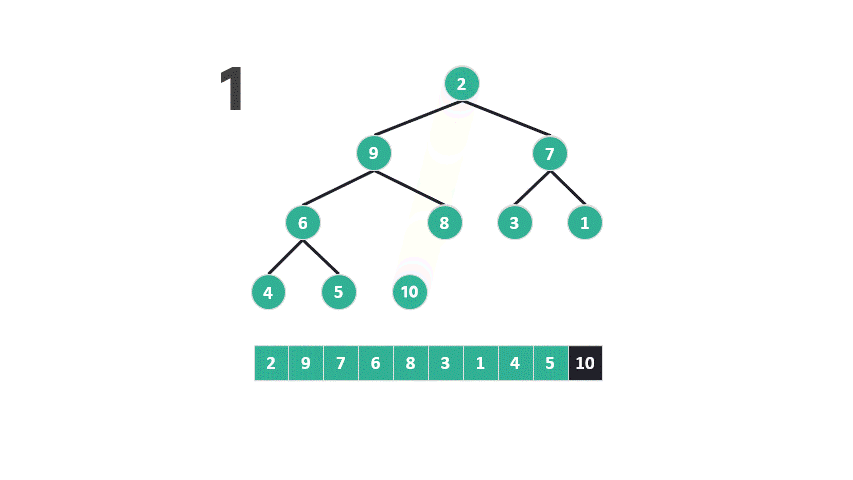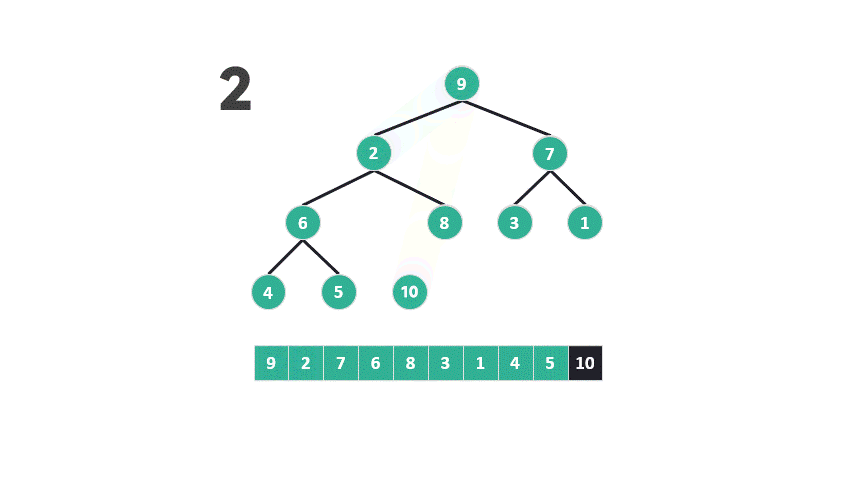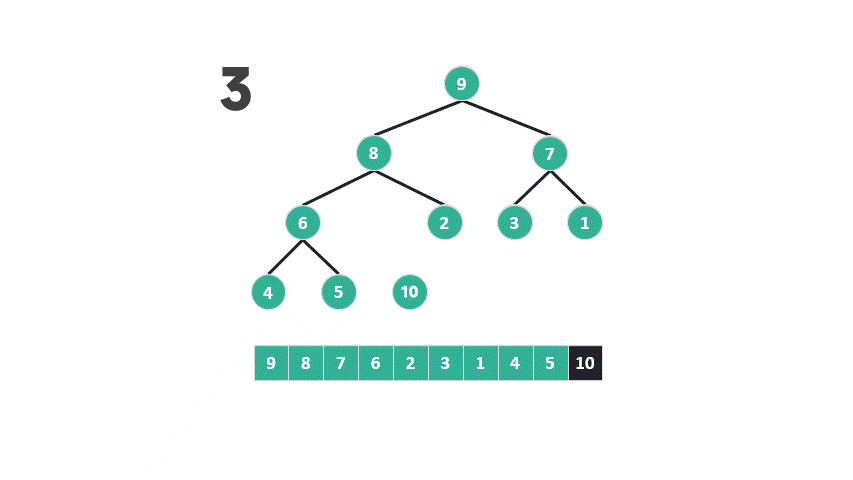
问题出在第二步，根据最大堆的定义，底部元素较小。堆排序将较小的元素从堆的底部提升到顶部，然后再让它们逐渐下沉，与较大的元素交换位置。
动图 重建最大堆示意图
你可以在我的 github 仓库中查看堆排序源代码：
https://github.com/dingtingli/algorithm/blob/main/Code/heapsort01.py
这种操作在堆排序中似乎违反了直觉：为什么要将底部可能较小的元素提升到更高的位置，然后观察其下沉的过程？
当底部元素被提升为父节点时，它几乎总是小于其中一个子节点，而大于另一个子节点的机会相对较少。因此，重建最大堆时进行的比较具有不均等的概率。这种概率不均等的比较是低效的，因为它不能保证每次比较都能将可能性减半。
这种操作效率的问题是堆排序速度较慢的主要原因。
然而，我们可以尝试以下优化方法：
优化方法的思想，就好比一个公司的老板离职需要被组织中最优秀的人替代，我们显然需要比较两位副总裁；问题是，我们是否期望这将是一场势均力敌的竞争？
在没有先验信息的情况下，我们没有充分的理由押注任何一位副总裁。情况中只有一种不对称性：这两个部门的总人数可能不等。副总裁"A"可能是比"副总裁"B"稍多的人中的佼佼者；一个大部门的最优秀者更有可能击败一个小部门的最优秀者。
优化后的 HEAPSORT：
- 将所有元素放入有效的最大堆中
- 删除堆顶，创建一个空缺 "V"
- 比较 V 正下方的两个子堆首领，将最大的那个提升到空缺中。
- 递归重复第 3 步，重新定义 V 为新的空缺，直到堆的底部。
- 转到步骤 2
你可以在我的 github 仓库中查看快速堆排序源代码：
https://github.com/dingtingli/algorithm/blob/main/Code/heapsort03.py
这种方法的优势在于，我们实际上是将一个已知较大的元素提升至堆顶，无需额外的比较操作。此时，两种比较结果的概率是均等的。我们将这种优化版本称为 "快速堆排序"（FAST HEAPSORT）。
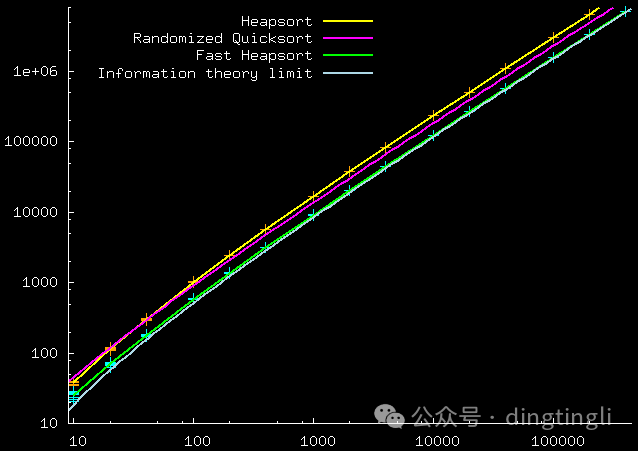
经过优化后的 "快速堆排序"很有可能是最接近理论极限的排序算法。
快速堆排序
横坐标：要排序的项目数 N。纵坐标：二分比较次数。
理论曲线显示了快速堆排序的渐近结果（2NlnN）和极限 log_2 N! 近似。
为什么快速排序（QUICKSORT）不够快
快速排序的核心分为两个过程：
- 选择数组中的一个元素为支点（pivot），将小于等于支点的元素移到左侧，将大于支点的元素移动到右侧。这一步称为划分（partition）。
- 通过递归对左右两侧的子数组继续划分，直到数组排序完成。
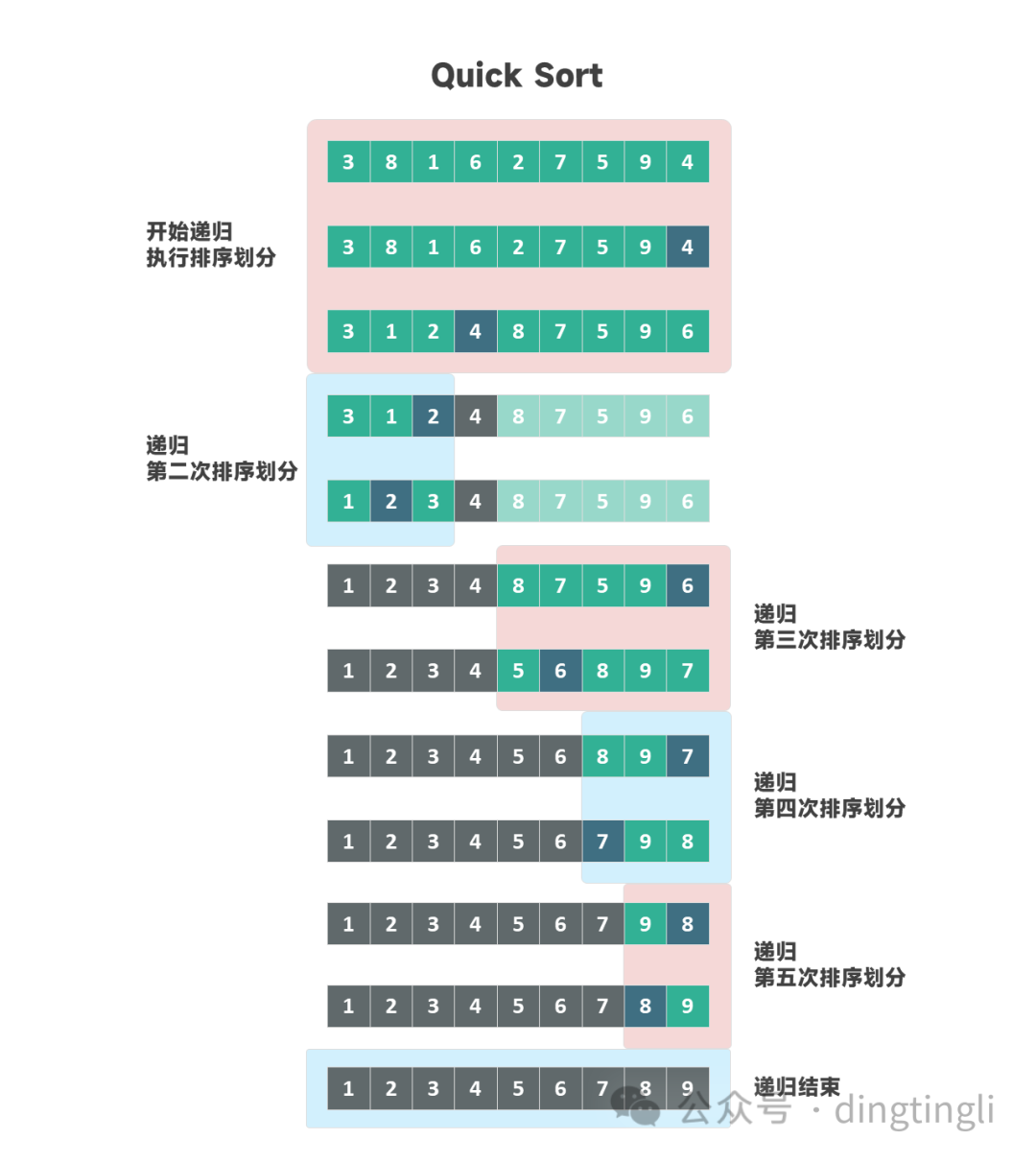划分递归执行
详情可以阅读之前的文章：快速排序的原理与实现。
为了进一步说明，假设有一个由三个元素组成的序列：pivot, a1 和 a2。
在快速排序的划分阶段，首先，我们会将 a1 与 pivot 进行比较。显然，(a1 < pivot) 和 (a1 > pivot) 可能性各占一半，这使得第一次比较达到了理想的效果。
然而，第二次的比较并不像第一次那样完美。
假设第一次比较已经确定 (a1 < pivot) ，此时我们需要进一步判断 a2 与 pivot 之间的关系。
考虑所有的组合可能性：基于 a1、a2 和 pivot 的相对顺序，总共存在 3! 即 6 种可能的排列：
- (a1 < a2 < pivot)
- (a1 < pivot < a2)
- (a2 < a1 < pivot)
- (a2 < pivot < a1)
- (pivot < a1 < a2)
- (pivot < a2 < a1)
由于已知 (a1 < pivot)，第 4、第 5 和第 6 种情况可以直接排除，这使得我们只考虑：
- (a1 < a2 < pivot)
- (a1 < pivot < a2)
- (a2 < a1 < pivot)
在这三种情况中，(a2 < pivot) 的可能性有 2 种，而 (a2 > pivot) 的情况仅有 1 种。
所以 (a2 < pivot) 的概率是 2/3，而 (a2 > pivot) 的概率是 1/3。
这就是快排也不那么快的原因，因为它并不总能确保每次比较都将可能性减半。
为什么基数排序（RADIXSORT）很快
基数排序之所以高效，是因为它脱离了传统比较排序的框架，不再通过两两元素的比较来决定排序顺序。
想象一下这样一个任务：整理一副扑克牌中同一花色的牌。假设手中有 N（N≤13）张牌，要如何迅速地给它们排好序呢？可以想象桌上已经预留出了 13 个特定的位置，每张牌会根据其点数被精准地放在对应位置。
比如，2 点的牌会放在第二个位置，而 Q 则被放置在第 12 个位置。所有牌放好后，按照位置顺序收集，你就得到了有序的扑克牌。
这个例子揭示了基数排序的核心效率。每张新牌的放置位置实际上是在前 i 张牌所定义的 i+1 个区间中选择的。
例如，如果我们已经放置了 2,5,8 这三张牌，那么我们就有四个区间来放置下一张牌：2 之前、2 和 5 之间、 5 和 8 之间，以及 8 之后。
当你放置第 i+1 张牌时，你实际上是在这些 i+1 个区间中选择一个位置放置它。一旦选择了一个区间放置新牌，其他的 i 个区间都被排除了。
因此，每放置一张新牌，你都减少了大约 i/i+1 的排序可能性。而基于比较的排序方法，每次操作最多只能减少排序可能性的一半。
比较排序的本质就像我们之前介绍的二分法游戏，然而除了二分法，我们还介绍了三分法游戏。基数排序更进一步，本质就像是 N 分法。
看图聊算法：一个游戏让你理解二分法的本质
看图聊算法：还是一个游戏，让你理解三分法的本质
这就是基数排序之所以高效的原因，它摆脱了比较的排序算法复杂度上限只能是 O(NlogN) 的命运。
然而，基数排序有其局限性。比如需要知道数据的范围或宽度，而且主要适用于整数和字符串。对于浮点数和复数，基数排序也不太合适。
结论
在算法中，我们通常使用大O记号来描述复杂度。但这种表示并非完美无缺。当我们使用"O"符号强调“对于大N的渐进性能”，这似乎暗示我们对 O(4NlogN) 和 O(1NlogN) 两种算法之间的差异不甚关心。
然而，这种常数因子的差异仍然是众多研究者追求和努力的焦点。即使排序算法的时间复杂度已达到理论上的界限 O(NlogN)，其演进仍在继续。
参考资料：
[1] http://www.inference.org.uk/mackay/sorting/sorting.html
[2] http://mindhacks.cn/2008/06/13/why-is-quicksort-so-quick
