在本系列的 上一篇文章中，我们学习了使用 Anaconda，加强了概率论的知识。在本文中我们将继续学习概率论的知识，学习使用 seaborn 和 Pandas 进行数据可视化，并进一步介绍 TensorFlow 和 Keras 的使用。
让我们从增长人工智能和机器学习的理论知识开始。众所周知人工智能、机器学习、数据科学、深度学习等是当今计算机科学的热门话题。然而，计算机科学还其他热门的话题，比如 区块链blockchain、物联网Internet of Things（IoT）、量子计算quantum computing等。那么，人工智能领域的发展是否会对这些技术产生积极的影响呢？
首先，让我们讨论一下区块链。根据维基百科的定义，“区块链是一种分布式账本，它由不断增长的记录（称为 区块block）组成，这些记录使用加密技术安全地连接在一起。”乍一看，人工智能和区块链似乎是两个高速发展的独立技术。但令人惊讶的是，事实并非如此。区块链相关的行话是 完整性integrity，人工智能相关的行话是数据。我们将大量数据交给人工智能程序去处理。虽然这些应用程序产生了惊人的结果，但我们如何信任它们呢？这就提出了对可解释的人工智能的需求。它可以提供一定的保证，以便最终用户可以信任人工智能程序提供的结果。许多专家认为，区块链技术可以用来提高人工智能软件做出的决策的可信度。另一方面，智能合约smart contract（区块链技术的一部分）可以从人工智能的验证中受益。从本质上讲，智能合约和人工智能通常都是做决策。因此，人工智能的进步将对区块链技术产生积极影响，反之亦然。
下面让我们讨论一下人工智能和物联网之间的影响。早期的物联网设备通常没有强大的处理能力或备用电池。这使得需要大量处理能力的机器学习的软件无法部署在物联网设备上。当时，大多数物联网设备中只部署了基于规则的人工智能软件。基于规则的人工智能的优势在于它很简单，需要相对较少的处理能力。如今的物联网设备具备更强大的处理能力，可以运行更强大的机器学习软件。特斯拉开发的高级驾驶辅助系统 特斯拉自动驾驶仪Tesla Autopilo
最后，让我们讨论人工智能和量子计算是如何相互影响的。尽管量子计算仍处于起步阶段，但 量子机器学习quantum machine learning（QML）是其中非常重要的课题。量子机器学习基于两个概念：量子数据和量子-经典混合模型。量子数据是由量子计算机产生的数据。量子神经网络quantum neural network（QNN）用于模拟量子计算模型。TensorFlow Quantum 是一个用于量子-经典混合机器学习的强大工具。这类工具的存在表明，在不久的将来将会有越来越多的基于量子计算的人工智能解决方案。
seaborn 入门
seaborn 是一个基于 Matplotlib 的数据可视化 Python 库。用它能够绘制美观且信息丰富的统计图形。通过
Anaconda Navigator 可以轻松安装 seaborn。我用 ESPNcricinfo 网站上 T20
国际板球赛的击球记录，创建了一个名为 T20.csv 的 CSV（逗号分隔值comma-separated value）文件，其中包含以下
15
列：球员姓名、职业生涯跨度、比赛场次、局数、未出局次数、总得分、最高得分、平均得分、面对球数、击球率、百分次数、五十分次数、零分次数、四分次数和六分次数。图
1 是使用 Pandas 库读取这个 CSV 文件的程序代码。我们已经在前面介绍过 Pandas 了。
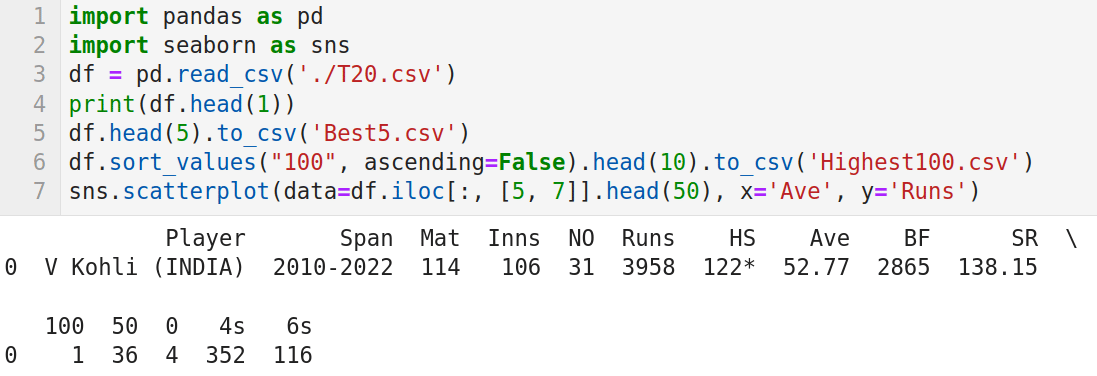图 1：使用 seaborn 的简单例子
下面逐行解释程序代码的作用。第 1 行和第 2 行导入 Pandas 和 seaborn 包。第 3 行从 JupyterLab 的工作目录中读取文件 T20.csv。第 4 行打印元数据和第一行数据。图 1 显示了这行数据，它显示了 T20 国际板球赛中得分最高的 Virat Kohli 的击球记录。第 5 行将元数据和 T20.csv 中的前五行数据保存到 Best5.csv 中。在执行该行代码时会在 JupyterLab 的工作目录中创建这个文件。第 6 行根据列百分次数按升序对 CSV 文件进行排序，并将前 10 名世纪得分手的详细信息存储到 Highest100.csv 中。该文件也将存储在 JupyterLab 的工作目录中。最后，第7行代码提取了第 5 列（总得分）和第 7 列（平均得分）的数据信息，并生成散点图。图 2 显示了程序在执行时生成的散点图。
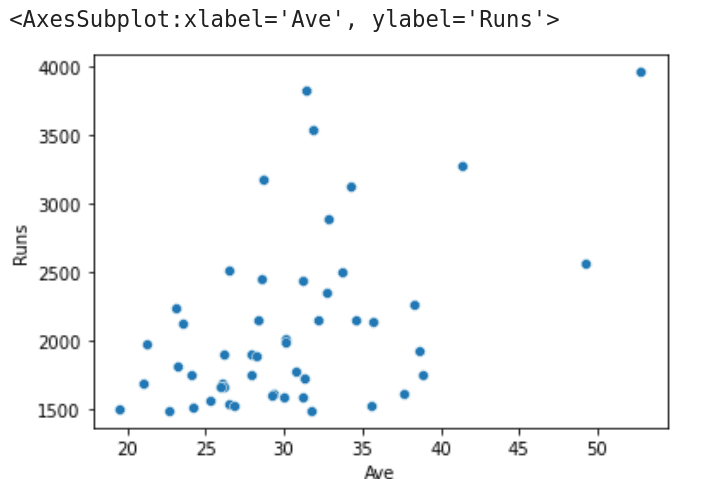图 2：seaborn 绘制的散点图
在程序末尾添加如下代码行并再次运行。
sns.kdeplot(data=df.iloc[:, [5, 7]].head(50), x=’Ave’, y=’Runs’)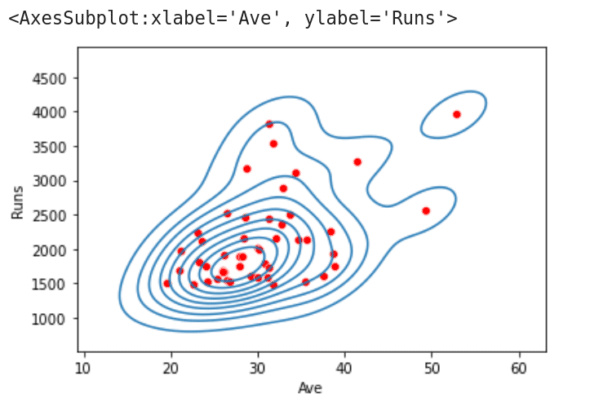
图 3：使用 seaborn 绘制的核密度估计图
这行代码调用 kdeplot() 函数绘制第 5 列和第 7 列数据的 核密度估计Kernel Distribution Estimation（KDE）图。KDE 图可以描述连续或非参数数据变量的概率密度函数。这个定义可能无法让您了解函数 kdeploy() 将要执行的实际操作。图 3 是在单个图像上绘制的 KDE 图和散点图。从图中我们可以看到，散点图绘制的数据点被 KDE 图分组成簇。seaborn 还提供了许多其他绘图功能。在图 1 中程序的第 7 行分别替换为下面的的代码行（一次一行），并再次执行该程序，你会看到不同风格的绘图显示。探索 seaborn 提供的其他绘图功能，并选择最适合你需求的功能。
sns.histplot(data=df.iloc[:, [5, 7]].head(50), x=’Ave’, y=’Runs’)
sns.rugplot(data=df.iloc[:, [5, 7]].head(50), x=’Ave’, y=’Runs’)更多概率论
在本系列之前的一篇文章中，我们看到可以用正态分布来对现实场景进行建模。但正态分布只是众多重要概率分布中的一种。图 4 中的程序绘制了三种概率分布。
图 4：绘制多种概率分布的程序
下面我来解释这个程序。第 1 行导入 NumPy 的 random 模块。第 2 行和第 3 行导入用于绘图的 Matplotlib 和 seaborn。第 5 行生成带有参数 n（试验次数）和 p（成功概率）的 二项分布binomial distribution数据。
二项分布是一种离散概率分布，它给出了在一系列 n 次独立实验中成功的数量。第三个参数 size 决定了输出的形状。第 6 行绘制生成的数据的直方图。由于参数 kde=True，它还会绘制 KDE 图。第三个参数 color='r' 表示绘图时使用红色。第 7 行生成一个泊松分布。泊松分布是一种离散概率分布，它给出了二项分布的极限。参数 lam 表示在固定时间间隔内发生预期事件的次数。这里的参数 size 也决定了输出的形状。第 8 行将生成的数据绘制为绿色的直方图。第 9 行生成大小为 1000 的指数分布。第 10 行将生成的数据绘制为蓝色的直方图。最后，第 11 绘制三个概率分布的所有图像（见图 5）。NumPy 的 random 模块提供了大量的其他概率分布，如 Dirichlet 分布、Gamma 分布、几何分布、拉普拉斯分布等。学习和熟悉它们将是非常值得的。
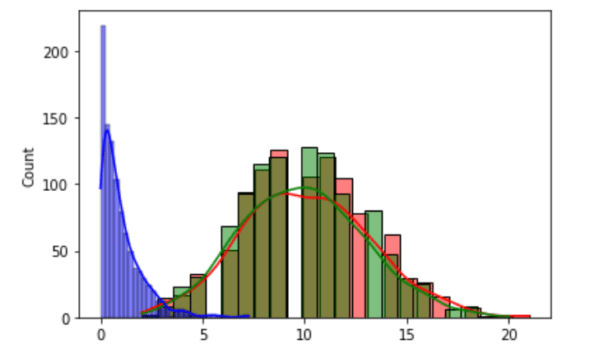图 5：概率分布的图像
现在，让我们学习线性回归。使用线性回归分析可以根据一个变量来预测一个变量的值。线性回归的一个重要应用是数据拟合。线性回归非常重要，因为它很简单。机器学习中的监督学习范式实际上就是回归建模。因此，线性回归可以被认为是一种重要的机器学习策略。这种学习范式通常被统计学家称为统计学习。线性回归是机器学习中的重要操作。NumPy 和 SciPy 都提供了线性回归的函数。下面我们展示使用 NumPy 和 SciPy 进行线性回归的示例。
图 6：使用 NumPy 进行线性回归
图 6 是使用 NumPy 进行线性回归的程序。第 1 行和第 2 行导入 NumPy 和 Matplotlib。第 4 行和第 5 行初始化变量 a和 b。第 6 行使用函数 linspace() 在 0 和 1 之间等间隔地生成 100 个数字。第 7 行使用变量 a、b 和数组 x 生成数组 y 中的值。函数 randn() 返回标准正态分布的数据。第 8 行将数组 x 和 y 中的值绘制成散点图（见图 7），图中的 100 个数据点用红色标记。第 9 行使用函数 polyfit() 执行称为 最小二乘多项式拟合least squares polynomial fit 的线性回归技术。函数 polyfit() 的输入参数包括数组 x 和 y，以及第三个表示拟合多项式的阶数的参数，在本例中为 1，表示拟合一条直线。该函数的返回值是多项式的系数，代码中将其存储在数组 p 中。第 10 行使用函数 polyval() 对多项式求值，并将这些值存储在数组y_l中。第 11 行用蓝色绘制拟合得到的直线（见图 7）。最后，第 12 行显示所有的图像。可以用这条回归直线预测可能的 (x, y) 数据对。
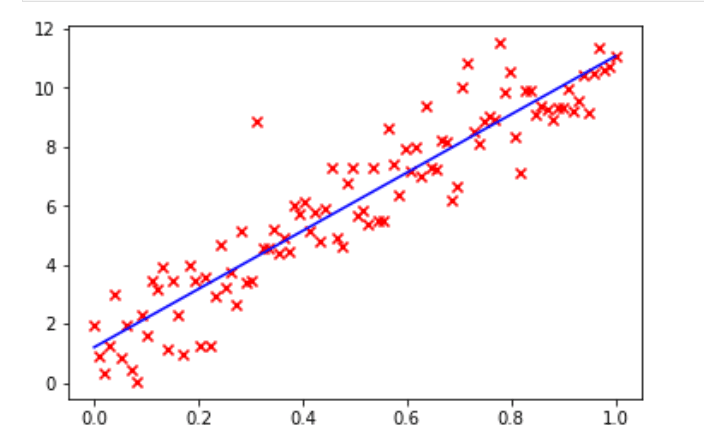图 7：线性回归散点图 1
图 8 是使用 SciPy 进行线性回归的程序代码。
图 8：使用 SciPy 进行线性回归
下面我解释一下这个程序的工作原理。第 1 行和第 2 行导入库 NumPy 和 Matplotlib。第 3 行从库 SciPy 导入 stats 模块。第 4 到 8 行与前面的程序执行类似的任务。第 9 行使用 SciPy 的 stats 模块的 linregression() 函数计算两组测量值的线性最小二乘回归——在本例中是数组 x 和 y 中的值。该函数返回值中的 m 和 c 分别表示回归直线的 斜率slope和截距intercept。第 10 行使用斜率和截距的值生成回归线。第 11 行用绿色绘制回归线。最后，第 12 行显示所有的图像（见图 9），其中数据点以黄色显示，回归线以绿色显示。
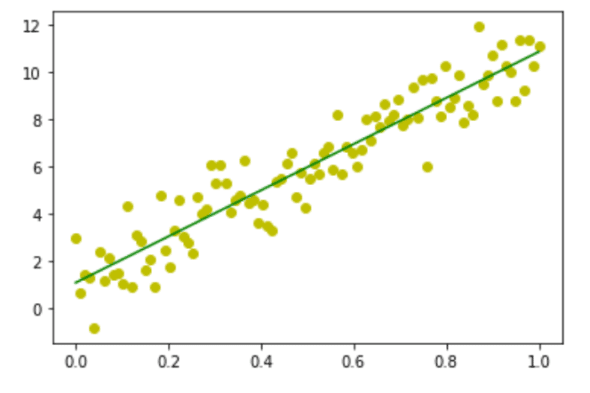图 9：线性回归散点图 2
在本系列的前面几篇文章中，我们学习了概率和统计学的一些概念。尽管还不够全面的，但我认为这已经打下了一个良好的基础，现在是时候将注意力转移到其他同样重要的问题上了。
Keras 简介
Keras 一般与 TensorFlow 一起使用。因此，我们先从使用 TensorFlow 开始。图 10 所示的程序虽然只包含四行代码，但确实构建了在本系列中的第一个神经网络。下面我来介绍它的工作原理。第 1 行导入库 TensorFlow。第 2 行创建了一个名为 x 的张量。第 3 行和第 4 行分别在张量 x 上应用 ReLU（整流线性单元Rectified Linear Unit）和 Leaky ReLU 激活函数。在神经网络中，激活函数定义了节点的输出由输入计算出的规则。ReLU 激活函数是定义为 Relu(x) = max(0,x)。第 3 行代码的输出如图 10 所示。可以观察到，在应用 ReLU 激活函数后，张量 x 中的负值被替换为零。Leaky ReLU 是 ReLU 激活函数的改进版本。从图 10 中的第 4 行代码的输出可以看出 Leaky ReLU 激活函数保留了全量的正值和 20% 的负值。在后面我们将会继续讨论 Keras，同时学习更多神经网络和激活函数的知识。
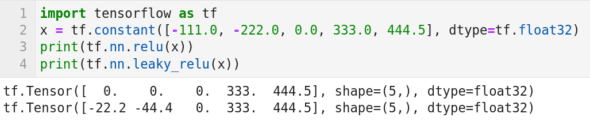图 10：使用 TensorFlow 实现的神经网络
下面我们开始使用 Keras。Keras 的安装也可以通过 Anaconda Navigator 轻松完成。图 11 所示的程序导入了我们的第一个数据集并显示了其中的一个数据样本。在下一篇文章中，我们将使用这个数据集来训练和测试模型，从而开启我们开发人工智能和机器学习程序的下一个阶段。
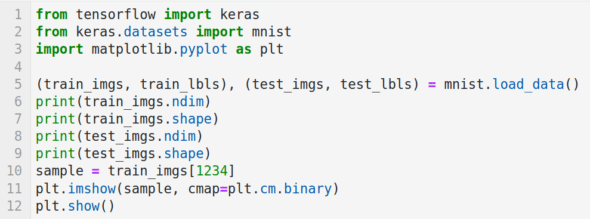图 11：第一个数据集
下面介绍这个程序的工作原理。第 1 行导入 Keras。第 2 行从 Keras 导入手写数字数据集 MNIST。它包含 6 万个训练样本和 1 万个测试样本。第 3 行导入 Matplotlib。第 5 行加载 MNIST 数据集。第 6 到 9 行打印训练集和测试集的维数和维度。图 12 显示了这些代码行的输出。可以看出，训练集和测试集都是三维的，所有数据样本的分辨率都是 28 × 28。第 10 行加载了第 1234 个训练图像。第 11 行和第 12 行显示这个图像。从图 12 可以看到它是数字 3 的手写图像。
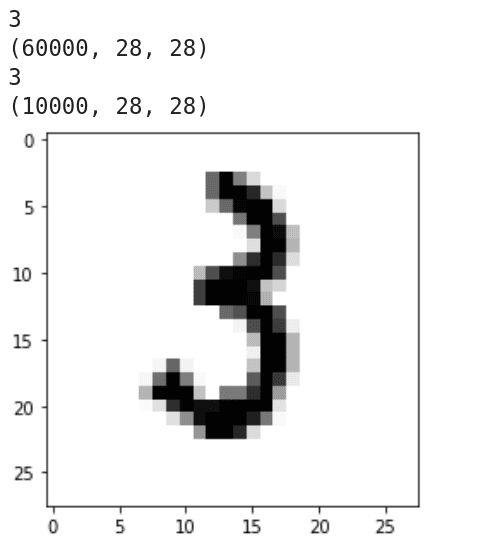图 12：数据样例
本文中我们开始涉及到神经网络，并通过 Keras 接触到了第一个数据集。在下一篇文章中，我们将继续讲解神经网络和 Keras，并通过使用该数据集训练自己的模型。我们还会遇到 scikit-learn, 它是另一个强大的机器学习 Python 库 。
