人工智能数学基础 - 线性代数之矩阵篇-51CTO.COM

本文将从矩阵的本质、矩阵的原理、矩阵的应用三个方面，带您一文搞懂人工智能数学基础-线性代数之矩阵。

一、矩阵的本质

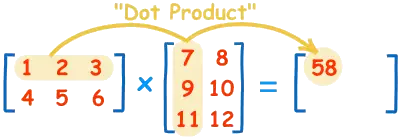
点积（Dot Product）：点积作为向量间的一种基本运算，通过对应元素相乘后求和来刻画两向量的相似度和方向关系。

点积（Dot Product）

一、定义

点积，又称为数量积或标量积，是两个同维度向量之间的一种运算。对于两个n维向量A和B，点积是将它们的对应元素相乘后求和得到的结果。

二、符号表示

点积通常使用符号"·"或"<A, B>"来表示。即，若A和B是两个向量，则它们的点积可以表示为A·B或<A, B>。

三、计算方法

确保向量A和B的维度相同，即它们都有n个元素。
将向量A和B的对应元素相乘，得到n个乘积。
将这n个乘积相加，得到最终的点积结果。

数学公式表示为：A·B = a1b1 + a2b2 + ... + an*bn，其中ai和bi分别是向量A和B的第i个元素。

矩阵（Matrix）：矩阵是数值的矩形阵列，通过特定的运算规则（如矩阵乘法），在数学、科学及工程领域中实现数据变换和问题解决的关键工具。

矩阵（Matrix）

一、定义

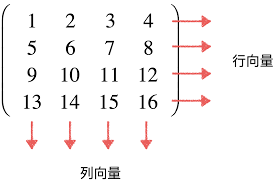
矩阵是一个数值的矩形阵列，它在数学、物理学、工程学和计算机科学等多个领域中都有广泛应用。矩阵由行和列组成，每个元素在矩阵中都有确定的位置。

二、符号表示

矩阵通常用大写的粗体字母表示，例如A、B、C等。矩阵的尺寸由其行数和列数决定，一个m×n的矩阵表示它有m行和n列。

矩阵中的每个数值被称为元素。元素的位置由其所在的行和列决定，通常用下标表示。例如，在矩阵A中，第i行第j列的元素可以表示为A[i][j]。

三、矩阵乘法

矩阵乘法是一种特殊的运算，不同于常规的元素间乘法。对于两个矩阵A和B，只有当A的列数等于B的行数时，它们才能进行矩阵乘法。结果矩阵C的尺寸是A的行数乘以B的列数。

矩阵乘法的计算遵循以下步骤：

验证矩阵A的列数是否等于矩阵B的行数。如果不相等，则无法进行矩阵乘法。
创建一个新的矩阵C，其行数与矩阵A相同，列数与矩阵B相同。
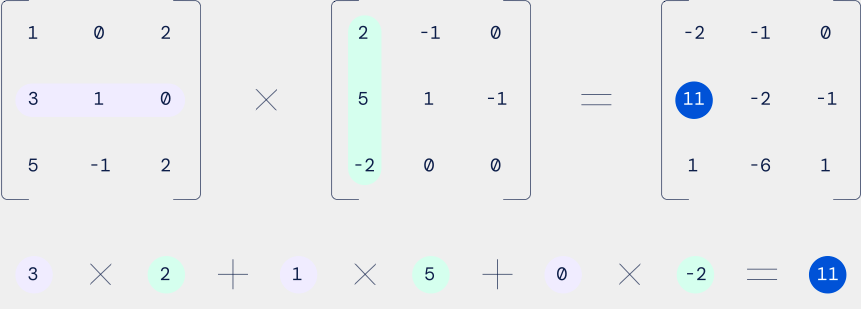
对于矩阵C中的每个元素C[i][j]，计算它是矩阵A的第i行与矩阵B的第j列的对应元素乘积之和。即，C[i][j] = A[i][k1] * B[k1][j] + A[i][k2] * B[k2][j] + ... + A[i][kn] * B[kn][j]，其中k1, k2, ..., kn是矩阵A的列索引或矩阵B的行索引。

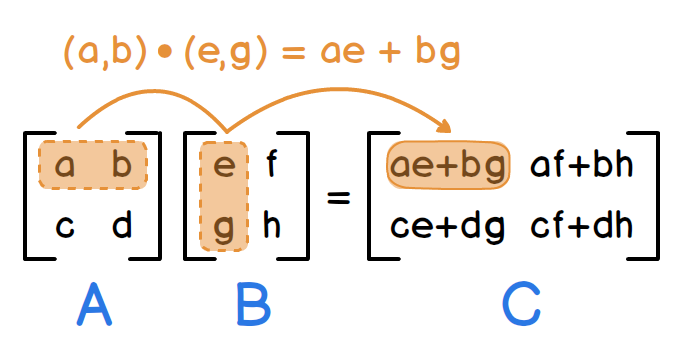矩阵乘法

二、矩阵的原理

线性方程组求解：将N元一次方程组转化为矩阵运算，可以简化求解过程，提高计算效率，并在多个领域中得到广泛应用。

齐次线性方程组

一、线性方程组的基本概念

定义：线性方程组是由一组线性方程（即未知数的次数均为1的方程）构成的集合。每个方程可以表示为ax + by + ... + z = c的形式，其中a, b, ...是常数，x, y, ..., z是未知数。
表示：线性方程组通常可以用矩阵形式来表示。具体地，我们可以将方程组的系数提取出来形成一个系数矩阵，将常数项组成一个常数向量，从而将原方程组转化为矩阵方程。

二、线性方程组的矩阵表示

系数矩阵：对于线性方程组中的每个方程，将其未知数前的系数提取出来，按照方程的顺序排列成一个矩阵，称为系数矩阵（记为A）。
常数向量：将线性方程组中的常数项（即等号右边的数值）按照方程的顺序排列成一个列向量，称为常数向量（记为b）。
未知数向量：定义一个列向量，其元素个数与线性方程组中的未知数个数相同，用于表示未知数的解，称为未知数向量（记为x）。
矩阵方程：将系数矩阵、常数向量和未知数向量结合起来，形成矩阵方程Ax = b，其中A是系数矩阵，x是未知数向量，b是常数向量。

三、线性方程组的求解方法

高斯消元法：

通过一系列行变换（交换行、倍加行、倍减行），将系数矩阵变换为上三角矩阵或对角矩阵。
从最后一行开始，逐步回代求解未知数。

矩阵的逆：

如果系数矩阵A是可逆的（即存在逆矩阵A^(-1)），则可以通过计算逆矩阵直接求解未知数向量，即x = A^(-1)b。
注意：不是所有矩阵都有逆矩阵，只有满秩矩阵（行列式不为0）才可逆。

克拉默法则：

利用行列式的性质，通过计算系数矩阵的行列式和伴随矩阵来求解线性方程组。
克拉默法则适用于任何规模的线性方程组，但计算量随着未知数个数的增加而急剧增加。

主成分分析（PCA）：主成分分析（PCA）是一种统计方法，用于简化数据集并揭示其内在结构。

主成分分析（PCA）

1.标准化数据集

在开始PCA之前，通常会对原始数据集进行标准化处理。标准化后的数据集将具有零均值和单位方差，这对于后续的计算和分析是重要的。

输出：标准化后的数据集矩阵。

2. 协方差矩阵

标准化数据集之后，计算其协方差矩阵。协方差矩阵捕获了数据集中各特征之间的关系和变化的幅度。

输出：协方差矩阵。

3. 特征值和特征向量

通过对协方差矩阵进行特征值分解，PCA得到一组特征值和对应的特征向量。特征值的大小反映了对应特征向量方向上数据变化的重要性。

输出：

特征值列表（按降序排列）。
对应的特征向量矩阵，其中每一列是一个特征向量。

4. 主成分

根据特征值的大小，选择前k个最大的特征值对应的特征向量作为主成分。这些主成分构成了一个新的低维空间，用于表示原始数据。

输出：主成分矩阵，其中每一列是一个主成分（即选定的特征向量）。

5. 投影数据

将原始数据投影到主成分构成的低维空间上，得到降维后的数据表示。

输出：投影后的数据集矩阵，其维度低于原始数据集。

三、矩阵的应用

马尔可夫矩阵：马尔可夫矩阵描述了系统中状态之间的转移概率，是马尔可夫链模型的核心，广泛应用于预测、决策、模式识别和强化学习等领域。

def print_markov_matrix(matrix, state_labels):  
    """  
    结构化输出马尔可夫矩阵，并附带状态标签。


    :param matrix: 马尔可夫矩阵  
    :param state_labels: 状态标签列表  
    """  
    num_states = len(matrix)  
    print(f"马尔可夫状态转移矩阵（{num_states}个状态）:")  
    print("    " + "   ".join(state_labels))  # 打印状态标签头部  
    for i in range(num_states):  
        row_data = [f"{matrix[i][j]:.2f}" for j in range(num_states)]  
        print(f"{state_labels[i]}: {'   '.join(row_data)}")  
  
# 示例：天气预测模型的状态转移矩阵  
states = ['晴天', '多云', '雨天']  
transition_matrix = [  
    [0.8, 0.15, 0.05],  # 晴天转移到其他天气的概率  
    [0.2, 0.7, 0.1],    # 多云转移到其他天气的概率  
    [0.1, 0.3, 0.6]     # 雨天转移到其他天气的概率  
]  
  
print_markov_matrix(transition_matrix, states)

状态转移矩阵：

当前状态\下一状态	晴天	多云	雨天
晴天	0.8	0.15	0.05
多云	0.2	0.7	0.1
雨天	0.1	0.3	0.6

说明：

此矩阵描述了一个天气预测模型中的状态转移概率。
模型中有三个状态：晴天、多云、雨天。
矩阵中的每个元素表示从当前状态转移到下一状态的概率。
例如，第一行表示如果今天是晴天，那么明天仍然是晴天的概率为0.8，变为多云的概率为0.15，变为雨天的概率为0.05。

在AI中的应用：

预测：使用此马尔可夫矩阵，我们可以预测未来几天的天气情况。通过连续应用状态转移概率，我们可以估计出从当前天气状态出发，未来几天内各个天气状态出现的可能性。
决策支持：在农业、旅游、交通等领域，基于天气预测的马尔可夫模型可以为相关决策提供数据支持。例如，农民可以根据预测的天气情况来决定是否播种或收割；旅游公司可以根据天气趋势来制定旅游路线和计划。
强化学习：在马尔可夫决策过程中，状态转移矩阵是环境模型的一部分，智能体（Agent）通过学习这些转移概率来制定最优策略，以最大化累积奖励。

卷积和池化操作：卷积通过滤波器提取局部特征，池化则减少数据维度并保留关键信息，二者在深度学习中共同促进图像、文本和音频等数据的高效处理与特征学习。

概念说明：

卷积：在深度学习和计算机视觉中，卷积是一种数学运算，用于提取图像或信号中的局部特征。它通过应用一个滤波器（或卷积核）在输入数据上滑动并进行逐元素乘法运算来实现。
池化：池化（Pooling）是一种下采样技术，用于减少数据的空间维度（高度和宽度），同时保留重要信息。它通过在输入数据的不同区域上应用一个聚合函数（如最大值、平均值等）来实现。

卷积操作

输入：图像（或其他类型数据）的局部区域与卷积核进行对应元素相乘。
输出：卷积后的特征图，反映了输入数据中与卷积核相似的特征。
应用：在图像处理中，卷积可以用于边缘检测、模糊、锐化等任务；在深度学习中，卷积神经网络（CNN）使用卷积层来自动学习图像中的有用特征。

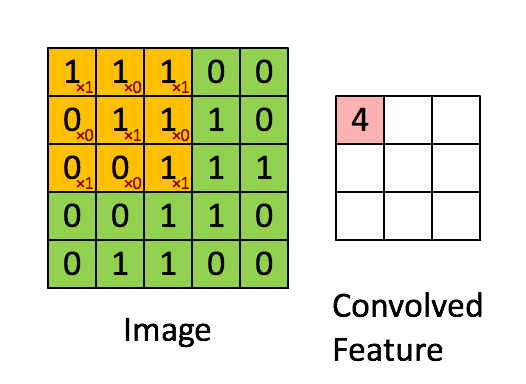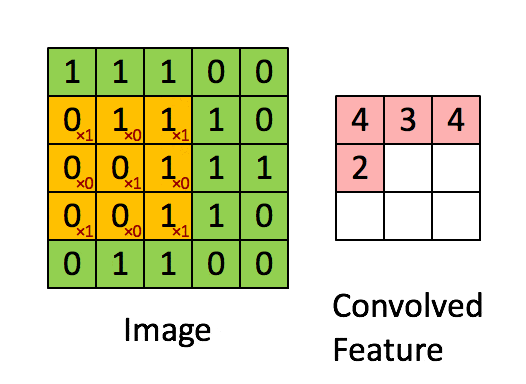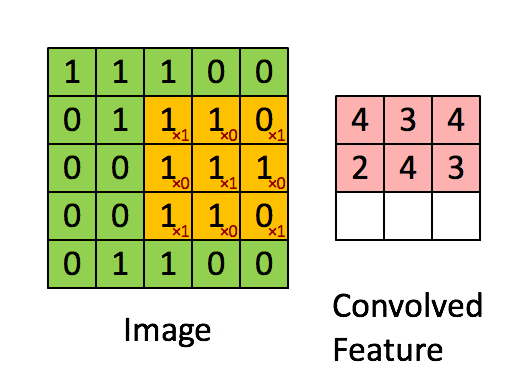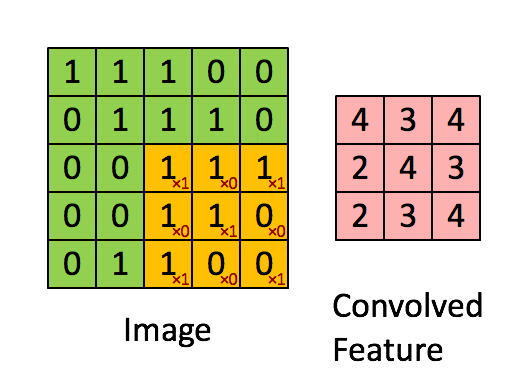卷积操作

池化操作

输入：卷积后的特征图。
输出：下采样后的特征图，空间维度减小，但保留了重要信息。
应用：池化层通常位于卷积层之后，用于减少计算量、内存使用和过拟合风险，同时提高模型的泛化能力。

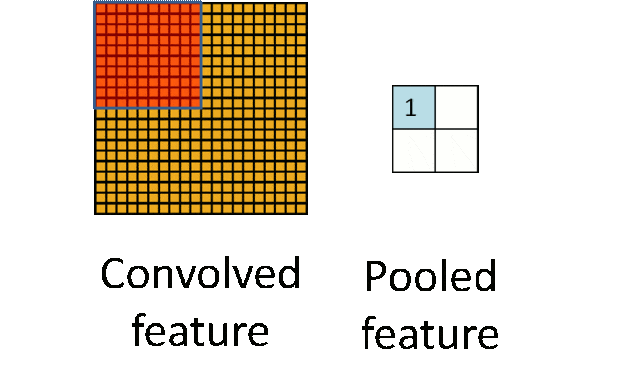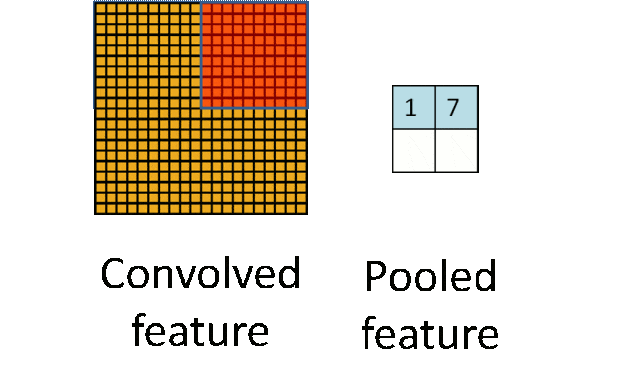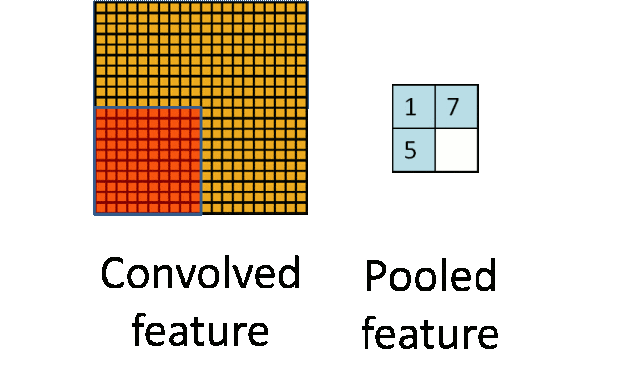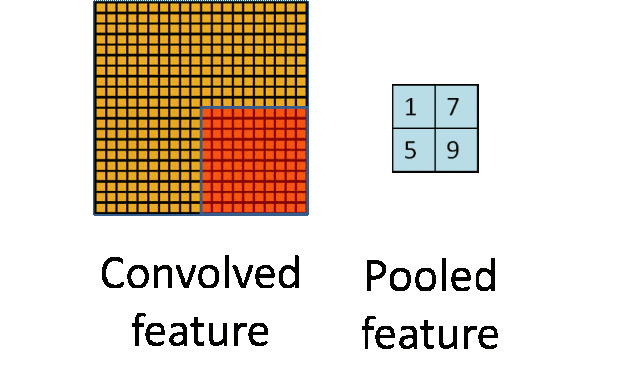池化操作

在AI中的应用：

图像识别：卷积神经网络（CNN）是图像识别任务中最常用的模型之一。它们通过交替使用卷积层和池化层来自动学习图像中的层次化特征表示，从而实现高效的图像分类、目标检测等任务。
自然语言处理：尽管卷积和池化最初是为图像处理设计的，但它们也被成功应用于自然语言处理任务中。例如，卷积操作可以用于提取文本中的n-gram特征或进行句子级别的分类任务；池化操作则可用于对变长文本序列进行下采样，以便输入到固定大小的模型中。
语音识别：在语音识别领域，卷积和池化操作可以用于提取音频信号的局部特征，如时频表示（如梅尔频率倒谱系数MFCC）或直接从原始波形中学习特征。这些特征可以进一步用于构建语音识别系统或音频分类模型。