使用Pytorch构建图卷积网络预测化学分子性质-51CTO.COM

在本文中，我们将通过化学的视角探索图卷积网络，我们将尝试将网络的特征与自然科学中的传统模型进行比较，并思考为什么它的工作效果要比传统的方法好。

图和图神经网络

化学或物理中的模型通常是一个连续函数，例如y=f(x₁，x₂，x₃，…，x)，其中x₁，x₂，x₃，…，x是输入，y是输出。这种模型的一个例子是确定两个点电荷q 1和q 2之间的静电相互作用(或力)的方程，它们之间的距离r存在于具有相对介电常数εᵣ的介质中，通常称为库仑定律。

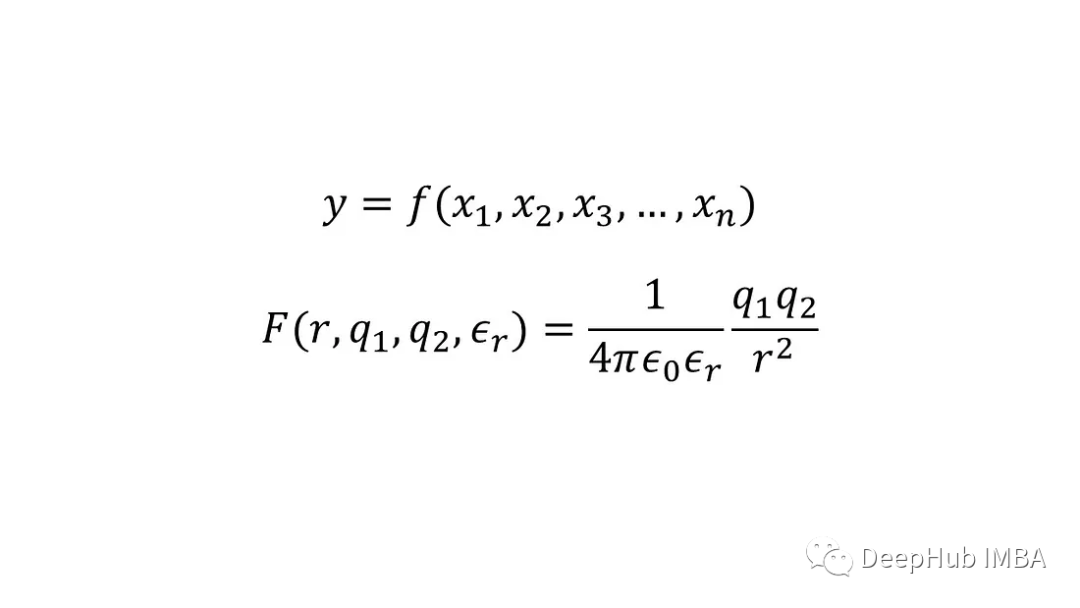
如果我们不知道这种关系，我们只有多个数据点，每个数据点都包括点电荷(输出)和相应的输入之间的相互作用，那么可以拟合人工神经网络来预测在具有指定介电常数的介质中任何给定分离的任何给定点电荷的相互作用，因为为物理问题创建数据驱动模型相对简单。

但是考虑从分子结构预测某一特定性质的问题，比如在水中的溶解度。没有一组明显的输入来描述一个分子，虽然可以使用各种特性，例如键长、键角、不同类型元素的数量、环的数量等等。但是并不能保证任何这样的任意集合一定能很好地适用于所有分子。

另外与点电荷的例子不同，输入不一定驻留在连续空间中。例如，我们可以把甲醇、乙醇和丙醇想象成一组链长不断增加的分子;链长是一个离散的参数，没有办法在甲醇和乙醇之间插入来得到其他分子。具有连续的输入空间对于计算模型的导数是必不可少的，然后可以用于所选属性的优化。

为了克服这些问题人们提出了各种分子编码方法。其中一种方法是使用SMILES和SELFIES等进行文本表示。关于这种表示有大量的文献，有兴趣的话可以搜索阅读。第二种方法是用图形表示分子。虽然每种方法都有其优点和缺点，但图形表示对化学来说更直观。

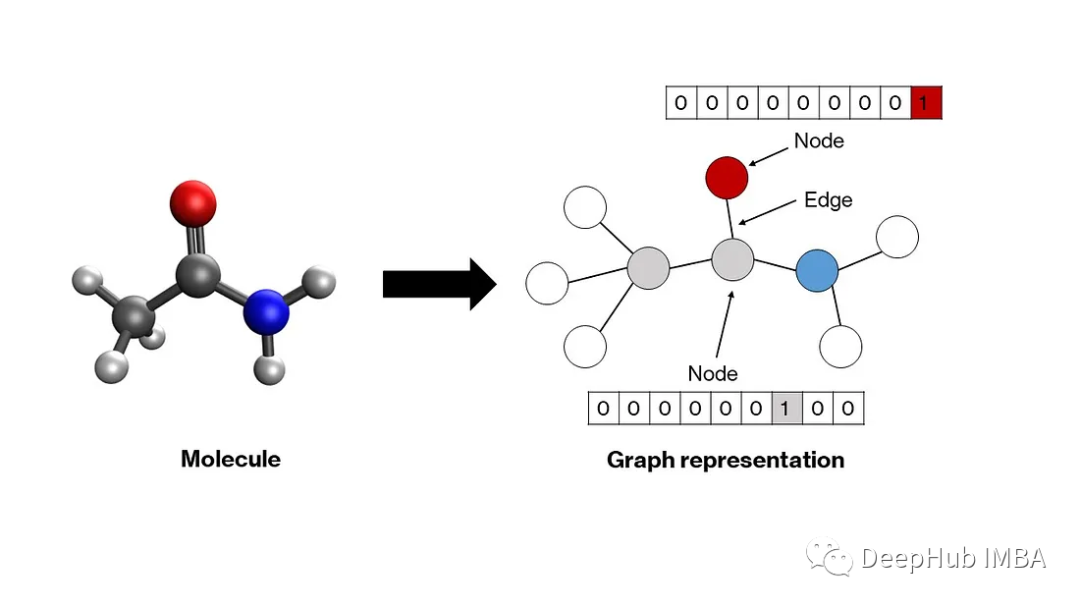
图是一种数学结构，由表示节点之间关系的边连接的节点组成。分子自然适应这种结构——原子成为节点，化学键成为边缘。图中的每个节点都由一个向量表示，该向量编码相应原子的属性。通常，独热编码模式就足够了(下一节将对此进行详细介绍)。这些向量可以堆叠以创建节点矩阵。节点之间的关系——用边表示——可以通过一个方形邻接矩阵来描述，其中每个元素a′′ⱼ要么是1，要么是0，这取决于两个节点i和j是否分别由边连接。对角线元素设置为1，表示自连接，这使得矩阵可以进行卷积。这些节点和邻接矩阵将作为我们模型的输入。

神经网络模型接受一维输入向量。对于多维输入，例如图像则使用一类称为卷积神经网络的模型。在我们的例子中，也是二维矩阵作为输入。图神经网络被开发用于操作这样的节点和邻接矩阵，将它们转换成合适的一维向量，然后可以通过普通人工神经网络的隐藏层来生成输出。有许多类型的图神经网络，如图卷积网络、消息传递网络、图注意网络等，它们的主要区别在于在图中的节点和边之间交换信息的方法不同。由于图卷积网络相对简单，我们将仔细研究它。

图卷积和池化层

输入的初始状态，节点矩阵表示每行中每个原子的独热编码，其中原子序数为n的原子在第n个索引处为1，在其他地方为0。邻接矩阵表示节点之间的连接。在当前状态下，节点矩阵不能作为人工神经网络的输入，因为:(1)它是二维的，(2)它不是置换不变的，(3)它不是唯一的。在这种情况下，排列不变性意味着无论你如何排列节点，输入都应该保持不变;同一分子可以由同一节点矩阵的多个排列表示(假设邻接矩阵中也有适当的排列)。

对于前两个问题，有一个简单的解决方案——池化。如果节点矩阵沿着列维度池化，那么它将被简化为一个排列不变的一维向量。通常，这种池化是一个简单的均值池化，这意味着最终的池化向量包含节点矩阵中每列的均值。但是池化两个异构体的节点矩阵，如正戊烷和新戊烷，将产生相同的池化向量，也就是说解决第三个问题还需要其他的方法。

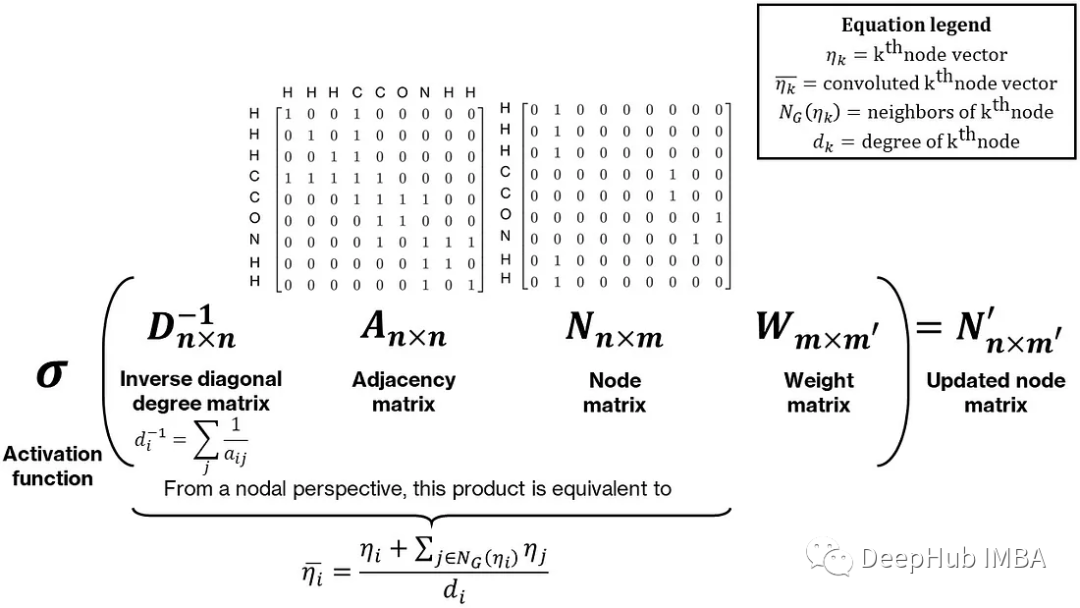
为了使最终的池化向量唯一，需要在节点矩阵中合并一些邻居信息。对于同分异构体，虽然它们的化学式相同，但它们的结构却不同。合并邻居信息的一种简单方法是对每个节点及其邻居执行一些操作，例如求和。这可以表示为节点和邻接矩阵的乘法：邻接矩阵乘以节点矩阵产生一个更新的节点矩阵，每个节点向量等于它的邻居节点向量与它自己的和，这个和通过预乘以对角度矩阵的逆，通过每个节点的度(或邻居的数量)进行归一化，使其成为邻居的平均值。最后这个乘积后乘一个权重矩阵，整个操作称为图卷积。下图显示了一个直观而简单的图卷积形式

Thomas Kipf和Max Welling的工作提供了一个数学上更严格和数值上更稳定的形式，使用邻接矩阵的修改归一化。卷积和池化操作的组合也可以被解释为经验群体贡献方法的非线性形式。

图卷积网络的最终结构如下:首先计算给定分子的节点矩阵和邻接矩阵，然后池化以产生包含有关分子的所有信息的单个向量。通过标准人工神经网络的隐藏层来产生输出。隐藏层、池化层和卷积层的权重通过应用于基于回归的损失函数(如均方损失)的反向传播同时确定。

Pytorch代码实现

上面我们讨论了图卷积网络相关的所有关键思想，下面开始使用PyTorch进行简单的实现。虽然有一个灵活的、高性能的gnn框架PyTorch Geometric，但我们不会使用它，因为我们的目标是深入我们的理解。

1、使用RDKit创建图

RDKit是一个化学信息学库，允许高通量访问小分子的特性。我们将需要它完成两个任务——将分子中每个原子的原子序数变为1——对节点矩阵进行编码并获得邻接矩阵。我们假设分子是根据它们的SMILES字符串提供的(这对于大多数化学信息学数据都是正确的)。为了确保节点矩阵和邻接矩阵的大小在所有分子中都是一致的（这在默认情况下是不可能的，因为两者的大小都取决于分子中的原子数量）我们用0填充矩阵。

除此以外我们将对上面提出的卷积进行一个小的修改——将邻接矩阵中的“1”替换为相应键长的倒数。通过这种方式，网络将获得更多关于分子几何形状的信息，并且它还将根据相邻键的长度对每个节点周围的卷积进行加权。

class Graph:
    def __init__(
        self, molecule_smiles: str,
        node_vec_len: int,
        max_atoms: int = None
      ):
        # Store properties
        self.smiles = molecule_smiles
        self.node_vec_len = node_vec_len
        self.max_atoms = max_atoms
 
        # Call helper function to convert SMILES to RDKit mol
        self.smiles_to_mol()
 
        # If valid mol is created, generate a graph of the mol
        if self.mol is not None:
            self.smiles_to_graph()
 
    def smiles_to_mol(self):
        # Use MolFromSmiles from RDKit to get molecule object
        mol = Chem.MolFromSmiles(self.smiles)
         
        # If a valid mol is not returned, set mol as None and exit
        if mol is None:
            self.mol = None
            return
 
        # Add hydrogens to molecule
        self.mol = Chem.AddHs(mol)
 
    def smiles_to_graph(self):
        # Get list of atoms in molecule
        atoms = self.mol.GetAtoms()
 
        # If max_atoms is not provided, max_atoms is equal to maximum number 
        # of atoms in this molecule. 
        if self.max_atoms is None:
            n_atoms = len(list(atoms))
        else:
            n_atoms = self.max_atoms
 
        # Create empty node matrix
        node_mat = np.zeros((n_atoms, self.node_vec_len))
 
        # Iterate over atoms and add to node matrix
        for atom in atoms:
            # Get atom index and atomic number
            atom_index = atom.GetIdx()
            atom_no = atom.GetAtomicNum()
 
            # Assign to node matrix
            node_mat[atom_index, atom_no] = 1
 
        # Get adjacency matrix using RDKit
        adj_mat = rdmolops.GetAdjacencyMatrix(self.mol)
        self.std_adj_mat = np.copy(adj_mat)
 
        # Get distance matrix using RDKit
        dist_mat = molDG.GetMoleculeBoundsMatrix(self.mol)
        dist_mat[dist_mat == 0.] = 1
 
        # Get modified adjacency matrix with inverse bond lengths
        adj_mat = adj_mat * (1 / dist_mat)
 
        # Pad the adjacency matrix with 0s
        dim_add = n_atoms - adj_mat.shape[0]
        adj_mat = np.pad(
            adj_mat, pad_width=((0, dim_add), (0, dim_add)), mode="constant"
        )
 
        # Add an identity matrix to adjacency matrix
        # This will make an atom its own neighbor
        adj_mat = adj_mat + np.eye(n_atoms)
 
        # Save both matrices
        self.node_mat = node_mat
        self.adj_mat = adj_mat

2、在生成Dataset

PyTorch提供了一个方便的Dataset类来存储和访问各种数据。我们将用它来获取节点和邻接矩阵以及每个分子的输出。

class GraphData(Dataset):
    def __init__(self, dataset_path: str, node_vec_len: int, max_atoms: int):
        # Save attributes
        self.node_vec_len = node_vec_len
        self.max_atoms = max_atoms
 
        # Open dataset file
        df = pd.read_csv(dataset_path)
 
        # Create lists
        self.indices = df.index.to_list()
        self.smiles = df["smiles"].to_list()
        self.outputs = df["measured log solubility in mols per litre"].to_list()
 
    def __len__(self):
        return len(self.indices)
 
    def __getitem__(self, i: int):
        # Get smile
        smile = self.smiles[i]
 
        # Create MolGraph object using the Graph abstraction
        mol = Graph(smile, self.node_vec_len, self.max_atoms)
 
        # Get node and adjacency matrices
        node_mat = torch.Tensor(mol.node_mat)
        adj_mat = torch.Tensor(mol.adj_mat)
 
        # Get output
        output = torch.Tensor([self.outputs[i]])
 
        return (node_mat, adj_mat), output, smile

除此以外，我们还需要自定义collate函数，来使得dataset可以进行批处理，也就是说把单一的dataset合并成一个batch

def collate_graph_dataset(dataset: Dataset):
    # Create empty lists of node and adjacency matrices, outputs, and smiles
    node_mats = []
    adj_mats = []
    outputs = []
    smiles = []
     
    # Iterate over list and assign each component to the correct list
    for i in range(len(dataset)):
        (node_mat,adj_mat), output, smile = dataset[i]
        node_mats.append(node_mat)
        adj_mats.append(adj_mat)
        outputs.append(output)
        smiles.append(smile)
     
         
    # Create tensors
    node_mats_tensor = torch.cat(node_mats, dim=0)
    adj_mats_tensor = torch.cat(adj_mats, dim=0)
    outputs_tensor = torch.stack(outputs, dim=0)
     
    # Return tensors
    return (node_mats_tensor, adj_mats_tensor), outputs_tensor, smiles

3、图卷积网络

在完成了数据处理之后现在可以构建模型了，这里为了学习将构建自己的卷积层和池化层，但如果在实际使用时可以直接使用PyTorch Geometric模块。卷积层基本上做三件事-(1)计算邻接矩阵的反对角度矩阵，(2)四个矩阵的乘法(D⁻¹ANW)，(3)对层输出应用非线性激活函数。与其他PyTorch类一样，我们将继承Module基类。

class ConvolutionLayer(nn.Module):
    def __init__(self, node_in_len: int, node_out_len: int):
        # Call constructor of base class
        super().__init__()
 
        # Create linear layer for node matrix
        self.conv_linear = nn.Linear(node_in_len, node_out_len)
 
        # Create activation function
        self.conv_activation = nn.LeakyReLU()
 
    def forward(self, node_mat, adj_mat):
        # Calculate number of neighbors
        n_neighbors = adj_mat.sum(dim=-1, keepdims=True)
        # Create identity tensor
        self.idx_mat = torch.eye(
            adj_mat.shape[-2], adj_mat.shape[-1], device=n_neighbors.device
        )
        # Add new (batch) dimension and expand
        idx_mat = self.idx_mat.unsqueeze(0).expand(*adj_mat.shape)
        # Get inverse degree matrix
        inv_degree_mat = torch.mul(idx_mat, 1 / n_neighbors)
 
        # Perform matrix multiplication: D^(-1)AN
        node_fea = torch.bmm(inv_degree_mat, adj_mat)
        node_fea = torch.bmm(node_fea, node_mat)
 
        # Perform linear transformation to node features 
        # (multiplication with W)
        node_fea = self.conv_linear(node_fea)
 
        # Apply activation
        node_fea = self.conv_activation(node_fea)
 
        return node_fea

接下来，让我们构造只执行一个操作，即沿第二维(节点数)取平均值的PoolingLayer层。

class PoolingLayer(nn.Module):
    def __init__(self):
        # Call constructor of base class
        super().__init__()
 
    def forward(self, node_fea):
        # Pool the node matrix
        pooled_node_fea = node_fea.mean(dim=1)
        return pooled_node_fea

最后就是创建包含卷积层、池化层和隐藏层的ChemGCN类。我们将对所有的层输出应用LeakyReLU激活函数，还将使用dropout来最小化过拟合。

class ChemGCN(nn.Module):
    def __init__(
        self,
        node_vec_len: int,
        node_fea_len: int,
        hidden_fea_len: int,
        n_conv: int,
        n_hidden: int,
        n_outputs: int,
        p_dropout: float = 0.0,
    ):
        # Call constructor of base class
        super().__init__()
 
        # Define layers
        # Initial transformation from node matrix to node features
        self.init_transform = nn.Linear(node_vec_len, node_fea_len)
 
        # Convolution layers
        self.conv_layers = nn.ModuleList(
            [
                ConvolutionLayer(
                    node_in_len=node_fea_len,
                    node_out_len=node_fea_len,
                )
                for i in range(n_conv)
            ]
        )
 
        # Pool convolution outputs
        self.pooling = PoolingLayer()
        pooled_node_fea_len = node_fea_len
 
        # Pooling activation
        self.pooling_activation = nn.LeakyReLU()
 
        # From pooled vector to hidden layers
        self.pooled_to_hidden = nn.Linear(pooled_node_fea_len, hidden_fea_len)
 
        # Hidden layer
        self.hidden_layer = nn.Linear(hidden_fea_len, hidden_fea_len)
 
        # Hidden layer activation function
        self.hidden_activation = nn.LeakyReLU()
 
        # Hidden layer dropout
        self.dropout = nn.Dropout(p=p_dropout)
 
        # If hidden layers more than 1, add more hidden layers
        self.n_hidden = n_hidden
        if self.n_hidden > 1:
            self.hidden_layers = nn.ModuleList(
                [self.hidden_layer for _ in range(n_hidden - 1)]
            )
            self.hidden_activation_layers = nn.ModuleList(
                [self.hidden_activation for _ in range(n_hidden - 1)]
            )
            self.hidden_dropout_layers = nn.ModuleList(
                [self.dropout for _ in range(n_hidden - 1)]
            )
 
        # Final layer going to the output
        self.hidden_to_output = nn.Linear(hidden_fea_len, n_outputs)
 
    def forward(self, node_mat, adj_mat):
        # Perform initial transform on node_mat
        node_fea = self.init_transform(node_mat)
 
        # Perform convolutions
        for conv in self.conv_layers:
            node_fea = conv(node_fea, adj_mat)
 
        # Perform pooling
        pooled_node_fea = self.pooling(node_fea)
        pooled_node_fea = self.pooling_activation(pooled_node_fea)
 
        # First hidden layer
        hidden_node_fea = self.pooled_to_hidden(pooled_node_fea)
        hidden_node_fea = self.hidden_activation(hidden_node_fea)
        hidden_node_fea = self.dropout(hidden_node_fea)
 
        # Subsequent hidden layers
        if self.n_hidden > 1:
            for i in range(self.n_hidden - 1):
                hidden_node_fea = self.hidden_layers[i](hidden_node_fea)
                hidden_node_fea = self.hidden_activation_layers[i](hidden_node_fea)
                hidden_node_fea = self.hidden_dropout_layers[i](hidden_node_fea)
 
        # Output
        out = self.hidden_to_output(hidden_node_fea)
 
        return out

4、训练

最后就是编写辅助函数来训练和测试我们的模型，并编写脚本来运行一个制作图形、构建网络和训练模型的工作流。

首先，我们将定义一个标准化类来标准化输出，这有助于快速收敛

class Standardizer:
    def __init__(self, X):
        self.mean = torch.mean(X)
        self.std = torch.std(X)
 
    def standardize(self, X):
        Z = (X - self.mean) / (self.std)
        return Z
 
    def restore(self, Z):
        X = self.mean + Z * self.std
        return X
 
    def state(self):
        return {"mean": self.mean, "std": self.std}
 
    def load(self, state):
        self.mean = state["mean"]
        self.std = state["std"]

然后就是我们的训练过程：

def train_model(
    epoch,
    model,
    training_dataloader,
    optimizer,
    loss_fn,
    standardizer,
    use_GPU,
    max_atoms,
    node_vec_len,
 ):
    # Create variables to store losses and error
    avg_loss = 0
    avg_mae = 0
    count = 0
 
    # Switch model to train mode
    model.train()
 
    # Go over each batch in the dataloader
    for i, dataset in enumerate(training_dataloader):
        # Unpack data
        node_mat = dataset[0][0]
        adj_mat = dataset[0][1]
        output = dataset[1]
 
        # Reshape inputs
        first_dim = int((torch.numel(node_mat)) / (max_atoms * node_vec_len))
        node_mat = node_mat.reshape(first_dim, max_atoms, node_vec_len)
        adj_mat = adj_mat.reshape(first_dim, max_atoms, max_atoms)
 
        # Standardize output
        output_std = standardizer.standardize(output)
 
        # Package inputs and outputs; check if GPU is enabled
        if use_GPU:
            nn_input = (node_mat.cuda(), adj_mat.cuda())
            nn_output = output_std.cuda()
        else:
            nn_input = (node_mat, adj_mat)
            nn_output = output_std
 
        # Compute output from network
        nn_prediction = model(*nn_input)
 
        # Calculate loss
        loss = loss_fn(nn_output, nn_prediction)
        avg_loss += loss
 
        # Calculate MAE
        prediction = standardizer.restore(nn_prediction.detach().cpu())
        mae = mean_absolute_error(output, prediction)
        avg_mae += mae
 
        # Set zero gradients for all tensors
        optimizer.zero_grad()
 
        # Do backward prop
        loss.backward()
 
        # Update optimizer parameters
        optimizer.step()
 
        # Increase count
        count += 1
 
    # Calculate avg loss and MAE
    avg_loss = avg_loss / count
    avg_mae = avg_mae / count
 
    # Print stats
    print(
        "Epoch: [{0}]\tTraining Loss: [{1:.2f}]\tTraining MAE: [{2:.2f}]"\
            .format(
                    epoch, avg_loss, avg_mae
            )
    )
 
    # Return loss and MAE
    return avg_loss, avg_mae

最后，这个脚本将调用上面定义的所有内容。

#### Fix seeds
 np.random.seed(0)
 torch.manual_seed(0)
 use_GPU = torch.cuda.is_available()
 
 #### Inputs
 max_atoms = 200
 node_vec_len = 60
 train_size = 0.7
 batch_size = 32
 hidden_nodes = 60
 n_conv_layers = 4
 n_hidden_layers = 2
 learning_rate = 0.01
 n_epochs = 50
 
 #### Start by creating dataset
 main_path = Path(__file__).resolve().parent
 data_path = main_path / "data" / "solubility_data.csv"
 dataset = GraphData(dataset_path=data_path, max_atoms=max_atoms, 
                        node_vec_len=node_vec_len)
 
 #### Split data into training and test sets
 # Get train and test sizes
 dataset_indices = np.arange(0, len(dataset), 1)
 train_size = int(np.round(train_size * len(dataset)))
 test_size = len(dataset) - train_size
 
 # Randomly sample train and test indices
 train_indices = np.random.choice(dataset_indices, size=train_size, 
                                                            replace=False)
 test_indices = np.array(list(set(dataset_indices) - set(train_indices)))
 
 # Create dataoaders
 train_sampler = SubsetRandomSampler(train_indices)
 test_sampler = SubsetRandomSampler(test_indices)
 train_loader = DataLoader(dataset, batch_size=batch_size, 
                          sampler=train_sampler, 
                          collate_fn=collate_graph_dataset)
 test_loader = DataLoader(dataset, batch_size=batch_size, 
                          sampler=test_sampler,
                          collate_fn=collate_graph_dataset)
 
 #### Initialize model, standardizer, optimizer, and loss function
 # Model
 model = ChemGCN(node_vec_len=node_vec_len, node_fea_len=hidden_nodes,
                hidden_fea_len=hidden_nodes, n_cnotallow=n_conv_layers, 
                n_hidden=n_hidden_layers, n_outputs=1, p_dropout=0.1)
 # Transfer to GPU if needed
 if use_GPU:
    model.cuda()
 
 # Standardizer
 outputs = [dataset[i][1] for i in range(len(dataset))]
 standardizer = Standardizer(torch.Tensor(outputs))
 
 # Optimizer
 optimizer = torch.optim.Adam(model.parameters(), lr=learning_rate)
 
 # Loss function
 loss_fn = torch.nn.MSELoss()
 
 #### Train the model
 loss = []
 mae = []
 epoch = []
 for i in range(n_epochs):
    epoch_loss, epoch_mae = train_model(
        i,
        model,
        train_loader,
        optimizer,
        loss_fn,
        standardizer,
        use_GPU,
        max_atoms,
        node_vec_len,
    )
    loss.append(epoch_loss)
    mae.append(epoch_mae)
    epoch.append(i)
 
 #### Test the model
 # Call test model function
 test_loss, test_mae = test_model(model, test_loader, loss_fn, standardizer,
                                  use_GPU, max_atoms, node_vec_len)
 
 #### Print final results
 print(f"Training Loss: {loss[-1]:.2f}")
 print(f"Training MAE: {mae[-1]:.2f}")
 print(f"Test Loss: {test_loss:.2f}")
 print(f"Test MAE: {test_mae:.2f}")

结果

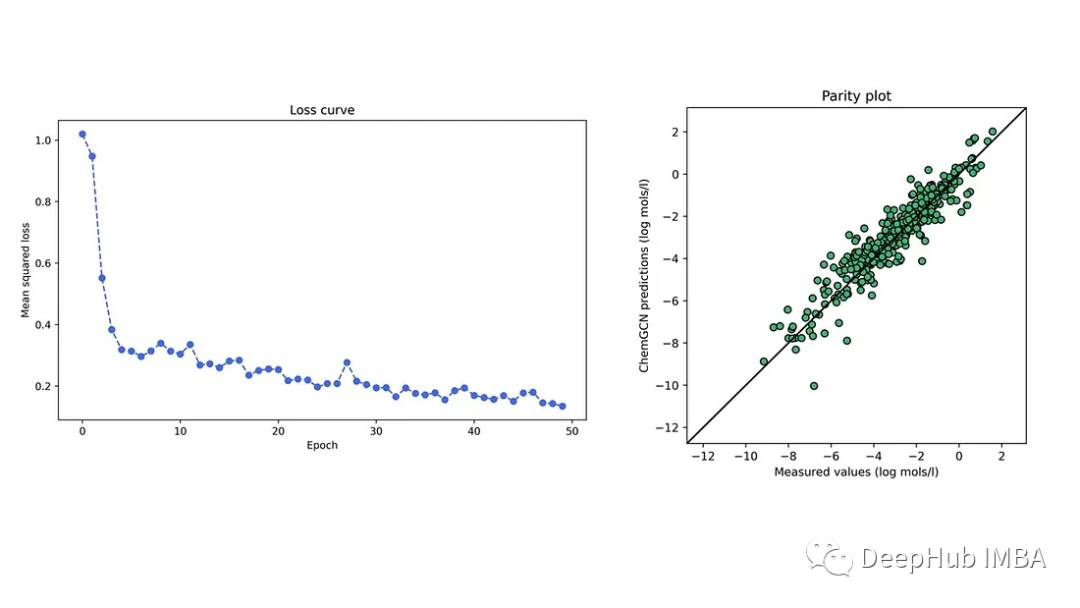
我们在开源DeepChem存储库的溶解度数据集上进行训练，该存储库包含约1000个小分子的水溶性。下图显示了一个特定训练-测试分层的测试集的训练损失曲线图。训练集和测试集的平均绝对误差分别为0.59和0.58 (log mol/l)，低于线性模型的0.69 log mol/l(基于数据集中的预测)。可以看到神经网络比线性回归模型表现得更好;这种比较虽然粗略，但是我们的模型所做的预测是合理的。

总结

我们通过一个简单的化学问题介绍了图卷积网络的基本原理，实现了自己的网络，并且对比基类模型，证明了我们模型的有效性，这是我们学习GCN的第一步。

本文完整的代码在GitHub地址如下：

https://github.com/gauravsdeshmukh/ChemGCN

数据集：

https://github.com/deepchem/deepchem