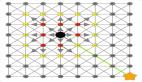
寻路算法是计算机图形学和人工智能领域中常用的算法之一，用于计算从一个点到另一个点的最短路径或最优路径。在本文中，我将详细介绍两种常用的寻路算法：Dijkstra算法和A*算法。
Dijkstra算法
Dijkstra算法是一种广度优先搜索算法，用于寻找图中两点之间的最短路径。算法的思路如下：
创建一个集合S，用于存放已经找到最短路径的顶点。
创建一个集合Q，用于存放还未找到最短路径的顶点。
初始化距离数组dist，将起始点到其余点的距离设置为无穷大，起始点到自身的距离设置为0。
重复以下步骤，直到集合Q为空：
- 在集合Q中找到距离起始点最近的顶点u，并将其加入集合S。
- 对于顶点u的每个邻居顶点v，更新起始点到v的距离dist[v]，如果dist[v] > dist[u] + edge(u, v)，则更新dist[v]为dist[u] + edge(u, v)。
最终，dist数组中存储的就是起始点到各个顶点的最短路径。
下面是使用C#实现的Dijkstra算法的源代码：
class DijkstraAlgorithm
{
private int[,] graph;
private int size;
public DijkstraAlgorithm(int[,] graph)
{
this.graph = graph;
this.size = graph.GetLength(0);
}
public int[] FindShortestPath(int start, int end)
{
int[] dist = new int[size];
bool[] visited = new bool[size];
for (int i = 0; i < size; i++)
{
dist[i] = int.MaxValue;
visited[i] = false;
}
dist[start] = 0;
for (int count = 0; count < size - 1; count++)
{
int u = GetMinDistance(dist, visited);
visited[u] = true;
for (int v = 0; v < size; v++)
{
if (!visited[v] && graph[u, v] != 0 && dist[u] != int.MaxValue
&& dist[u] + graph[u, v] < dist[v])
{
dist[v] = dist[u] + graph[u, v];
}
}
}
return dist;
}
private int GetMinDistance(int[] dist, bool[] visited)
{
int minDist = int.MaxValue;
int minIndex = -1;
for (int v = 0; v < size; v++)
{
if (!visited[v] && dist[v] <= minDist)
{
minDist = dist[v];
minIndex = v;
}
}
return minIndex;
}
}A算法
A算法是一种启发式搜索算法，用于寻找图中两点之间的最短路径。算法的思路如下：
创建一个优先队列openSet，用于存放待探索的顶点。
创建一个数组gScore，用于存放起始点到每个顶点的实际代价。
创建一个数组fScore，用于存放起始点通过每个顶点到达目标点的估计代价。
将起始点加入openSet，并将gScore[start]设置为0，fScore[start]设置为起始点到目标点的估计代价。
重复以下步骤，直到openSet为空：
- 在openSet中找到fScore最小的顶点current。
- 如果current等于目标点，表示已经找到最短路径，返回路径。
- 将current从openSet中移除。
- 对于current的每个邻居顶点neighbor，计算从起始点到neighbor的实际代价tempGScore，如果tempGScore小于gScore[neighbor]，更新gScore[neighbor]为tempGScore，并计算fScore[neighbor] = gScore[neighbor] + 估计代价。如果neighbor不在openSet中，将其加入openSet。
如果openSet为空，表示无法到达目标点，返回空。
下面是使用Java实现的A*算法的源代码：
import java.util.*;
class AStarAlgorithm {
private int[][] graph;
private int size;
public AStarAlgorithm(int[][] graph) {
this.graph = graph;
this.size = graph.length;
}
public List<Integer> findShortestPath(int start, int end) {
PriorityQueue<Node> openSet = new PriorityQueue<>();
int[] gScore = new int[size];
int[] fScore = new int[size];
int[] cameFrom = new int[size];
boolean[] visited = new boolean[size];
Arrays.fill(gScore, Integer.MAX_VALUE);
Arrays.fill(fScore, Integer.MAX_VALUE);
Arrays.fill(cameFrom, -1);
gScore[start] = 0;
fScore[start] = heuristicCostEstimate(start, end);
openSet.offer(new Node(start, fScore[start]));
while (!openSet.isEmpty()) {
int current = openSet.poll().index;
if (current == end) {
return reconstructPath(cameFrom, current);
}
visited[current] = true;
for (int neighbor = 0; neighbor < size; neighbor++) {
if (graph[current][neighbor] != 0 && !visited[neighbor]) {
int tempGScore = gScore[current] + graph[current][neighbor];
if (tempGScore < gScore[neighbor]) {
cameFrom[neighbor] = current;
gScore[neighbor] = tempGScore;
fScore[neighbor] = gScore[neighbor] + heuristicCostEstimate(neighbor, end);
if (!openSet.contains(new Node(neighbor, fScore[neighbor]))) {
openSet.offer(new Node(neighbor, fScore[neighbor]));
}
}
}
}
}
return null;
}
private int heuristicCostEstimate(int start, int end) {
// 估计代价的计算方法，例如欧几里得距离、曼哈顿距离等
return Math.abs(end - start);
}
private List<Integer> reconstructPath(int[] cameFrom, int current) {
List<Integer> path = new ArrayList<>();
path.add(current);
while (cameFrom[current] != -1) {
current = cameFrom[current];
path.add(0, current);
}
return path;
}
private class Node implements Comparable<Node> {
public int index;
public int fScore;
public Node(int index, int fScore) {
this.index = index;
this.fScore = fScore;
}
@Override
public int compareTo(Node other) {
return Integer.compare(this.fScore, other.fScore);
}
@Override
public boolean equals(Object obj) {
if (this == obj) {
return true;
}
if (obj == null || getClass() != obj.getClass()) {
return false;
}
Node other = (Node) obj;
return index == other.index;
}
@Override
public int hashCode() {
return Objects.hash(index);
}
}
}以上是对Dijkstra算法和A*算法的详细介绍，包括算法思路、过程和使用C#或Java实现的源代码。这两种算法都是常用的寻路算法，可以根据具体需求选择使用。
当然在现在的城市里导航软件软件可以给我们规划好。
