天气渐寒,大家做好保暖措施。反正我在武汉是被冻傻了😪。
首先,做任何有关回溯的题,一定要把这个递归函数模板记在心里!!
void backtracking(参数) {
if (终止条件) {
存放结果;
return;
}
for (选择本层集合中元素(画成树,就是树节点孩子的大小)){
处理节点;
backtracking();
回溯,撤销处理结果;
}
}组合总和问题
LeetCode 39:给你一个无重复元素的整数数组candidates和一个目标整数 target ,找出 candidates 中可以使数字和为目标数 target 的 所有不同组合 ,并以列表形式返回。你可以按任意顺序返回这些组合。candidates 中的 同一个 数字可以 无限制重复被选取 。如果至少一个数字的被选数量不同,则两种组合是不同的。数组中的元素满足1 <= candidates[i] <= 200。
示例:
- 输入:candidates = [2,3,6,7],target = 7
- 输出:[[2,2,3],[7]]
- 解释:2 和 3 可以形成一组候选,2 + 2 + 3 = 7 。注意2可以使用多次。7 也是一个候选, 7 = 7 ,仅有这两种组合。
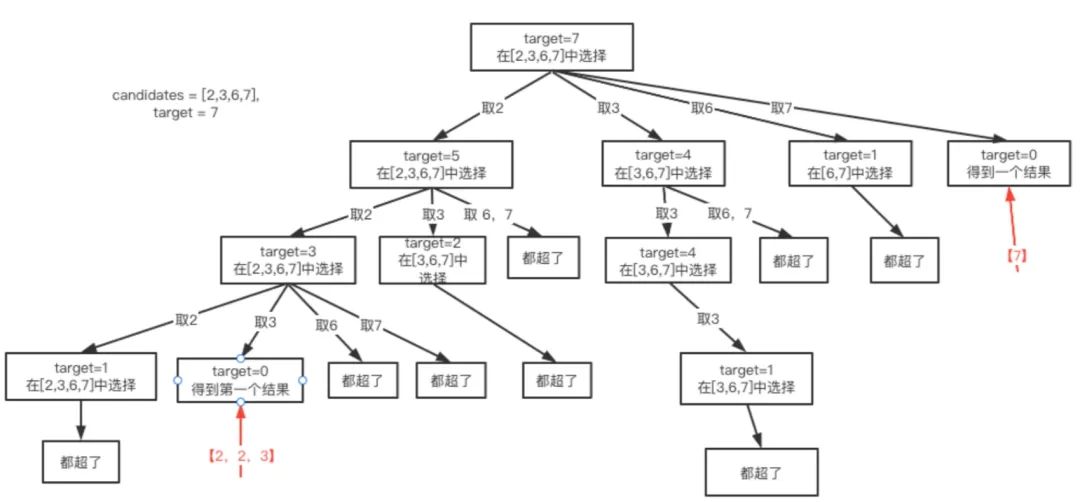
分析:首先,对于序列{2,3,6,7},target=7。可以先选2,然后剩下的target就是7-2=5。再选一个2,剩余5-2=3。之后再选一个2,剩余3-2=1。已经小于2了,我们不能继续向下了,要撤回一下,看有没有3。有3,就得到了第一个结果{2,2,3}。
然后,撤回到只选了一个2的时候,这时不能再取2了,而是从{3,6,7}中选择,如下图所示,没有符合要求的!以此类推,后面尝试从3、6和7开始选择。
 图片
图片
所以我们最终得到的结果就是{2,2,3}和{2,5}。
这个图横向是针对每个元素的暴力枚举,纵向是递归,也是一个纵横问题。
List<List<Integer>> res = new ArrayList<>(); //结果数组
List<Integer> path = new ArrayList<>(); //记录当前正在访问的路径
public List<List<Integer>> combinationSum(int[] candidates, int target) {
dfs(candidates,0,target);
return res;
}
public void dfs(int[] c,int u,int target){
if(target < 0) return;
if(target == 0){
res.add(new ArrayList(path));
return;
}
for(int i = u ; i < c.length;i++){
if(c[i] <= target){
path.add(c[i]);
dfs(c,i,target-c[i]);
path.remove(path.size() - 1);
}
}
}配合上文提到的回溯模板你就会发现,这简直就是标准的回溯题目。
分割字符串
LeetCode 131:给你一个字符串 s,请你将 s 分割成一些子串,使每个子串都是回文串。返回 s 所有可能的分割方案。
示例 1:
- 输入:s = "aab"
- 输出:[["a","a","b"],["aa","b"]]
示例 2:
- 输入:s = "a"
- 输出:[["a"]]
分析:每个子串都要是回文串,这个功能可以单独写一个函数用于判断一个字符串是不是回文串。那么这个函数怎么实现呢?很简单,利用双指针分别指向字符串的首尾,一起往中间遍历,一旦相同位置上的字符不相同就返回false,否则就默认返回true。
还要再解决一个问题:如何分割?
 图片
图片
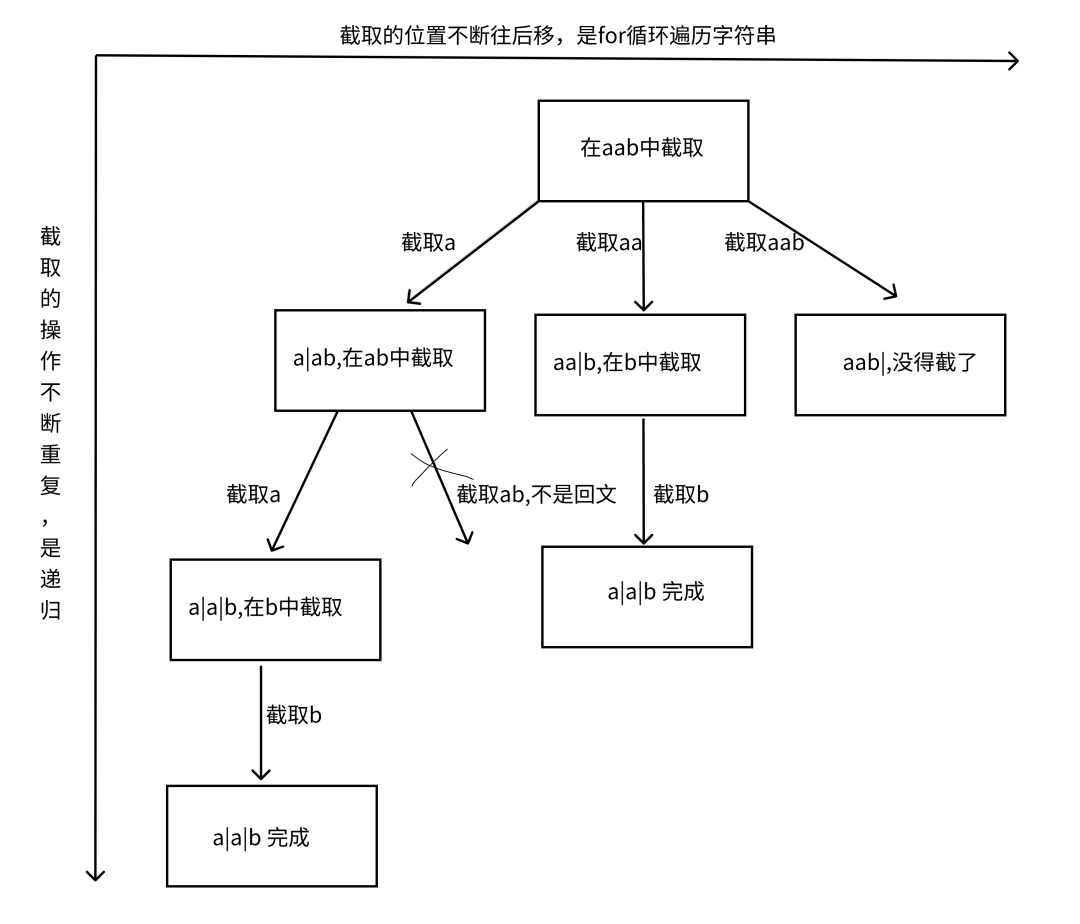
上图中,划竖线分开的就是每次分出的子串,右边就是还没分的。可见每次分出一个的时候我们都要判断一下是不是回文。
第一次切'a',第二次切'aa',第三次切'aab'。这对应的就是回溯里的for循环,也就是横向方面。第一次切了'a',剩下的就是'ab'。递归就是再将其再切一个回文下来,也就是第二个'a',剩下的'b'再交给递归进一步切割。这就是纵向方面要干的事情,其他以此类推。
用一个二维数组lists保存最后的结果。回想我们回溯的模板。首先想明白他的终止条件是什么?答:整个字符串都遍历完之后。for循环就是图中横向的那一部分。回溯,就是处理完这种方案之后,退回的第一层,开始下一种分割方案。
List<List<String>> lists = new ArrayList<>();
Deque<String> deque = new LinkedList<>();
public List<List<String>> partition(String s) {
backTracking(s, 0);
return lists;
}
private void backTracking(String s, int startIndex) {
//如果起始位置大于s的大小,说明找到了一组分割方案
if(startIndex >= s.length()){
lists.add(new ArrayList(deque));
return;
}
for(int i = startIndex;i < s.length();i++){
if(isPalindrome(s,startIndex,i)){
String str = s.substring(startIndex,i+1);
deque.addLast(str);
}else{
continue;
}
//起始位置后移,保证不重复
backTracking(s,i+1);
deque.removeLast();
}
}
private boolean isPalindrome(String s,int startIndex,int end){
for(int i = startIndex, j = end;i < j;i++ , j--){
if(s.charAt(i) != s.charAt(j)){
return false;
}
}
return true;
}看到这你依旧是蒙蒙?没事,俺也一样!(抱拳)这在力扣上都会被怀疑是不是困难题啊哈哈哈哈。
 图片
图片
没事没事,我第一次的时候调代码就调了半天,很正常,我一点事都没有😎。



























