在数据科学和机器学习领域，许多模型都假设数据呈现正态分布，或者假设数据在正态分布下表现更好。例如，线性回归假设残差呈正态分布，线性判别分析（LDA）基于正态分布等假设进行推导。 因此，了解如何测试数据正态性的方法对于数据科学家和机器学习从业者至关重要。
本文将介绍测试数据正态性的11种基本方法，帮助读者更好地理解数据分布的特征和如何应用合适的方法进行分析，以便在机器学习和数据建模过程中更好地处理数据分布对模型性能的影响。
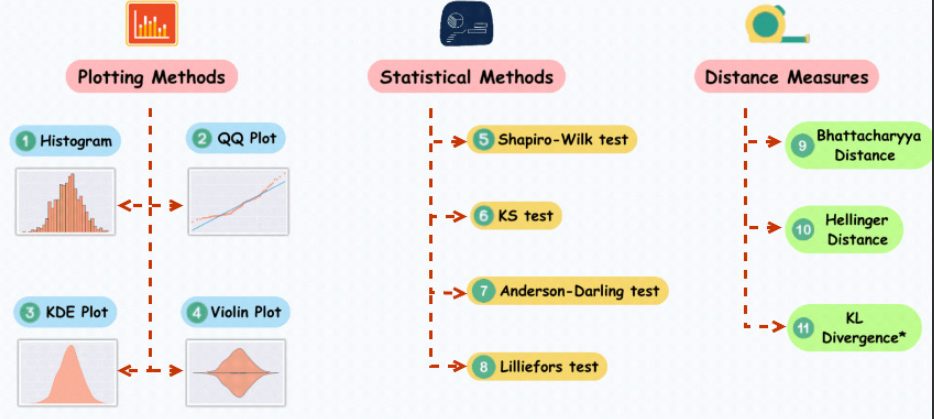
绘图法Plotting Methods
1.QQ Plot
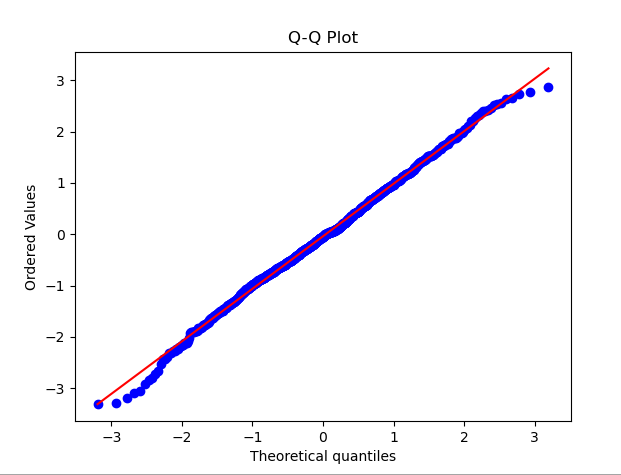
QQ图（Quantile-Quantile Plot）是一种用于检验数据分布是否符合正态分布的常用方法。在QQ图中，将数据的分位数与标准正态分布的分位数进行比较，如果数据分布接近正态分布，QQ图上的点将大致落在一条直线上。
如下示例代码生成了一组服从正态分布的随机数据来演示QQ Plot，运行代码后，既可看到QQ Plot以及与之对应的正态分布曲线，通过观察图上的点的分布情况来初步判断数据是否接近正态分布。
import numpy as np
import scipy.stats as stats
import matplotlib.pyplot as plt
# 生成一组随机数据，假设它们服从正态分布
data = np.random.normal(0, 1, 1000)
# 绘制QQ图
stats.probplot(data, dist="norm", plot=plt)
plt.title('Q-Q Plot')
plt.show()
2.KDE Plot
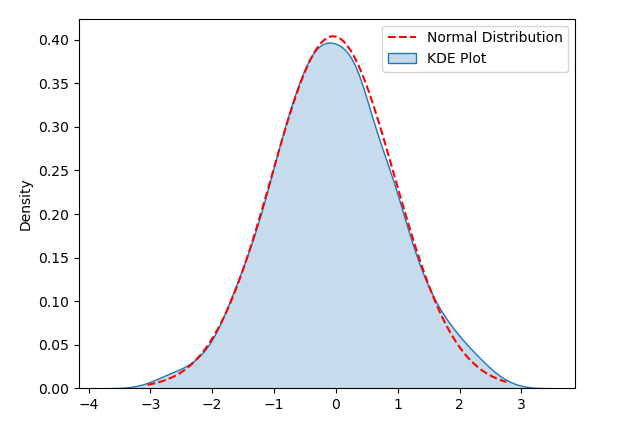
KDE（Kernel Density Estimation）Plot是一种用于可视化数据分布的方法，它可以帮助我们检测数据的正态性。在KDE Plot中，数据的密度被估计并绘制成一条平滑的曲线，这有助于我们观察数据的分布形状。
如下示例代码生成了一组服从正态分布的随机数据来演示KDE Plot，运行代码后，既可看到KDE Plot以及与之对应的正态分布曲线，从而通过可视化来检测数据分布的正态性。
import numpy as np
import seaborn as sns
import matplotlib.pyplot as plt
# 生成随机数据
np.random.seed(0)
data = np.random.normal(loc=0, scale=1, size=1000)
# 创建KDE Plot
sns.kdeplot(data, shade=True, label='KDE Plot')
# 添加正态分布曲线
mu, sigma = np.mean(data), np.std(data)
x = np.linspace(min(data), max(data), 100)
y = (1/(sigma * np.sqrt(2 * np.pi))) * np.exp(-0.5 * ((x - mu) / sigma) ** 2)
plt.plot(x, y, 'r--', label='Normal Distribution')
# 显示图表
plt.legend()
plt.show()
3.Violin Plot
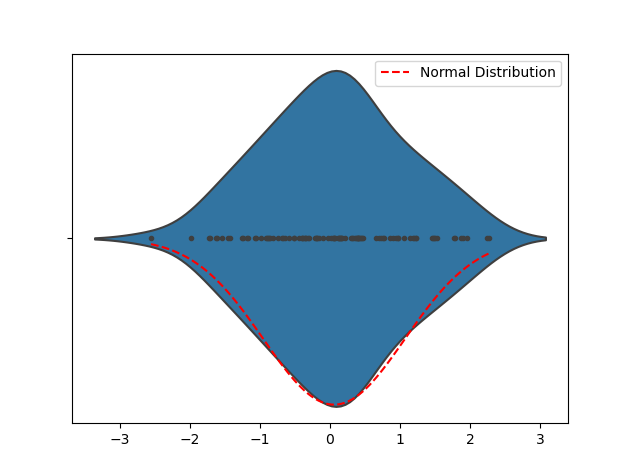
通过观察Violin Plot可以发现数据的分布形状，从而初步判断数据是否接近正态分布。如果 Violin Plot 呈现出类似钟形曲线的形状，那么数据可能是近似正态分布的。如果 Violin Plot 偏斜严重或者有多个峰值，那么数据可能不是正态分布的。
如下示例代码生成了一组服从正态分布的随机数据来演示Violin Plot，运行代码后，既可看到Violin Plot以及与之对应的正态分布曲线，通过可视化来检测数据分布的形状，从而初步判断数据是否接近正态分布。
import numpy as np
import seaborn as sns
import matplotlib.pyplot as plt
# 生成随机数据
np.random.seed(0)
data = np.random.normal(loc=0, scale=1, size=100)
# 创建 Violin Plot
sns.violinplot(data, inner="points")
# 添加正态分布曲线
mu, sigma = np.mean(data), np.std(data)
x = np.linspace(min(data), max(data), 100)
y = (1/(sigma * np.sqrt(2 * np.pi))) * np.exp(-0.5 * ((x - mu) / sigma) ** 2)
plt.plot(x, y, 'r--', label='Normal Distribution')
# 显示图表
plt.legend()
plt.show()
4.Histogram
使用直方图（Histogram）来检测数据分布的正态性也是一种常用的方法。直方图可以帮助你直观地了解数据的分布情况，并且可以初步判断数据是否接近正态分布。
import numpy as np
import matplotlib.pyplot as plt
import scipy.stats as stats
# 生成一组随机数据，假设它们服从正态分布
data = np.random.normal(0, 1, 1000)
# 绘制直方图
plt.hist(data, bins=30, density=True, alpha=0.6, color='g')
plt.title('Histogram of Data')
plt.xlabel('Value')
plt.ylabel('Frequency')
# 绘制正态分布的概率密度函数
xmin, xmax = plt.xlim()
x = np.linspace(xmin, xmax, 100)
p = stats.norm.pdf(x, np.mean(data), np.std(data))
plt.plot(x, p, 'k', linewidth=2)
plt.show()
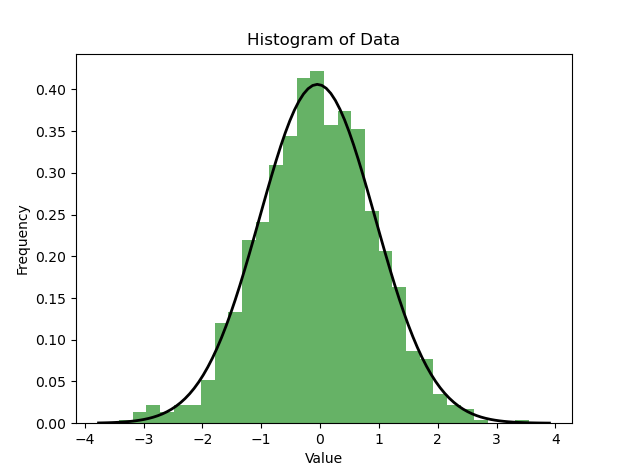
如上图所示，如果直方图近似呈现钟形曲线，并且与对应的正态分布曲线形状相似，那么数据可能符合正态分布。当然，可视化只是一种初步的判断，如果需要更精确的检测，可以结合使用正态性检验等统计方法进行分析。
统计方法Statistical Methods
5.夏皮罗一威尔克(Shapiro-Wilk)检验
是一种用于检验数据是否满足正态分布的统计方法，又称之为W检验。在进行Shapiro-Wilk检验时，我们通常会关注两个主要指标：
- 统计量W：基于观测数据与在正态分布下的期望值之间的相关性来计算统计量W，W的取值范围在0和1之间，当W接近1时，表示观测数据与正态分布的拟合程度较好。
- P值：P值表示观测到这种相关性的可能性，如果P值大于显著水平（通常为0.05），则表明观测数据很可能来自正态分布。
因此，当统计量W接近1且P值大于0.05时，我们可以得出结论：观测数据满足正态分布。
如下代码中，首先生成一组服从正态分布的随机数据，然后进行Shapiro-Wilk检验，得到检验统计量和P值。根据P值与显著性水平的比较，即可判断样本数据是否来自正态分布。
from scipy import stats
import numpy as np
# 生成一组服从正态分布的随机数据
data = np.random.normal(0, 1, 100)
# 执行Shapiro-Wilk检验
stat, p = stats.shapiro(data)
print('Shapiro-Wilk Statistic:', stat)
print('P-value:', p)
# 根据P值判断正态性
alpha = 0.05
if p > alpha:
print('样本数据可能来自正态分布')
else:
print('样本数据不符合正态分布')
6.KS检验
KS检验（Kolmogorov-Smirnov test）是一种用于检验数据是否符合特定分布（比如正态分布）的统计方法。它通过测量观测数据与特定理论分布的累积分布函数(CDF)之间的最大差异来评估二者是否来自同一分布。基本步骤如下：
- 对两个样本数据进行排序。
- 计算两个样本的经验累积分布函数(ECDF)，即计算每个值在样本中的累积百分比。
- 计算两个累积分布函数之间的差异，通常使用KS统计量衡量。
- 根据样本的大小和显著性水平，使用参考表活计算p值判断两个样本是否来自同一分布。
Python中使用KS检验来检验数据是否符合正态分布时，可以使用Scipy库中的kstest函数。下面是一个简单的示例，演示了如何使用Python进行KS检验来检验数据是否符合正态分布。
from scipy import stats
import numpy as np
# 生成一组服从正态分布的随机数据
data = np.random.normal(0, 1, 100)
# 执行KS检验
statistic, p_value = stats.kstest(data, 'norm')
print('KS Statistic:', statistic)
print('P-value:', p_value)
# 根据P值判断正态性
alpha = 0.05
if p_value > alpha:
print('样本数据可能来自正态分布')
else:
print('样本数据不符合正态分布')
7.Anderson-Darling检验
Anderson-Darling检验是一种用于检验数据是否来自特定分布（例如正态分布）的统计方法。它特别强调观察值在分布尾部的差异，因此在检测极端值的偏差方面非常有效。
如下代码使用stats.anderson函数执行Anderson-Darling检验，并获得检验统计量、临界值以及显著性水平。然后根据统计量与临界值的比较，即可判断样本数据是否来自正态分布。
from scipy import stats
import numpy as np
# 生成一组服从正态分布的随机数据
data = np.random.normal(0, 1, 100)
# 执行Anderson-Darling检验
result = stats.anderson(data, dist='norm')
print('Anderson-Darling Statistic:', result.statistic)
print('Critical Values:', result.critical_values)
print('Significance Level:', result.significance_level)
# 判断正态性
if result.statistic < result.critical_values[2]:
print('样本数据可能来自正态分布')
else:
print('样本数据不符合正态分布')
8.Lilliefors检验
Lilliefors检验（也称为Kolmogorov-Smirnov-Lilliefors检验）是一种用于检验数据是否符合正态分布的统计检验方法，它是Kolmogorov-Smirnov检验的一种变体，专门用于小样本情况。与K-S检验不同，Lilliefors检验不需要假定数据的分布类型，它基于观测数据来评估是否来自正态分布。
如下示例中，使用lilliefors函数执行Lilliefors检验，并获得检验统计量和P值。根据P值与显著性水平的比较，即可以判断样本数据是否来自正态分布。
import numpy as np
from statsmodels.stats.diagnostic import lilliefors
# 生成一组服从正态分布的随机数据
data = np.random.normal(0, 1, 100)
# 执行Lilliefors检验
statistic, p_value = lilliefors(data)
print('Lilliefors Statistic:', statistic)
print('P-value:', p_value)
# 根据P值判断正态性
alpha = 0.05
if p_value > alpha:
print('样本数据可能来自正态分布')
else:
print('样本数据不符合正态分布')
9.距离测量Distance Measures
距离测量（Distance measures）是一种有效的测试数据正态性的方法，它提供了更直观的方式来比较观察数据分布与参考分布之间的差异。
下面是一些常见的距离测量方法及其在测试正态性时的应用：
(1) 「巴氏距离（Bhattacharyya distance）」：
- 测量两个分布之间的重叠，通常被解释为两个分布之间的接近程度。
- 选择与观察到的分布具有最小Bhattacharyya距离的参考分布，作为最接近的分布。
(2) 「海林格距离（Hellinger distance）」：
- 用于衡量两个分布之间的相似度，类似于Bhattacharyya距离。
- 与Bhattacharyya距离不同的是，Hellinger距离满足三角不等式，这使得它在一些情况下更为实用。
(3) 「KL 散度（KL Divergence）」：
- 它本身并不是严格意义上的“距离度量”，但在测试正态性时可以用作衡量信息丢失的指标。
- 选择与观察到的分布具有最小KL散度的参考分布，作为最接近的分布。
这些距离测量方法可以帮助我们比较观察到的分布与多个参考分布之间的差异，从而更好地评估数据的正态性。通过选择与观察到的分布距离最小的参考分布，我们可以更准确地判断数据是否来自正态分布。
