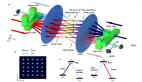
相比于常规的三通道 RGB 图像，高光谱图像包含几十上百个波段，从而捕获了关于成像场景更丰富的信息。也正因为这一重要特性，高光谱图像被广泛地应用于医疗，地形勘探，农业等领域。
如图1所示，在医院进行检查时，如果只看常规的RGB图像可能很难诊断病因，但是如果采用高光谱图像捕获并在特定波长下渲染的话，就可以看清楚各类血管，骨骼结构等，从而辅助医生诊断。同样的原理也可应用在遥感地形勘探和农业病虫害检测。
图1 高光谱图像的应用
然而高光谱图像并不容易获取，传统的成像设备采用光谱仪对成像场景进行逐波段的扫描，费时费力，难以捕捉运动场景。
近些年，科学家们专门设计了单曝光压缩成像（Snapshot Compressive Imaging，SCI）系统来解决这一问题。
其光路结构如图2所示。该系统首先通过一个编码孔径掩膜对成像场景的各光谱通道进行调制，然后通过一个三棱镜进行色散后在相机上捕获到一个二维的快照估计图（compressive measurement）。
通过这个光路系统，我们便可将三维的光谱立方块压缩成一个二维的图像。而光谱压缩重建的任务便是从这个二维的压缩估计图上恢复出三维的高光谱数据。
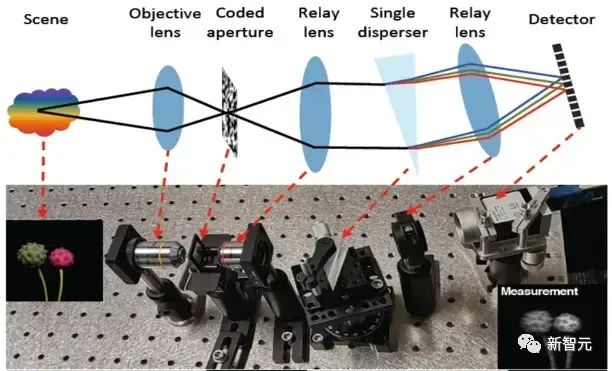图2 单曝光压缩成像系统
当前的主流方法是采用的是全精度模型如 CNN 或者 Transformer 来学一个从压缩估计图到三维光谱立方块的映射。几个比较经典算法有我们之前的工作 MST，MST++，CST，DAUHST，HDNet 等（这些方法全部都开源在我们的工具箱 MST 当中）。
这类方法虽然取得了很好的重建效果，但却难以部署到移动端设备（如智能手机、相机、无人机等）上，因为移动端设备的内存空间，计算资源和电力均有限，无法运转全精度模型。
另一方面，全精度模型的一些计算单元如深度展开算子和多头自注意力机制等相对复杂，移动端设备无法支持。
为了推动光谱重建算法的实际应用，清华大学等机构的研究人员提出了一个全新的工作，其主要贡献为：
图片
论文链接：https://arxiv.org/abs/2305.10299
代码链接：https://github.com/caiyuanhao1998/BiSCI
代码链接：https://github.com/caiyuanhao1998/MST
（1）提出了光谱压缩重建领域内首个基于二值神经网络（Binarized Neural Network，BNN）的算法 — 二值化光谱重分布网络（Binarized Spectral-Redistribution Network，BiSRNet）；
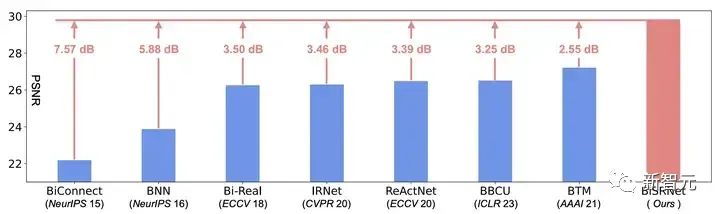图3 BiSRNet 与当前最先进的二值网络的性能对比
（2）设计了一个新的二值化卷积单元 — 二值化光谱重分布卷积（Binarized Spectral-Redistribution Convolution，BiSR-Conv）。该卷积单元可以调整光谱表征的强度和分布，同时在反向传播中更好地逼近二值化符号（Sign）函数，从而让求得的梯度更加准确；
（3）制作了四个二值化卷积模块来解决特征图形变过程中的维度不匹配问题，从而让全精度信息能流通整个模型的每一层卷积单元以弥补二值卷积造成的信息损失；
（4）我们的 BiSRNet 显著地超越了当前最先进的二值化算法，甚至取得了能与全精度CNN比肩的效果，然而我们的BiSRNet算法却只需要极低的存储空间（约 0.06 %）和计算代价（约 1%）。
目前所有的代码，预训练模型和测试结果均已开源在一个二值化光谱压缩重建工具包 BiSCI 内，该工具包支持八类最主要的二值网络，欢迎大家来使用。
同时，我们还将 BiSRNet 嵌入到了我们之前开发的光谱重建工具箱 MST 当中。目前 MST 工具包已支持超过 12 类深度学习算法，并包含各种配套的可视化函数，欢迎大家来对比。
方法介绍
基础模型
一般来说，用于二值化的全精度模型应该是比较轻量的且它的计算单元可以再移动端设备上运行。然而，现存的CNN 或 Transformer 模型均不满足这一要求。为此，我们重新设计了一个简单，轻量，易于部署的基础模型（Base Model）。
受到之前工作 MST，MST++，CST，DAUHST 的启发，我们设计的基础模型也采用一个 U 形结构，如图4所示。
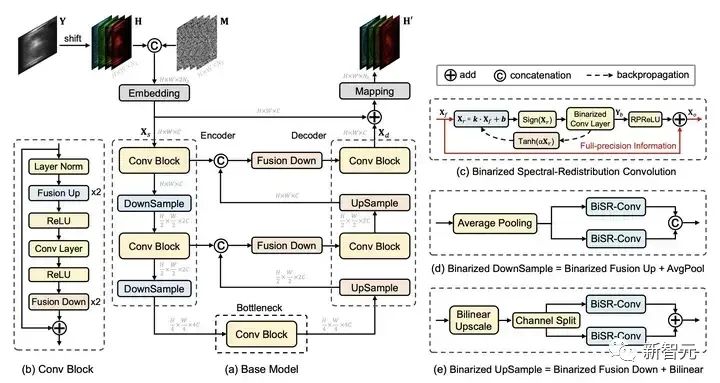图4 基础模型的网络结构
在这个基础模型中，采用的所有计算单元都可以被移动端设备支持，同时也不涉及计算复杂度高的操作。
二值化光谱重分布卷积单元
二值化光谱重分布卷积的细节如图 4（c）所示。将输入的全精度激活信号记为Xf，可以注意到，受到特定成像波长的限制，高光谱信号沿着光谱维度有着不同的强度与分布。
为了适应光谱图像的这一特性，我们提议在二值化激活之前，按通道对高光谱图像表示进行重分布：
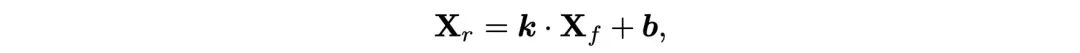图片
其中的Xr表示重分布后的激活，k和b表示可学习参数，然后Xr经过一个符号函数后被量化到1位的激活Xb：
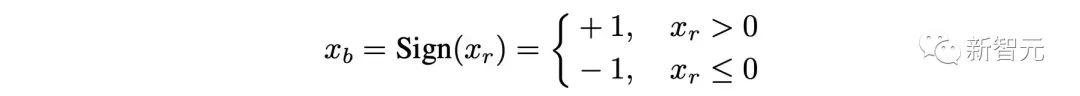图片
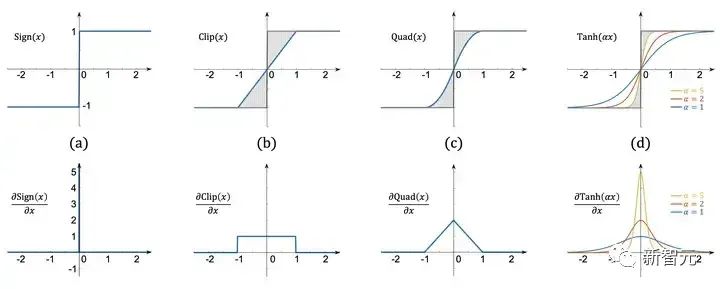
如图 5 (b) 和 (c) 所示，由于符号函数是不可导的，之前的方法大都采用一个分段线性函数 Clip(x) 或者二次函数 Quad(x) 来在反向传播中拟合符号函数。
图片
图 5 符号函数与各类逼近函数的对比图
Clip(x) 与 Quad(x) 的具体表达式如下：
图片
然而分段线性函数知识一个粗略的估计，它与符号函数之间依旧有着很大的误差。
图 5 中的阴影部分面积就表示这个误差的大小，Clip(x) 的误差是1。此外，一旦激活或者权重的值落在了 [-1, 1] 之外，他们就不会再被更新。
尽管分段二次函数是一个更精确的逼近（误差为2/3），上述的两个问题依旧存在。
为此，我们设计了一个可缩放的双曲正切函数来在反向传播中拟合符号函数：
图片
其中α>0 是一个可学习的参数，自适应地调整 Tanh(αx) 与 Sign(x) 之间的距离。
我们证明当 α→+∞ 时，Tanh(αx)→Sign(x)如下：
图片
我们仿照之前的二值化算法，定义：
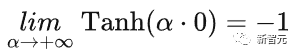图片
然后可以得到：
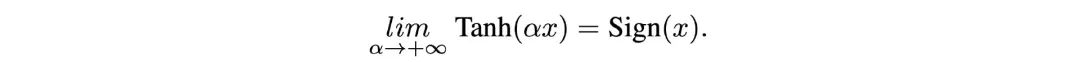图片
然后计算图 5 (d) 中的阴影面积：
图片
由此可见，当α足够大时，Tanh(αx)可以任意地逼近 Sign(x)，同时，我们的 Tanh(x) 既不是分段函数，也不会因为 x 落在 [-1, 1] 之外而无法更新。
更进一步，我们比较三个逼近函数的一阶导数，如图 5 下边一行所示， ∂Clip(x)/∂x与∂Quad(x)∂x的取值范围均为 [0,1]，这与 ∂Sign(x)∂x∈[0,+∞) 有着本质的区别。
而我们的 ∂Tanh(αx)∂x 可以通过改变参数α来调整它的取值范围 (0, α) 和形状，从而更加灵活地逼近 ∂Sign(x)∂x
在二值化卷积层当中，32位的权重Wf也被二值化到一位的权重Wb：
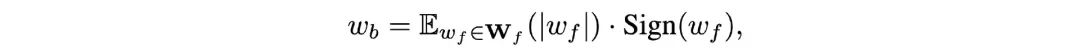图片
其中的E表示取均值。由此，计算繁重的全精度卷积操作便可由纯逻辑异或非运算（XNOR）与位计数（bit-count）操作替换如下：
图片
因为全精度信息Xf的取值范围与二值卷积的输出Yb差别较大，直接引入残差连接将两者相加容易导致 Yb的信息被淹没掉，所以先采用一个 RPReLU 激活函数来重塑Yb的取值范围：
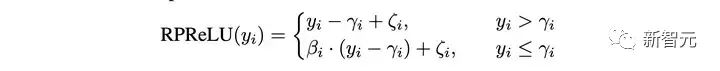图片
然后再引入残差链接：
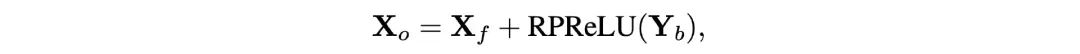图片
通过我们的设计，全精度信息流就不会被二值卷积给阻断，从而能够顺畅地流过我们设计的 BiSR-Conv 单元，如图 4 (c) 中的红色箭头所示。
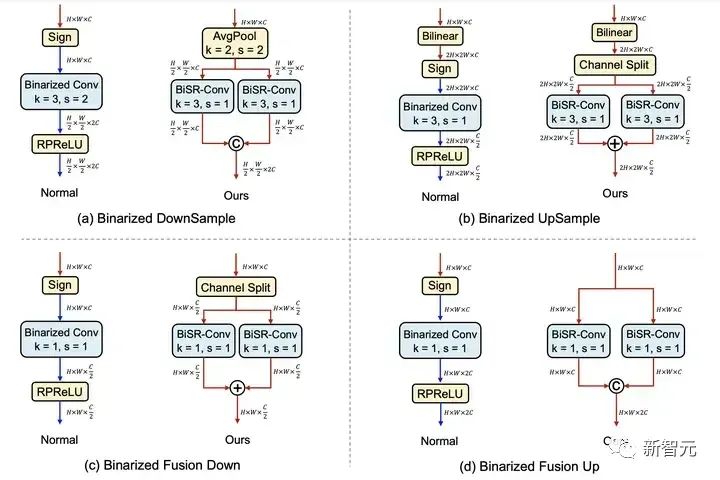图片
图6 本文卷积二值卷积块与普通二值卷积块在处理特征图维度变化时的对比
全精度信息流在二值化算法中非常重要，因为它在一定程度上弥补了量化导致的信息损失。然而在特征图的上下采样过程中，由于维度发生了变化，难以直接引入残差链接以补充全精度信息，如图 6 中每个子图的左半部分所示。
蓝色箭头表示二值信号，红色箭头表示全精度信息流。普通的二值卷积模块会在特征度维度改变的同时阻断全精度信息流的传递。然而我们的二值卷积模块通过采用分割合并的技巧，让全精度信息流不被阻断，从而在整个二值模型中流通。
实验结果
量化指标
表1 BiSRNet 与 SOTA BNN，传统方法，全精度CNN方法的量化指标对比
表 1 展示了我们的 BiSRNet 与 SOTA BNN，传统方法，全精度 CNN 方法的量化指标对比。可以看到，我们的 BiSRNet 显著超越了当前最先进的 BNN 算法 BTM 2.55 dB。
同时超越了所有的 64 位传统算法，增幅超过了4.49dB，值得注意的是，我们的 BiSRNet 取得了能与全精度 CNN 方法比肩的性能，比如超过了 λ−Net 1.23 dB，然而却只占用了 0.06 % 的存储空间和 1 % 计算代价。
视觉对比
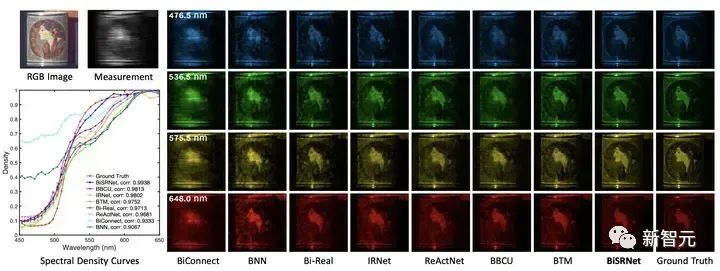图7 BiSRNet 与其他 BNN 方法在仿真数据及上的视觉对比
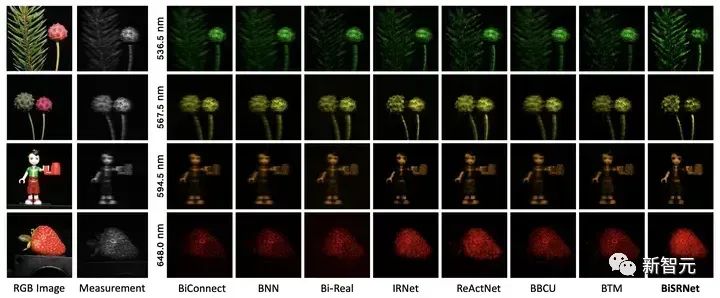图8 BiSRNet 与其他 BNN 方法在真实数据集上的视觉对比
参考资料：
