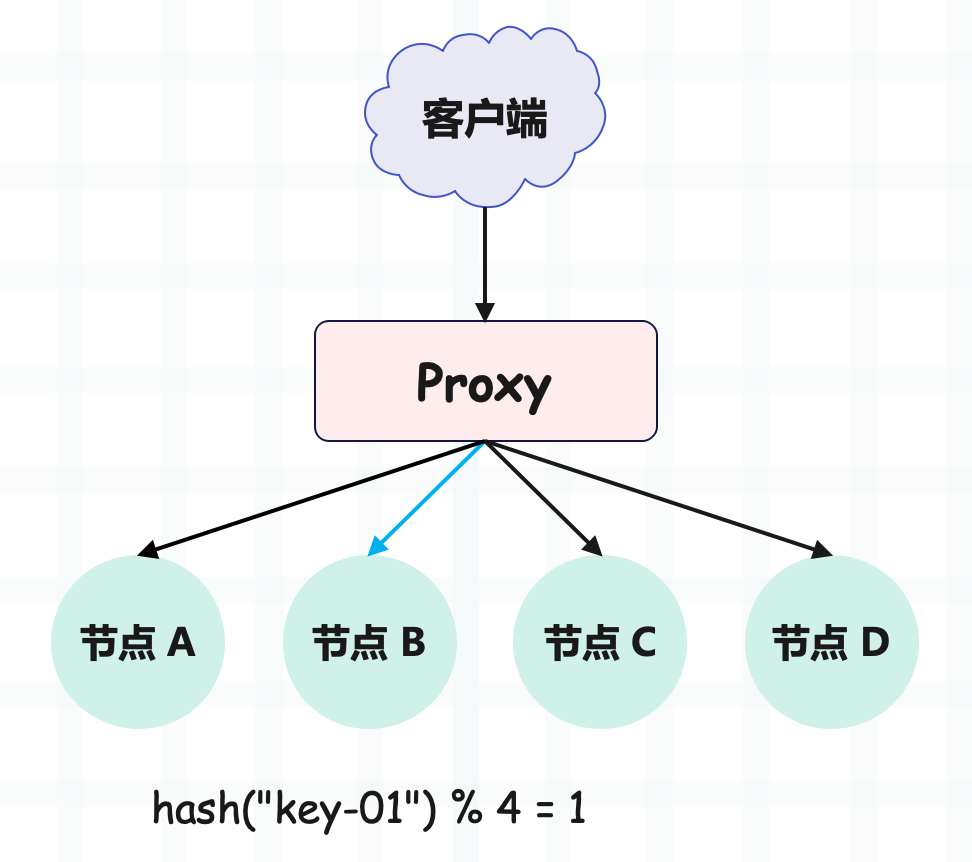
为了提升数据的读写速度,我们一般会引入缓存,如果数据量很大,一个节点的缓存容纳不下,那么就会采用多节点,也就是分布式缓存。具体做法是在节点前面加一个 Proxy 层,由 Proxy 层统一接收来自客户端的读写请求,然后将请求转发给某个节点。
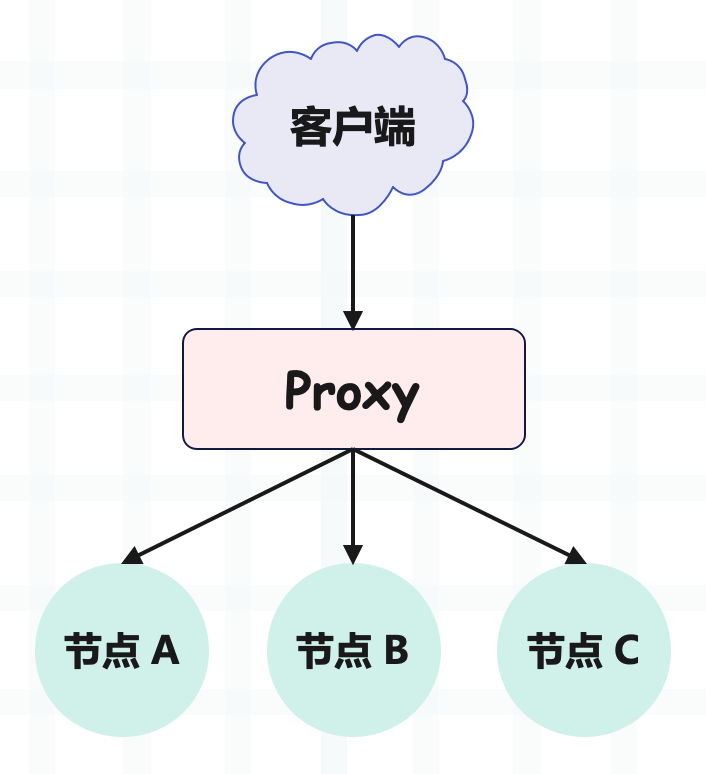
但这就产生了一个问题,既然有多个节点(比如上图有 A、B、C 三个节点,每个节点存放不同的 KV 数据),那么写数据的时候应该写到哪一个节点呢?读数据,又应该从哪一个节点去读呢?
维度考量
对于任何一个分布式存储系统,在存储数据时,我们通常都会从数据均匀、数据稳定和节点异构性这三个维度来考量。
数据均匀
不同节点中存储的数据要尽量均匀,不能因数据倾斜导致某些节点存储压力过大,而其它节点却几乎没什么数据。比如有 4 个相同配置的节点要存储 100G 的数据,那么理想状态就是让每个节点存储 25G 的数据。
此外用户访问也要做到均匀,避免出现某些节点的访问量很大,但其它节点却无人问津的情况。比如要处理 1000 个请求,理想状态就是让每个节点处理 250 个请求。
当然这是非常理想的情况,实际情况下,只要每个节点之间相差不太大即可。
数据稳定
当存储节点出现故障需要移除、或者需要新增节点时,数据按照分布规则得到的结果应该尽量保持稳定,不要出现大范围的数据迁移。
比如 4 个节点存储 100G 数据,但现在其中一个节点挂掉了,那么只需要将挂掉的节点存储的数据迁移到其它正常节点即可,而不需要大范围对所有数据进行迁移。当然新增节点也是同理,要在尽可能小的范围内将数据迁移到扩展的节点上。
节点异构性
不同存储节点的硬件配置可能差别很大,配置高的节点能存储的数据量、单位时间处理的请求数,本身就高于配置低的节点。
如果这种硬件配置差别很大的节点,存储的数据量、处理的请求数都差不多,那么反倒不均匀了。所以,一个好的数据分布算法应该考虑节点异构性。
当然,除了上面这 3 个维度外,我们一般还会考虑隔离故障域、性能稳定性等因素。
隔离故障域
用于保证数据的可用性和可靠性,比如我们通常通过备份来实现数据的可靠性。但如果每个数据及它的备份,被分布到了同一块硬盘或节点上,就有点违背备份的初衷了。
所以一个好的数据分布算法,给每个数据映射的存储节点应该尽量在不同的故障域,比如不同机房、不同机架等。
性能稳定性
数据存储和查询的效率要有保证,不能因为节点的添加或者移除,造成读写性能的严重下降。
了解完数据分布的设计原则后,再来看看主流的数据分布式方法,也就是哈希算法,以及基于哈希算法演进出的一些算法。
哈希
通过对 key 进行哈希,然后再用哈希值对节点个数取模,即可寻址到对应的服务器。
比如查询名为 key-01 的 key,计算公式是 hash("key-01") % 3 ,经过计算寻址到了编号为 0 的服务器节点 A,如下图所示。
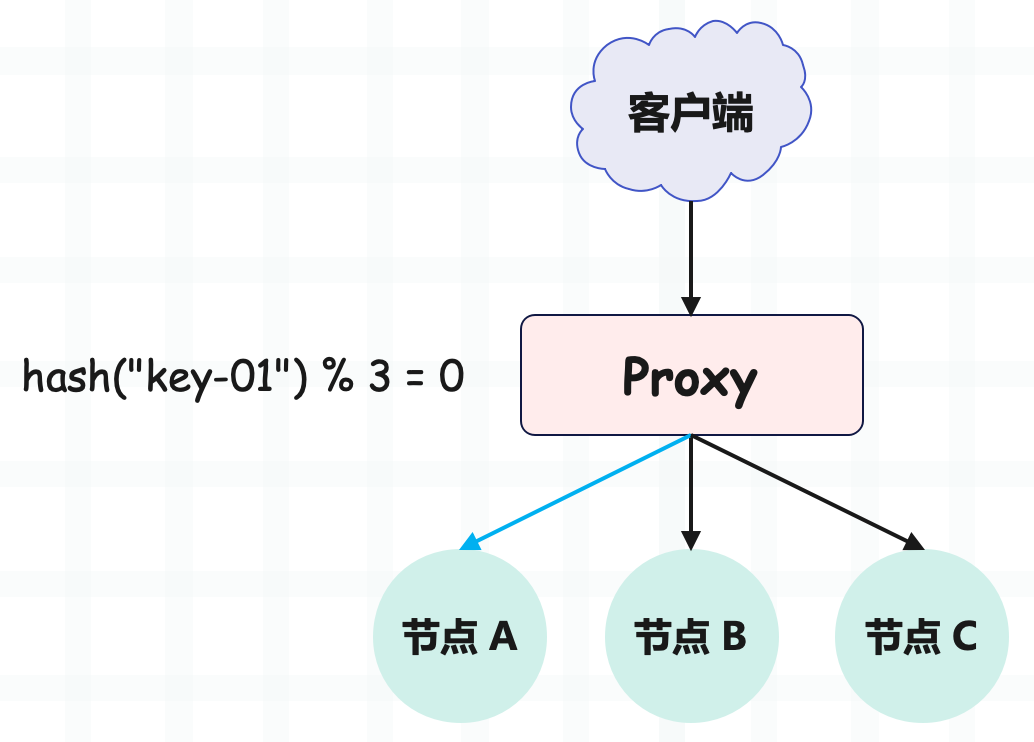
不难发现,哈希算法非常简单直观,如果选择一个好的哈希函数,是可以让数据均匀分布的。但哈希算法有一个致命的缺点,就是它无法满足节点动态变化。比如节点数量发生变化,基于新的节点数量来执行哈希算法的时候,就会出现路由寻址失败的情况,Proxy 无法寻址到之前的服务器节点。
想象一下,假如 3 个节点不能满足业务需要了,我们增加了一个节点,节点的数量从 3 变成 4。那么之前的 hash("key-01") % 3 = 0,就变成了 hash("key-01") % 4 = X。
因为取模运算发生了变化,所以这个 X 大概率不是 0(假设 X 为 1),这时再查询,就会找不到数据了。因为 key-01 对应的数据,存储在节点 A 上,而不是节点 B。
同样的道理,如果我们需要下线 1 个服务器节点,也会存在类似的可能查询不到数据的问题。
而解决这个问题的办法在于我们要迁移数据,基于新的计算公式 hash("key-01") % 4,来重新对数据和节点做映射。但需要注意的是,数据的迁移成本是非常高的,对于 3 节点 KV 存储,如果我们增加 1 个节点,变为 4 节点集群,则需要迁移 75% 的数据。
所以哈希算法适用于节点配置相同,并且节点数量固定的场景。如果节点会动态变化,那么应该选择一致性哈希算法。
 一致性哈希
一致性哈希
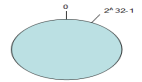
一致性哈希也是基于哈希实现的,哈希算法是对节点的数量进行取模运算,而一致性哈希算法是对 2^32 进行取模运算。想象一下,一致性哈希算法将整个哈希值空间组织成一个虚拟的圆环,也就是哈希环:
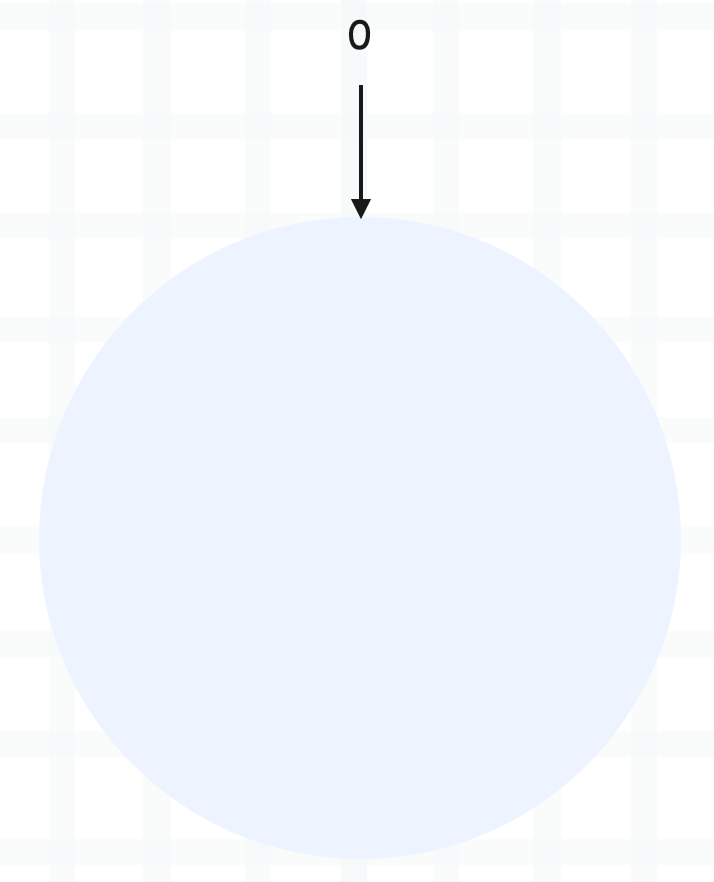
哈希环的空间按顺时针方向组织,圆环的正上方的点代表 0,0 右侧的第一个点代表 1,以此类推,2、3、4、5、6……直到 2^32-1。
在一致性哈希中,你可以通过执行哈希算法,将节点映射到哈希环上。比如选择节点的主机名作为参数执行哈希再取模,那么就能确定每个节点在哈希环上的位置了。
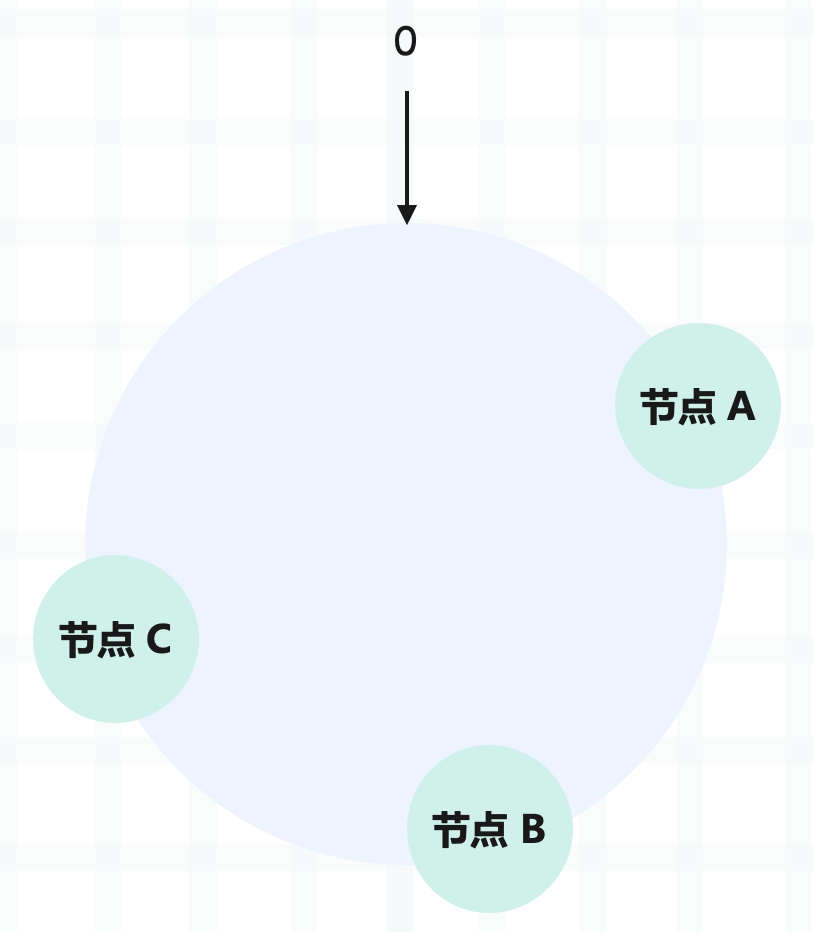
当需要对指定 key 的值进行读写的时候,可以通过下面两步进行寻址:
- 首先,对 key 进行哈希再取模,并确定此 key 在环上的位置。
- 然后,从该位置沿着哈希环顺时针行走,遇到的第一个节点就是 key 对应的节点。
我们举个例子,假设 key-01、key-02、key-03 三个 key,经过哈希取模后,在哈希环中的位置如下:
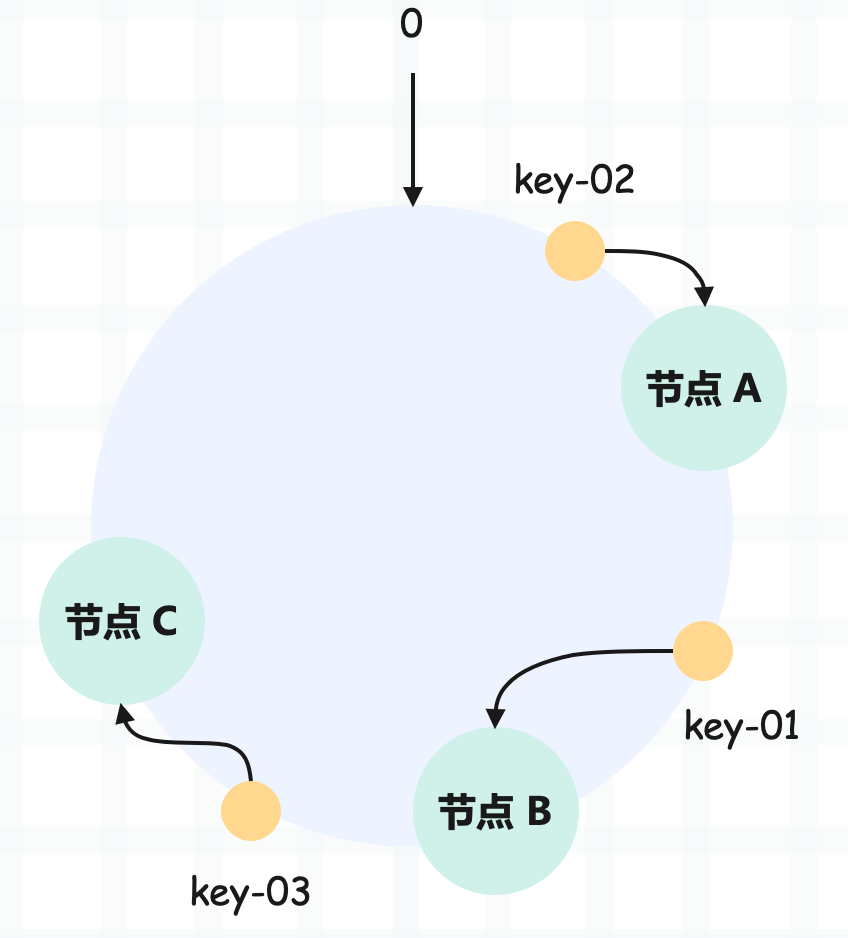
根据一致性哈希算法,key-01 寻址到节点 B,key-02 寻址到节点 A,key-03 寻址到节点 C。如果只考虑数据分布的话,那么一致性哈希算法和哈希算法差别不太大,但一致性哈希解决了节点变化带来的数据迁移问题。
假设,现在有一个节点故障了(比如节点 C):
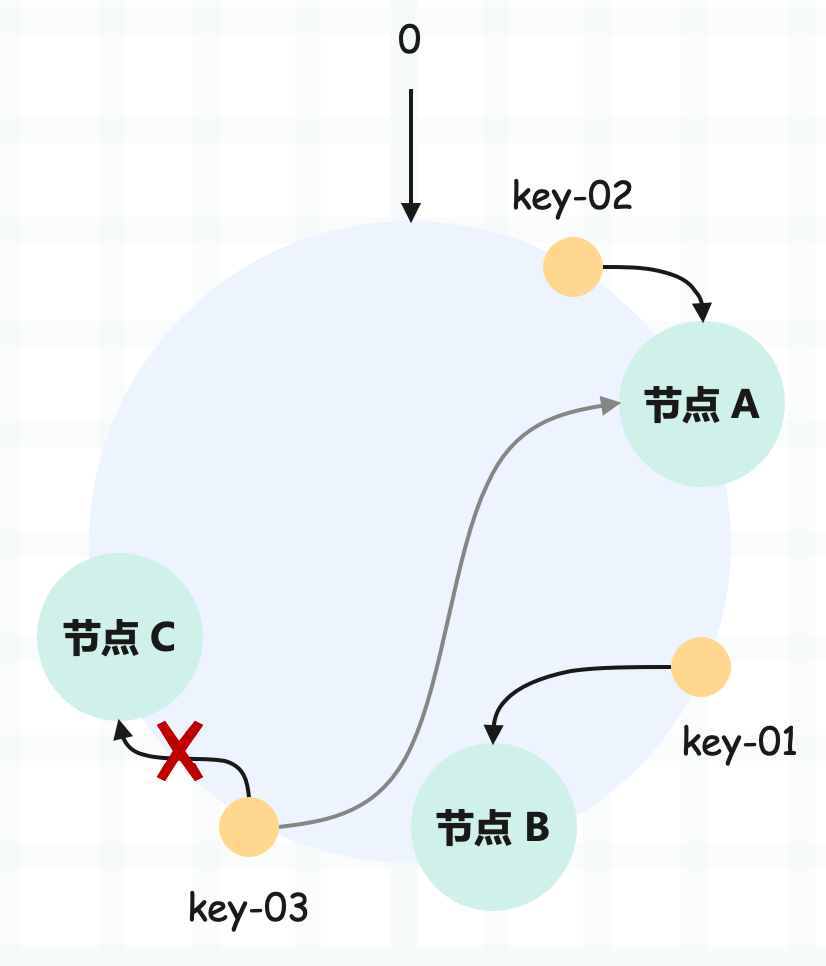
可以看到,key-01 和 key-02 不会受到影响,只有 key-03 的寻址被重定位到 A。一般来说,在一致性哈希算法中,如果某个节点宕机不可用了,那么受影响的数据仅仅是故障节点和前一节点之间的数据。
比如当节点 C 宕机了,受影响的数据是节点 B 和节点 C 之间的数据(例如 key-03),寻址到其它哈希环空间的数据(例如 key-01),不会受到影响。
如果此时集群不能满足业务的需求,需要扩容一个节点 D 呢?
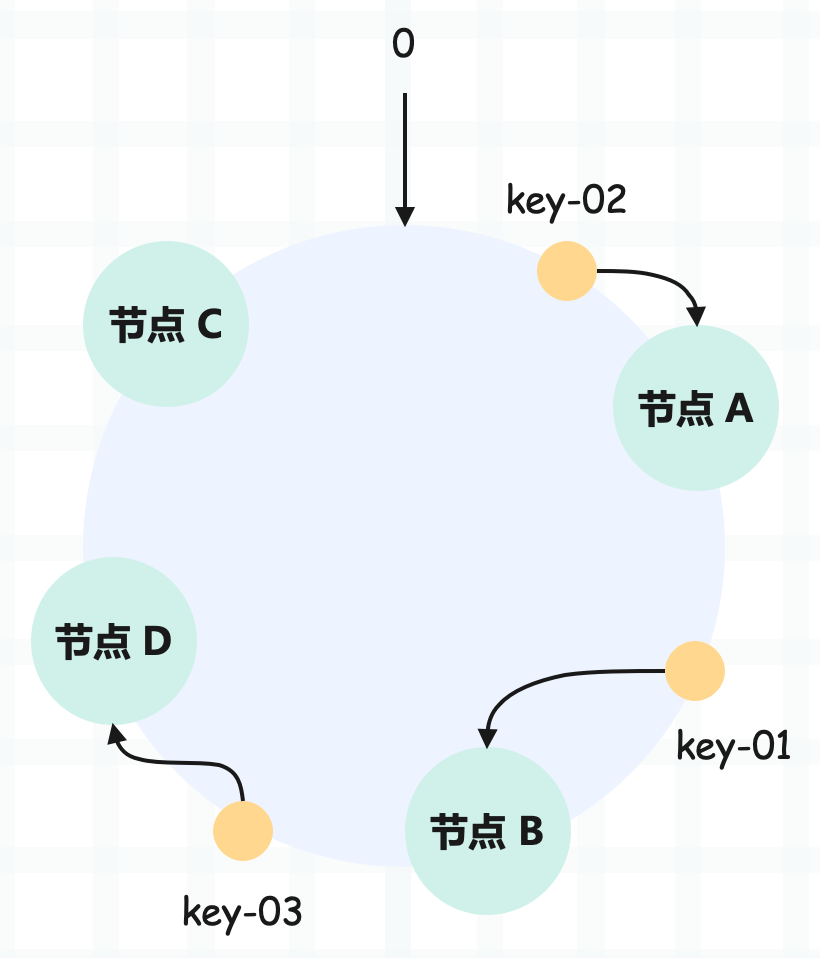
可以看到 key-01、key-02 不受影响,只有 key-03 的寻址被重定位到新节点 D。一般而言,在一致性哈希算法中,如果增加一个节点,受影响的数据仅仅是新节点和前一节点之间的数据,其它数据也不会受到影响。
使用一致性哈希的话,对于 3 节点 KV 存储,如果我们增加 1 个节点,变为 4 节点集群,则只需要迁移 24.3% 的数据。迁移的数据量仅为使用哈希算法时的三分之一,从而大大提升效率。
总的来说,使用了一致性哈希算法后,扩容或缩容的时候,都只需要重定位环空间中的一小部分数据。所以一致性哈希算法是对哈希算法的改进,在采用哈希方式确定数据存储位置的基础上,又增加了一层哈希,也就是在数据存储前先对存储节点进行哈希,具有较好的容错性和可扩展性。
一致性哈希比较适合节点配置相同、但规模会发生变化的场景。
我们用 Python 简单实现一下一致性哈希:
from typing import Union, List
import hashlib
import bisect
class ConsistentHash:
def __init__(self,
nodes: List[str] = None,
ring_max_len=2 ** 32):
# 哈希环的最大长度
self.ring_max_len = ring_max_len
# 节点在哈希环上的索引(有序)
self.node_indexes = []
# '节点在哈希环上的索引' 到 '节点' 的映射
self.nodes_mapping = {}
if nodes:
for node in nodes:
self.add_node(node)
def get_index(self, item: Union[str, bytes]):
"""
获取节点或者 key 在哈希环上的索引
"""
if type(item) is str:
item = item.encode("utf-8")
md5 = hashlib.md5()
md5.update(item)
# md5.hexdigest() 会返回 16 进制字符串,将其转成整数
# 然后是取模,如果 n 是 2 的幂次方,那么 m % n 等价于 m & (n - 1)
# 所以字典的容量一般都是 2 的幂次方,就是为了将取模优化成按位与
return int(md5.hexdigest(), 16) & (self.ring_max_len - 1)
def add_node(self, node):
"""
node 可以是节点的信息,比如一个字典
但这里为了方便,node 就表示节点名称
"""
node_index = self.get_index(node)
# 节点索引是有序的,新增时使用 bisect 可将复杂度优化为 logN
bisect.insort(self.node_indexes, node_index)
self.nodes_mapping[node_index] = node
print(f"节点 {node} 被添加至哈希环, 索引为 {node_index}")
def remove_node(self, node):
# 移除节点
node_index = self.get_index(node)
self.node_indexes.remove(node_index)
self.nodes_mapping.pop(node_index)
print(f"节点 {node} 从哈希环中被移除")
def get_node(self, key):
"""
判断 key 应该被存在哪一个 node 中
"""
key_index = self.get_index(key)
# node_indexes 里面存储了所有节点在哈希环的索引
# 所以只需要遍历即可
for node_index in self.node_indexes:
if node_index >= key_index:
break
else:
node_index = self.node_indexes[0]
# 如果节点索引大于等于 key 的索引,那么就找到了指定节点
# 如果遍历结束还没有找到,说明 key 的索引大于最后一个节点的索引
# 这样的话,该 key 应该存在第一个节点
node = self.nodes_mapping[node_index]
# todo:连接指定节点,存储 key 和 value
print(f"key `{key}` 存在了节点 `{node}` 上")
ch = ConsistentHash(nodes=["node1", "node2", "node3"])
"""
节点 node1 被添加至哈希环, 索引为 2595155078
节点 node2 被添加至哈希环, 索引为 3803043663
节点 node3 被添加至哈希环, 索引为 385180855
"""
ch.get_node("S 老师四点下班")
ch.get_node("高老师总能分享出好东西")
ch.get_node("电烤🐔架")
"""
key `S 老师四点下班` 存在了节点 `node3` 上
key `高老师总能分享出好东西` 存在了节点 `node1` 上
key `电烤🐔架` 存在了节点 `node1` 上
"""
# 删除节点
ch.remove_node("node3")
"""
节点 node3 从哈希环中被移除
"""
# 当节点被删除后,存储位置发生变化
ch.get_node("S 老师四点下班")
"""
key `S 老师四点下班` 存在了节点 `node1` 上
"""当然啦,在节点被移除时,应该自动进行数据迁移。这里就不实现了,有兴趣的话可以尝试一下。
然后一致性哈希也有它的一些问题,比如读写可能集中在少数的节点上,导致有些节点高负载,有些节点低负载的情况。
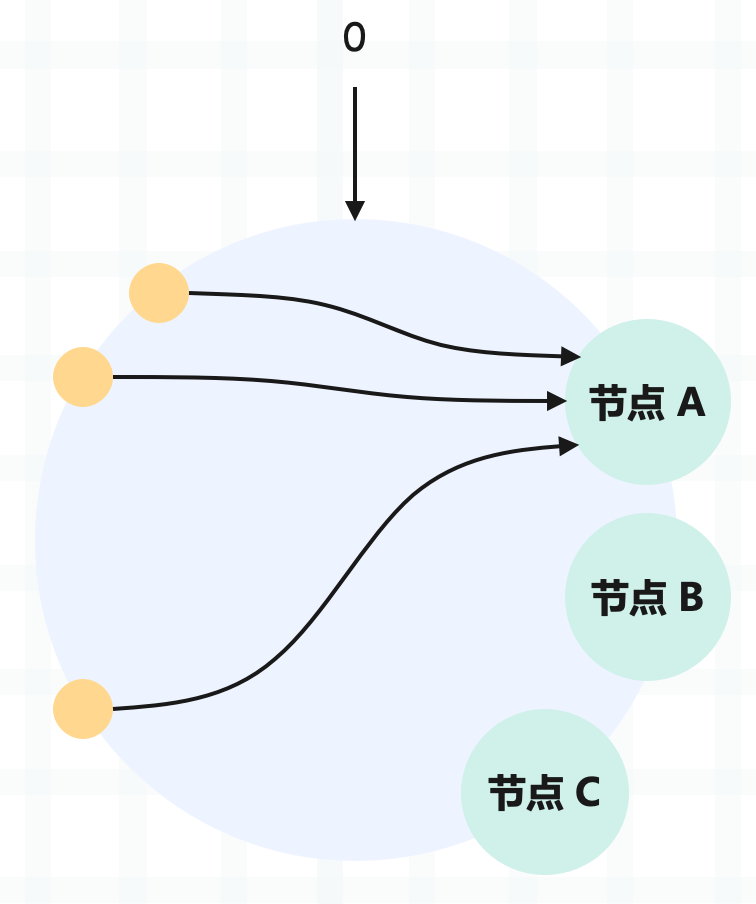
从图中可以看到,虽然有 3 个节点,但访问请求主要集中在节点 A 上。当然这个问题其实不大,我们可以设计一个好的哈希函数,让节点均匀分布。
但一致性哈希还存在击垮后继节点的风险,如果某个节点退出,那么该节点的后继节点需要承担该节点的所有负载。如果后继节点承受不住,那么也可能出现故障,从而导致后继节点的后继节点也面临同样的问题,引发恶性循环。
那么如何解决后继节点可能被压垮的问题呢?针对这个问题,Google 提出了带有限负载的一致性哈希算法。
带有限负载的一致性哈希
带有限负载的一致性哈希的核心原理是,给每个存储节点设置一个存储上限值,来控制存储节点添加或移除造成的数据不均匀。
当数据按照一致性哈希算法找到相应的节点时,要先判断该节点是否达到了存储上限。如果已经达到了上限,则需要继续寻找该节点顺时针方向之后的节点进行存储。
所以该算法相当于在一致性哈希的基础上,给节点增加了一些存储上限,它的适用场景和一致性哈希是一样的。目前在 Google、Vimeo 等公司的负载均衡项目中得到应用。
当然啦,无论是哈希、一致性哈希,还是带有限负载的一致性哈希,它们的适用场景都要求节点的配置相同,换句话说就是没有考虑节点异构性的问题。如果存储节点的硬件配置不同,那么采用上面算法实现的数据均匀分布,反倒变得不均匀了。
所以便引入了虚拟节点。
带虚拟节点的一致性哈希
带虚拟节点的一致性哈希,核心思想是根据每个节点的性能,为每个节点划分不同数量的虚拟节点,并将这些虚拟节点映射到哈希环中,然后再按照一致性哈希算法进行数据映射和存储。
比如三个节点 A、B、C,以节点 C 为基准,节点 B 的性能是它的 2 倍,节点 A 是它的 3 倍。因此要给节点 C 添加 1 个虚拟节点,给节点 B 添加 2 个虚拟节点,给节点 A 添加 3 个虚拟节点。
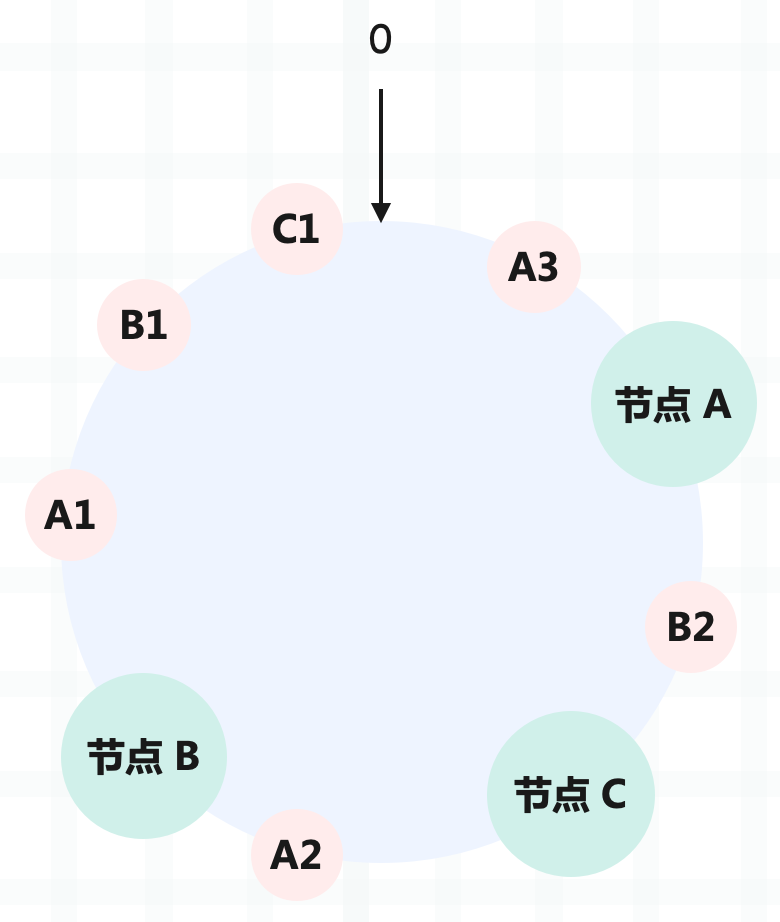
节点 A 的虚拟节点是 A1、A2、A3,节点 B 的虚拟机节点是 B1、B2,节点 C 的虚拟节点是 C1。当然虚拟节点的数量不一定是 1、2、3,也可以按照比例进行增加。
总之通过增加虚拟节点,可以考虑到节点异构性,让性能高的节点多分配一些请求。
如果节点配置一样,也可以使用该算法,只不过此时每个节点对应的虚拟节点是一样的。并且采用这种方式,可以有效避免节点倾斜的问题,不会出现大部分请求都打在同一节点的情况。
可以看出,带虚拟节点的一致性哈希比较适合异构节点、节点规模会发生变化的场景。
这种方法不仅解决了节点异构性问题,还提高了系统的稳定性。当节点变化时,会有多个节点共同分担系统的变化,因此稳定性更高。
比如当某个节点被移除时,对应该节点的多个虚拟节点均会被移除。而这些虚拟节点按顺时针方向的下一个虚拟节点,可能会对应不同的物理节点,即这些不同的物理节点共同分担了节点变化导致的压力。
Memcached 便实现了该方法。
当然,由于引入了虚拟节点,增加了节点规模,从而增加了节点的维护和管理的复杂度。比如新增一个节点或一个节点故障时,对应到哈希环上则需要新增和删除多个节点,数据的迁移等操作也会相应的变复杂。
 小结
小结
一致性哈希是一种特殊的哈希算法,在使用一致性哈希算法后,节点增减变化时只影响到部分数据的路由寻址,也就是说我们只要迁移部分数据,就能实现集群的稳定了。
当某个节点退出时,会有压垮后继节点的风险,因此可以给每个节点设置一个上限。如果所有节点都达到了上限怎么办?说明你需要调整上限或增加节点了。
当节点数较少时,可能会出现节点在哈希环上分布不均匀的情况,这样每个节点实际占据环上的区间大小不一,最终导致业务对节点的访问冷热不均。此时我们可以通过引入更多的虚拟节点来解决这个问题,当然通过虚拟节点也可以解决节点异构性的问题。
总之节点数越多,使用哈希算法时,需要迁移的数据就越多;使用一致性哈希时,需要迁移的数据就越少。经过测试,当我们向 10 个节点组成的集群中增加节点时,如果使用了哈希算法,需要迁移高达 90.91% 的数据,使用一致性哈希的话,则只需要迁移 6.48% 的数据。