Transformer 架构可以说是近期深度学习领域许多成功案例背后的主力军。构建深度 Transformer 架构的一种简单方法是将多个相同的 Transformer 「块」(block)依次堆叠起来,但每个「块」都比较复杂,由许多不同的组件组成,需要以特定的排列组合才能实现良好的性能。
自从 2017 年 Transformer 架构诞生以来,研究者们基于其推出了大量衍生研究,但几乎没有改动过 Transformer 「块」。
那么问题来了,标准 Transformer 块是否可以简化?
在最近的一篇论文中,来自 ETH Zurich 的研究者讨论了如何在不影响收敛特性和下游任务性能的情况下简化 LLM 所必需的标准 Transformer 块。基于信号传播理论和经验证据,他们发现可以移除一些部分,比如残差连接、归一化层(LayerNorm)、投影和值参数以及 MLP 序列化子块(有利于并行布局),以简化类似 GPT 的解码器架构以及编码器式 BERT 模型。
对于每个涉及的组件,研究者都探讨了是否可以在不降低训练速度的情况下将其移除(包括每次更新步骤和运行时间),以及为此需要 Transformer 块进行哪些架构修改。

论文链接:https://arxiv.org/pdf/2311.01906.pdf
Lightning AI 创始人、机器学习研究者 Sebastian Raschka 将这项研究称为自己的「年度最爱论文之一」:
但也有研究者质疑:「这很难评,除非我看过完整的训练过程。如果没有归一化层,也没有残差连接,如何能在大于 1 亿参数的网络中进行扩展?」
Sebastian Raschka 表示赞同:「是的,他们试验的架构相对较小,这是否能推广到数十亿参数的 Transformer 上还有待观察。」但他仍然表示这项工作令人印象深刻,并认为成功移除残差连接是完全合理的(考虑到其初始化方案)。
对此,图灵奖得主 Yann LeCun 的评价是:「我们仅仅触及了深度学习架构领域的皮毛。这是一个高维空间,因此体积几乎完全包含在表面中,但我们只触及了表面的一小部分。」

为什么需要简化 Transformer 块?
研究者表示,在不影响训练速度的前提下简化 Transformer 块是一个有趣的研究问题。
首先,现代神经网络架构设计复杂,包含许多组件,而这些不同组件在神经网络训练动态中所扮演的角色,以及它们之间如何相互作用,人们对此尚不清楚。这个问题事关深度学习理论与实践之间存在的差距,因此非常重要。
信号传播理论(Signal propagation)已被证明具有影响力,因为它能够激励深度神经网络架构中的实际设计选择。信号传播研究了初始化时神经网络中几何信息的演化,通过跨输入的分层表征的内积来捕捉,在训练深度神经网络方面取得了许多令人印象深刻的成果。
然而,目前该理论只考虑初始化时的模型,而且往往只考虑初始前向传递,因此无法揭示深度神经网络训练动态的许多复杂问题,例如残差连接对训练速度的助益。虽然信号传播对修改动机至关重要,但研究者表示,他们不能仅从理论上就得出简化的 Transformer 模块,还要依靠经验见解。
在实际应用方面,考虑到目前训练和部署大型 Transformer 模型的高昂成本,Transformer 架构的训练和推理流水线的任何效率提升都代表着巨大的潜在节约意义。如果能够通过移除非必要组件来简化 Transformer 模块,既能减少参数数量,又能提高模型的吞吐量。
这篇论文也提到,移除残差连接、值参数、投影参数和序列化子块之后,可以同时做到在训练速度和下游任务性能方面与标准 Transformer 相匹配。最终,研究者将参数量减少了 16%,并观察到训练和推理时间的吞吐量增加了 16%。
如何简化 Transformer 块?
研究者结合信号传播理论和经验观察,介绍了如何从 Pre-LN 模块出发,生成最简单的 Transformer 块(如下图)。
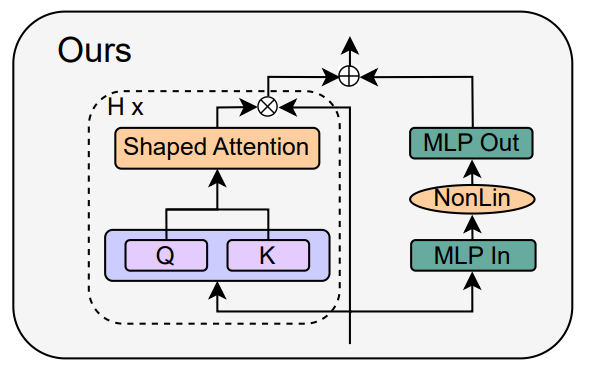
在论文第四章的每一个小节,作者分别介绍了如何在不影响训练速度的情况下每次删除一个块组件。
这一部分的所有实验都在 CodeParrot 数据集上使用了一个 18-block 768-width 的因果仅解码器类 GPT 模型,这个数据集足够大,因此当作者处于单个训练 epoch 模式时,泛化差距非常小(见图 2),这使得他们可以专注于训练速度。
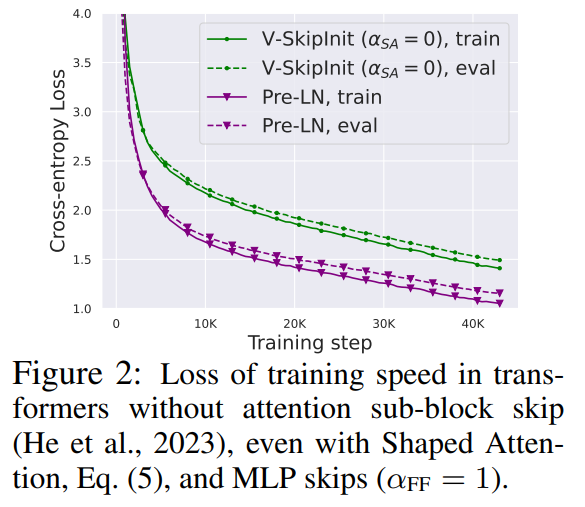
删除残差连接
研究者首先考虑删除注意力子块中的残差连接。在公式(1)的符号中,这相当于将 α_SA 固定为 0。简单地移除注意力残差连接会导致信号退化,即秩崩溃(rank collapse),从而导致可训练性差。在论文 4.1 部分,研究者详细解释了他们的方法。
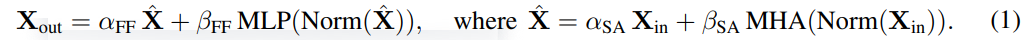
删除投影 / 值参数
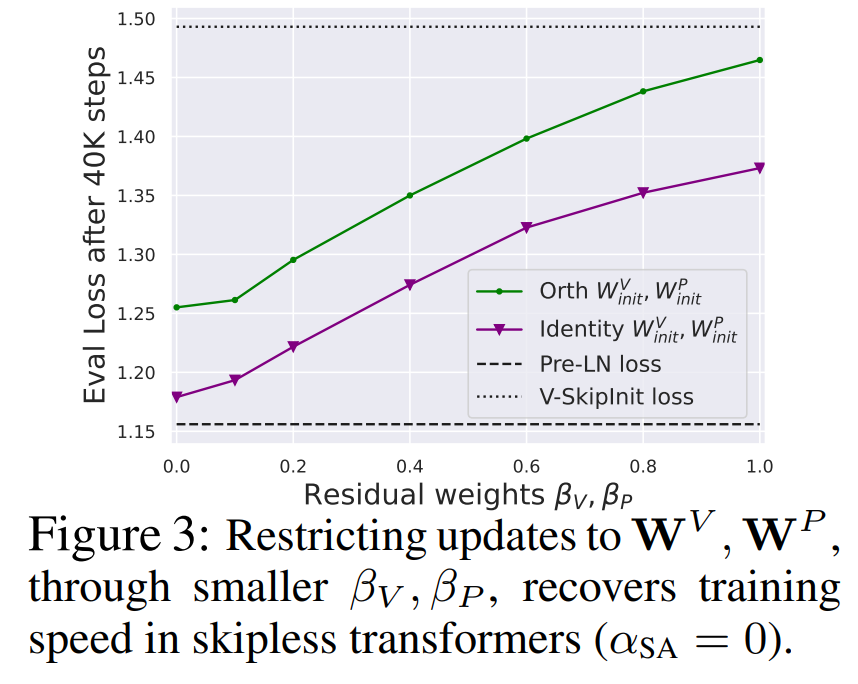
从图 3 中可以得出结论,完全移除值和投影参数 W^V、W^P 是可能的,而且每次更新的训练速度损失最小。也就是说,当 β_V = β_P = 0 和 identity 初始化的
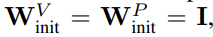
时,在相同的训练步数后,本研究基本上能达到 Pre-LN 块的性能。在这种情况下,在整个训练过程中都有 W^V = W^P = I,即值和投影参数是一致的。作者在 4.2 节介绍了详细方法。
删除 MLP 子块残差连接
与上述几个模块相比,删除 MLP 子块残差连接要更具挑战性。与之前的研究一样,作者发现,在使用 Adam 时,如果没有 MLP 残差连接,通过信号传播使激活更加线性仍会导致每次更新训练速度的显著下降,如图 22 所示。
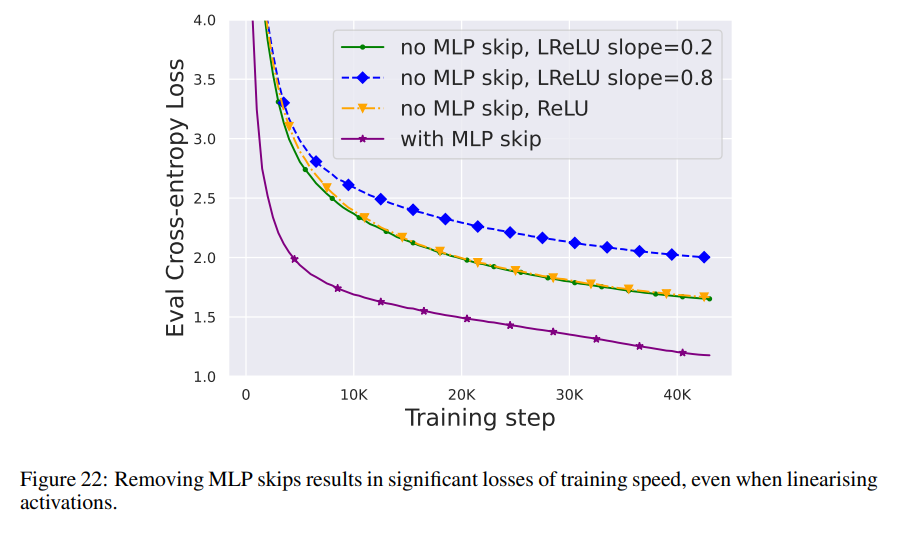
他们还尝试了 Looks Linear 初始化的各种变体,包括高斯权重、正交权重或恒等权重,但都无济于事。因此,他们在整个工作中使用标准激活(例如 ReLU)和 MLP 子块中的初始化。
作者转向并行 MHA 和 MLP 子块的概念,这在几个近期的大型 transformer 模型中已被证明很受欢迎,例如 PALM 和 ViT-22B。并行 transformer 块如下图所示。
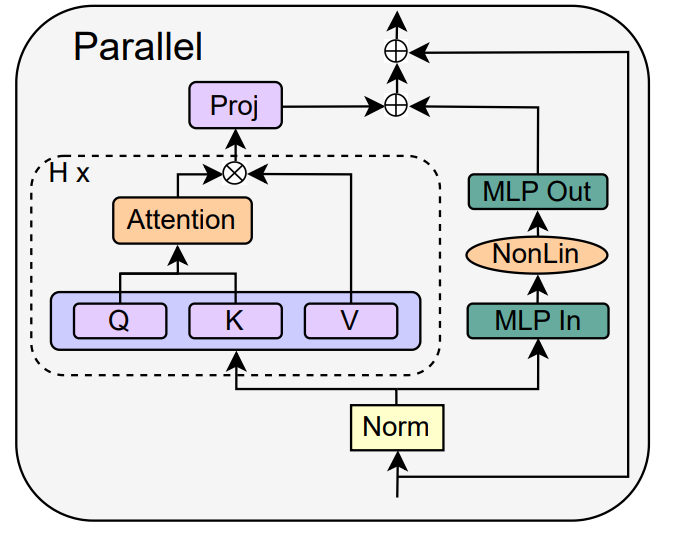
作者在论文 4.3 节详细介绍了移除 MLP 子块残差连接的具体操作。
删除归一化层
最后一个被删除的是归一化层,这样就得到了图 1 右上角的最简块。从信号传播初始化的角度来看,作者可以在本节简化的任何阶段移除归一化层。他们的想法是,Pre-LN 块中的归一化会隐式地降低残差分支的权重,而这种有利的效果可以通过另一种机制在没有归一化层的情况下复制:要么在使用残差连接时明确降低残差分支的权重,要么将注意力矩阵偏向 identity / 将 MLP 非线性转化为「更」线性。
由于作者在修改过程中考虑到了这些机制(如降低 MLP β_FF 和 Shaped Attention 的权重),因此无需进行归一化处理。作者在第 4.4 节介绍了更多信息。
实验结果
深度扩展
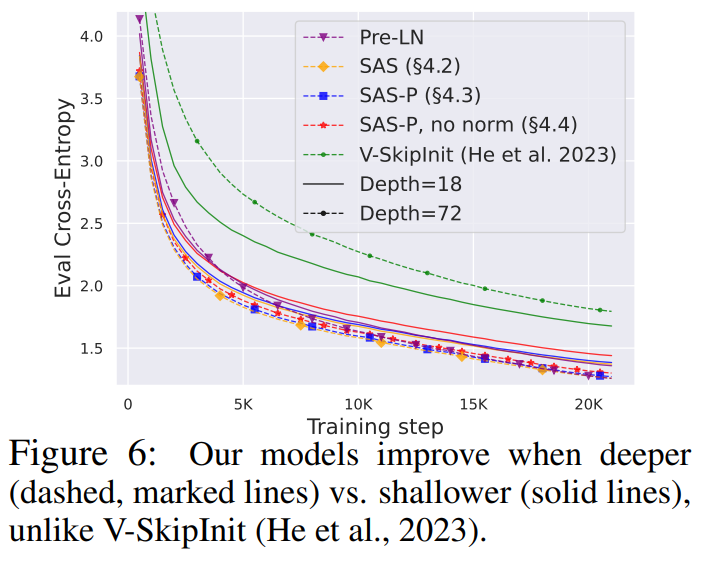
鉴于信号传播理论通常关注很大的深度,而这种情况下通常会出现信号退化。因此一个很自然的问题就是,本文的简化 transformer 块所提高的训练速度是否也能扩展到更大的深度?
从图 6 中可以观察到,将深度从 18 个块扩展到 72 个块后,本研究的模型和 Pre-LN transformer 的性能都得到了提高,这表明本研究中的简化模型不仅训练速度更快,而且还能利用更大的深度所提供的额外能力。事实上,在使用归一化时,本研究中的简化块和 Pre-LN 的每次更新轨迹在不同深度下几乎没有区别。
BERT
接下来,作者展示了他们的简化块性能除了适用于自回归解码器之外,还适用于不同的数据集和架构,以及下游任务。他们选择了双向仅编码器 BERT 模型的流行设置,用于掩蔽语言建模,并采用下游 GLUE 基准。
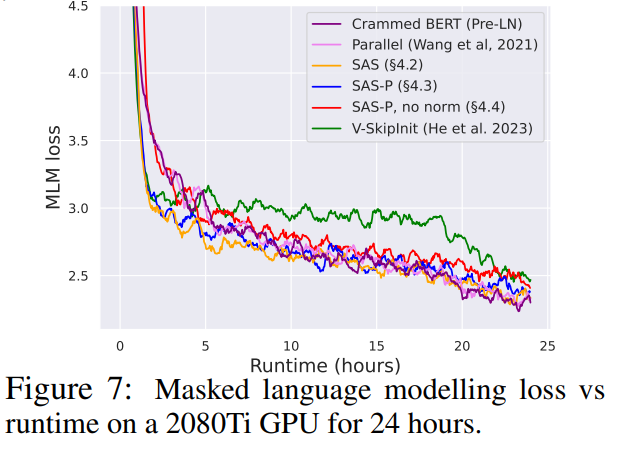
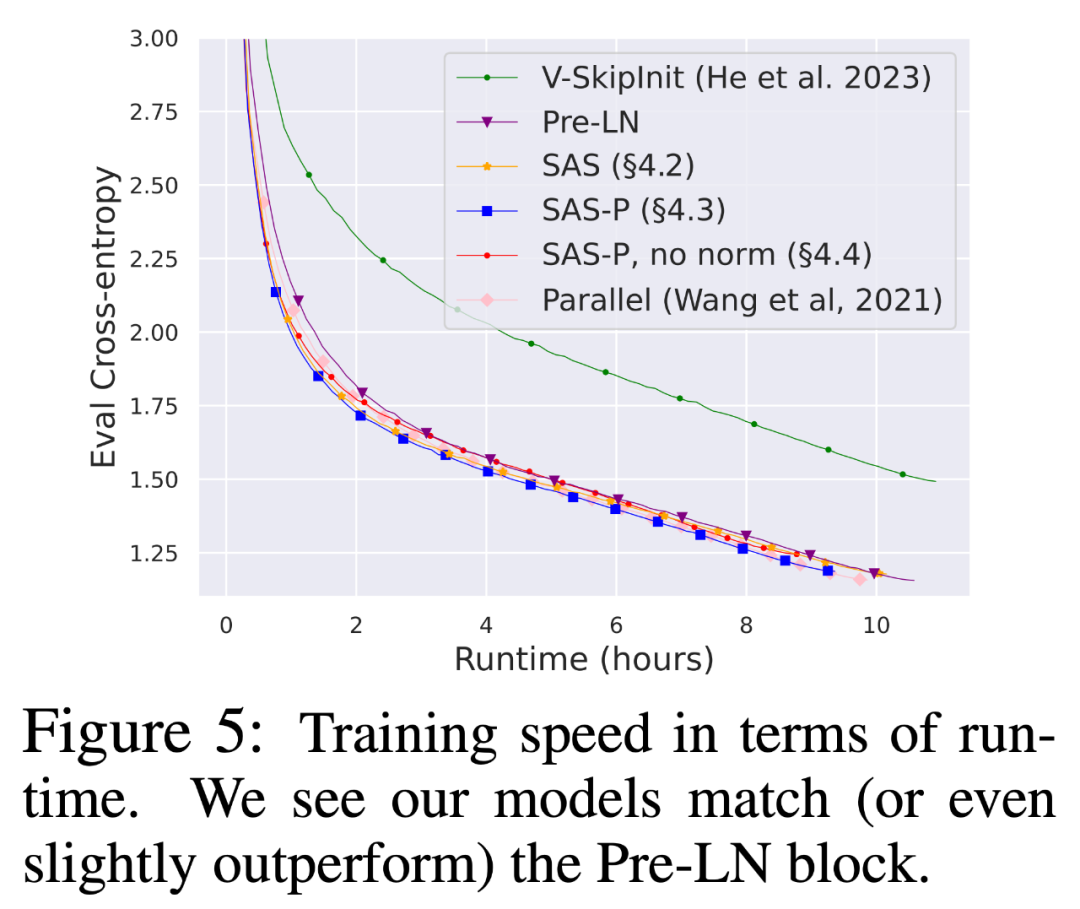
如图 7 所示,在 24 小时运行时内,与(Crammed)Pre-LN 基线相比,本研究的简化块可以媲美掩蔽语言建模任务的预训练速度。另一方面,在不修改值和投影的情况下删除残差连接再次导致训练速度的显著下降。在图 24 中,作者提供了 microbatch 步骤的等效图。
此外,在表 1 中,研究者发现他们的方法在 GLUE 基准上经过微调后,性能与 Crammed BERT 基准相当。
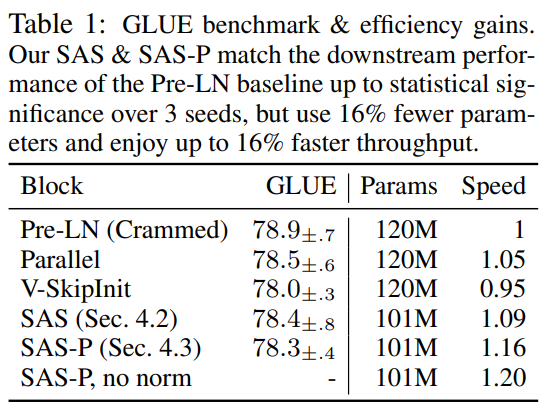
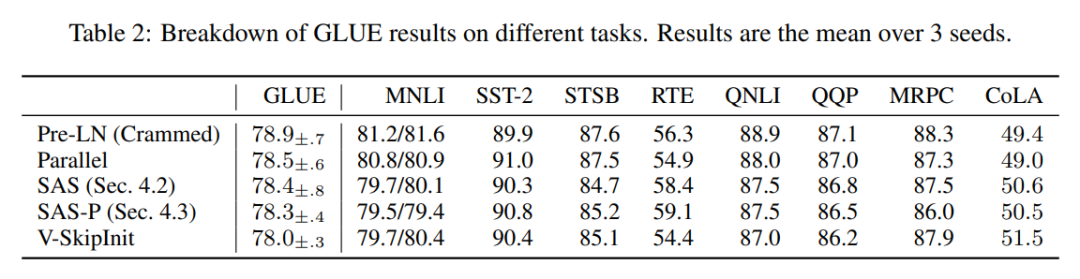
他们在表 2 中对下游任务进行了细分。为了进行公平比较,他们使用了与 Geiping & Goldstein (2023) 相同的微调协议(5 个 epoch、各任务超参数恒定、dropout regularisation)。
效率提升
在表 1 中,研究者还详细列出了使用不同 Transformer 块的模型在掩蔽语言建模任务中的参数数量和训练速度。他们以预训练 24 小时内所采取的 microbatch 步骤数与基线 Pre-LN Crammed BERT 的比率计算了速度。结论是,模型使用的参数减少了 16%,SAS-P 和 SAS 的每次迭代速度分别比 Pre-LN 块快 16% 和 9%。
可以注意到,在这里的实现中,并行块只比 Pre-LN 块快 5%,而 Chowdhery et al.(2022 )观察到的训练速度则快 15%,这表明通过更优化的实现,整个训练速度有可能进一步提高。与 Geiping & Goldstein(2023 年)一样,此处实现也使用了 PyTorch 中的自动算子融合技术 (Sarofeen et al., 2022)。
更长的训练
最后,考虑到当前在更多数据上长时间训练较小模型的趋势,研究者讨论了简化块在长时间训练后是否仍能达到 Pre-LN 块的训练速度。为此,他们在 CodeParrot 上使用图 5 中的模型,并使用 3 倍 token 进行训练。准确地说,是在批大小为 128、序列长度为 128 的情况下进行了约 120K 步(而不是 40K 步)的训练,这将导致约 2B 个 token。
从图 8 可以看出,当使用更多的 token 进行训练时,简化的 SAS 和 SAS-P 代码块的训练速度仍然与 PreLN 代码块相当,甚至优于 PreLN 代码块。
更多研究细节,可参考原论文。































