之前我们总结了机器学习中常用的几种回归算法和分类算法。都属于机器学习监督学习算法。

今天,和大家分享一下机器学习之无监督学习中的常见的降维方法。
我们可以怎样发现一个数据集的底层结构?我们可以怎样最有用地对其进行归纳和分组?我们可以怎样以一种压缩格式有效地表征数据?这都是无监督学习的目标,之所以称之为「无监督」,是因为这是从无标签的数据开始学习的。
降维看上去很像压缩。这是为了在尽可能保存相关的结构的同时降低数据的复杂度。如果你有一张简单的 128×128×3 像素的图像(长×宽×RGB 值),那么数据就有 49152 维。如果你可以给这个图像空间降维,同时又不毁掉图像中太多有意义的内容,那么你就很好地执行了降维。
降维是一种常见的无监督学习任务,其目标是将高维数据映射到低维空间,以减少数据的特征维度,同时保留数据的关键结构和信息。通过降维,可以简化数据表示、减少存储空间、降低计算复杂度,并帮助可视化和数据理解。
降维方法的选择取决于数据的性质、任务需求和算法的适用性。以下是一些常见的降维方法:
- 主成分分析(PCA)
- 独立成分分析(ICA)
算法 t 分布-随机邻近嵌入(t-SNE) 线性判别分析(LDA) - 奇异值分解(SVD)
- 局部线性嵌入(LLE)
- 多维缩放(MDS)
- 等度量映射(Isomap)
1、主成分分析(PCA)
对于降维问题来说,目前最流行最常用的算法是一个叫做主成分分析法(Principal Components Analysis,PCA) 的算法,它可以用来做降维操作,也可以用来实现数据压缩。
PCA 是一种统计分析、简化数据集的方法。它利用正交变换来对一系列可能相关的变量的观测值进行线性变换,从而投影为一系列线性不相关变量的值,这些不相关变量称为主成分(Principal Components)。
具体地,主成分可以看做一个线性方程,其包含一系列线性系数来指示投影方向。PCA 对原始数据的正则化或预处理敏感(相对缩放)。
基本思想
(1)将坐标轴中心移到数据的中心,然后旋转坐标轴,使得数据在 C1 轴上的方差最大,即全部 n 个数据个体在该方向上的投影最为分散。意味着更多的信息被保留下来。C1 成为第一主成分。
(2)C2 第二主成分:找一个 C2,使得 C2 与 C1 的协方差(相关系数)为 0,以免与 C1 信息重叠,并且使数据在该方向的方差尽量最大。
(3)以此类推,找到第三主成分,第四主成分……第 p 个主成分。p 个随机变量可以有 p 个主成分。
主成分分析经常用于减少数据集的维数,同时保留数据集当中对方差贡献最大的特征。这是通过保留低维主成分,忽略高维主成分做到的。这样低维成分往往能够保留住数据的最重要部分。
2、独立成分分析(ICA)算法
独立成分分析(Independent Component Analysis, ICA)算法是一种基于统计学的降维算法,其目的是从多个随机变量的混合信号中恢复出独立的原始信号,即通过对数据进行线性变换,使得变换后的数据各个分量间尽可能地独立。ICA 算法常用于信号处理、图像处理、语音识别、脑电图分析等领域。
ICA 和 PCA 的区别:
(1)PCA 是降维并提取不相关属性,而 ICA 是降维并提取相互独立的属性(不相关不一定独立,独立一定不相关。不相关是指没有线性关系,独立是指没有任何关系)。
(2)PCA 是提取出最能表示原始事物的特征,而 ICA 是使每个分量最大化独立,便于发现隐藏因素
(3)PCA 的适用环境是数据为高斯分布,而 ICA 不适用于高斯分布的数据。
ICA算法的应用
ICA算法在信号处理、图像处理、语音识别等领域有广泛应用。以音频信号处理为例,ICA可以将多个声音信号混合在一起的信号分离开来。在语音识别领域,ICA可以将不同说话人的语音信号分离开来,方便后续的处理。
3、t 分布-随机邻近嵌入(t-SNE)
t-SNE(t-distributed stochastic neighbor embedding)算法是一种非线性降维算法,可以用于高维数据的可视化和聚类分析。t-SNE 算法通过将高维空间中的数据点映射到低维空间(通常是二维或三维空间)中,保留数据点之间的相对距离和分布,从而使得高维数据的结构更加清晰可见。
t-SNE 算法的主要思想是通过 t 分布来描述低维空间中的点之间的相对距离,而通过高斯分布来描述高维空间中的点之间的相对距离。t-SNE 算法通过优化 t 分布和高斯分布之间的 KL 散度来得到低维空间中的数据点位置。具体来说,算法首先随机初始化低维空间中的点的位置,然后通过梯度下降来最小化高维空间中数据点之间的相对距离与低维空间中数据点之间的相对距离之间的KL散度,从而得到最终的低维表示。
t-SNE 算法的流程如下:
1.计算高维空间中的相对距离矩阵;
2.通过高斯分布来描述高维空间中的点之间的相对距离;
3.计算低维空间中的相对距离矩阵;
4.通过 t 分布来描述低维空间中的点之间的相对距离;
5.通过梯度下降来最小化高维空间中数据点之间的相对距离与低维空间中数据点之间的相对距离之间的KL散度;
6.重复第 5 步直至满足收敛条件,得到最终的低维表示。
t-SNE 算法的应用
t-SNE 算法可以用于可视化高维数据,以便更好地理解数据之间的关系。下面的示例将展示如何使用 t-SNE 算法可视化手写数字数据集 MNIST 中的图像。
4、线性判别分析(LDA)
线性判别分析(Linear Discriminant Analysis, LDA) 也是一种常用的线性降维方法,它与 PCA 不同的是,LDA 考虑了样本的类别信息。LDA 试图在降维的过程中保留类别之间的差异,以找到更具有判别性的特征。因此,LDA 在分类问题中特别有用。
LDA 的思想可以用一句话概括,就是“投影后类内方差最小,类间方差最大”。通俗理解就是:将数据在低维度上进行投影,投影后希望每一种类别数据的投影点尽可能的接近,而不同类别的数据的类别中心之间的距离尽可能的大。
之所以称为线性判别分析,其实是因为其最早用在分类当中:判别分析是寻找一种“分类规则”,即利用变量的函数(判别函数)来描述(解释)两组或多组之间的区别。
5、奇异值分解(SVD)
在 2006 年,Netflix 曾经举办了一个奖金为 100 万美元的推荐系统算法比赛,最后的获奖者就使用了矩阵分解中的明星:奇异值分解(Singular-Value Decomposition,简称SVD)。SVD 被广泛应用在推荐系统、图像处理等领域,是一种数据降维的经典方法。
奇异值分解是将矩阵分解为奇异向量和奇异值。通过奇异值分解,我们会得到一些与特征分解相同类型的信息。然而,奇异值分解有更广泛的应用。每一个实数矩阵都有一个奇异值分解,但不一定都有特征分解(例如非方阵矩阵)。
6、局部线性嵌入(LLE)
局部线性嵌入(Locally linear embedding,LLE)是一种非线性降维算法,它能够使降维后的数据较好地保持原有 流形结构 。LLE 可以说是流形学习方法最经典的工作之一。很多后续的流形学习、降维方法都与 LLE 有密切联系。
LLE 是非常重要的降维方法。和传统的 PCA,LDA 等关注样本方差的降维方法相比,LLE 关注于降维时保持样本局部的线性特征,由于 LLE 在降维时保持了样本的局部特征,它广泛的用于图像图像识别,高维数据可视化等领域。
一个形象的流形降维过程如下图。我们有一块卷起来的布,我们希望将其展开到一个二维平面,我们希望展开后的布能够在局部保持布结构的特征,其实也就是将其展开的过程,就像两个人将其拉开一样。
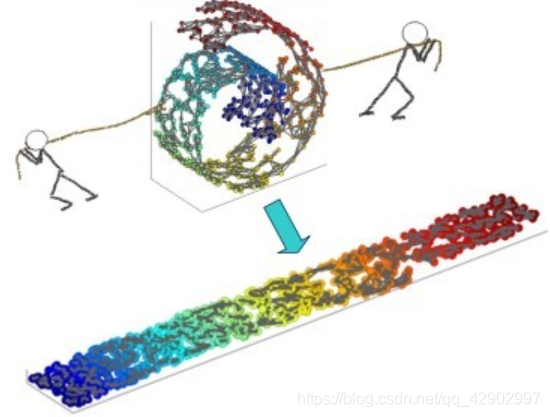
7、多维缩放(MDS)
多维缩放(Multiple Dimensional Scaling,简称 MDS)是一种经典的降维方法,要求原始空间中样本之间的距离在低维空间中得以保持。
多维缩放,即对一组对象之间的距离或差异的视觉表示。“对象”可以是颜色,面孔,地图坐标,各种真实存在的事物。除了将不同之处解释为图上的距离之外,MDS还可以作为高维数据的降维技术。简而言之。MDS 的主要目的是将这些差异保持在降维中。
MDS 算法思想很简单,一句话就是保持样本在原空间和低维空间的距离不变。
8、等度量映射(Isomap)
Isomap(等度量映射)是在 MDS 算法的基础上衍生出的一种非迭代的全局优化算法,它是一种等距映射算法,也就是说降维后的点,两两之间距离不变,这个距离是测地距离。
Isomap 方法是假设显示情况中非线性数据的分布位于内嵌欧式距离的流形体上,其中的关键在于数据点之间的距离用测地线距离来代替欧氏距离。
Isomap)的基本观点同 MDS 较为类似,即从高维数据中找到任意两个样本点之间的“测地距离”,通过映射实现在低维空间中“测地距离”近似保持不变。
与 MDS 不同的是,MDS 计算的是欧氏距离,而 Isomap 计算的是“测地距离”。
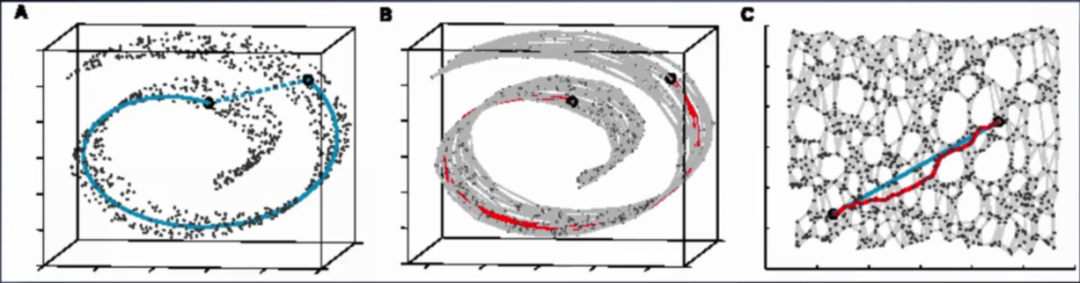
如上图,“测地距离”即A中沿曲实线的两点之间的距离,欧氏距离即如A中虚直线的两点之间的直线距离。B图即A的近邻图,C图即B图的低维映射结果,C图中红线为它的“测地距离”而蓝线则为欧氏距离。
很明显,Isomap中计算“测地距离”是非常重要的一步。如何计算“测地距离”呢?
我们可以利用流形在局部上与欧氏空间同胚这个性质,对每个点基于欧氏距离找出近邻点,然后建立一个近邻图。于是计算两点之间测地距离的问题就变成了计算近邻图上两点之间的最短路径问题。而计算最短路径可以使用 Dijkstra 算法或 Floyd 算法。得到任意两点的距离之后就可以通过 MDS 算法来获得样本点在低维空间中的坐标。



































