2016 年 3 月,一场机器人与围棋世界冠军、职业九段棋手李世石展开的围棋人机大战受到全球的高度关注。我们知道,最后的结果是 DeepMind 的机器人 AlphaGo 以 4 比 1 的总比分获胜。这是人工智能领域一个里程碑性的事件,也让「博弈」成为一个热门的 AI 研究方向。
AlphaGo 之后,DeepMind 又推出了赢得国际象棋的 AlphaZero、击败《星际争霸 II》的 AlphaStar 等等。使用搜索和学习的方法,AI 在许多完美信息博弈中表现出强大的性能,而使用博弈论推理和学习的方法在特定的不完美信息博弈中表现出强大的性能。
然而,大多数成功案例有一个重要的共同点:专注于单一博弈项目。例如,AlphaGo 不会下国际象棋,而 AlphaZero 虽然掌握了三种不同的完美信息博弈,但 AlphaZero 无法玩扑克牌,也不清楚能否扩展到不完美信息博弈。此外,现有研究往往会使用特定领域的知识和结构使 AI 实现强大的性能。
现在,来自 Google Deepmind 的研究团队提出了一种利用自我博弈学习、搜索和博弈论推理实现强大博弈性能的通用学习算法 ——Student of Games(SoG)。研究论文发表在《Science Advances》上。

论文地址:https://www.science.org/doi/full/10.1126/sciadv.adg3256
SoG 算法结合了引导式搜索(guided search)、自我对弈(self-play)学习和博弈论推理(game-theoretic reasoning)。实验结果表明,SoG 可以在大型完美和不完美信息博弈中表现出强大的性能,这是迈向任意环境真正通用算法的重要一步。
方法简介
SoG 模型可以在不同的游戏中自由发挥,并教会自己如何与自己的另一个版本进行对战,能够学习新策略并逐渐变得更有能力。虽然 AlphaZero 也可以适应完美信息博弈,但 SoG 可以适应完美和不完美信息博弈,从而具有更强的通用性。
SoG 采用成长树虚拟遗憾最小化(growing-tree counterfactual regret minimization,GT-CFR)算法。GT-CFR 算法是一种随时可以进行局部搜索,非均匀地构建子博弈,并将树扩展至最相关的未来状态,同时可以迭代地细化价值与策略。
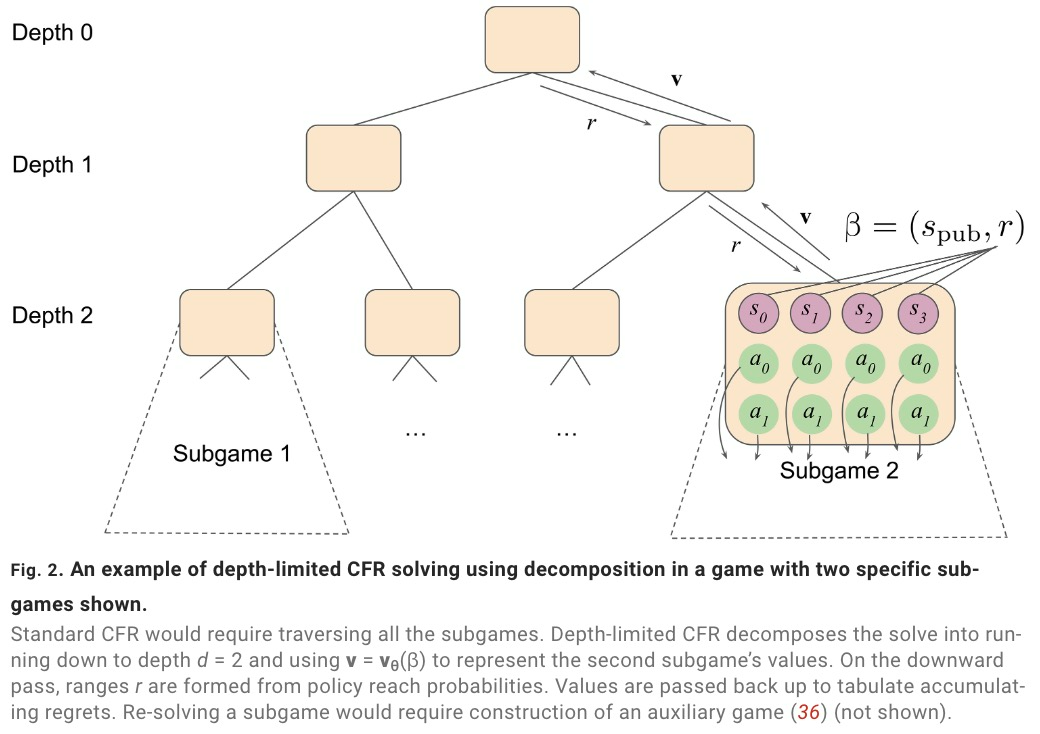
此外,SoG 还采用了有效的自我对弈:利用博弈结果和递归子搜索来训练价值与策略网络,并应用于之前搜索中出现过的情况。
SoG 算法通过声音自我对弈来训练智能体:每个玩家在面临决策时,使用配备虚拟价值与策略网络(Counterfactual Value-and-Policy Network,CVPN)的声音 GT-CFR 搜索来生成当前状态的策略,并根据该策略采取行动。
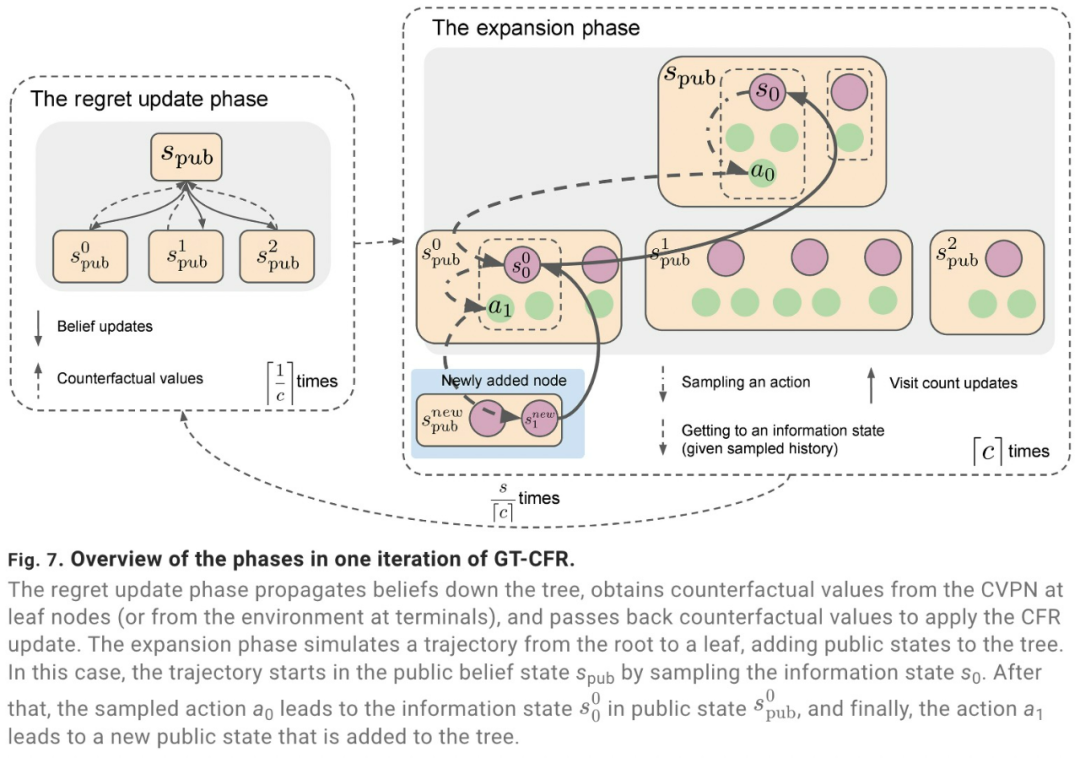
自我对弈过程会生成两种类型的训练数据,用于更新价值与策略网络,一种是搜索查询,一种是完整博弈轨迹。在实际应用中,自我对弈数据生成和训练是并行发生的:参与者生成自我对弈数据(并解决查询);训练者学习新网络并定期更新参与者。
实验结果
众所周知,传统搜索在不完美信息博弈中存在缺陷,并且评估集中在单一领域(如扑克牌),SoG 填补了这一空白。通过重新解决子博弈,SoG 保证可以找到近似纳什均衡,并且在小型博弈中保证可计算性。
具体来说,SoG 在四种不同的游戏中展示了强大的性能:两种完美信息博弈(国际象棋和围棋)和两种不完美信息博弈(扑克和 Scotland Yard)。值得注意的是,与扑克相比,Scotland Yard 的搜索范围和游戏长度要长得多,需要长期规划。
SoG 与 AlphaZero 一样,利用最少的领域知识,将搜索与自我对弈相结合。与 MCTS 不同,SoG 的搜索算法基于虚拟遗憾最小化,对完美和不完美信息博弈都是有效的。
下图展示了 SoG 在不同数量 GT-CFR 下的可利用性。
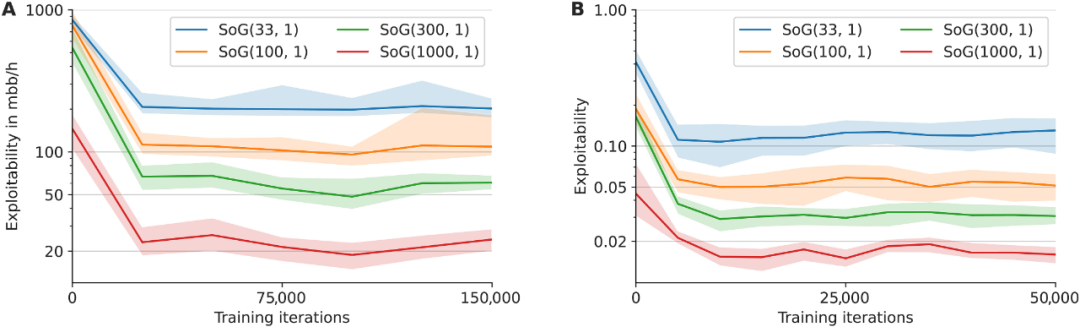
A 表为 Leduc 扑克,B 表为苏格兰场
下图展示了 SoG 随着神经网络评估次数的增加与 AlphaZero 可扩展性的比较,测量方式为相对 Elo 评分尺度。

A 表为国际象棋,B 表为围棋




































