数学,作为科学的基石,一直以来都是研究和创新的关键领域。
最近,普林斯顿大学等七家机构联合发布了一个专门用于数学的大语言模型LLEMMA,性能媲美谷歌Minerva 62B,并公开了其模型、数据集和代码,为数学研究带来了前所未有的机会和资源。

论文地址:https://arxiv.org/abs/2310.10631
数据集地址:https://huggingface.co/datasets/EleutherAI/proof-pile-2
项目地址:https://github.com/EleutherAI/math-lm
LLEMMA承袭了Code Llama的基础,在Proof-Pile-2上进行了预训练。
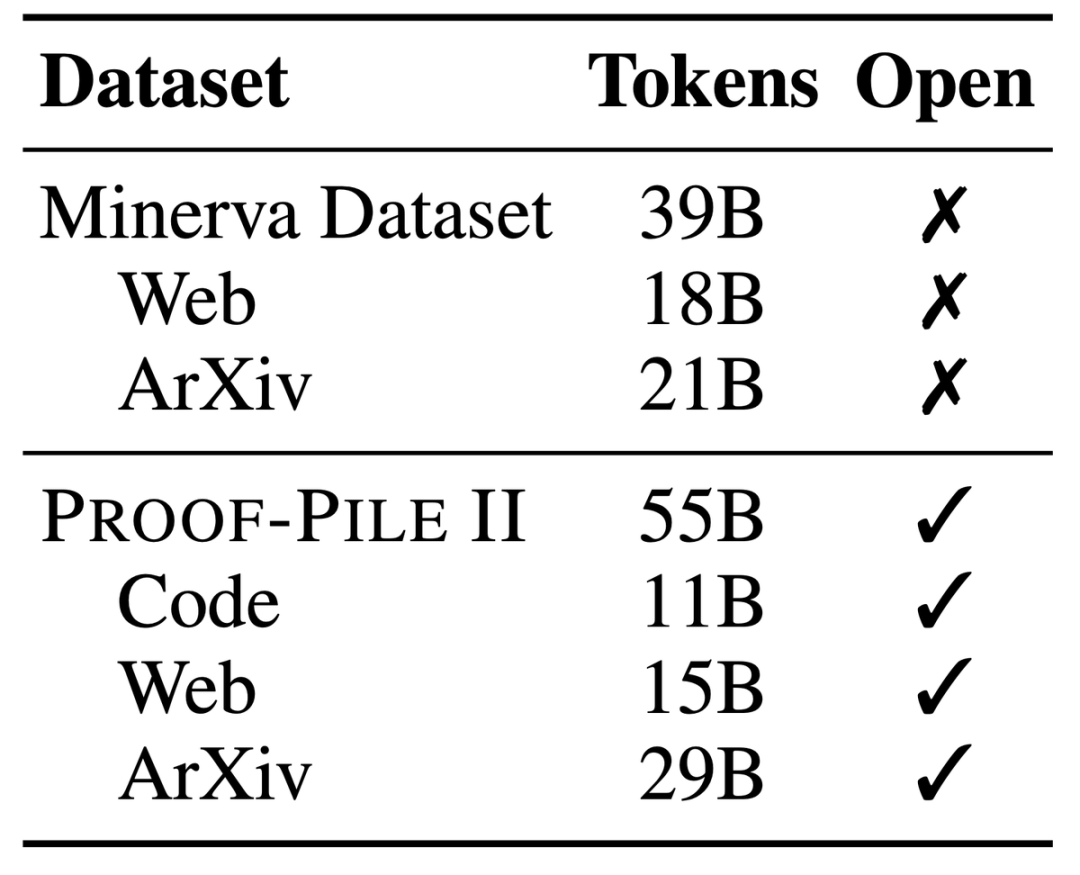
Proof-Pile-2,一个庞大的混合数据集,包含着550亿token的信息,其中包括科学论文、富含数学内容的网页数据以及数学代码。
这个数据集的一部分,Algebraic Stack,更是汇集了来自17种语言的11B数据集,覆盖了数值、符号和数学证明。
拥有7亿和34亿个参数,在MATH基准测试中表现卓越,超越了所有已知的开源基础模型。
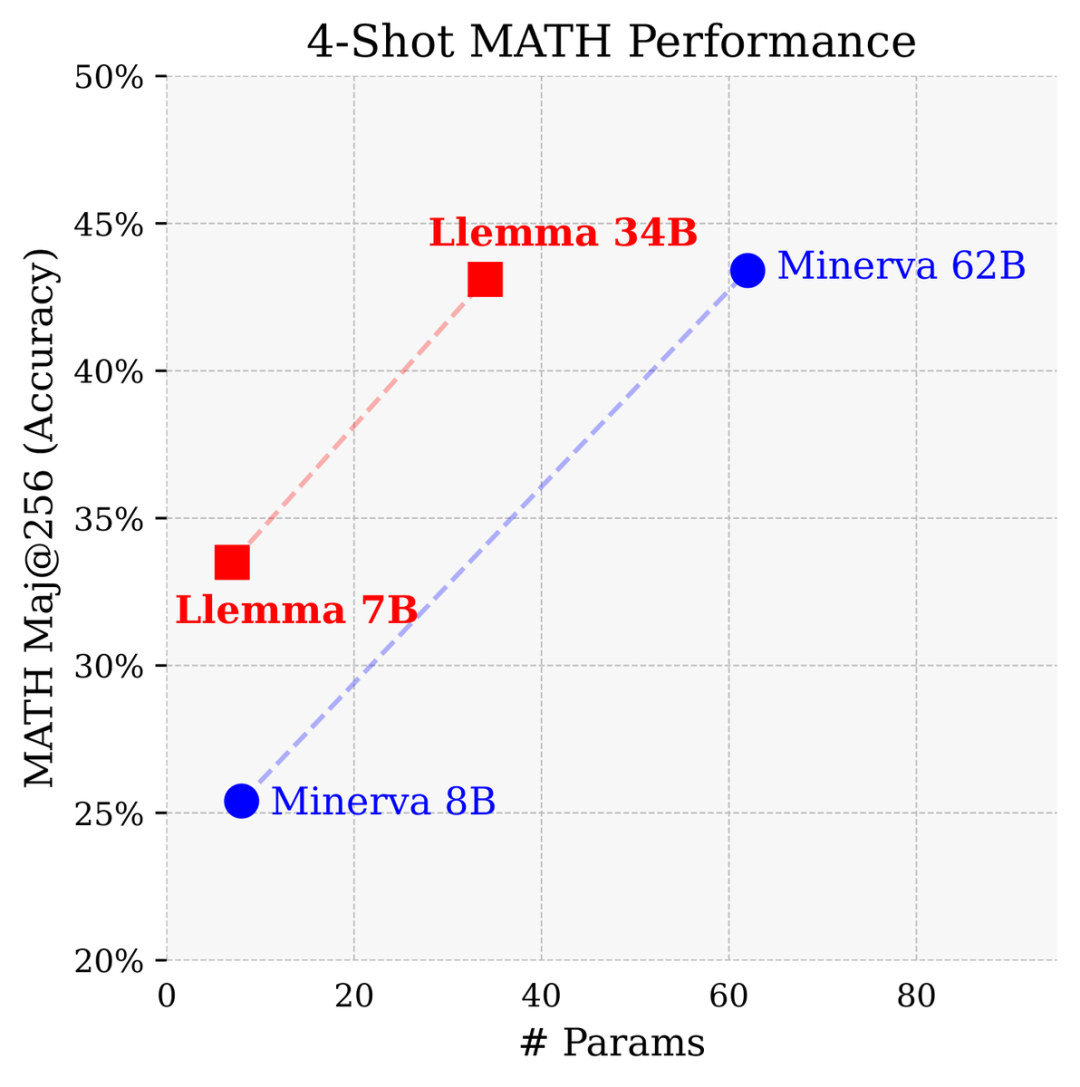
在与Google Research开发的专门用于数学的封闭模型相比,参数量只有Minerva 62B一半的条件下,Llemma 34B获得了几乎相同的性能。
Llemma在等参数基础上超越了Minerva的问题解决性能,通过应用计算工具和进行形式定理证明,为数学问题的解决提供了无限可能。
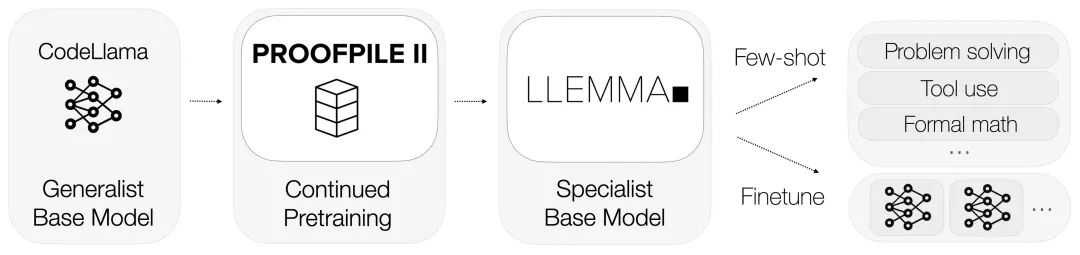
它能轻松使用Python解释器和形式定理证明器,进一步展示了其解决数学问题的能力。
由于Algebraic Stack中对形式证明数据的特别重视,Llemma是第一个展示出少样本定理证明能力的开放基础模型。

 图
图
研究人员还开放共享了LLEMMA的所有训练数据和代码。与以往的数学模型不同,LLEMMA是一个开源的、开放共享的模型,为整个科研社区敞开大门。
研究人员试图量化模型记忆的效果。令人惊讶的是,他们发现Llemma对于训练集中出现的问题并没有变得更加准确。由于代码和数据是开源的,研究人员鼓励其他人复制和扩展他们的分析。

训练数据和实验配置
LLEMMA是一个专门用于数学的大型语言模型,它在Code Llama的基础上继续在Proof-Pile-2上进行预训练,Proof-Pile-2是一个包含科学论文、含有数学内容的网页数据和数学代码的包含了550亿token的混合数据集。
其中的代码部分AlgebraicStack包含了17种语言源代码的11B数据集,涵盖数值、符号和形式数学,并已开源。
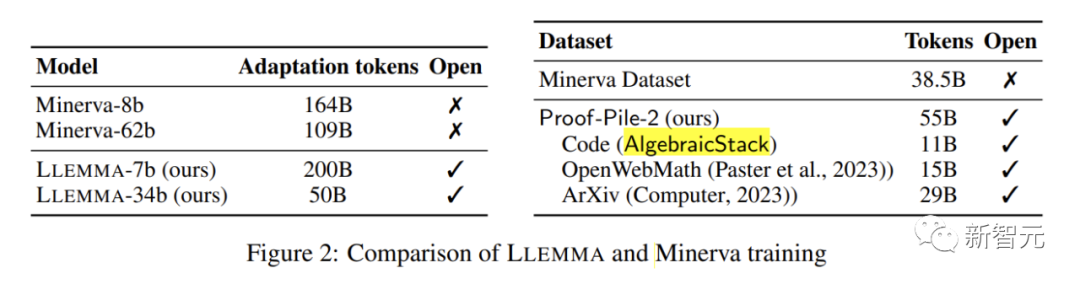
LLEMMA的每个模型均从Code Llama初始化。Code Llama模型是从Llama 2初始化的decoder-only的语言模型。
作者使用标准的自回归语言建模目标在Proof-Pile-2上继续训练Code Llama模型,对7B模型进行了200B token的训练,对34B模型进行了50B token的训练。
评估方法和实验结果
作者使用Proof-Pile-2对Code Llama进行继续预训练,并且在MATH和GSM8k等多个数学问题解决任务上对LLEMMA进行few-shot评估。
研究人员发现LLEMMA在这些任务上都有显著的提升,并且能够适应不同的问题类型和难度。
即便是在极高难度的数学题中,LLEMMA 34B也能够展示出与其他开放式基础模型相比更强大的数学能力。

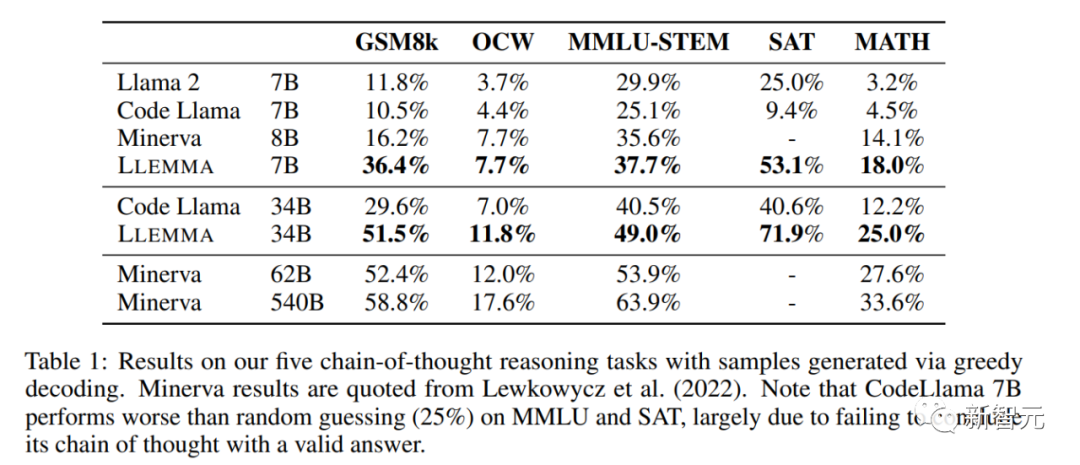
在数学基准测试上,LLEMMA在Proof-Pile-2上的持续预训练改善了五个数学基准测试的few-shot性能。
LLEMMA 34B在GSM8k上的改进比Code Llama高出20个百分点,在MATH上高出13个百分点。LLEMMA 7B也优于相似大小的专有的Minerva模型,这证明了在Proof-Pile-2上进行预训练能有效提高大模型的数学解题能力。
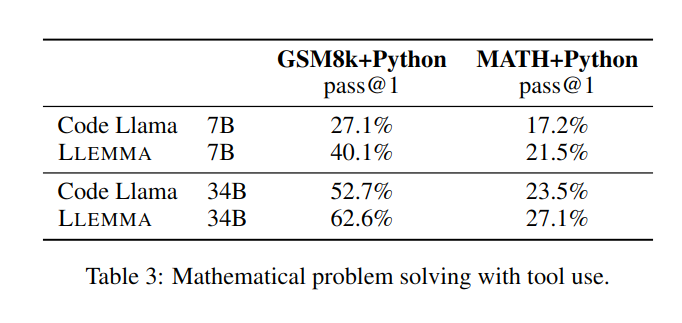
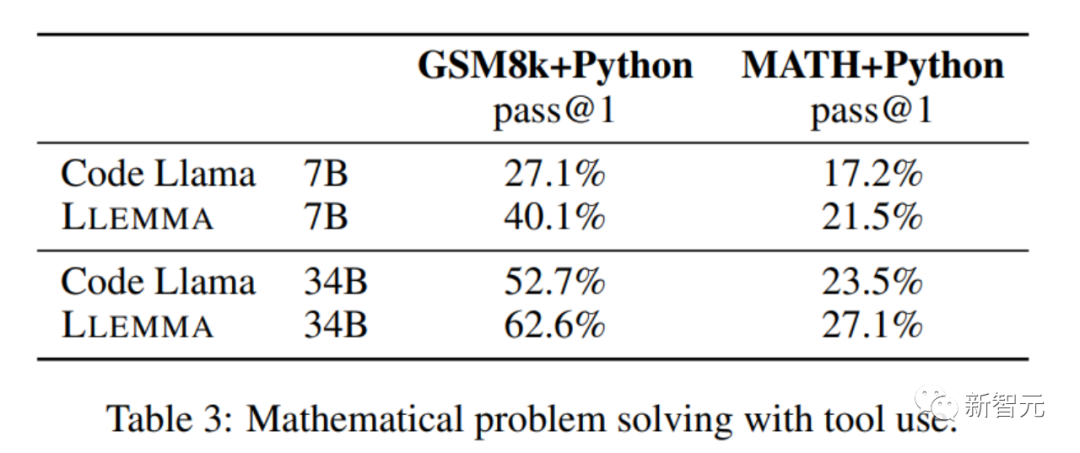
在利用计算工具,如Python等解决数学问题方面,在MATH+Python和GSM8k+Python任务上,LLEMMA都比Code Llama更胜一筹。
在使用工具的 MATH 和 GSM8k 数据集上,LLEMMA 的性能也高于不使用工具时的性能。
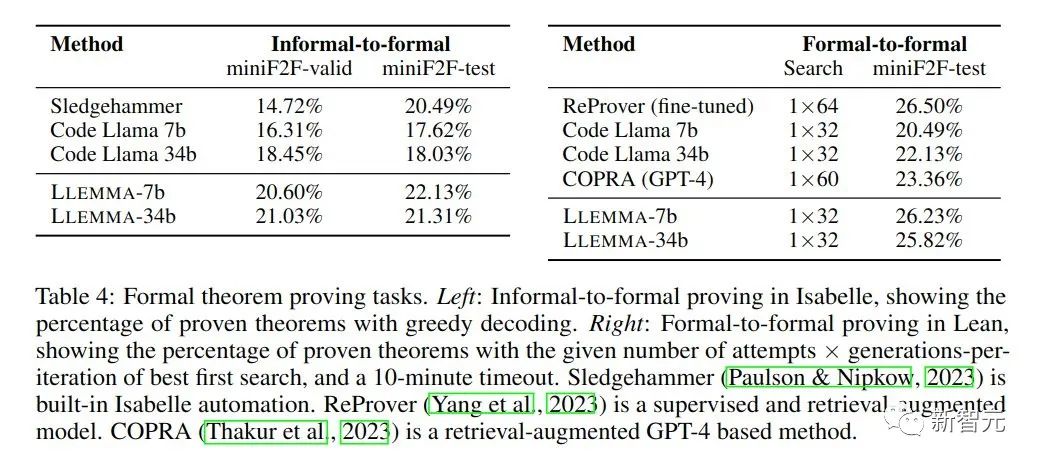
在数学证明任务上,LLEMMA也表现优异。
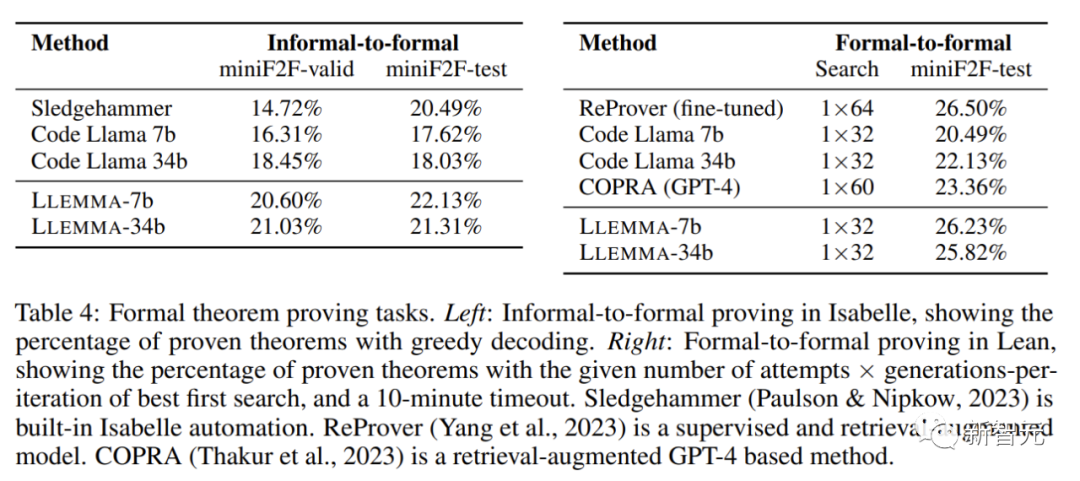
非正式到正式证明的任务目标是在给定一个正式陈述、一个非正式的LATEX陈述和一个非正式的LATEX证明的情况下,生成一个正式证明,然后通过证明助手进行验证。
正式到正式证明则是通过生成一系列证明步骤(策略)来证明一个正式陈述。结果表明,LLEMMA在Proof-Pile-2上的持续预训练改善了这两个正式定理证明任务的few-shot性能。
LLEMMA不仅拥有令人瞩目的性能、还开放了革命性的数据集、展现了惊人的问题解决能力。
开源共享的精神,标志着数学界进入了一个新的时代。数学的未来在这里,而我们每一个数学爱好者、研究者和教育者都将从中受益。
LLEMMA的出现为我们提供了前所未有的工具,让数学问题的解决变得更加高效和创新。
此外,开放共享的理念也将促进全球科研社区更加深入的合作,共同推动科学的进步。