Transformer 已经成功应用于自然语言处理、计算机视觉和时间序列预测等领域的各种学习任务。虽然取得了成功，但这些模型仍面临着严重的可扩展性限制，原因是对其注意力层的精确计算导致了二次（在序列长度上）运行时和内存复杂性。这对将 Transformer 模型扩展到更长的上下文长度带来了根本性的挑战。
业界已经探索了各种方法来解决二次时间注意力层的问题，其中一个值得注意的方向是近似注意力层中的中间矩阵。实现这一点的方法包括通过稀疏矩阵、低秩矩阵进行近似，或两者的结合。
然而，这些方法并不能为注意力输出矩阵的近似提供端到端的保证。这些方法旨在更快地逼近注意力的各个组成部分，但没有一种方法能提供完整点积注意力的端到端逼近。这些方法还不支持使用因果掩码，而因果掩码是现代 Transformer 架构的重要组成部分。最近的理论边界表明，在一般情况下，不可能在次二次时间内对注意力矩阵进行分项近似。
不过，最近一项名为 KDEFormer 的研究表明，在注意力矩阵项有界的假设条件下，它能在次二次时间内提供可证明的近似值。从理论上讲，KDEFormer 的运行时大约为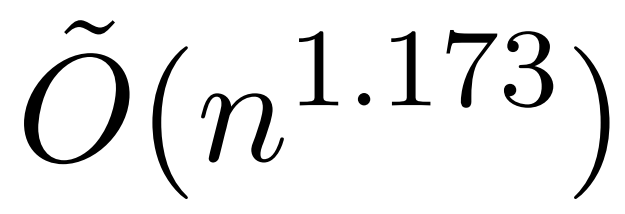
；它采用核密度估计 (kernel density estimation,KDE) 来近似列范数，允许计算对注意力矩阵的列进行采样的概率。然而，目前的 KDE 算法缺乏实际效率，即使在理论上，KDEFormer 的运行时与理论上可行的 O (n) 时间算法之间也有差距。在文中，作者证明了在同样的有界条目假设下，近线性时间的
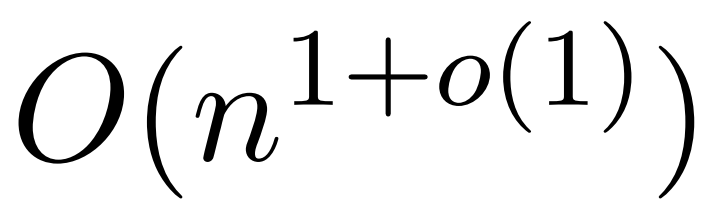算法是可能的。不过，他们的算法还涉及使用多项式方法来逼近 softmax，很可能不切实际。
而在本文中，来自耶鲁大学、谷歌研究院等机构的研究者提供了一种两全其美的算法，既实用高效，又是能实现最佳近线性时间保证。此外，该方法还支持因果掩码，这在以前的工作中是不可能实现的。
论文地址：https://arxiv.org/abs/2310.05869
本文提出一种名为「HyperAttention」近似注意力机制，以解决大型语言模型中使用的长上下文日益复杂带来的计算挑战。最近的工作表明，在最坏情况下，除非注意力矩阵的条目有界或矩阵的稳定秩较低，否则二次时间是必要的。
研究者引入了两个参数来衡量：（1）归一化注意力矩阵中的最大列范数，（2）检测和删除大条目后，非归一化注意力矩阵中的行范数的比例。他们使用这些细粒度参数来反映问题的难易程度。只要上述参数很小，即使矩阵具有无界条目或较大的稳定秩，也能够实现线性时间采样算法。
HyperAttention 的特点是模块化设计，可以轻松集成其他快速底层实现，特别是 FlashAttention。根据经验，使用 LSH 算法来识别大型条目，HyperAttention 优于现有方法，与 FlashAttention 等 SOTA 解决方案相比，速度有了显著提高。研究者在各种不同的长上下文长度数据集上验证了 HyperAttention 的性能。
例如，HyperAttention 使 ChatGLM2 在 32k 上下文长度上的推理时间快了 50%，而困惑度从 5.6 增加到 6.3。更大的上下文长度（例如 131k）和因果掩码情况下，HyperAttention 在单个注意力层上速度提升了 5 倍。
方法概览
点积注意涉及处理三个输入矩阵: Q (queries) 、K (key)、V (value)，大小均为 nxd，其中 n 是输入序列中的 token 数，d 是潜在表征的维度。这一过程的输出结果如下:
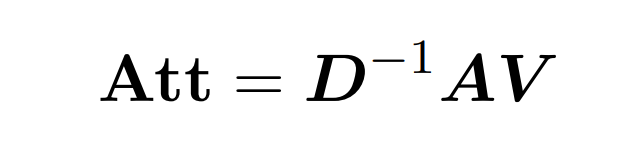
这里，矩阵 A := exp （QK^T) 被定义为 QK^T 的元素指数。D 是一个 n×n 对角矩阵，由 A 各行之和导出， 这里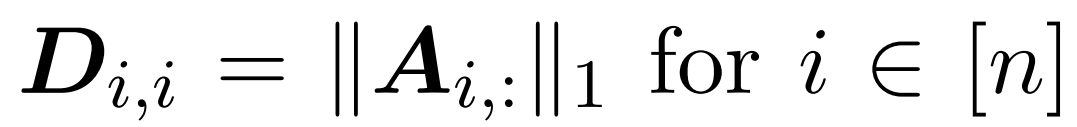
。在这种情况下，矩阵 A 被称为「注意力矩阵」，（D^-1 ) A 被称为「softmax 矩阵」。值得注意的是，直接计算注意力矩阵 A 需要 Θ（n²d）运算，而存储它需要消耗 Θ（n²）内存。因此，直接计算 Att 需要 Ω（n²d）的运行时和 Ω（n²）的内存。
研究者目标是高效地近似输出矩阵 Att，同时保留其频谱特性。他们的策略包括为对角缩放矩阵 D 设计一个近线性时间的高效估计器。此外，他们通过子采样快速逼近 softmax 矩阵 D^-1A 的矩阵乘积。更具体地说，他们的目标是找到一个具有有限行数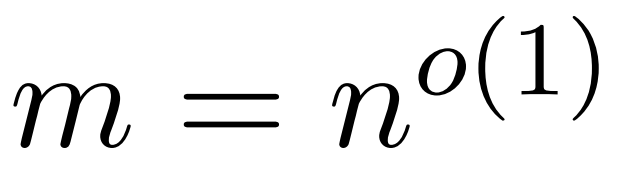
的采样矩阵
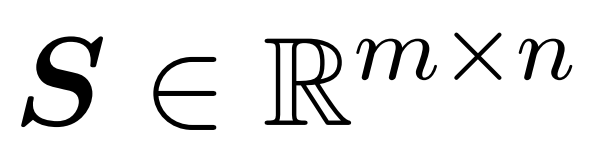以及一个对角矩阵
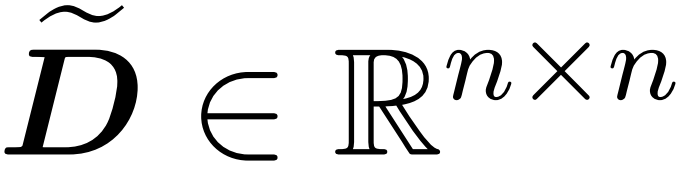，从而满足误差的算子规范的以下约束:
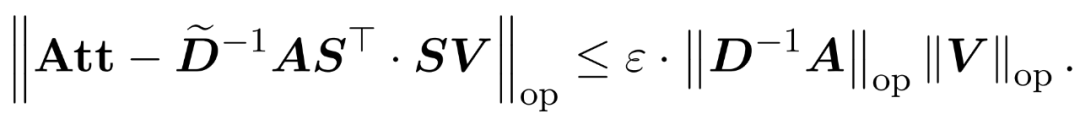
研究者表明，通过基于 V 的行规范定义采样矩阵 S，可以高效解决公式 (1) 中注意力近似问题的矩阵乘法部分。更具挑战性的问题是：如何获得对角矩阵 D 的可靠近似值。在最近的成果中，Zandieh 有效地利用了快速 KDE 求解器来获得 D 的高质量近似值。研究者简化了 KDEformer 程序，并证明均匀采样足以实现所需的频谱保证，而无需基于内核密度的重要性采样。这一重大简化使他们开发出了一种实用的、可证明的线性时间算法。
与之前的研究不同，本文方法并不需要有界条目或有界稳定秩。此外，即使注意力矩阵中的条目或稳定秩很大，为分析时间复杂性而引入的细粒度参数仍可能很小。
因此，HyperAttention 的速度有了显著提高，在序列长度为 n= 131k 时，前向和后向传播速度提高了 50 倍以上。在处理因果掩码时，该方法仍能大幅提高 5 倍的速度。此外，当该方法应用于预训练的 LLM (如 chatqlm2-6b-32k ）并在长语境基准数据集 LongBench 上进行评估时，即使不需要微调，也能保持与原始模型接近的性能水平。研究者还对特定任务进行了评估，他们发现总结和代码完成任务比问题解答任务对近似注意力层的影响更大。
算法
为了在近似 Att 时获得频谱保证，本文第一步是对矩阵 D 的对角线项进行 1 ± ε 近似。随后，根据 V 的平方行ℓ₂-norms，通过采样逼近 （D^-1）A 和 V 之间的矩阵乘积。
近似 D 的过程包括两个步骤。首先，使用植根于 Hamming 排序 LSH 的算法来识别注意力矩阵中的主要条目，如定义 1 所示。第二步是随机选择一小部分 K。本文将证明，在矩阵 A 和 D 的某些温和假设条件下，这种简单的方法可以建立估计矩阵的频谱边界。研究者的目标是找到一个足够精确的近似矩阵 D，满足:
本文的假设是，softmax 矩阵的列范数呈现出相对均匀的分布。更准确地说，研究者假设对于任意 i ∈ [n] t 存在某个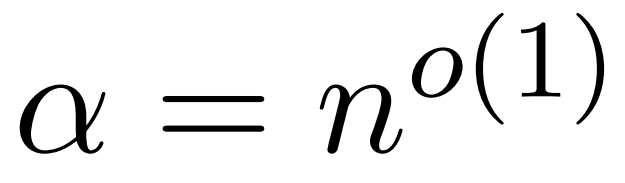
，使得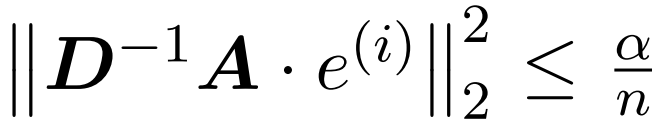
。
算法的第一步是使用 Hamming 排序 LSH (sortLSH) 将键和查询散列到大小均匀的桶中，从而识别注意力矩阵 A 中的大型条目。算法 1 详细介绍了这一过程，图 1 直观地说明了这一过程。
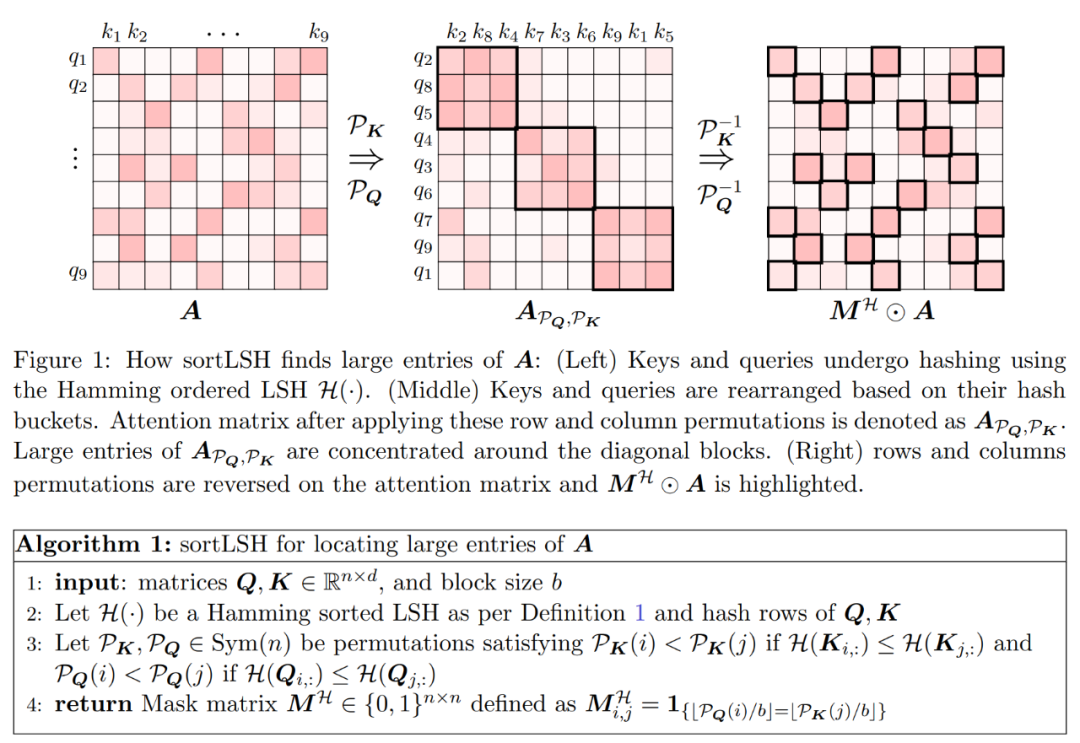
算法 1 返回一个稀疏掩码，旨在隔离注意力矩阵的主要条目。给定该掩码后，研究员在算法 2 中计算矩阵 D 的近似值，该近似值满足公式 (2) 中的频谱保证。该算法通过将掩码对应的注意力值与注意力矩阵中随机选择的列子集相结合来实现。本文算法用途广泛，可以有效地使用预定义的掩码，该掩码指定了注意力矩阵中主要条目的位置。本算法提供的主要保证在定理 1 中给出。
整合近似对角线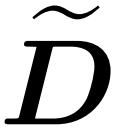
和近似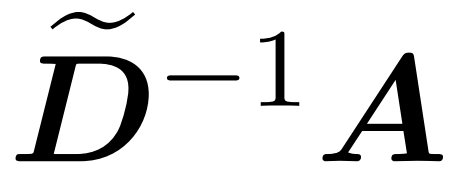
与值矩阵 V 之间矩阵乘积的子程序。因此，研究者引入了 HyperAttention，这是一种高效算法，可以在近似线性时间内近似公式（1）中具有频谱保证的注意力机制。算法 3 将定义注意力矩阵中主导条目的位置的掩码 MH 作为输入。这个掩码可以使用 sortLSH 算法（算法 1）生成，也可以是一个预定义的掩码，类似于 [7] 中的方法。研究者假定大条目掩码 M^H 在设计上是稀疏的，而且其非零条目数是有界的
。
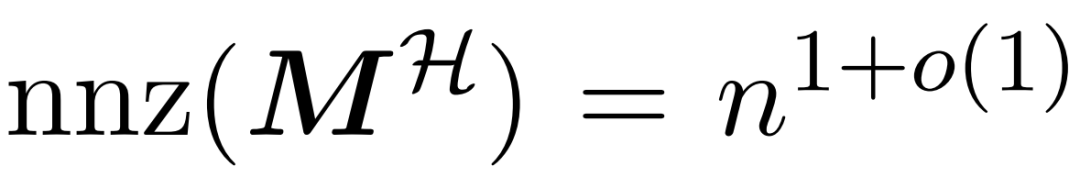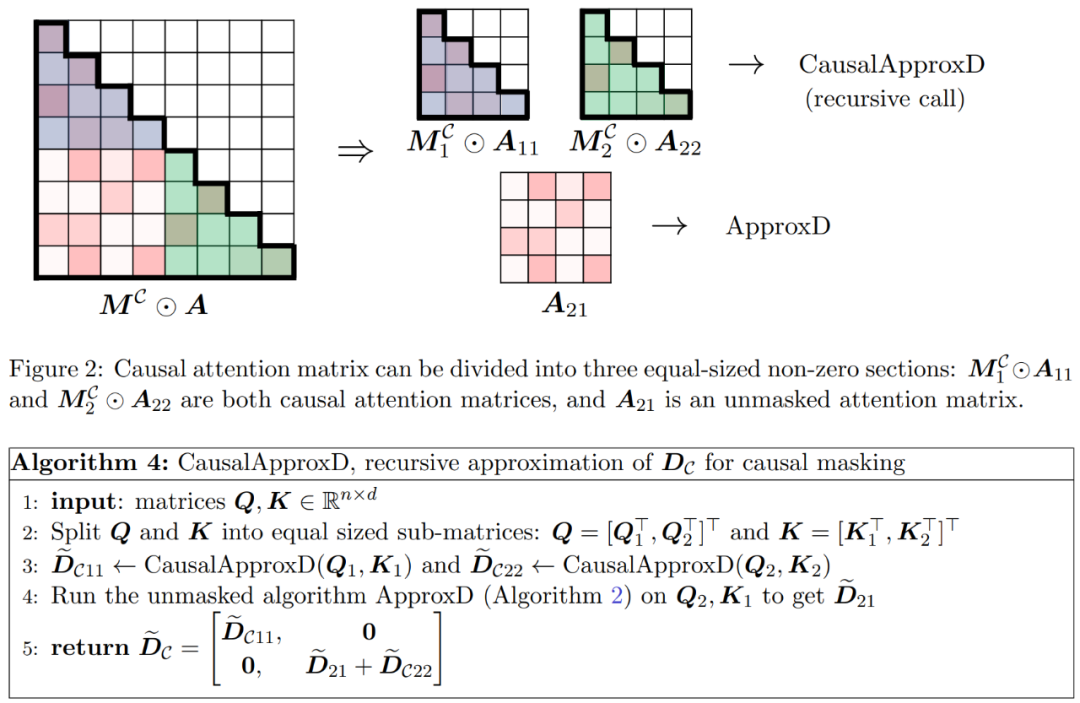
如图 2 所示，本文方法基于一个重要的观察结果。屏蔽注意力 M^C⊙A 可以分解成三个非零矩阵，每个矩阵的大小是原始注意力矩阵的一半。完全位于对角线下方的 A_21 块是未屏蔽注意力。因此，我们可以使用算法 2 近似计算其行和。
图 2 中显示的两个对角线区块
和
是因果注意力，其大小只有原来的一半。为了处理这些因果关系，研究者采用递归方法，将它们进一步分割成更小的区块，并重复这一过程。算法 4 中给出了这一过程的伪代码。
实验及结果
研究者通过扩展现有大语言模型来处理 long range 序列，进而对算法进行基准测试。所有实验都在单个 40GB 的 A100 GPU 上运行，并用 FlashAttention 2 来进行精确的注意力计算。
Monkey Patching 自注意力
研究者首先在两个预训练 LLM 上评估 HyperAttention，选择了实际应用中广泛使用的具有不同架构的两个模型：chatglm2-6b-32k 和 phi-1.5。
在操作中，他们通过替换为 HyperAttention 来 patch 最终的ℓ注意力层，其中ℓ的数量可以从 0 到每个 LLM 中所有注意力层的总数不等。请注意，两个模型中的注意力都需要因果掩码，并且递归地应用算法 4 直到输入序列长度 n 小于 4,096。对于所有序列长度，研究者将 bucket 大小 b 和采样列数 m 均设置为 256。他们从困惑度和加速度两个方面评估了这类 monkey patched 模型的性能。
同时研究者使用了一个长上下文基准数据集的集合 LongBench，它包含了 6 个不同的任务，即单 / 多文档问答、摘要、小样本学习、合成任务和代码补全。他们选择了编码序列长度大于 32,768 的数据集的子集，并且如果长度超过 32,768，则进行剪枝。接着计算每个模型的困惑度，即下一个 token 预测的损失。为了突出长序列的可扩展性，研究者还计算所有注意力层的总加速，无论是由 HyperAttention 还是 FlashAttention 执行。
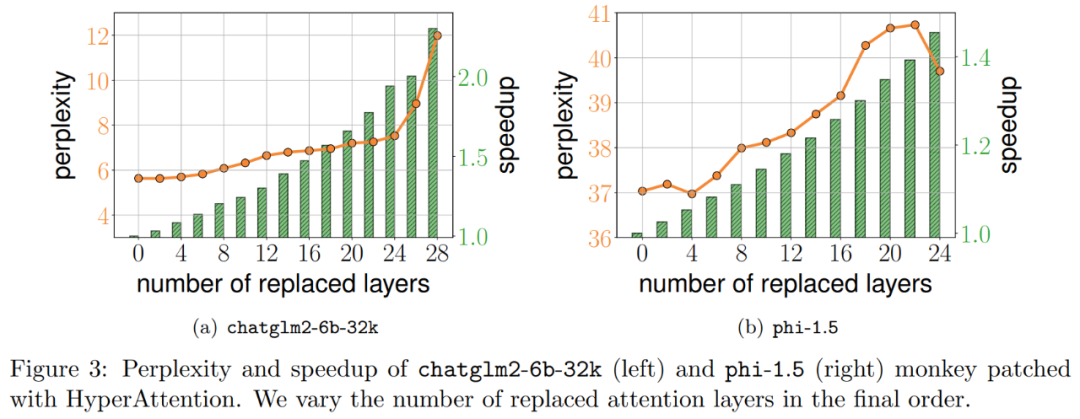
结果如下图 3 所示，即使经过 HyperAttention 的 monkey patch，chatglm2-6b-32k 仍显示出合理的困惑度。例如替换 20 层后，困惑度大约增加了 1，并在达到 24 层之前继续缓慢增加。注意力层的运行时提升了大约 50%。如果所有层都被替换，则困惑度上升到 12，运行速度提升 2.3。phi-1.5 模型也表现出了类似的情况，但随着 HyperAttention 数量的增加，困惑度会线性增长。
此外，研究者评估了 LongBench 数据集上 monkey patched chatglm2-6b-32k 的性能，并计算单 / 多文档问答、摘要、小样本学习、合成任务和代码补全等各自任务上的评估分数。结果如下表 1 所示。
虽然替换 HyperAttention 通常会导致性能下降，但他们观察到它的影响会基于手头任务发生变化。例如，摘要和代码补全相对于其他任务具有最强的稳健性。
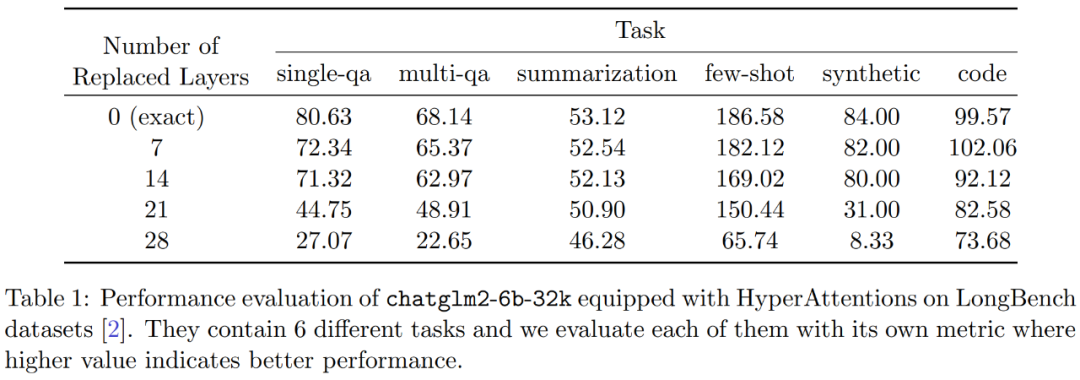
显著的一点是，当半数注意力层（即 14 层）被 patch 之后，研究者证实了大多数任务的性能下降幅度不会超过 13%。尤其是摘要任务，其性能几乎保持不变，表明该任务对注意力机制中的部分修改具有最强的稳健性。当 n=32k 时，注意力层的计算速度提升了 1.5 倍。
单个自注意力层
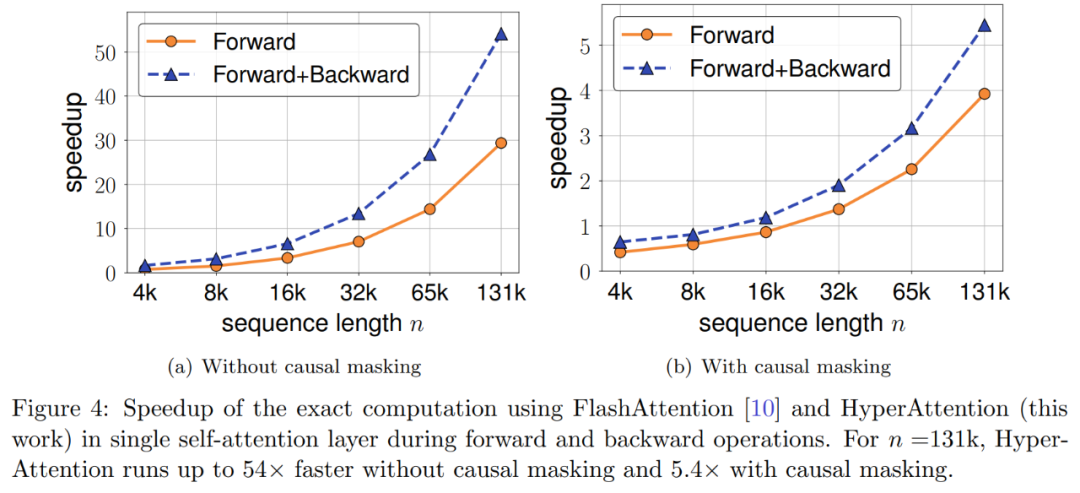
研究者进一步探索了序列长度从 4,096 到 131,072 不等时，HyperAttention 的加速度。他们测量了当使用 FlashAttention 计算或通过 HyperAttention 加速时，前向和前向 + 后向操作的挂钟时间。此外还测量了有或没有因果掩码时的挂钟时间。所有输入 Q、K 和 V 的长度相同，维数固定为 d = 64，注意力头数量为 12。
他们在 HyperAttention 中选择与前文相同的参数。如下图 4 所示，HyperAttention 在没有应用因果掩码时速度提升 54 倍，用了之后速度提升 5.4。尽管因果掩码和非掩码的时间困惑度相同，但因果掩码的实际算法（算法 1）需要额外的操作，例如分区 Q、K 和 V、合并注意力输出，从而导致实际运行时增加。当序列长度 n 增加时，加速度会更高。
研究者认为，不仅对于推理，而且对于训练或微调 LLM 以适应更长的序列，这些结果为扩展自注意力打开了大门。
