算法是编码面试中最常见的主题之一。为了在面试中获得优势,非常熟悉顶级算法及其实现非常重要。
在次此篇文章中,我们将探索图算法。我们将从图论和图算法的介绍开始。接下来,我们将学习如何实现图。
今天,我们将学习:
- 什么是图算法?
- 图的属性
- 如何在代码中表示图形
- 如何实现广度优先遍历
- 如何实现深度优先遍历
- 如何去除边缘
什么是图算法?
算法是使用明确定义或最佳步骤数解决问题的数学过程。它只是用于完成特定工作的基本技术。
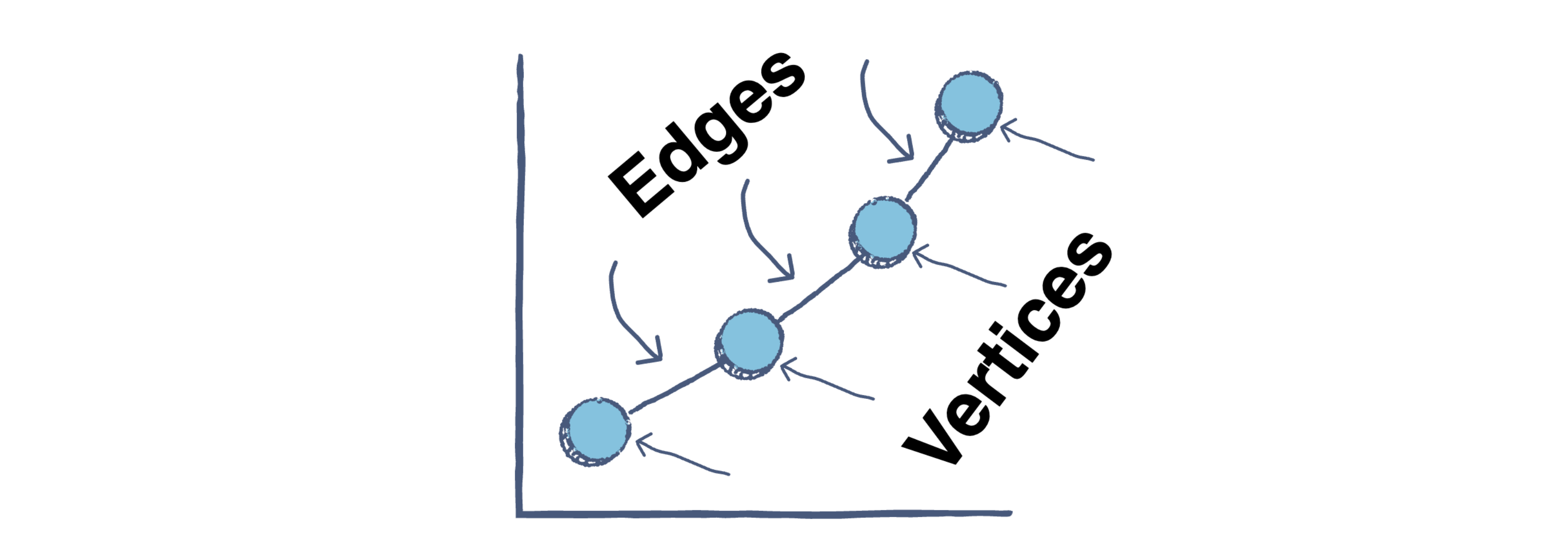
图是一种抽象符号,用于表示所有对象对之间的连接。图是广泛使用的数学结构,由两个基本组成部分可视化:节点和边。
图算法用于解决将图表示为网络的问题,例如航空公司航班、互联网如何连接或微信、QQ、微博上的社交网络连接。它们在NLP和机器学习中也很流行,用于形成网络。
一些顶级的图形算法包括:
- 实现广度优先遍历
- 实现深度优先遍历
- 计算图级别中的节点数
- 查找两个节点之间的所有路径
- 查找图的所有连通分量
- Dijkstra 算法在图数据中查找最短路径
- 移除边缘
虽然图是离散数学不可或缺的一部分,但它们在计算机科学和编程中也有实际用途,包括以下内容:
- 计算机程序中以图形表示的调用者-被调用者关系
- 网站的链接结构可以用有向图来表示
- 神经网络
图的属性
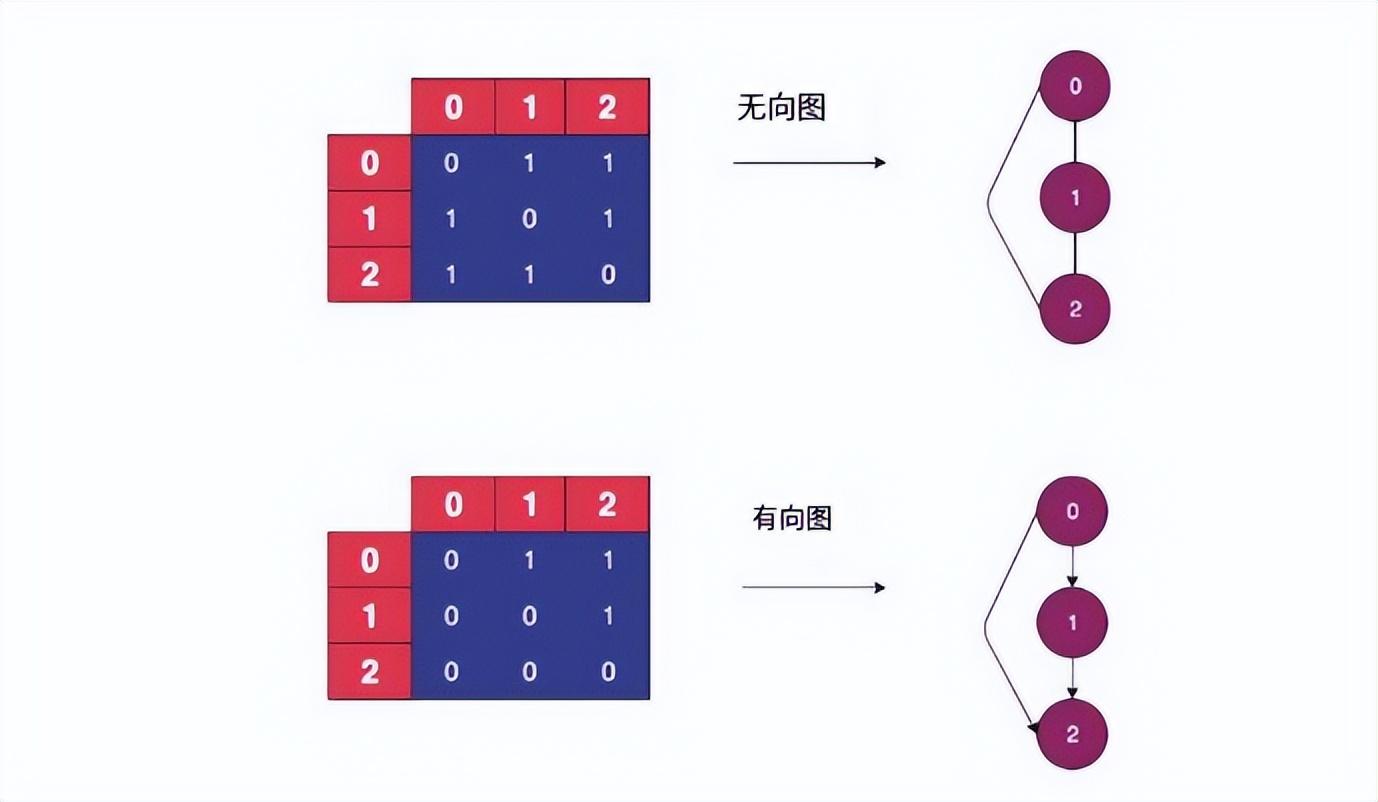
由 G 表示的图由一组顶点 (V)或在边 (E)处链接的节点表示。边的数量取决于顶点。边缘可以是有向的或无向的。
在有向图中,节点沿一个方向链接。这里的边显示了一种单向关系。
在无向图中,边是双向的,显示出双向关系。
示例:无向图的一个很好的用例是微信好友建议算法。用户(节点)有一个边缘运行到朋友 A(另一个节点),而朋友 A 又连接(或有一个边缘运行)到朋友 B。然后将朋友 B 推荐给用户。
还有许多其他复杂类型的图属于不同的子集。例如,当每个顶点都可以从其他每个顶点到达时,有向图就具有强连通分量。
顶点
顶点是多条线相交的点。它也称为节点。
边缘
边是一个数学术语,用于表示连接两个顶点的线。许多边可以由单个顶点形成。然而,没有顶点,就无法形成边。每条边必须有一个起始和结束顶点。
路径
图中的路径G=( V ,E )是顶点 v1, v2, …, vk 的序列,其属性是之间有边 vi 和 vi +1。我们说路径从v1到vk 。
序列 6,4,5,1,26,4,5,1,2 定义从节点 6 到节点 2 的路径。
类似地,可以通过遍历图的边来创建其他路径。如果路径的顶点全部不同,则路径很简单。
行走
行走是路径,但它们不需要一系列不同的顶点。
连通图
如果对于每对顶点,则图是连通的v和v,有一条路径从v到v。
循环
循环是一条路径 v1, v2, …, vk,满足以下条件:
- k>2k>2k>2k _>2
- 首先k-1顶点都不同
- v1=vk
树
树是不包含环的连通图。
环形
在图中,如果从顶点到自身绘制一条边,则称为环。在图中,V 是一个顶点,其边 (V, V) 形成一个环。
如何在代码中表示图形
在我们继续使用图算法解决问题之前,首先了解如何在代码中表示图非常重要。图可以表示为邻接矩阵或邻接列表。
邻接矩阵
邻接矩阵是由图顶点标记的方阵,用于表示有限图。矩阵的条目指示顶点对在图中是否相邻。
在邻接矩阵表示中,需要迭代所有节点来识别节点的邻居。
a b c d e
a 1 1 - - -
b - - 1 - -
c - - - 1 -
d - 1 1 - -邻接表
邻接表用于表示有限图。邻接列表表示允许轻松地遍历节点的邻居。列表中的每个索引代表顶点,与该索引链接的每个节点代表其相邻顶点。
1 a -> { a b }
2 b -> { c }
3 c -> { d }
4 d -> { b c }对于下面的基图类,我们将使用邻接列表实现,因为它对于本文后面的算法解决方案执行得更快。
图类(Graph Class)
我们的图实现的要求相当简单。我们需要两个数据成员:图中顶点的总数和存储相邻顶点的列表。我们还需要一种添加边或一组边的方法。
class AdjNode:
"""
表示节点邻接表的 类
"""
def __init__(self, data):
"""
构造函数
:参数数据 : 顶点
"""
self.vertex = data
self.next = None
class Graph:
"""
图类 ADT
"""
def __init__(self, vertices):
"""
构造函数
:param vertices : 图中的总顶点数
"""
self.V = vertices
self.graph = [None] * self.V
# 在无向图中添加边的函数
def add_edge(self, source, destination):
"""
添加边缘
:param source: 源顶点
:param destination: 目标顶点
"""
# 将节点添加到源节点
node = AdjNode(destination)
node.next = self.graph[source]
self.graph[source] = node
# 如果无向图,将源节点添加到目标节点
# 故意注释这一行,方便理解
#node = AdjNode(source)
#node.next = self.graph[destination]
#self.graph[destination] = node
def print_graph(self):
"""
打印图标的函数
"""
for i in range(self.V):
print("Adjacency list of vertex {}\n head".format(i), end="")
temp = self.graph[i]
while temp:
print(" -> {}".format(temp.vertex), end="")
temp = temp.next
print(" \n")
# 主程序
if __name__ == "__main__":
V = 5 # 顶点总数
g = Graph(V)
g.add_edge(0, 1)
g.add_edge(0, 4)
g.add_edge(1, 2)
g.add_edge(1, 3)
g.add_edge(1, 4)
g.add_edge(2, 3)
g.add_edge(3, 4)
g.print_graph()在上面的示例中,我们看到了Python graph class。我们已经奠定了图形类的基础。变量 V 包含一个整数,指定顶点总数。下面示例的代码都会用到这个类。
如何实现广度优先遍历
给定一个表示为邻接列表和起始顶点的图,代码应该输出一个字符串,其中包含以正确的遍历顺序列出的图的顶点。当从起始顶点遍历图形时,将首先打印每个节点的右子节点,然后是左子节点。
为了解决这个问题,前面已经实现了 Graph 类。
输入:表示为邻接列表和起始顶点的图。
输出:一个字符串,其中包含以正确的遍历顺序列出的图的顶点。

示例输出:
result = "02143"
or
result = "01234"在开始实施之前,先看一下并设计一个分步算法。首先尝试自己解决。如果遇到困难,可以随时参考解决方案部分提供的解决方案。
bfs:
def bfs(graph, source):
"""
打印图的 BFS 的函数
:param graph: 图表
:param source: 起始顶点
:return:
"""
# 写你的代码
pass解决方案
bfs:
def bfs(my_graph, source):
"""
打印图的 BFS 函数
:param graph: 图表
:param source: 起始顶点
:return:
"""
# 将所有的顶点标识为未访问过
visited = [False] * (len(my_graph.graph))
# 创建 BFS 队列
queue = []
# 结果字符串
result = ""
# 将源节点表示为 访问过并将其排入队列
queue.append(source)
visited[source] = True
while queue:
# 经一个顶点重队列中取出
# 排队并打印
source = queue.pop(0)
result += str(source)
# 取出相邻的顶点
# 出对的顶点源,
#如果一个相邻的还没有访问过,那么标记一下
# 访问过并将其排入队列
while my_graph.graph[source] is not None:
data = my_graph.graph[source].vertex
if not visited[data]:
queue.append(data)
visited[data] = True
my_graph.graph[source] = my_graph.graph[source].next
return result
# 主要测试上面的程序
if __name__ == "__main__":
V = 5
g = Graph(V)
g.add_edge(0, 1)
g.add_edge(0, 2)
g.add_edge(1, 3)
g.add_edge(1, 4)
print(bfs(g, 0))我们从选定的节点开始,逐层遍历图。探索所有邻居节点。然后,我们进入下一个级别。我们水平遍历图表,也就是每一层。
图表可能包含循环。为了避免再次处理同一节点,我们可以使用布尔数组来标记访问过的数组。可以使用队列来存储节点并将其标记为已访问。队列应遵循先进先出(FIFO)排队方法。
如何实现深度优先遍历
在这个问题中,你必须实现深度优先遍历。为了解决这个问题,之前实现的图类已经提供了。
输入:表示为邻接列表和起始顶点的图。
输出:一个字符串,其中包含以正确的遍历顺序列出的图的顶点。

示例输出:
result = "01342"
or
result = "02143"在开始实施之前,先看一下并设计一个分步算法。首先尝试自己解决。如果遇到困难,可以随时参考解决方案部分提供的解决方案。
dfs:
def dfs(graph, source):
"""
打印图的 DFS 的函数
:param graph: 图表
:param source: 起始顶点
:return:
"""
# 在这里写下你的代码!
pass解决方案
dfs:
def dfs(my_graph, source):
"""
打印图的DFS的函数
:param graph: 图表
:param source: 起始顶点
:return: 以字符串形式返回遍历结果
"""
# 将所有顶点标记为未访问过
visited = [False] * (len(my_graph.graph))
# 创建 DFS 堆栈
stack = []
# 结果字符串
result = ""
# 拼接字符
stack.append(source)
while stack:
# 从堆栈中弹出一个顶点
source = stack.pop()
if not visited[source]:
result += str(source)
visited[source] = True
# 获取弹出顶点源的所有相邻顶点
# 如果相邻的未必访问过,则将其压入
while my_graph.graph[source] is not None:
data = my_graph.graph[source].vertex
if not visited[data]:
stack.append(data)
my_graph.graph[source] = my_graph.graph[source].next
return result
# 主程序运行
if __name__ == "__main__":
V = 5
g = Graph(V)
g.add_edge(0, 1)
g.add_edge(0, 2)
g.add_edge(1, 3)
g.add_edge(1, 4)
print(dfs(g, 0))深度优先图算法利用了回溯的思想。这里的“回溯”是指只要当前路径上没有更多的节点,就向前移动,然后在同一条路径上向后移动,寻找要遍历的节点。
如何去除边缘
在此问题中,必须实现remove_edge以源和目标作为参数的函数。如果两者之间存在边,则应将其删除。
输入:图形、源(整数)和目标(整数)。
输出:对图进行 BFS 遍历,并删除源和目标之间的边。
首先,在开始实施之前仔细研究这个问题并设计一个分步算法。
remove_edge:
def remove_edge(graph, source, destination):
"""
删除边缘函数
:param graph: 图表
:param source: 源顶点
:param destination: 目标顶点
"""
# 写代码
pass解决方案
如果熟悉的话,这个解决方案与链表中的删除非常相似。
我们的顶点存储在一个链接列表中。首先,我们访问source链表。如果源链表的头节点持有要删除的键,我们将头向前移动一步并返回图。
如果要删除的键位于链表的中间,我们会跟踪前一个节点,并在目的地遇到时将前一个节点与下一个节点连接起来。
总结
图算法是用于解决图(Graph)数据结构中的各种问题的算法,对广度优先和深度优先做了一些示例,还有注释,我们可以私下练习一下。
图算法能够帮助我们理解和处理复杂的关系型数据,并在实际应用中提供解决方案。